Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots

M Bagheri Harouni

Quantum Optics Group,Department of Physics,University of Isfahan,Hezar Jerib St.,Isfahan 81764-73441,Iran

Keywords:quantum speed limit time,quantum entanglement,open quantum systems,spin–orbit effects

1.Introduction

Quantum speed limit time(QSLT)is an important concept in quantum dynamics which determines the speedup and slowdown of a quantum system.It is also an important concept in the quantum control field.The minimum time required to transfer a quantum state into a separated and distanced desired final state is known as the QSLT.Thus,via this quantity one can determine how fast a quantum system evolves.In quantum information processing,an elementary step of a computation process is transfer of a state to an orthogonal one.[1]Therefore,the concept of QSLT would possess some crucial roles in quantum technologies such as quantum computation[2]and optimal control theory.[3]

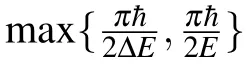
However,realistic physical systems,quantum systems are in interaction with their surrounding environment.Therefore,the concept of QSLT has been extended to open quantum systems.[9–11]Also,the influences of leakage and decoherence on the QSLT were studied.[12]In addition to the notion of QSLT in open quantum systems,QSL is introduced as a measure of asymmetry in quantum systems.[13]In the present contribution,using the introduced approach of Ref.[11],the QSLT in a two-spin system under non-Markovian dynamics is investigated.

In addition to the above-mentioned studies,a generalized geometric QSLT was introduced.[14]For a comprehensive study of the different definition of quantum speed limits,one can refer to Refs.[15,16].Also,there are some theoretical investigations which generalize the concept of QSLT to mixed states[17]and beyond the rotating-wave approximation.[18]Due to the fact that there is a close relation between the QSLT and fidelity,it would be possible to improve the bounds of QSLT in an open quantum system by introducing an alternative fidelity for quantum states.[19]Additionally,to obtain a better bound for the QSLT,the notion of QSLT for specific physical systems has attracted a great deal of attention.[20–26]The simplest quantum system for state preparation and quantum computation is a two-qubit quantum gate.[27]Among the different two-qubit quantum gates realizations,systems composed of two coupled quantum dots(QDs)have attracted a great deal of attention.In these systems the excess electron spin in each QD would be realized as the qubit.[28–32]As a consequence of vast applications of coupled QDs systems investigation of QSLT in these systems can provide us valuable information about the systems’operation.This motivates one to study the QSLT and the physical parameters,which possess crucial impacts on the behavior of the QSLT in these kinds of systems.

The two-qubit system in the present contribution is composed of two electrons which are confined in two adjacent QDs.In this two-qubit spin chain,the spin-spin and spin–orbit interactions possess a remarkable role.This motivates us to investigate the influences of spin–orbit interaction on the QSLT.In order to improve the model and to take into account more realistic conditions,the anisotropy of spin coupling as well as inhomogeneity of an external magnetic field are taken into account.Moreover,the influences of an external magnetic field and temperature on the behavior of QSLT are studied,based on the introduced approach in Ref.[11].The maximal speed of evolution in the present quantum system would be followed through the obtained results.In addition to the above mentioned interactions,also the spin relaxation is taken into account.This process in QDs is a non-Markovian process naturally.Therefore,the QSLT is studied in the context of the non-Markovian open quantum systems.

An important feature of the composite quantum systems is quantum entanglement which is a special kind of quantum correlation with no classical counterpart.[33]Quantum entanglement and entangled systems play a remarkable role in quantum technologies such as quantum teleportation[34]and quantum cryptography.[35]In addition,the notion of quantum entanglement has found a rigorous application in quantum metrology,high-precision spectroscopy[36]and quantum simulation.[37]As a consequence of theoretical and applied applications of quantum entanglement,its generation,control and preservation in the related physical systems are of interest.Therefore,the introduction,investigation and manipulation of systems which provide long lasting and controllable quantum entanglement are important issues in quantum technologies.Accordingly,the evolution of entanglement between the qubits in the introduced system is investigated.

The rest of this article is organized as follows:In Section 2,the physical system is introduced and its time evolution is studied.A brief introduction about the QSLT and its derivation is given in Section 3.The numerical results and the influence of the effective parameters on the QSLT and entanglement behavior are studied in Section 4.Finally,Section 5 is devoted to summary and conclusion.

2.The physical system

The physical system studied is two adjacent QDs which are in interaction with each other.[28,29]In the model,the spin of the excess electron in a single-electron QD is realized as the qubit,Fig.1.In such a chain consisting of such QDs,by varying the tunneling barrier between neighboring singleelectron QDs an electron could be confined in each QD.The electron transfer between two adjacent QDs could be manipulated by barrier potential.In magnetic materials,spin–orbit coupling is an important and fundamental interaction which possesses a crucial role in the spin evolution.[38]In order to obtain more insights about the QSLT evolution in the system under study,we are going to study the spin–orbit interaction effects on the QSLT.We suppose that the coupled QDs are located in an inhomogeneous magnetic field.Therefore,the spin–orbit interaction of a Heisenberg XYZ two-qubit system(the electron spin of each QD)in the presence of an inhomogeneous magnetic field will be investigated.The coupled QDs(two qubits)constitute a two-qubit anisotropic Heisenberg XYZ model.The experimental realization of spin manipulation in coupled QDs can be found in Ref.[39].Also,contribution of hyperfine and spin–orbit interaction in weakly coupled InAs QDs can be followed in Refs.[40–42].The Hamiltonian of this system in the presence of the inhomogeneous magnetic field and spin–orbit interaction may read[43]

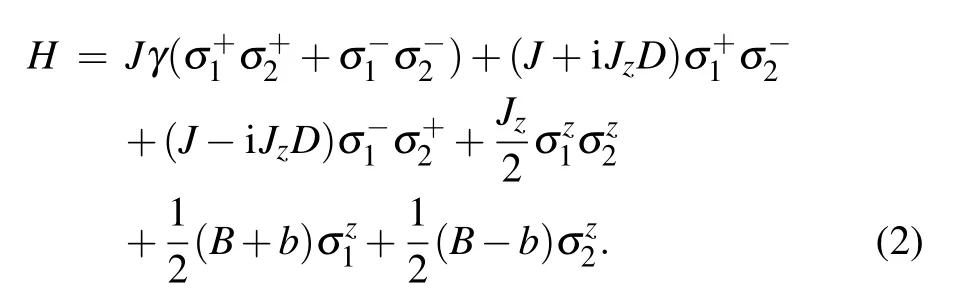
The QSLT determines the time which is necessary for the evolution of two distant initial and final quantum states to each other.[1,2]This means that the QSLT is related to a bound on the time which is needed for a state to reach a fidelity relative to the initial state.According to this description,the QSLT is obtained from the time evolution of the system.Since the system under study is an open quantum system,its time evolution would be followed through the quantum master equation.Moreover,the present system experiences a non-Markovian dynamics.Therefore,we suppose that the density matrix of the system is obtained from a time convolutionless master equation[48]

In this equation,ρBrepresents the environment state,and partial trace over the environment degrees of freedom is shown by TrB.Also,the interaction Hamiltonian between the system and environment,Hint,in the interaction picture with respect to the environment free Hamiltonian is shown by HI(t).It should be noted that the introduced approach,i.e.,the time convolutionless master equation,has been used to study the electronphonon interaction[50]and the spin-boson model under non-Markovian dynamics.[51]Inserting the HI(t)in Eq.(3),under the second order Born approximation,the following integrodifferential master equation determines the time evolution of the system:

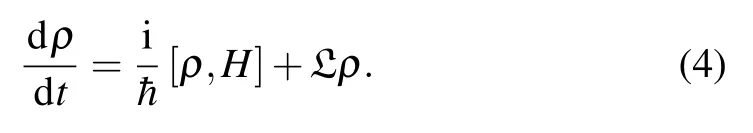
The first term governs the unitary evolution of the system.In this equation,H represents the Hamiltonian of system which is given in Eq.(2).The second term stems from the relaxation dynamics.The relaxation term originates from the second term on the right-hand side of Eq.(3).Using the interaction Hamiltonian between the system and environment in the interaction picture,the relaxation term in Eq.(4)is obtained as follows:

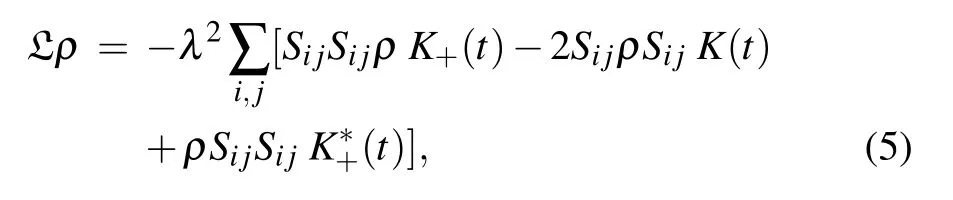
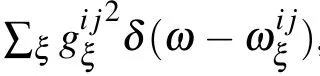
3.Quantum speed limit time of the coupled QDs

The main purpose of present contribution is to obtain the QSLT for an open two-qubit system(double QDs).The state evolution of system is governed by the master equation.As a consequence of the environment nature,the system under investigation experiences a non-Markovian evolution.The notion of QSLT in open quantum systems is investigated via different approaches.[9–11,54]Each of these approaches possesses specific bounds on the QSLT.The introduced approach in Ref.[11]leads to both Mandelstam–Tamm and Margolus–Levitin bounds.Therefore,we employ this approach to investigate the QSLT.The Bures angle between the initial and final states of the quantum system is defined as[55]

Without loss of generality,the initial state of the system is selected as a pure state,ρ0=|ψ0〉〈ψ0|.The dynamical velocity corresponding to the evolution of the density matrix determines the QSLT.The time derivative of the Bures angle gives the velocity of state evolution,

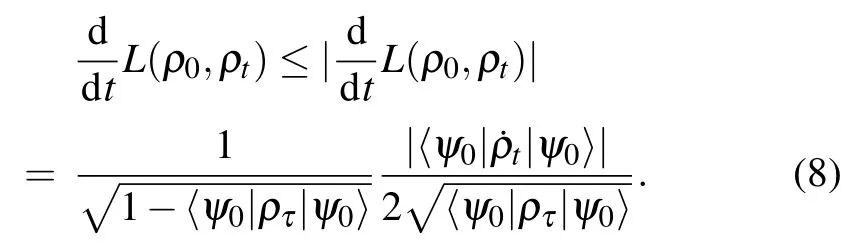
Invoking the definition(7),this relation can be cast to the following form:

The dynamics of the system is governed by a master equation,i.e.,in the present system,Eq.(4)can be written as

where L represents the positive generators of the dynamical semigroup,Λt=exp(Ltt).Following the introduced approach of Ref.[11]the QSLT is obtained as

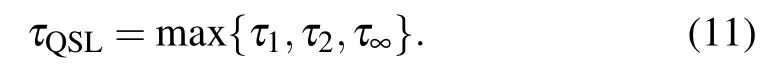
Here,the following notation is used:[19]

where

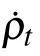
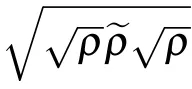
4.Numerical results and discussion

Our purpose is to investigate the dynamics and evolution of QSLT as well as entanglement in the present system.As is evident,the present system includes a number of physical parameters whose effects on the QSLT and entanglement would be followed.An important point and an interesting feature of the two-qubit systems is the possibility of entanglement formation when the qubits are not entangled initially.That is,if the qubits are in state|↓↓〉,wether it would be possible to entangle them during their evolution.To study this point,the evolution of the QSLT and concurrence is shown in Fig.2,when the initial state of the system is selected as|↓↓〉.In this figure,different plots of each panel correspond to the different magnetic field inhomogeneity.This figure illustrates that the magnetic field inhomogeneity does not affect the studied quantities.Also,Fig.2(a)shows that as time elapses,the QSLT is increased.This means that in this system one cannot transfer the initial state to a desired final state.This is due to the dissipation which is originated from the magnetic environment.On the other hand,Fig.2(b)shows the entanglement evolution in this system.This panel illustrates that the non-entangled qubits in their ground state become entangled during their evolution and consequently their entanglement will wash out.In the absence of spin–orbit interaction and spin-spin anisotropy,it is impossible to reach an entangled state from initially separated state.Thus,this entanglement formation could be attributed to the spin–orbit interaction and spin-spin anisotropy.Therefore,the entanglement of the qubits when they are in their ground state originates from the spin–orbit interaction.

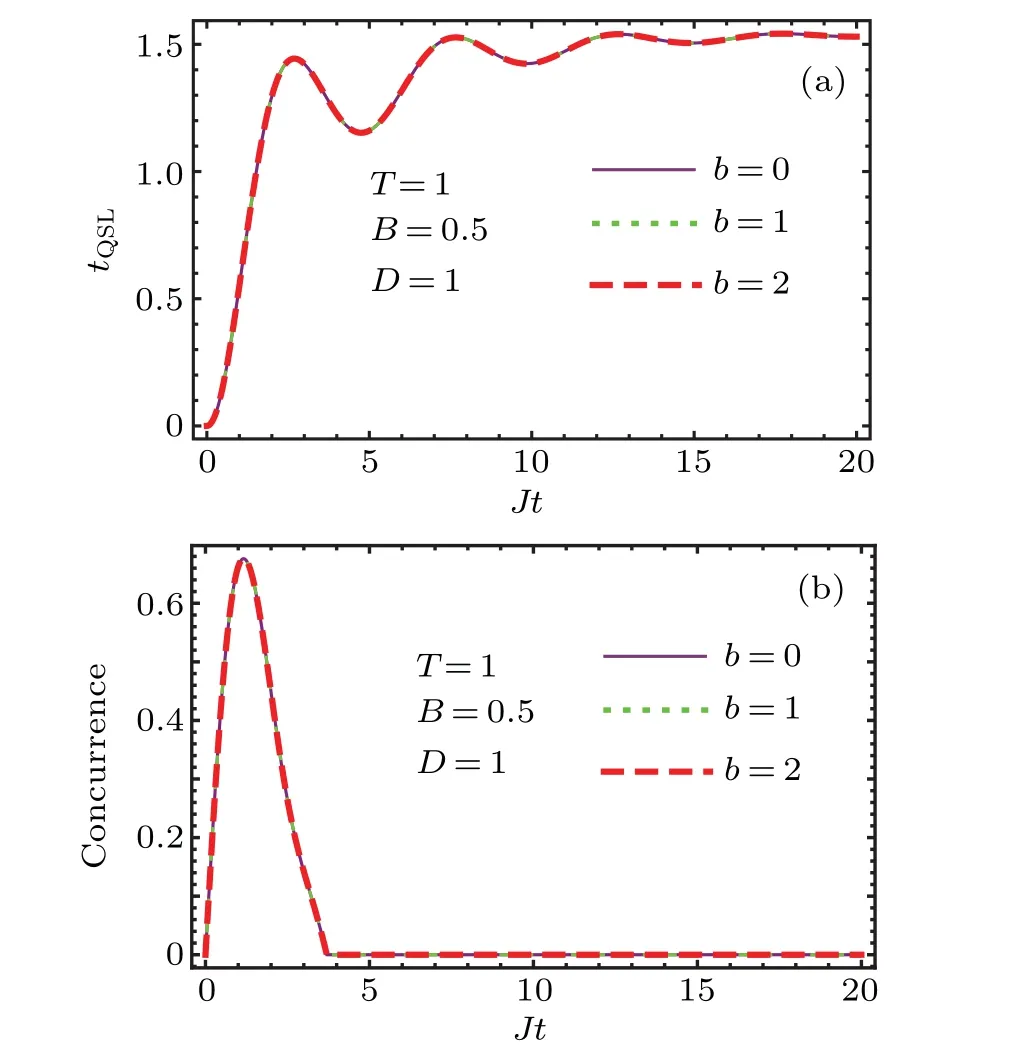
Fig.2.The time evolution of the QSLT and concurrence of the system by taking into account the spin–orbit interaction when the initial state of the system is selected as|↓↓〉.In each panel,different plots correspond to the different values of inhomogeneity of the magnetic field.In this figure,the other physical parameters are selected as T=1,B=0.5,D=1,γ=0.5,and Jz=0.5.

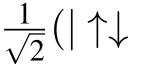
Fig.3.The time evolution of the QSLT and concurrence of the two qubitsinthe presence of thespin–orbitinteractionwhen the qubitsare initiallyentangled as|ψ0〉=.Ineach panel,different plots correspond to different magnetic field inhomogeneity.The parameters are selected as T=1,B=0.5,D=1,γ=0.5,and Jz=0.5.

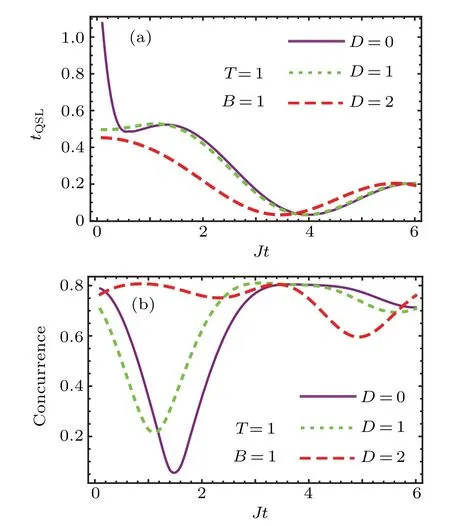
Fig.4.The dependence of the QSLT and concurrence on the magnetic field inhomogeneity.Here the initial state of the system is selected the same as that in Fig.3.Different plots in each panel correspond to different spin–orbit coupling constants(the norm of the Dzyaloshinski–Moria vector).In this figure,the magnetic field is selected as B=1,the temperature is chosen as T=1 and the time is selected as Jt=1.Moreover,we have selectedγ=0.5 and Jz=0.5.

An important quantity which possesses a crucial role in the system evolution is the magnetic field inhomogeneity.This parameter would be considered as an experimental control parameter.On the other hand,the dependence of the studied quantities on this parameter provides us knowledge about the role of magnetic field in the dynamics.The influences of this parameter are depicted in Fig.4.In this figure the dependence of the QSLT and concurrence on the magnetic field inhomogeneity is illustrated.Figure 4(a)shows that the increment of the magnetic field inhomogeneity leads to the QSLT decrement.That is,by increasing the inhomogeneous magnetic field we can decrease the minimum time required to transfer a quantum state into an other distant distinguishable state.On the other hand,the influences of the magnetic field inhomogeneity on the concurrence are illustrated in Fig.4(b).It shows that by increasing the magnetic field inhomogeneity the concurrence is decreased and finally this entanglement measure is increased.Moreover,by increasing the spin–orbit coupling strength the initial decrement of the entanglement is compensated for.It seems that the magnetic field inhomogeneity causes the two spins to experience the different interactions.Therefore,the qubits would be distinguished and consequently their entanglement will washed out.However,in the strong magnetic field inhomogeneity their entanglement is increased.Thus,the magnetic field inhomogeneity and spin–orbit coupling strength possess crucial influences on the behavior of the studied quantities.

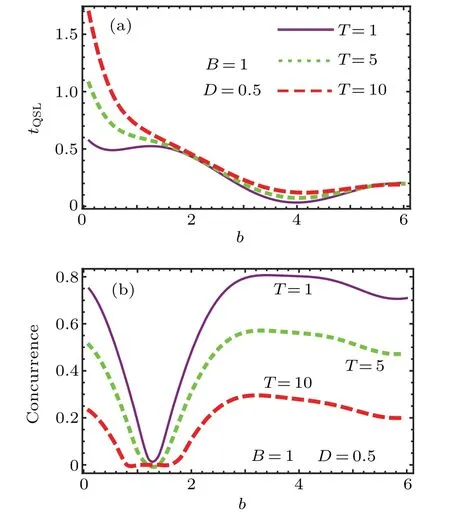
Fig.5.The influences of the magnetic field inhomogeneity on the QSLT and concurrence whereas the temperature is changed.Different plots in each panel correspond to the specific temperature.The spin–orbit coupling constant and magnetic field strength are chosen as D=0.5 and B=1.Also,time is selected as Jt=1.Other parameters are the same as before.The initial state of the system is the same as that in Fig.3.

Temperature is an important quantity which possesses the crucial influences on the system evolution.By studying the effects of temperature,we can follow the influences of the environment on the system evolution.The effect of temperature on the QSLT and concurrence is illustrated in Fig.5.In this figure the QSLT and concurrence are plotted versus the magnetic field inhomogeneity whereas the different plots in each panel correspond to the given temperature.Figure 5(a)illustrates that the magnetic field increment leads to the QSLT decrement.On the other hand,the temperature increasing is compensated by the magnetic field.We expect that the temperature increasing leads to the QSLT increment.However,Fig.5(a)shows that at elevated temperatures the magnetic field increment prevents the increasing QSLT.Figure 5(b)illustrates that the temperature increasing leads to the disentanglement.At elevated temperatures there is a distance in which concurrence is equal to zero.In Fig.5(b),after disentanglement for small magnetic inhomogeneity,the rebirth of entanglement occurs.The formation of entanglement is an important feature of this figure.Therefore,the temperature possesses a crucial role on the dependence of studied quantities on the magnetic field inhomogeneity.

5.Summary and conclusion

A basic system for quantum state transfer and computation is coupled QDs,which is studied in the present contribution.Two quantum features of this system,QSLT and entanglement,are investigated.The physical system is the electron spin in the separated coupled QDs which are imposed by an external magnetic field.The relaxation dynamics as a consequence of the hyperfine interaction between the electron spin and local nuclear spins is considered as a non-Markovian dynamics.Moreover,the role of spin–orbit interaction as well as the associated effects of the inhomogeneous external magnetic field and anisotropy of spin coupling are investigated.