基于双尺度约束模型的BN 结构自适应学习算法

戴晶帼 任佳 董超 杜文才

贝叶斯网络(Bayesian network,BN) 理论为不确定性知识的表示,节点间复杂关系的表达和信息融合推理提供了有效的模型框架[1-3].然而,与其他图形化模型学习方法类似,BN 也存在研究对象节点增加导致候选结构数量呈指数级增长的问题.因此,从大规模候选结构集合中快速,准确地获得一个与数据样本匹配程度最优的结构模型是BN 结构学习亟待解决的问题之一.

研究人员尝试利用条件独立性(Conditional independence,CI) 测试度量节点间的依赖关系,然后构造满足这些依赖关系的模型结构[4-6].但该类型学习方法运算次数一般为节点个数的指数次幂,当面对节点数量较多的复杂网络时,CI 测试效率较低.与此同时,研究人员将模型先验信息作为约束条件,并与结构评分函数和搜索算法组合,共同完成BN 结构学习[7-10].但该类型方法在模型先验信息不准确或发生错误的情况下,将导致结构学习结果精度低或陷入局部最优.为此,文献[11]通过构建不确定先验信息的评分函数并设计先验搜索算子,提高对错误先验信息的适应能力.但该方法并不能完全消除错误先验信息对BN 结构学习产生的负面影响.此外,研究人员将节点间依赖关系检验与结构优化学习方法相结合,进行无先验信息情况下的BN 结构学习[12-13].在该思路下,文献[14] 提出了一种混合式BN 结构学习方法,该方法通过计算互信息量(Mutual information,MI) 构造基于支撑树权重矩阵的节点序适应度函数,利用改进遗传算法(Genetic algorithm,GA) 获得节点排序,最后将节点排序作为K2 算法的输入进行结构学习;Wong 等和Ji 等分别将低阶CI 测试引入进化算法和蚁群优化算法,利用CI 测试辨识部分节点对的独立关系以缩小结构搜索空间,在此基础上利用评分函数和启发式搜索以获得BN 结构[15-16];Li 等则提出I-GREEDY-E 算法[17],该算法首先在空图上计算节点间的MI 以确定无向边,然后利用CI 测试确定边的指向,最后在等价类模型空间中利用贪婪搜索算法获得BN 结构.上述学习方法在无先验信息的情况下实现了对结构搜索空间的约束,并在约束空间内利用搜索方法获得了模型结构,一定程度上提高了多节点复杂网络结构的学习效率.然而,在无先验信息的情况下,以CI 测试或MI 检验为约束条件构造的结构搜索空间尺度固定,无法在结构学习过程中动态调整结构搜索空间的规模大小,易导致潜在最优解丢失.

针对上述问题,提出基于双尺度约束模型的BN 结构自适应学习算法(BN structure adaptive learning algorithm based on dual-scale constraint model,DSC-AL).该算法将最大互信息(Maximum mutual information,MMI) 和CI 测试结合建立结构搜索空间的大尺度约束模型,限制BN 结构搜索空间的规模,完成结构搜索空间的初始化.借鉴GA迭代寻优过程完成BN 结构学习.在迭代寻优过程中建立小尺度约束模型完成搜索空间动态调整,构建变异概率的自适应调节函数,提高GA 全局搜索能力.在实验仿真中,选择了不同节点规模的标准BN 模型和不同样本量对DSC-AL 算法的有效性进行测试,并通过与Lee 等提出的基于双重GA 编码的BN 结构学习算法[18]和Gheisari 等构建的基于粒子群优化的BN 结构学习方法[19],以及经典的K2算法[20]进行性能对比,验证DSC-AL 算法的性能.

1 问题描述

为达到大尺度约束模型完成结构搜索空间的初始化,小尺度约束模型实现结构搜索空间动态缩放的目的,在观测样本驱动下,DSC-AL 算法将MI 和CI 测试相结合辨识节点间的依赖或独立关系,形成限制结构搜索空间的大尺度约束模型.然而受MI和CI 测试方法辨识精度的影响,可能导致结构搜索空间约束不合理,将会出现以下两种情况,即约束尺度过大将最优结构排除在结构搜索空间之外,或约束尺度较小导致结构搜索空间规模依然较大.因此,还需要建立小尺度约束模型完成结构搜索空间动态缩放.DSC-AL 算法框架如图1 所示.

图1 DSC-AL 算法框架示意图Fig.1 The framework of DSC-AL algorithm

根据图1 给出的算法框架,大尺度约束模型作用于算法的初始阶段,通过剔除不满足约束条件的BN 模型限制结构搜索空间,而小尺度约束模型针对GA 种群中的每一个个体,在迭代寻优过程中,通过删除不满足约束条件的连接边调整每个个体表示的BN 结构.DSC-AL 算法为实现结构搜索空间小尺度动态缩放,降低GA 结构寻优过程发生早熟收敛的概率,需要解决以下三个关键问题:

1) 小尺度约束模型需要随GA 学习进程不断调整,达到动态缩放结构搜索空间的目的;

2) GA 学习进程中若产生新个体,需要反复检测无环性,并使用修复算子对无效结构进行无环修复,这将导致算法的时间成本增加,学习效率下降;

3) GA 学习进程需要保持种群多样性以及减少对优势基因的破坏,以降低学习方法陷入局部最优的可能性.

2 双尺度约束模型

2.1 大尺度约束模型

包含n个节点的BN 可生成的结构个数如式(1) 所示[21]:

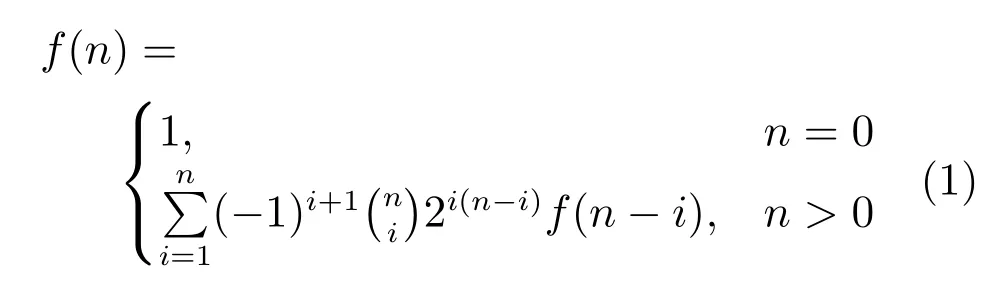
由上式可知,BN 结构搜索空间规模随着节点个数的增加呈指数级增长.为限制BN 结构搜索空间,利用节点连接边存在性约束与节点连接边缺失性约束[22]构建大尺度约束模型.

1) 节点连接边存在性约束

BN 中的节点x与节点y之间的MI 可以采用式(2) 进行计算:

式中:r和s分别表示节点x与节点y的状态个数,ai是x的第i个可能状态值,bj是y的第j个可能状态值.两个节点之间的MI 越大,两者之间的依赖性越强,即两个节点间可能存在一条连接边.

2) 节点连接边缺失性约束

CI 测试在给定观测样本和约束集Z的基础上,采用卡方检验判定原假设H0:I(x,y |Z)是否成立.式(3)中统计量χ2服从自由度为(r－1)×(s－1)×t的分布,其中t表示约束集Z的状态个数,即

根据节点连接边存在性约束与节点连接边缺失性约束,主要通过以下6 个步骤构建大尺度约束模型:

a) 利用MI 计算每个节点与其他节点之间的依赖程度大小;

b) 将MI 的计算结果排序,获取相应的MMI,找出与各节点依赖程度最高的相关节点.由于MI的对称性,即I(x;y)=I(y;x),每个节点的MMI所对应的连接边是无向的;

c) 随机给定连接边指向,确定BN 结构的节点顺序.根据该节点序列,剔除搜索空间中不满足该约束条件的候选结构,从而缩小结构搜索空间;

d) 根据c) 获得的节点序列建立相应的邻接矩阵,该矩阵的行序对应节点序列.由于节点序列中需要满足父节点排在子节点的前面,因此只需考虑上三角邻接矩阵.将矩阵的上三角部分中的所有元素设置为1.然后根据以下步骤中CI 测试的结果,修改满足条件独立的节点对所对应的矩阵元素;

e) 考虑到高阶CI 测试的不可靠性且较高的计算复杂度[23],采用一阶CI 测试,即|Z|=1,利用式(3) 计算邻接矩阵中所有节点的卡方统计量,储存每一个节点与其他节点之间的CI 测试结果中对应的最大p-值;

f) 将显著性水平α(初始值随机给定) 作为判断条件独立性的阈值.若最大p-值大于α,则两节点之间无连接边存在,因此将上三角邻接矩阵中的元素1 修改为0.在此基础上可对c) 中获得的结构搜索空间完成进一步缩放.

2.2 小尺度约束模型

根据构建大尺度约束模型的步骤f),发现利用CI 测试辨识节点独立性关系的精度与其显著性水平α取值相关.若α取值过小,易出现网络的部分连接边被永久删除,极有可能丢失潜在最优解;若α取值过大,结构搜索空间规模依然巨大,且候选结构中可能存在较多错误连接边,导致结构学习的效率和精度下降.因此,需要小尺度约束模型控制显著性水平α的更新,实现对结构搜索空间的动态缩放.

显著性水平α的更新主要依赖结构复杂度评估函数对GA 产生的每一代新的BN 结构的复杂度评估.根据评估结果产生更新后的αnew完成结构搜索空间的进一步缩放,更新后的结构搜索空间以及更新后的αnew将作用于GA 迭代搜索过程(相关内容将在第3 节进行介绍),小尺度约束模型工作原理如图2 所示.

图2 小尺度约束模型工作原理Fig.2 The working principle of small-scale constraint model

图2 中的结构复杂度评估函数是在BIC 评分函数的基础上获得的.考虑到BIC 评分函数是一种带惩罚函数的极大似然函数评分方法[23],评分函数中的第二项能够对BN 结构复杂度进行评估,因此可利用BIC 评分函数中的第二项对α进行动态更新.BIC 评分函数如式(4) 所示,即

式中:n表示结构中的节点个数,qi表示节点xi的父节点集合的状态数,ri表示节点xi的状态数,mijk是观测数据中满足节点xi的父节点集合为第j个状态且节点xi为第k个状态的样本个数,是观测数据样本总数.BIC评分的第二项是描述BN 结构复杂度的惩罚函数,结构复杂度越高,相应的惩罚函数值越大,如式(5)所示:

根据小尺度约束模型的工作原理,构建小尺度约束模型主要通过以下3 个步骤实现:

a) 利用式(5) 计算当代种群中每个个体的结构复杂度penaltyk;

b) 将上一步骤中计算得到的penaltyk与历史最优个体的结构复杂度penaltybest比较;若penaltyk＜penaltybest,则选择输入口1;若penaltyk ＞ penaltybest,则选择输入口3;若penaltyk=penaltybest,则选择输入口2.将更新后的αnew作为种群个体CI 测试的新的显著性水平;

c) 利用更新后的显著性水平αnew调整结构搜索空间.

需要说明的是,步骤b) 中根据复杂度评估结果更新α,即当种群个体的结构复杂度小于历史最优个体的结构复杂度时,需要增加该个体结构的连接边,减少CI 测试时满足条件独立性关系的节点对的数量,即提高显著性水平α,因此在α更新过程中选择输入口1,此时αnew=α+Δα;当种群个体的结构复杂度大于历史最优个体的结构复杂度时,应该减少结构的连接边数量,即降低显著性水平α,因此在α更新过程中选择输入口3,此时αnew=α－Δα;若种群个体和历史最优个体有相同的结构复杂度,此时,α的取值保持不变,因此在α更新过程中选择输入口2.

在GA 迭代寻优过程中存在新个体适应度不及前代个体的情况.DSC-AL 算法通过联赛选择算子和精英保留机制将前代最优个体直接选入下一代中进行迭代寻优,当代种群中的最优个体即为历史最优个体.将当代种群中每一个个体与该最优个体的结构复杂度进行比较,更新显著性水平.此外,BIC评分函数的罚项用于复杂度评估具有节点可分解性[8],以节点为单位将每个节点的结构复杂度用向量的方式保存.在迭代寻优过程中通常只有少数节点的结构产生变化,因此每次迭代只需更新个体表示的BN 结构中少数节点的结构复杂度.在动态调整显著性水平时直接利用结构复杂度向量中对应元素进行计算,可以降低计算复杂性.

3 基于双尺度约束模型的BN 结构自适应学习算法

3.1 BN 结构自适应学习过程

基于双尺度约束模型的BN 结构自适应学习算法设计思路如下:

1) 设计种群个体的编码方案.将节点顺序和CI测试的显著性水平α引入种群编码.其目的主要包含两个方面:避免迭代寻优过程中对新个体无环性的反复检验或修复无效结构;利用双尺度约束模型限制结构搜索空间,提高多节点复杂结构的学习精度和迭代寻优的收敛速度.

2) 动态调节变异概率.在改进GA 的进化过程中,为保持种群多样性与结构继承性之间的平衡,通过动态调节变异概率以提高结构学习的收敛速度和全局寻优能力.

基于双尺度约束模型的BN 结构自适应学习算法流程如图3 所示.

图3 DSC-AL 算法流程图Fig.3 The flowchart of DSC-AL algorithm

3.2 编码生成

BN 结构G=(X,E) 是一个有向无环图(Directed acyclic graph,DAG).令节点集合X={xi}i=1,2,···,n代表领域变量,节点间的有向边E={eij} 代表节点间的直接依赖关系,pa(xi) 表示节点xi的父节点集合.使用GA 完成BN 结构学习,可使用邻接矩阵A=(eij) 对BN 结构进行编码表达[24].然而随机生成的邻接矩阵,其对应的结构无法保证BN 无环要求.为此设计一种新的编码方案以解决该问题.

新的个体编码方案的表达式如式(6) 所示:

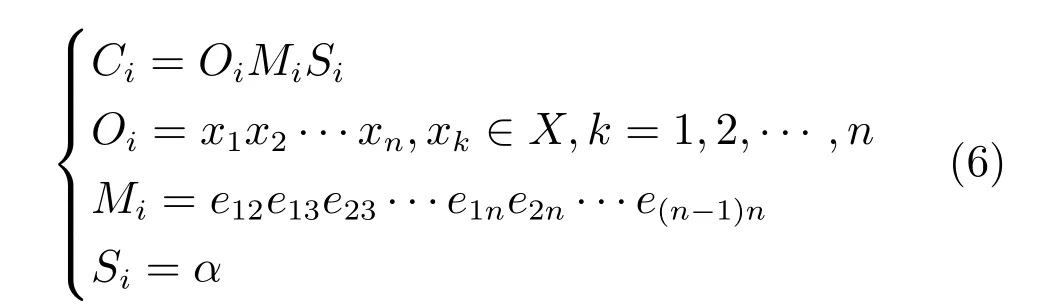
式(6) 中:Ci表示第i个种群个体,Oi代表BN 结构的节点顺序,Si代表CI 测试的显著性水平,Mi表示根据第i个种群个体的节点序列构建的上三角邻接矩阵,其中元素取值如式(7) 所示.在节点顺序中,每一个节点的父节点都必须排在该节点的前面.这一原则使得遗传算子是封闭的[25],即在进化过程中无需检测或修复种群个体,能够保证产生的新个体是无环的.此外,将CI 测试的显著性水平α加入个体编码中,使得显著性水平α随迭代过程自适应更新.

为了说明搜索空间中所有的BN 结构均能采用上述个体编码方案进行表达,给出相关定理,并进行证明.

引理1[18].任何一个具有n+1 个节点的DAG都能够被分解为一个根节点(或叶节点) 和一个具有n个节点的DAG 的连接.

定理1.任何一个具有n个节点的DAG 都能够使用一个确定的节点排序和与该序列对应的上三角邻接矩阵以及CI 测试的显著性水平进行表示.

证明.由CI 测试的定义可知,显著性水平大小决定两节点之间是否存在连接边,并且该连接边是无向边,因此并不影响节点排序.当节点排序确定后,CI 测试的显著性水平只决定该序列对应的上三角邻接矩阵中的元素,即条件独立的两节点对应的矩阵元素必为0.因此,只需选择适当的显著性水平保证条件独立的节点对集合为DAG 中元素为0 对应的节点对集合的子集.

下面用数学归纳法证明.

当n=2 时,命题显然成立.假设x1是根节点,x2是叶节点,则存在节点排序为O=12,对应的上三角邻接矩阵M=,此时显著性水平α的取值保证节点x1与x2不是条件独立;

假设命题对具有n个节点的DAG 成立.考虑G为任一具有n+1 个节点的DAG.根据引理1,G可分解为一个根节点(或叶节点) 和一个具有n个节点的DAG 的连接.若G分解为一个根节点和一个具有n个节点的DAGG′的连接,由假设可知,G′可由一个节点排序O及其对应的上三角邻接矩阵M和显著性水平α表示,其中

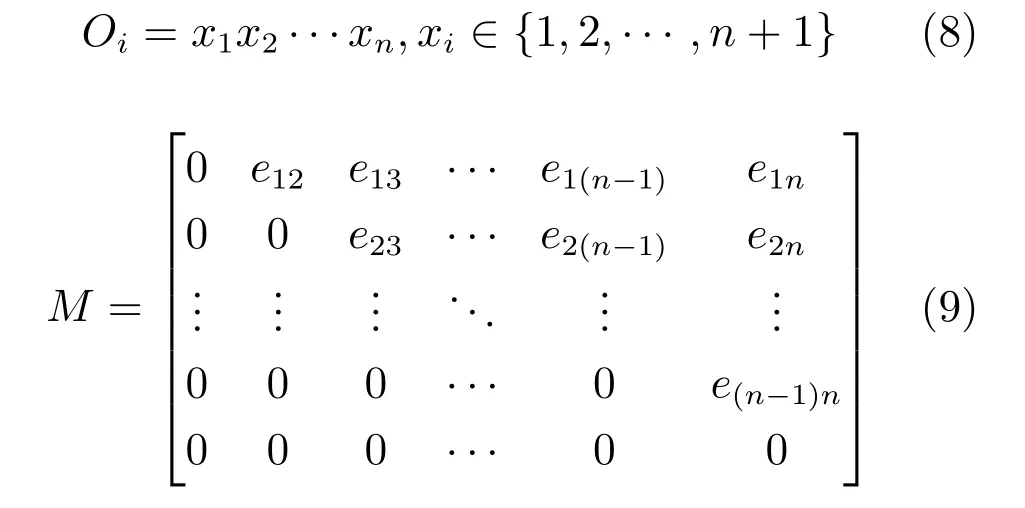
根据显著性水平α的取值,条件独立的节点对所对应的eij=0,即在G′中该节点对之间必无连接边.若G的根节点为xn+1,则G的节点排序可表示为O′=xn+1x1x2···xn,故其对应的上三角邻接矩阵为

其中为1×n的矩阵,在加入根节点后,调整显著性水平α的取值,使得满足CI 测试的条件独立关系的节点对集合为G中无连接边的节点对集合的子集.

同理,若G分解为一个叶节点和一个具有n个节点的DAGG′′的连接,则G′′可由一个节点排序O及其对应的上三角邻接矩阵M和显著性水平α表示,如式(8) 和式(9) 所示.若G的叶节点为xn+1,则G的节点排序可表示为O′=x1x2···xnxn+1,故其对应的上三角邻接矩阵为

其中为n×1 的矩阵,在加入叶节点后,调整显著性水平α的取值,使得满足CI 测试的条件独立关系的节点对集合为G中无连接边的节点对集合的子集.故命题对任一具有n+1 个节点的DAG 成立.

3.3 自适应变异算子

GA 中变异操作的作用是保持种群的多样性.传统的GA 变异算子所使用的变异概率是一个固定值,即GA 每一代种群中的所有个体都使用相同的变异概率,无法随GA 迭代过程发生改变.变异概率取值固定时,若变异概率取值太小,在GA 迭代的中后期,种群多样性将会急剧下降,GA 不易跳出局部极值点;若变异概率取值过大,极易破坏种群个体的优势基因,从而导致GA 的收敛速度缓慢.为此,设计一种基于种群个体适应度的自适应变异算子,在GA 迭代过程中为不同阶段的种群个体以及同一种群中的不同个体提供变异概率,确保种群的多样性,克服GA 的早熟收敛.

种群个体的适应度能够反应变异概率变化情况.当种群个体适应度逐渐趋于一致时,变异概率应该适度增大,以防止GA 迭代陷入局部最优;当种群个体的适应度较分散时,变异概率应该适度减小,使GA 迭代尽快收敛到全局最优解[26].因此,可通过种群的最大适应度fitmax和平均适应度fitavg来描述种群适应度的一致性,构建的变异概率pm的自适应调节函数如式(12) 所示.

式中:(g) 表示第g代种群中第k个个体的变异概率,为一常数,01,fitk表示第k个个体的适应度值,fitmax－fitavg的差值反映了种群适应度的集中情况,fitk与fitavg的比较则描述了第k个个体的优异程度.fitk的计算公式如式(13)所示:

式中:scorek是第k个个体所表示的BN 结构的BIC 评分,scoremin是当前种群中的最低BIC 评分,scoremax是当前种群中的最高BIC 评分.

在获得变异概率pm的基础上,若变异位置出现在表示上三角邻接矩阵的编码部分,则该位置上的基因由0 变为1 或者由1 变为0;若变异位置出现在节点顺序的编码部分,则随机选择另一个节点与该位置上的节点互换.需要注意,随机选定的个体变异位置将不包含显著性水平α的部分,即个体中的显著性水平α不参与变异.

3.4 其他算子

DSC-AL 算法的选择算子采用联赛选择方法从当前种群中挑选出优良个体作为父代执行交叉,变异操作.此外,算法使用单点交叉算子,具体实现过程如算法1 所示,其中关于交叉点位于种群个体编码的第一部分,即节点顺序的情况,图4 给出了一个实例.

算法1.交叉算子

输入.种群个体ind,交叉概率pc

输出.交叉后的新个体new-ind

1) 交叉概率pc→交叉位置pos;

2)pos出现在ind编码的第三部分,即显著性水平→不交叉;

3)pos出现在ind编码的第二部分,即连接边→从pos开始的后半段交叉;

4)pos出现在ind编码的第一部分,即节点顺序→二,三部分直接互换,第一部分按照图4 交叉.

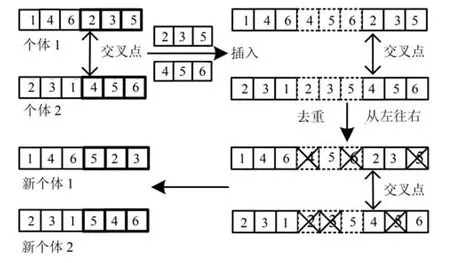
图4 节点顺序交叉方法Fig.4 The crossover of node order

4 仿真实验

4.1 实验方案设计

4.1.1 对比实验

1) 为验证DSC-AL 算法中各功能模块的有效性,选择的对比算法如下:利用随机初始种群替代大尺度约束模型的算法(DSC-AL+RdInit),采用固定显著性水平替代小尺度约束模型的算法(DSCAL+FixAlp),使用固定变异概率的算法(DSC-AL+FixP) 以及在进化过程中随机改变显著性水平的算法(DSC-AL+RdAlp);

2) 为验证DSC-AL 算法学习BN 结构的性能,采用下列算法进行对比实验:Lee 利用节点顺序和上三角邻接矩阵提出的基于双重GA 编码的BN结构学习算法(Dual genetic algorithm,DGA) 和Gheisari 等构建的基于粒子群优化的BN 结构学习方法(BN construction algorithm using particle swarm optimization,BNC-PSO) 以及K2 算法.

4.1.2 仿真模型及实验平台

1) 选用三种不同规模的标准BN 模型ASIA,CAR-DIAGNOSIS2 和ALARM 对结构学习方法进行测试,验证DSC-AL 算法对不同规模的BN 结构进行学习的性能,其中ASIA 模型为8 个节点的小规模网络,CAR-DIAGNOSIS2 模型包含18 个节点,ALARM 模型包含37 个节点.三种模型的拓扑结构如图5 所示;

图5 三种标准BN 结构示意Fig.5 Three benchmark BNs

2) 实验平台为Intel Core i5-5300U,2.30 GHz CPU,32 位的微机,操作系统为Windows 7,算法程序均在MATLAB R2014a 上编译.

4.1.3 仿真实验参数设置

1) 由于BN 中父节点集合的状态个数随父节点数量的增加呈指数级增长,为简化算法实现过程,在仿真实验中令每个节点的父节点个数不超过5 个;

2) 由于GA 和粒子群优化方法的迭代寻优过程具有很强的随机性,为保证对比实验能够充分反映每种算法的性能,除K2 算法外,其他迭代优化算法均独立仿真运行30 次完成测试.K2 算法是一种确定性算法,其学习结果与输入的节点顺序有关.为保证公平性,在不引入先验知识的情况下,随机给出不同的节点序列作为K2 算法的输入,同样执行30 次仿真实验;

3) DSC-AL 算法的参数设置如下:种群规模为200,联赛选择算子中联赛规模取4,交叉概率为0.9,变异算子中常数=0.1,小尺度约束模型中Δα=0.02;

4) DGA 的参数设置如下:种群规模为500,交叉概率为0.65,变异概率为0.05;

5) BNC-PSO 的参数设置如下:种群规模为200,其他参数与文献[19] 取值相同;

6) DSC-AL+FixAlp 算法的参数设置如下:显著性水平更新算子中α=0.05;

7) 在DSC-AL+FixP 算法中,变异概率为0.1;

8) 对比实验中,每种算法学习中小型网络:ASIA 和CAR-DIAGNOSIS2 模型的最高迭代次数均为300,学习大规模网络:ALARM 模型的最高迭代次数均为500;均采用BIC 评分准则对种群个体的适应度评估.

4.1.4 算法性能评价指标

1) 初始种群中最优结构的BIC 评分(IBIC);

2) 算法获得的最终结构BIC 评分(BIC);

3) 算法获得的最终结构与标准模型结构之间的汉明距离(SHD);

4) 算法运行时间(RT);

5) 获得最优解的迭代次数(BG).

4.2 仿真实验与结果分析

实验 4.2.1 和 4.2.2 分别在1 000 组ASIA 网络样本数据集 (ASIA-1000) 和2 000 组CAR-DIAGNOSIS2 网络样本数据集(CAR-DIAGNOSIS2-2000) 下对DSC-AL 算法各功能模块的有效性进行仿真;实验4.2.3 分别在2 000 组和5 000 组ALARM 模型样本数据集(ALARM-2000 和ALARM-5000) 下对DSC-AL算法的结构学习性能进行测试.

4.2.1 ASIA 模型仿真实验

以ASIA 模型为标准结构的仿真实验结果如表1 所示.表1 给出了ASIA-1000 样本数据集下,7种BN 结构学习算法的5 个性能指标平均结果,即表中每种算法的性能指标值为30 次重复实验的平均值,括号中的数据为标准差.在“数据集” 列中,括号中的数值为ASIA 模型对应的BIC 评分.由于K2 算法未使用GA,因此表1 中K2 对应的IBIC,RT 和BG 中无数据.

对表1 仿真结果的分析如下:

表1 ASIA 模型下不同算法结果对比Table 1 Comparisons of different methods on ASIA network

1) 在30 次的独立仿真实验中,DSC-AL 算法的平均结构汉明距离(SHD) 为1.3667,在7 种算法中最小.结构汉明距离越小表示算法学习到的结构越接近标准网络结构,即证明DSC-AL 算法学习获得结构与标准ASIA 模型结构相似度最高;

2) DSC-AL 算法的初始种群的平均BIC 评分(IBIC) 为－2375.1,比DGA 算法(－2406.9) 和DSC-AL+RdInit 算法(－2421.9) 的分值高,与其他对比方法的IBIC 分值接近.证明利用MMI 和CI 测试构造的大尺度约束模型对GA 种群进行初始化,能够有效提高初始化种群的适应度;

3) 在相同的终止条件下,DSC-AL 算法的平均运行时间(RT) 为103.4270 秒,比DGA 算法(173.9571 秒) 的用时短.表明DSC-AL 算法的学习效率优于DGA 算法.相较于基于DSC-AL 算法的修改方法,DSC-AL 算法需要利用大尺度约束模型完成种群初始化操作,且在迭代寻优过程中需要不断自适应调整CI 测试的显著性水平和变异概率,因此DSC-AL 算法耗时较长;

4) DSC-AL 算法的平均结构汉明距离(1.3667)远远小于K2 算法的平均结构汉明距离(7.5667).表明在无先验知识的情况下,DSC-AL 算法的学习精度远高于K2 算法,并且不需要依赖于专家经验.为了清晰地对比6 种结构学习算法(除去K2 算法) 的性能,图6(a)～6(c) 分别描述了在ASIA-1000 样本数据下的平均汉明距离,获得最优解的平均迭代次数和算法运行的平均消耗时间.由图6 可知,与DGA 算法相比,DSC-AL 算法能够使用较少的迭代次数获得最优的BN 结构;并且相较于DSC-AL+FixP,DSC-AL+RdAlp 和DSC-AL+RdInit算法,虽然DSC-AL 算法在相同终止条件下所耗费的时间较多,但是该算法学习到的最终结构明显优于其他算法,获得最优解的平均迭代次数也少于其他算法.但是在小规模ASIA 模型的仿真结果中,与DSC-AL+FixAlp 算法比较,DSC-AL 算法的优势并不明显.

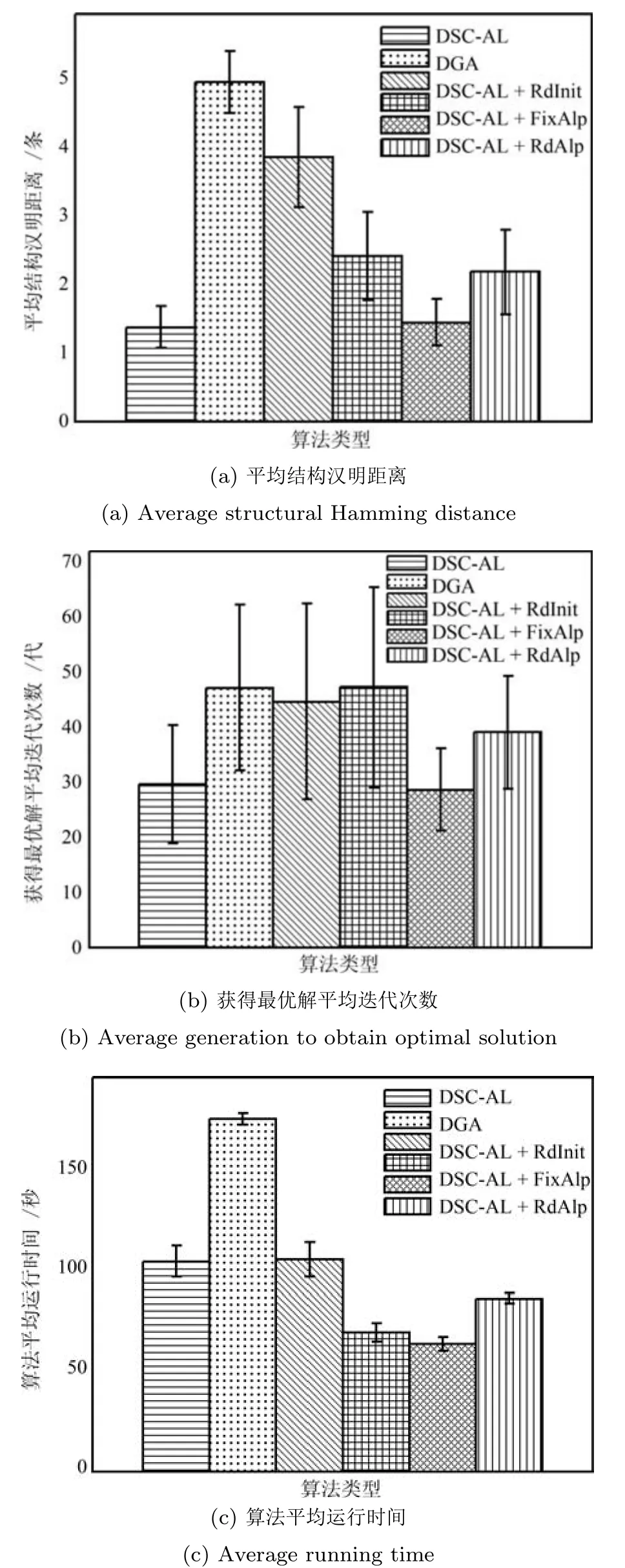
图6 6 种算法在ASIA-1000 数据集下的3 种性能指标的误差条形图Fig.6 Error bar graph of 3 measures for 6 algorithms on ASIA-1000 data set

图7 是在ASIA-1000 样本数据下分别运行30次,6 种算法(除去K2 算法) 获得最优结构的BIC评分平均值随迭代次数变化的曲线.由图7 可知,DSC-AL 算法初始种群中的最优结构评分相较于DGA 算法高,直至迭代终止,DSC-AL 算法最终结构的BIC 评分值始终高于DGA 算法,并且DSCAL 算法收敛速度比DGA 算法快.与其他修改算法对比,DSC-AL 算法的BIC 评分的平均值在迭代过程中始终高于DSC-AL+RdInit 算法,且DSC-AL 算法的收敛速度高于DSC-AL+FixP 算法和DSC-AL+RdAlp 算法,但是与DSC-AL +FixAlp 算法的趋势及大小无明显差异.

图7 ASIA-1000 下最优结构BIC 评分平均值变化曲线Fig.7 The curves of BIC scores for optimal structures on ASIA-1000 data set

图8 是在ASIA-1000 样本数据下分别运行30次,6 种算法(除去K2 算法) 获得的优于上一代种群的个体数平均值.由图8 可知,每种算法在迭代寻优过程的后期所获得的比上一代更优的结构个数都趋于零.然而即使将DGA 算法的种群规模放宽至500 (远远大于DSC-AL 算法的种群规模),该算法出现优于上一代种群的个体数平均值为零的情况的时间更早,即更容易陷入局部最优,发生早熟收敛.

图8 ASIA-1000 下优于上一代种群的个体数平均值变化曲线Fig.8 The curves of number of better individuals on ASIA-1000 data set

4.2.2 CAR-DIAGNOSIS2 模型仿真实验

以CAR-DIAGNOSIS2 模型为标准结构的仿真实验结果如表2 所示.表2 给出了CAR-DIAGNOSIS2-2000 样本数据集下,7 种BN结构学习算法的5 个性能指标平均结果,即表中每种算法的性能指标值为30 次重复实验的平均值,括号中的数据为标准差.在“数据集” 列中,括号中的数值为CAR-DIAGNOSIS2 模型对应的BIC 评分.由于K2 算法未使用GA,因此表2 中K2 对应的IBIC,RT 和BG 中无数据.

对表2 仿真结果的分析如下:

表2 CAR-DIAGNOSIS2 模型下不同算法结果对比Table 2 Comparisons of different methods on CAR-DIAGNOSIS2 network

1) 在30 次的独立仿真实验中,DSC-AL 算法的平均结构汉明距离(SHD) 为6.8000,该指标在7种算法中最小,表明该算法学习获得的结构与标准CAR-DIAGNOSIS2 模型相似度最高;

2) 在相同的终止条件下,DSC-AL 算法的平均运行时间(RT) 为520.6599 秒,比DGA 算法(856.7351 秒) 的用时短,表明DSC-AL 算法的学习效率比DGA 算法高.

图9(a)～9(c) 分别描述了上述6 种算法(除去K2 算法) 在CAR-DIAGNOSIS2-2000 样本数据下的平均汉明距离,获得最优解的平均迭代次数和算法运行的平均消耗时间.如图9 所示,可以获得与ASIA 模型仿真结果所显示的相同结论.此外,通过比较CAR-DIAGNOSIS2 模型和ASIA 模型的仿真实验结果,发现随着网络规模的增大,DSC-AL 算法的优势表现得更加明显.

图9 6 种算法在CAR-DIAGNOSIS2-2000 数据集下的3种性能指标的误差条形图Fig.9 Error bar graph of 3 measures for 6 algorithms on CAR-DIAGNOSIS2-2000 data set

图10 是在CAR-DIAGNOSIS2-2000 样本数据下分别运行30 次,6 种算法(除去K2 算法) 获得最优结构的BIC 评分平均值随迭代次数变化的曲线.由图10 可知,与ASIA-1000 样本数据下的仿真结果相似,与DGA 算法相比,从初始种群开始直至算法结束,DSC-AL 算法获得的每一代的最优结构性能更好,并且DSC-AL 算法收敛速度更快.此外,DSC-AL+RdInit 算法和DGA 算法的初始种群中最优结构评分低于其他算法,即上述两种算法的初始种群所表示的结构最差.

图10 CAR DIAGNOSIS2-2000 下最优结构BIC 评分平均值变化曲线Fig.10 The curves of BIC scores for optimal structures on CAR-DIAGNOSIS2-2000 data set

图11 是在CAR-DIAGNOSIS2-2000 样本数据下分别运行30 次,6 种算法(除去K2 算法) 获得的优于上一代种群的个体数平均值.如图11 所示,由于DGA 算法种群个体数为500,在迭代寻优过程的前期和中期,该算法获得的优于上一代种群的个体数的平均值最高,但是到迭代的后期,与ASIA 模型仿真结果相似,DGA 算法仍然最先出现比上一代更优结构个数为零的情况.

图11 CAR-DIAGNOSIS2-2000 下优于上一代种群的个体数平均值变化曲线Fig.11 The curves of number of better individuals on CAR-DIAGNOSIS2-2000 data set

4.2.3 ALARM 模型仿真实验

前面两小节的实验结果已经验证DSC-AL 算法各功能模块的有效性,为了进一步探究DSC-AL 算法的结构学习性能,以ALARM 模型为标准结构进行仿真实验,对比三种群智能优化算法,包括DSCAL,BNC-PSO 和DGA,结果如表3 所示.表3 分别给出了ALARM-2000 和ALARM-5000 样本数据集下,3 种结构学习算法的3 个性能指标平均结果,即表中每种算法的性能指标值为30 次重复实验的平均值,括号中的数据为标准差.在“数据集” 列中,括号中的数值为ALARM 模型不同数据集对应的BIC 评分.

对表3 仿真结果的分析如下:

表3 ALARM 模型下不同算法结果对比Table 3 Comparisons of different methods on ALARM network

1) 在ALARM-2000 和ALARM-5000 两个不同规模的数据集下,DSC-AL 算法的平均结构汉明距离(SHD) 在3 种基于群智能优化的BN 结构学习算法中均最小,表明DSC-AL 算法学习获得结构与标准AL-ARM 模型结构相似度最高,并且受到数据规模的影响较小;

2) 在相同的终止条件下,针对ALARM-2000和ALARM-5000 两个不同数据集规模,结合3种学习方法获得最优解的平均迭代次数(GB:225.8000＜267.7778＜498.1667,203.4000＜度和迭代寻优的收敛速度提高.与DGA 和BN315.9000＜498.3333) 和平均结构汉明距离(SHD) 的仿真结果可知,DSC-AL 算法能够使用最少的迭代次数获得与标准模型最相似的结构,表明在不同规模数据集下,DSC-AL 算法的收敛速度和BN 结构复原能力均优于DGA 和BNC-PSO 算法.

图12 和图13 是3 种基于群智能方法的BN 结构学习算法分别在ALARM-2000 和ALARM-5000样本数据下运行30 次获得最优结构的BIC 评分平均值随迭代次数变化的曲线.由图12 和图13 可知,在不同数据样本规模下,3 种算法评分平均值随迭代次数的变化趋势是相似的.DSC-AL 算法初始种群中的最优结构评分相较于DGA 和BNC-PSO 算法高,直至迭代终止,DSC-AL 算法学习到的结构评分值始终明显高于DGA 算法,但与BNC-PSO 算法获得的BN 结构的评分值差异小;此外,DSC-AL算法收敛速度比BNC-PSO 算法快,DGA 算法在迭代终止时并没有达到收敛状态.

图12 ALARM-2000 下最优结构BIC 评分平均值变化曲线Fig.12 The curves of BIC scores for optimal structures on ALARM-2000 data set

图13 ALARM-5000 下最优结构BIC 评分平均值变化曲线Fig.13 The curves of BIC scores for optimal structures on ALARM-5000 data set

仿真实验结果说明,在无先验知识的情况下,本文提出的DSC-AL 算法通过采用大小尺度约束模型和变异概率自适应调节函数,使得结构学习的精C-PSO 两种基于评分搜索的算法不同,DSC-AL 算法是一种混合学习方法,融合条件独立关系检验和智能优化方法.为缩小结构搜索空间,DSC-AL 算法采用一阶CI 测试和MMI 计算结果结合,假设n为变量数,在最坏的情况下算法需要进行O(n3)次CI测试和O(n2)次MI 计算.虽然与DGA和BNC-PSO 算法比较,DSC-AL 算法在进行迭代寻优之前增加了大尺度约束模型过滤无效结构的步骤,但是在后续的评分搜索阶段,DSC-AL 算法利用节点顺序设计编码方案,使得该算法无需进行无环检验,并且通过小尺度约束模型动态更新结构搜索空间,进一步剔除无效结构,提高迭代寻优的搜索效率.相较于DGA 和BNC-PSO 算法,DSC-AL 算法完成BN 结构学习任务的性能更优,并且受到数据样本规模的影响小.

5 结论

从大规模候选结构集合中快速,准确地获得一个与数据样本匹配程度最优的结构模型是BN 结构学习亟待解决的问题之一.为此,提出了一种基于双尺度约束模型的BN 结构自适应学习(DSC-AL) 算法,解决了在无先验知识的情况下,通过数据样本信息动态限制搜索空间,高效挖掘节点间相关性的BN结构学习问题.该算法在MMI 和CI 测试的双重约束条件下产生GA 的初始种群,获得BIC 评分高的种群个体,加快收敛速度;通过在个体编码中引入CI 测试的显著性水平,DSC-AL 算法在进化过程中利用更新模型不断调整显著性水平的大小,使得对应的搜索空间动态,合理地变化,提高算法的全局搜索能力;同时充分利用种群个体的适应度分布自适应地调节变异概率,克服算法的早熟收敛.仿真结果验证了本文算法对解决BN 结构学习问题的有效性,该算法能够确保种群个体的多样性,提高结构学习的精度和迭代寻优的收敛速度.