生成式不完整多视图数据聚类

赵博宇 张长青 , 陈 蕾 ,3 刘新旺 李泽超 胡清华

在实际应用中,数据通常从不同的角度采集,称为多视图数据[1-2].多视图学习研究[2-7]表明,有效利用不同视图之间的一致性和互补性可以显著提高任务(如多视图聚类/分类)性能.在聚类方面,已有大量的研究将单视图聚类扩展到多视图聚类.在这些方法中,基于自表示的多视图子空间聚类[8-12]方法通过可学习的关系矩阵处理复杂的高维数据,取得了显著效果.最近,一些相关研究[13-15]将谱聚类和自表示关系图联合优化,进一步提高多视图融合效果.

尽管基于自表示的多视图子空间聚类技术已经引起了人们的广泛关注,并取得了很好的性能,但是这些方法只适用于具有完整视图的数据,不能处理具有缺失视图的数据.对于视图缺失的情况,现有的方法大多是先对缺失值进行补全,然后对后续任务应用传统的多视图学习算法.广泛使用的数据补全方法之一是矩阵补全[16-17],它基于低秩假设,对于随机缺失情况具有较好的效果.基于深度学习的补全方法[18-22]通常通过将问题建模为视图转换,从可用视图生成缺失视图.这些方法侧重于缺失视图的填充,而不是具体的分析任务(如聚类),因此不能保证后续任务的性能.现有的不完整多视图聚类方法[23-25]没有考虑与缺失视图对应的(互补)信息的一致性,因此在挖掘不同视图之间的相关性时缺乏合理性和鲁棒性.

上述解决视图缺失问题的方法主要有以下局限性:1)对于具有任意视图缺失模式的数据样本,当前的补全方法通常不够灵活.此外,对于具有较多视图的数据,视图缺失模式(即可用视图的组合)将变得更加复杂,这将导致大多数现有视图补全方法无法使用;2)现有缺失视图聚类方法没有有效地利用多个视图之间的高阶相关性[8-9,11].为了解决上述问题,本文提出了一种新颖的多视图聚类方法,它可以同时补全缺失的数据和探索多个视图之间的高阶相关性.所提模型的框架如图1 所示.

图1 同时用 P (X|H) 对隐空间 H 进行建模,并基于隐表示生成完整特征.根据完整的数据,GM-PMVC 将子空间表示集成到一个张量中,可以挖掘多视图数据高阶相关性Fig.1 Illustration of generative model for partial multi-view clustering (GM-PMVC).Given incomplete multi-view data,we simultaneously model latent space H by P (X|H) and generate complete feature based on latent representation.According to the completed data,GM-PMVC integrates subspace representation into a tensor which can effectively explores higher-order correlations equipped with low-rank constraint

本文的贡献总结如下:1) 针对不完整视图数据,提出了一种新的多视图子空间聚类算法,该算法能够在统一的框架下补全缺失数据并进行多视图聚类.因此,数据补全和聚类可以迭代地相互促进;2) 与现有的不完整多视图聚类算法相比,该算法能够灵活地处理具有任意视图缺失模式的数据,并利用生成模型和高阶张量充分挖掘不同视图之间的相关性;3) 利用增广拉格朗日交替方向最小化(ALADM)方法对算法进行了有效的优化,并在不同的数据集上进行了充分实验.结果表明,在不同的缺失率下,该算法比现有算法具有更好的性能.

1 张量奇异值分解(t-SVD)及其核范数(t-TNN)

本文所使用的主要符号和定义.如表1 所示:

表1 符号与定义Table 1 Notations and definitions

为了引入t-SVD 和其产生的张量核范数,本文首先介绍相关的张量操作.具体地,假设对于任意三阶张量表示为B∈Rn1×n2×n3,则其块循环矩阵可以表示为:

块对角化矩阵及其逆过程可以定义为:

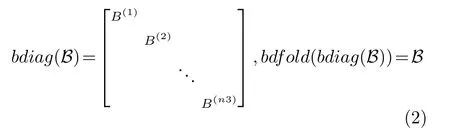
张量展开unfold(·) 及其逆过程fold(·) 定义为:为了简明表示,相关定义如下:

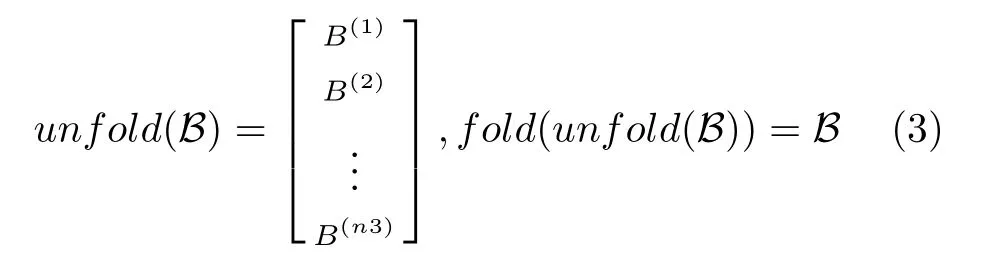
定义 1.张量积 (t-product):张量B∈Rn1×n2×n3和C∈Rn2×n4×n3之间的张量积可以定义为S=B*C=fold{bcirc(B)unfold(C)}∈Rn1×n4×n3.

由于空间域的卷积运算等于频域的点积运算,根据循环矩阵乘法(即循环卷积)的性质,自然可以利用快速傅立叶变换(FFT)来优化张量积的运算速度.

定义 2.正交张量 (Orthogonal tensor):张量Q∈Rn1×n1×n3是对角的,当且仅当

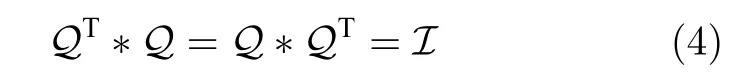
其中,I∈Rn1×n1×n3是单位张量,其满足第一个正面的切片是n1×n1单位矩阵并且其他正面切片的元素全为0.(不失一般性,张量P∈Rn1×n2×n3的转置为n2×n1×n3,其计算过程为先转置P的每一个正面的切片,然后将第2 到n3的正面切片在张量中的顺序颠倒).

定义 3.张量奇异值分解 (t-SVD)[26]:给定一个张量B∈Rn1×n2×n3,t-SVD 可以表示为B=U*S*VT,其中U∈Rn1×n1×n3,V∈Rn2×n2×n3均是对角的,S∈Rn1×n2×n3是f对角.其中,如果一个张量是f对角的,那么其每个正面切片都是对角的.

定义 4.张量多秩 (Tensor multi-rank):张量B∈Rn1×n2×n3的多秩是一个向量p,其第i个元素为Bf的第i正面切片的秩.

基于t-SVD 的张量核范数(t-TNN)定义为

其中Sf可以通过算法1 中的快速傅里叶变换获得.张量多秩被证明是一种有效的范数,是张量多秩的l1范数的最紧凸松弛[27-28].

2 生成式不完整多视图聚类模型

在本节中将首先引入生成模型来估算部分数据的缺失视图,然后在完整数据的基础上进一步引入多秩张量来建模不同视图之间潜在的高阶相关性.

所提算法是基于子空间聚类的,对于高维数据,由于它能够恢复低维数据的子空间结构,因此非常有效.其基本假设是每个数据点可以通过所有数据点的线性组合来重建.它的工作原理是构造一个关系矩阵来编码数据的 “自表示”.给定从多个子空间(簇)采集的N个数据样本X=[x1,···,xN]∈RD×N,子空间聚类的形式可以表示为:

其中L(·,·) 和 Θ (·) 分别表示为数据重建损失和关系矩阵Z的正则项,而λ是平衡这两项的超参数.在获得自表示关系矩阵Z后,可以更进一步得到用来做谱聚类的相似度矩阵

2.1 多视图生成模型

由于最大化似然函数等价于最小化损失 Δ,考虑到缺失的情况,可以获得生成模型部分的以下目标函数:

其中本文使用了线性映射P(v)来表示转换函数.由于数据中可能存在噪声.本方法引入了一个误差项E1.然后将目标函数转换为:

2.2 总体目标函数

实际上,应该计算每个视图中每个样本对之间的相似性.然而,视图不完整的情况导致无法计算完整的相似度矩阵.通过引入隐表示h,可以动态生成缺失的视图,从而使得每个样本具有完整的视图.相应地,利用基于低秩张量约束的子空间聚类来构造样本对之间的关系.相应地,目标函数如下:

2.3 优化

模型的目标函数中存在多个变量块,无法保证对整体变量具有凸性,此处采用交替方向最小化策略[31],即通过固定其他变量来交替更新每个变量.因此,优化可以分解为如下多个优化子问题:

H-子问题:固定其他变量后,通过最小化以下目标来更新H:

得到与H相关的导数并将其设置为零.可以使用以下规则更新H:

设Z(v)的目标函数的导数为零,最终可以得到如下更新规则:

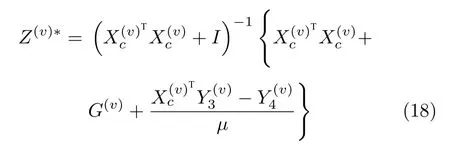
Xc-子问题:变量Xc可以通过以下方式更新:

上面的子问题可以用文献[1]中的引理4.1 来解决.

G-子问题:固定其他参数,通过优化如下目标获得更新:

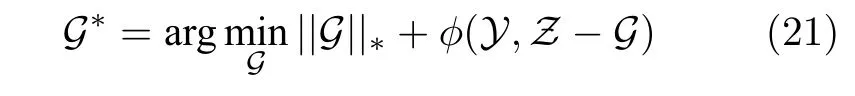
进一步,可转化为以下优化问题

类似于矩阵核范数[16],张量核范数可以基于t-SVD 分解实现优化目标,细节见算法1.

更新乘子项 最后,根据LADMAP[31]算法更新各个乘子系数矩阵:

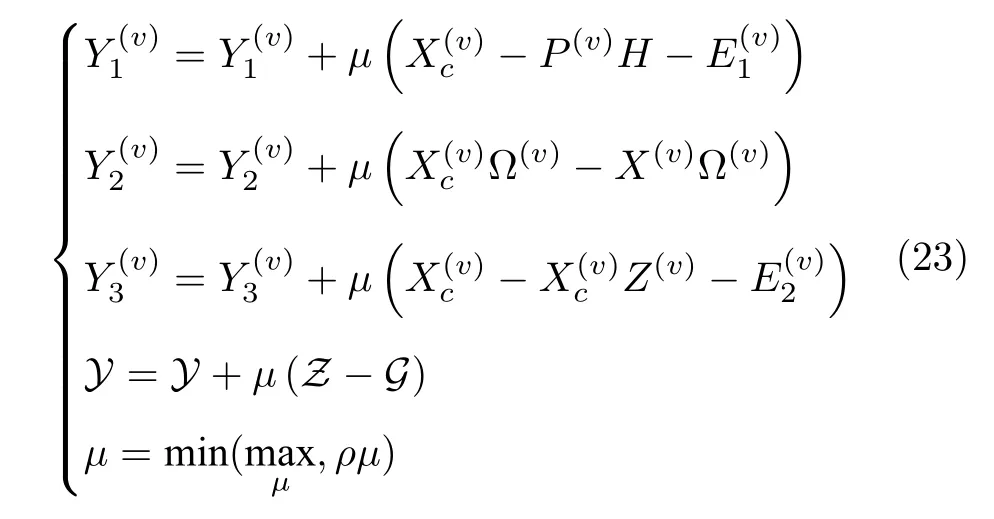
其中,maxμ和ρ分别对应于乘子系数的上限和正系数.

2.4 复杂度分析

所提算法由六个子问题组成.完整的流程如算法2 所示.更新H的复杂度为O(v(k2d+kdn)+k3+k2n),其中v,n,d和k对应视图个数,数据样本数量,多视图特征的平均维数和隐表示的维数.对于更新P,主要的复杂度是矩阵乘法和隐表示矩阵求逆,其复杂度为 O (v(kdn+k2n+k3)).对于更新Z和Xc,主要的复杂度是矩阵求逆,即 O (v(n3)).对于更新E和乘子项系数,主要复杂性是矩阵乘法,即 O (v(kdn+kn2)). 对于G子问题,需要计算n×v×n张量的傅里叶变换和逆变换,及其频域中n次n×v矩阵的SVD 分解,因此该问题的复杂度为O(vn2log2(n)+v2n2).总体上,算法每次迭代更新的复杂度为O(v(k2d+kdn+k2n+k3+n3+kn2+n2log2n+vn2)).因为在多视图情况下,一般有n ≫v,并且考虑谱聚类复杂度以及迭代次数t,整体复杂度为 O (tv(n3+kdn+k2d+k3)).

3 实验

3.1 实验设置

实验主要在如下四个真实数据上进行:

1)Extended YaleB1http://cvc.yale.edu/projects/yalefacesB/yalefacesB.html.这个数据集由38 个人在不同光照下各64 张正面图像构成.与当前相关方法[30]类似,实验中使用前10 类 (每个人的所有图像即为同一类) 的图像,从中提取3 种类型的特征,即有640 个正面人脸图像样本的多视图特征.

2)ORL2http://w.uk.research.att.com/facedatabase.html.ORL 人脸数据集包含40 个人的图像,其中每个人有10 张不同的图像.图像在不同的时间、光照条件、面部表情状态下拍摄,包括3 种特征.

3)COIL20MV3http://w.cs.columbia.edu/CAVE/software/softlib/.Columbia 对象图像库(COIL20MV)数据集包含20 个对象类别,一共1 440张图像,这些图像与2 个视图关联.每个类别包含72 张图像.所有图像都被标准化为 3 2×32 像素阵列,每个像素具有256 灰度级.

4)BBCSport4http://mlg.ucd.ie/datasets/.该数据集由544 篇对应5 个主题的体育新闻文档组成,其中提取了两种不同类型的特征.

在设置的实验中,对于图像数据集,本文均提取图像的如下三种特征:灰度强度、局部二值模式、Garbor 特征.图像的强度特征表示单通道图像像素的值.局部二值模式是描述图像局部特征的算子,其具有灰度不变性和旋转不变性等特点.Gabor 特征可以用来描述图像纹理信息特征.图像的强度特征维度取决于图像的大小,局部二值模式和Garbor 特征的维度分别为3 304 和6 750.对于文本数据集,每个文本被分为两个部分,并且分别用TF-IDF归一化方法提取相应特征[32].

由于所有数据集最初都是完整的,因此,实验中采取随机丢弃视图的策略.本文缺失率定义为,其中指示第i个样本的第v个视图是否存在.在实验中,缺失率从10 %调整到50 %,步长为10 %.为确保实验中样本数目的稳定性,在进行随机丢弃时,保证每个样本至少有一个视图可用.

为了证明所提方法对于不完整多视图数据是有效的,将该方法与几种最新的方法进行比较:联合表示学习与聚类(SRLC)[25],基于t-SVD 的多视图子空间聚类(t-SVD-MSC)[8],不完整多视图聚类(PVC)[23],不完整多模态分组(IMG)[24],多个不完整视图聚类(MIC)[33],双对齐不完整多视图聚类(DAIMC)[34].由于t-SVD-MSC[8]方法不能处理不完整多视图数据集,因此在预处理阶段用该视图的平均值填充缺失的视图.为了保证实验对比的公平性,实验中使用网格搜索方法来调整超参数,并使用ACC 和NMI 聚类度量来评估不同方法的性能在每一个数据集上,分别对每种方法的不同缺失率重复10 次实验,得到其平均性能作为评价.

3.2 实验结果

图2 显示了在不同的缺失率下,不同方法在四个数据集上的聚类性能.结果表明:1)随着缺失率的增加,各种方法的性能都有一定程度的下降.2)在ORL 和BBCsport 数据集上,t-SVD-MSC方法表现出比其他方法更好的性能,表明了低秩约束的有效性,并且可以有效地探索数据的簇结构.在另外两个数据集上,所提方法的实验结果明显优于平均插值的t-SVD-MSC 方法.这是因为在所提模型中,数据插补和聚类可以迭代地相互改进.3) 缺失率在10 %到50 %之间变化过程中,所提出的方法始终优于其他比较方法.特别是对于YaleB 和COIL20MV 数据集,所提方法比其他方法有显著的效果提升.这是因为所提模型可以利用生成模型和高阶张量有效地挖掘不同视图之间的相关性,以保证聚类的性能.

图2 在四个数据集上不同缺失率的准确度(ACC)和归一化互信息(NMI) (平均值 ± 标准差)Fig.2 Results (mean ± std) in terms of accuracy and NMI on four datasets with different missing rate

3.3 模型分析

超参数选择.在实验中,将H的维数设为100,并且提出的模型有两个超参数需要调整λ1和λ2.H的维度是从特定的范围{ 100,200,400,800} 中选择的.在所提的方法中,λ1和λ2是从{10-2,10-1,100,101,102,103}中选择的两个折衷参数.图3 (a)显示了这两个超参数对YaleB 的影响.

收敛性分析.图3 (b)显示了收敛曲线和聚类性能曲线.可以看出,在有限的迭代次数内,收敛曲线下降较快,聚类性能曲线上升较快,证明了所设计的优化方法可以在一定的迭代次数下收敛.

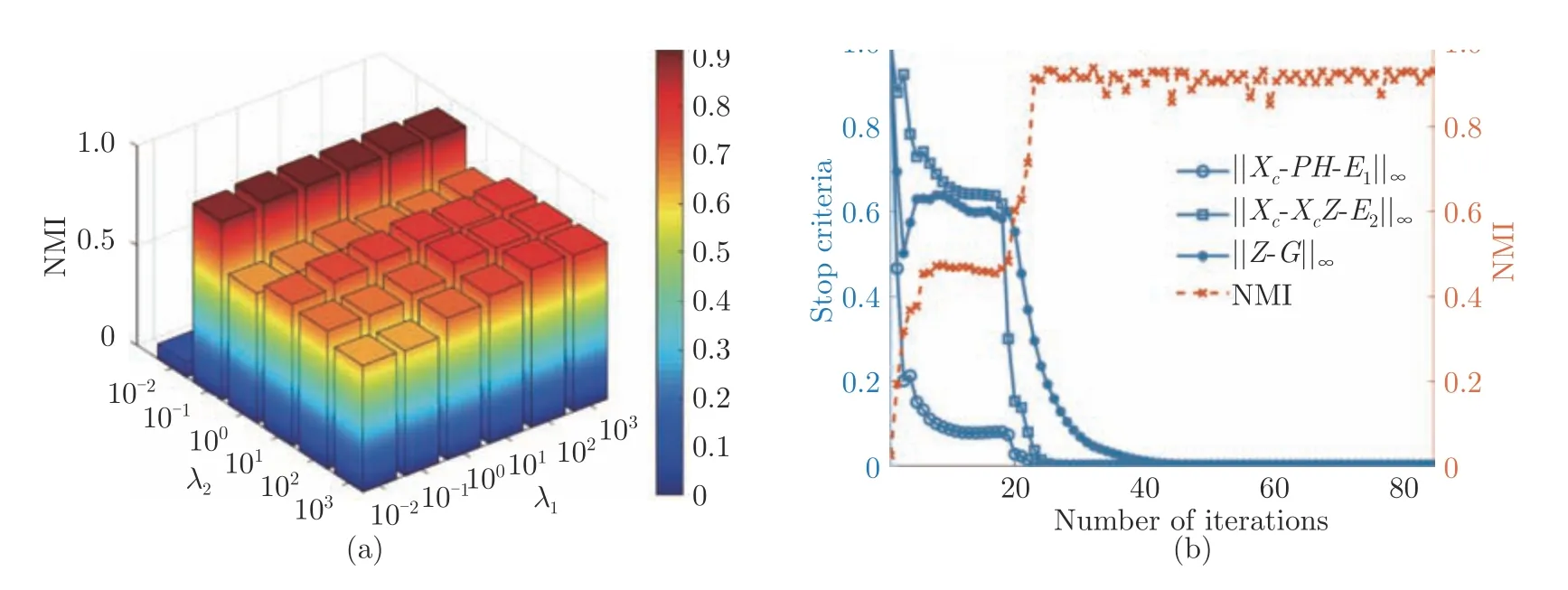
图3 YaleB 数据集上缺失率为10 %时的模型分析:(a) 参数调整对NMI 指标的影响;(b)迭代过程中的收敛条件数值和聚类指数曲线(收敛条件数值已归一化)Fig.3 Model analysis on YaleB with missing rate:10 %:(a) Performence with parameter tuning;(b) Convergence and clustering index curves during iteration (convergence values are normlized)

4 结论

本文提出了一种新颖的不完整多视图聚类模型(GM-PMVC),可以在任意视图缺失的情况下补全缺失并完成子空间聚类.通过隐表示H有效利用所有可用视图信息,有效地编码基于子空间聚类的多视图互补性(即每一个单一视图都来自于完整的隐空间).在融合多视图信息的同时,将各个视图的关系矩阵拼接为三阶张量.由于高阶张量的低秩约束能有效挖掘数据之间的高阶相关性,具体地,基于三阶张量的奇异值分解(t-SVD) (如算法1 所示)的低秩约束既能挖掘各个视图内的低维子空间结构,又能同时保证各个视图关系矩阵之间的一致性.视图的缺失能通过隐表示H补全缺失信息,所提框架同时补全缺失视图和挖掘多视图的高阶相关性,两者相互促进,从而提高聚类效果.由于该框架涉及多个优化变量,本文所使用的增广拉格朗日交替方向最小化(AL-ADM)方法能有效优化含复杂约束项的目标函数,实验证明经过少量迭代次数即能收敛.所提模型具有相对较高的时间复杂度(如表2所示),因此模型在优化效率方面还具有改进空间.本方法在基准数据集上的实验结果与现有的不完整多视图聚类方法相比,验证了GM-PMVC 的有效性,并且在多数验证数据上具有显著的效果提升.

表2 算法运行时间对比(秒)Table 2 Algorithm running time comparison (s)