基于K-means和蚁群算法的配送网络优化问题研究——以南平延平区J速递公司为例

宋李玉，黄建华

（福建林业职业技术学院 经济管理系，福建 南平 353000）

随着电子商务的迅猛发展，快递包裹配送业务量大大增加。福建省南平市延平区地处山区，城市交通线路复杂且客户需求随机无法预测。另一方面，延平区大多数快递企业在网点布局、配送区域划分及配送线路选择等方面带有随意性，普遍依据配送员的主观判断，缺乏科学规划，配送效率并不高。

在配送线路优化方面，国内外提出了贪婪启发式算法、遗传算法、蚁群算法、聚类算法等体系模型求解算法，进行了较为丰富的研究。Lawrence 等[1]（P488-490）首次采用传统遗传算法求解车辆路径调度问题。Clarke等[2]（P568-581）运用贪婪启发式算法研究了VRP问题。Dorrigo等[3]（P73-81）详细阐述了旅行商问题 (Travelling Salesman Problem)，并首创蚁群算法进行求解。Bullnheimer 等[4]（P319-328）把蚁群算法应用于VRP问题研究。张令甜等［5］（P7-12）从南昌市某生鲜电商公司面临的同城生鲜农产品配送线路优化问题入手，建立数学模型，创造性地设计混合遗传算法求解配送线路优化问题。蒋丽等[6]（P244-249）以O2O外卖平台的众包配送路径优化为研究对象，建立带有单侧软时间窗的、需求可延迟的开放式车辆路径优化模型，改进蚁群算法将下一步移动的潜在客户数量作为路径选择的影响因素，对配送路径进行优化。阎宇婷[7]对我国快递行业的区域划分做了详细探究，采用改进FCM聚类算法划分配送范围内的客户点，并通过车辆配载量检验划分结果是否符合目标条件。以上研究方法为本次研究提供了方法支撑。本次研究以J速递公司的延平区配送网络为例，通过K-means聚类法进行配送区域划分，并应用蚁群算法对每一个配送区域内的配送线路进行优化，以此为延平区和福建其他山区城镇快递行业配送线路优化提供参考借鉴。

一、J速递公司配送网络基本情况

J速递公司是一家互联网快递企业，福建代理业务经营范围已覆盖含延平区在内的41个县（市、区），设有5个集包中心，68个营业网点。延平区辖15个乡镇，6个街道办事处，总人口49.5万人，面积2659.66平方公里。目前，J速递公司在延平区设有1个中转站（以T表示）和22个自提点。来自外地的货物通过集包中心分拨，到达T点后再转向22个自提点，见表1。J速递公司在延平区平时的配送包裹量稳定在3500～4000件，若遇“双11”等活动，包裹量可达平时的2.5倍左右，见表2～3。

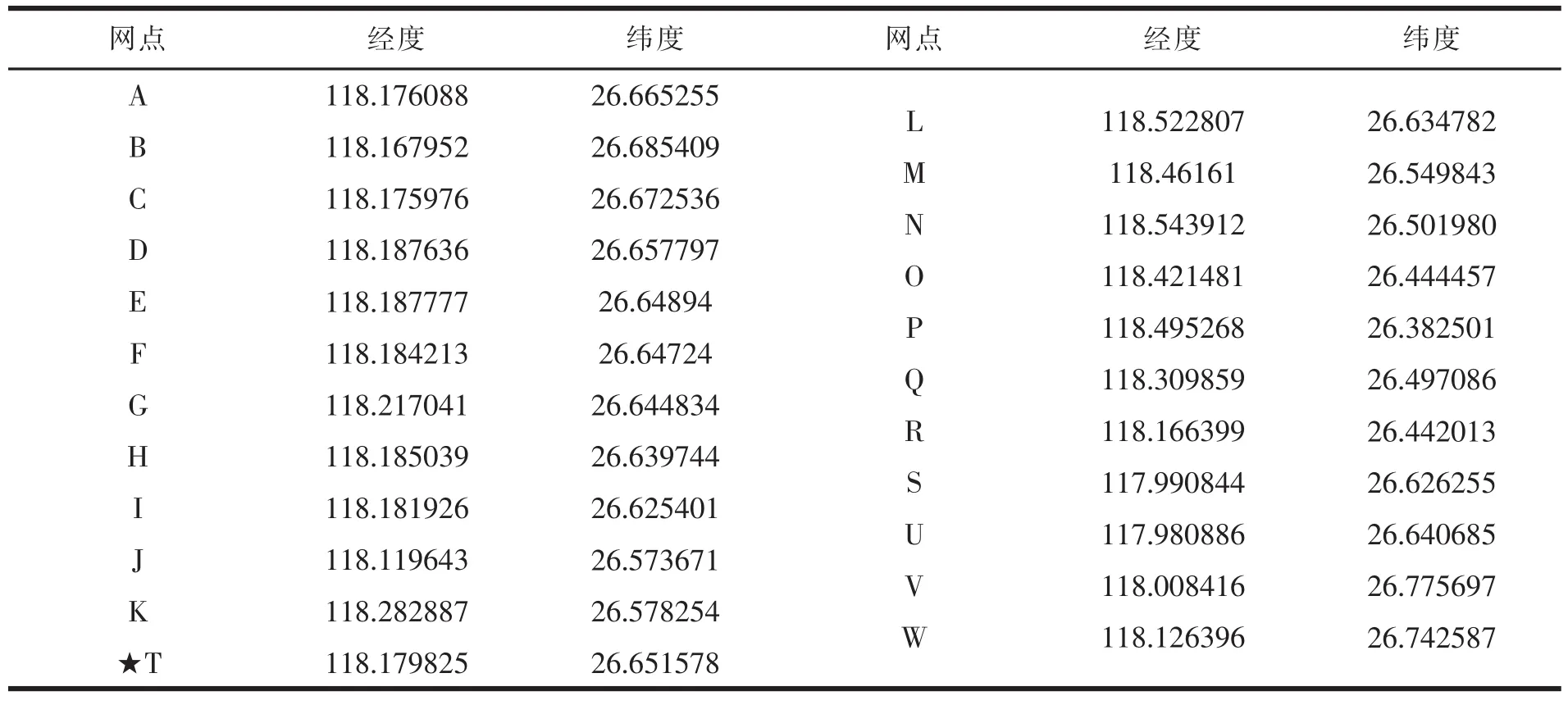
表1 J速递公司中转站及自提点地理坐标

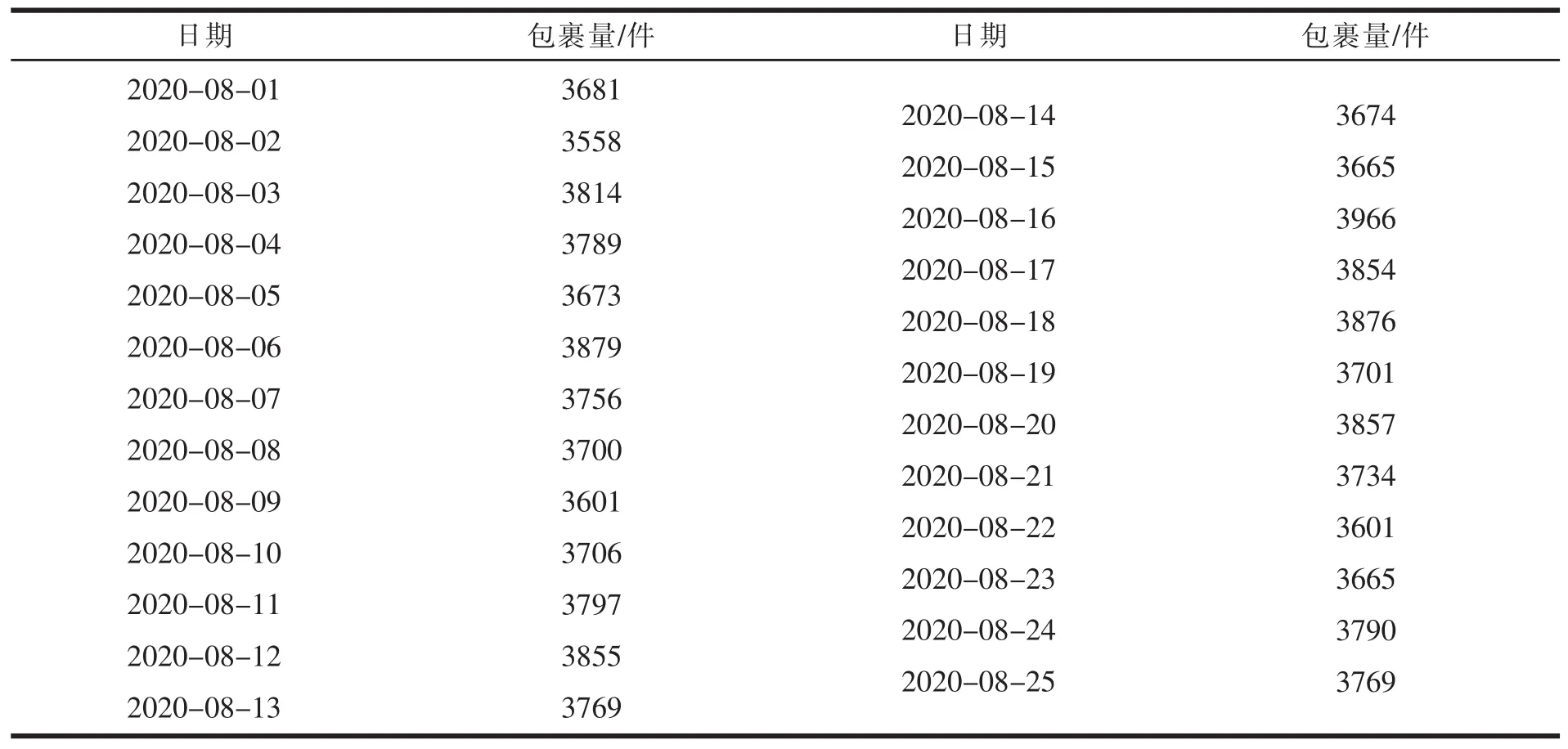
表2 2020年8月份J速递公司在延平区的配送包裹量

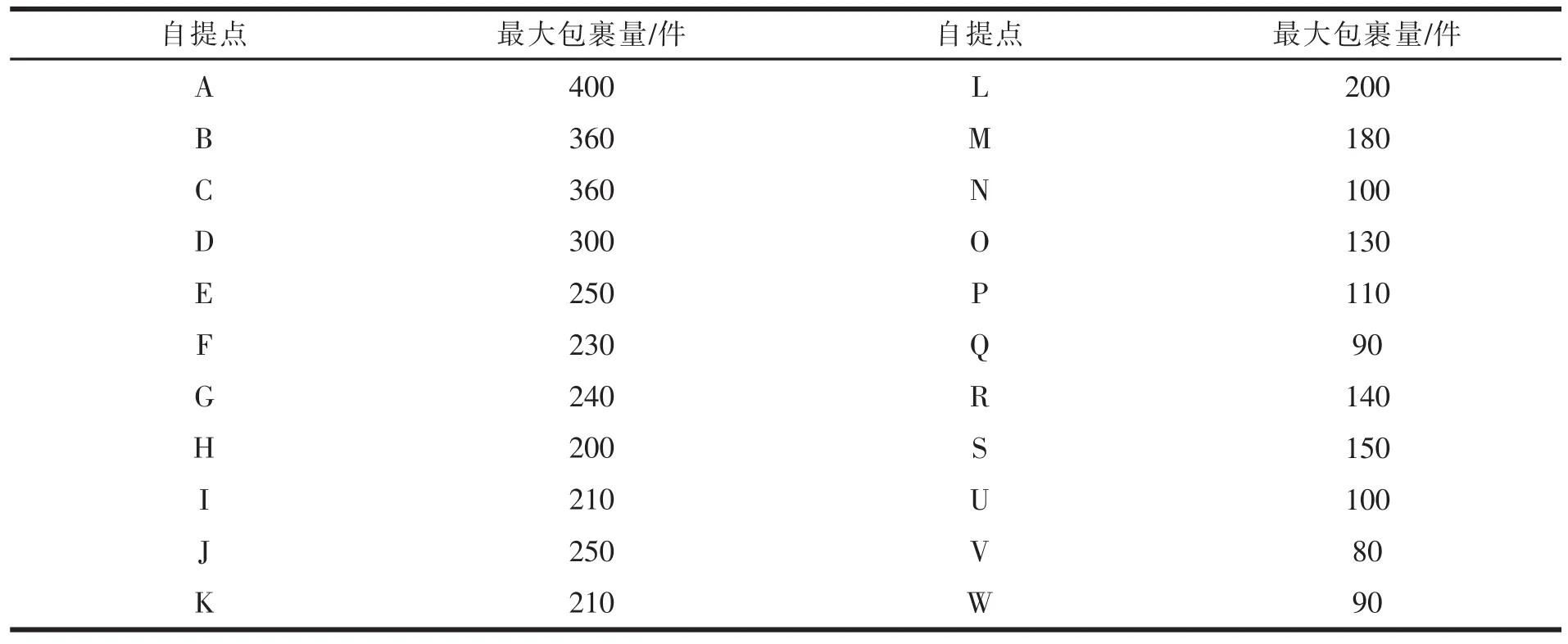
表3 2020年8月份J速递公司在延平区各自提点的最大包裹量

二、基于K-means聚类法划分配送区域实现分区配送

本文通过SPSS中K-均值的功能来实现J速递公司中转站的配送区域划分。K-means聚类分析其本质就是非系统聚类法中的K-均值聚类法。首先将22个自提点的序号、地理坐标输入到SPSS中，以自提点的地理坐标作为标签变量，然后根据李军[8]（P28-34）所提出的确立车辆数公式确定中转站的车辆数：

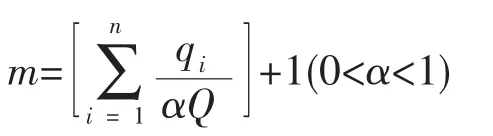
其中，α为参数，是对货物装卸复杂程度和约束条件多少的估计。通常来讲，约束越多，装卸越复杂，则α越小。“[]”表示计算结果取整数。qi表示各个自提点的需求量，Q表示车辆最大配载量。本文α取0.95，车辆最大配载量取1000个单位。结合表3可计算出本文m={5,6}。根据确定的车辆数来确立初始的聚类中心个数，即 k={5,6}。

通过SPSS聚类完成后，需要对每个类别中自提点需求量进行加总，检验各点需求量是否大于车辆的最大配载量。为了保证不出现需求量大于车辆装载量的情况，在每个自提点加入时，都会检验总的载货量是否超标，若超出则该类别会弹出一个牺牲点。牺牲点的选择依据是距离聚类中心最远的样品点。然后，将该点加入到另一个类别中，直至没有牺牲点弹出。具体实施步骤如下：

（1）读取自提点的相关数据：自提点数量、各自提点的需求量以及自提点的地理坐标值。

（2）计算中转站所需车辆数，确定初始聚类中心。

（3）执行分类操作，直至所有自提点被分类完为止。

（4）检验各个区域内自提点的需求量是否超出车辆最大载货量。若超出，执行步骤（5），反之执行步骤（9）。

（5）将距离聚类中心点最远的自提点剔除，直至区域内的各自提点需求量之和符合容量限制标准。

（6）检验是否存在其他类别区域有多余的容量。如果存在，则执行步骤（7），若不存在多余容量的类别，则执行步骤（8）。

（7）在不影响其他类别容量的同时，将被剔除的自提点就近加入该类别，执行步骤（9）。

（8）为中转站增加一辆车服务，即M=m+1,回到步骤（3）。

（9）分类结束。

根据上述步骤运行自提点的聚类过程，当k=5时，运行结果如图1和表4。将上面的运行结果在配送网络图上表示出来，如图2。

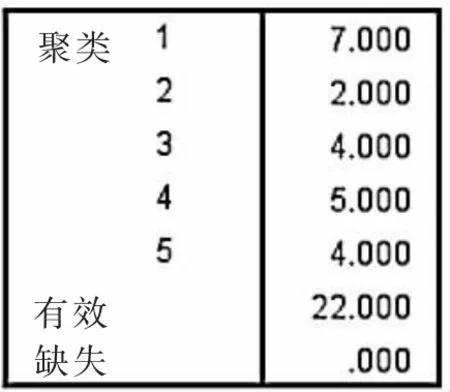
图1 每个聚类中的案例数（k=5）

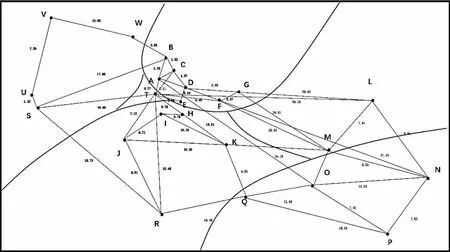
图2 K-means(k=5)聚类分析区域划分图

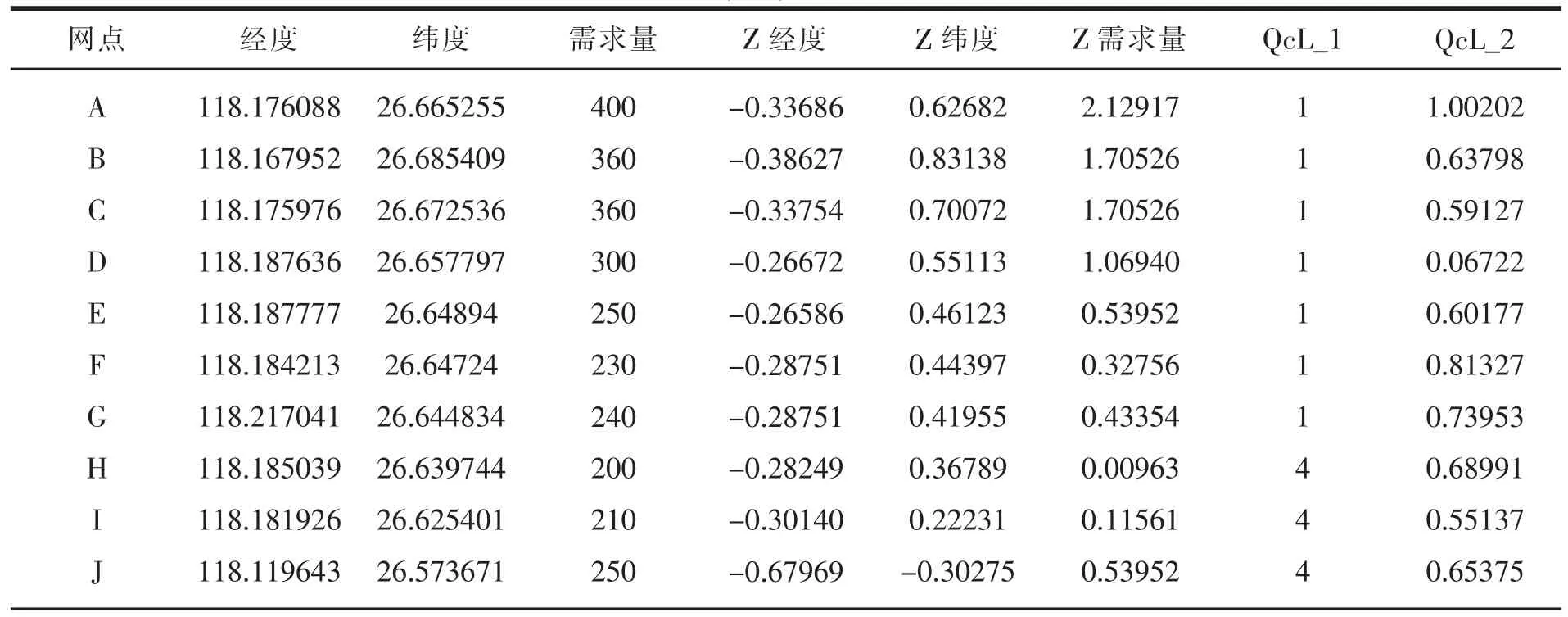
表4 K-means(k=5)聚类分析运行结果

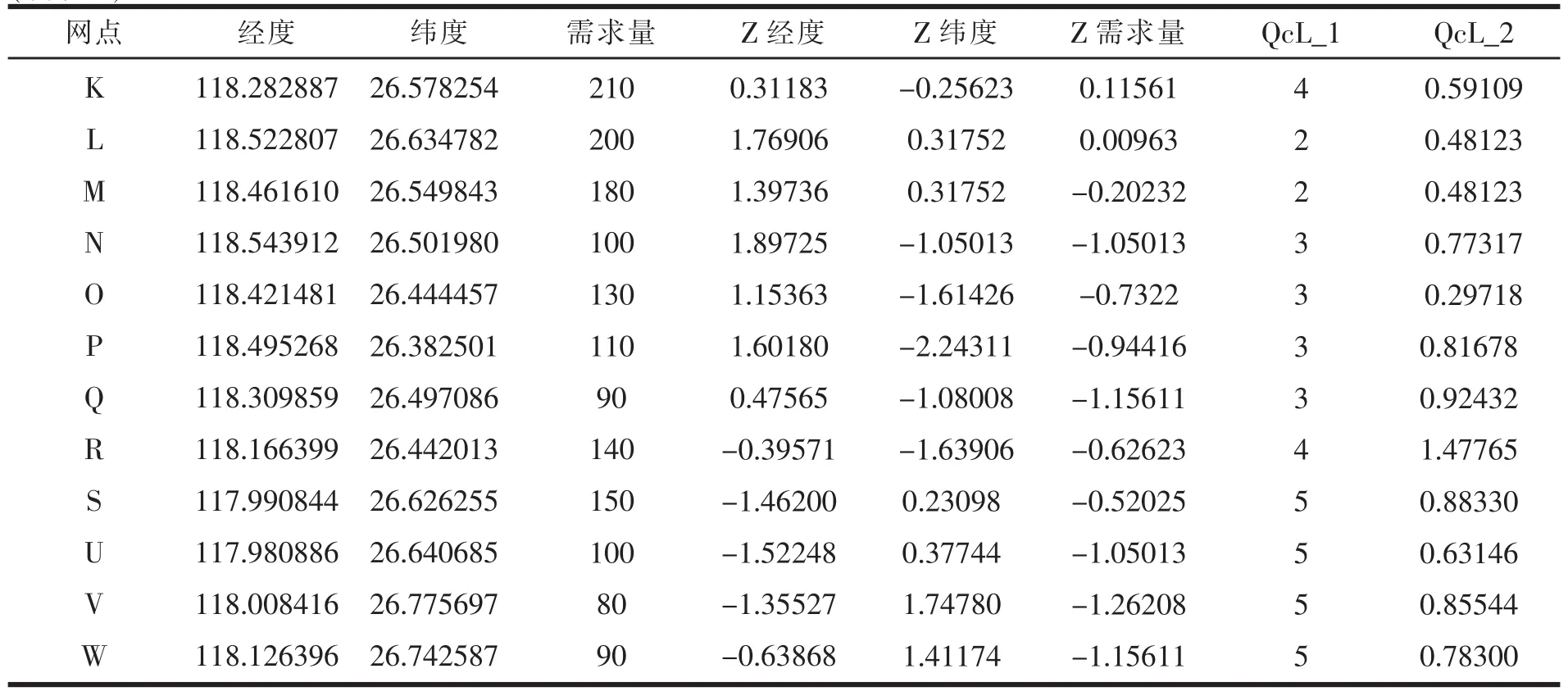
（续表 4）

根据上述区域划分结果，检验各区域内自提点需求量是否超出车辆最大配载量，检查结果如表5。经查，各个区域1和4内自提点的需求量超出车辆最大载货量，k=5聚类方式不合理。将距离聚类中心点最远的自提点剔除，直至区域内各自提点需求量之和符合容量限制标准。在不影响其他类别容量的同时，将被剔除自提点就近加入容量未满的类别，得到修正后聚类结果见表6。当k=6时，运行结果如图3和表7，将结果在配送网络图上表示出来，如图4。根据区域划分结果，检验各区域内自提点需求量是否超出车辆最大配载量，见表8。经查，各区域1和5内自提点的需求量超出车辆最大载货量，k=6的聚类方式需修正。将距离聚类中心点最远的自提点剔除，直至区域内各自提点需求量之和符合容量限制标准。在不影响其他类别容量的同时，将被剔除自提点就近加入容量未满类别，得到修正后聚类结果为表9。

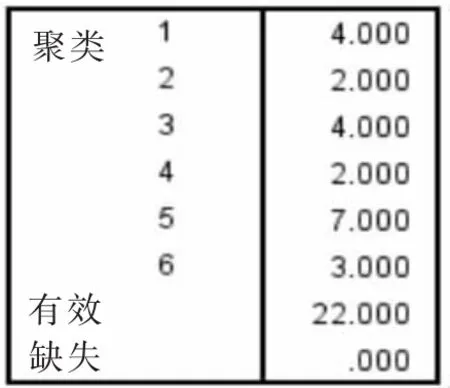
图3 每个聚类中的案例数（k=6）

表5 K-means(k=5)聚类分析结果

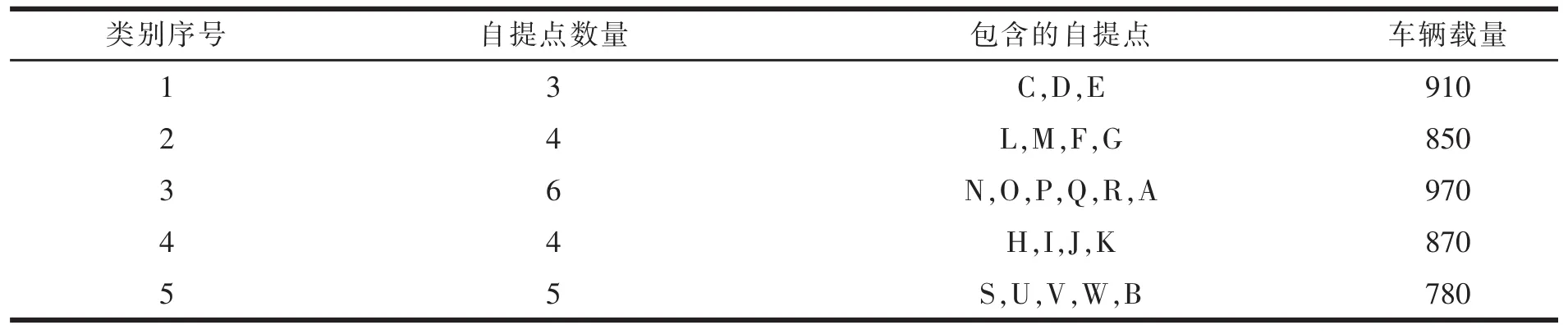
表6 K-means(k=5)修正后的聚类分析结果

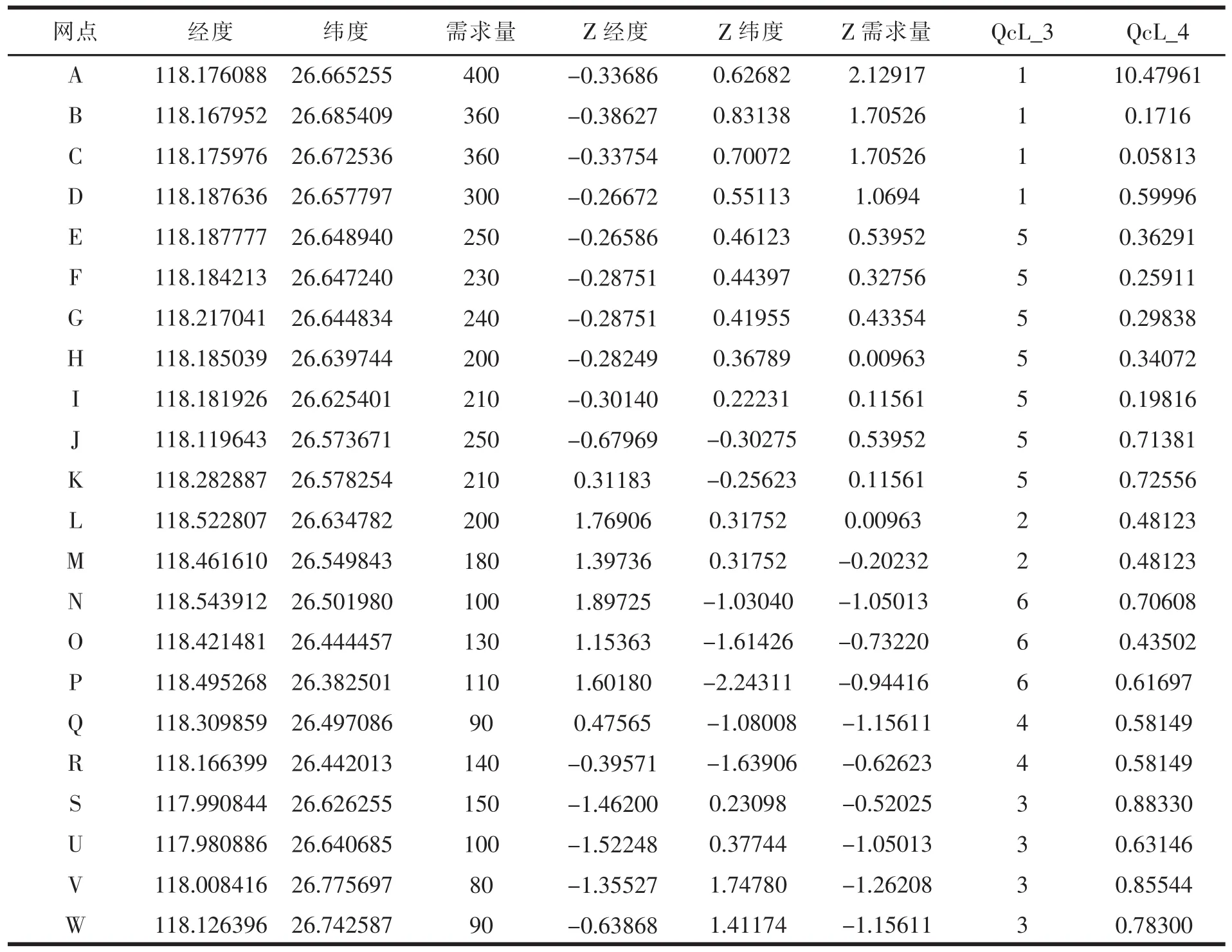
表7 K-means（k=6）聚类分析运行结果

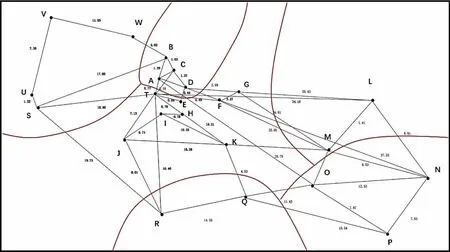
图4 K-means（k=6）聚类分析区域划分图

表8 K-means(k=6)聚类分析结果

表9 K-means(k=6)修正后的聚类分析结果

比较k=5和k=6的聚类情况，k=6时类别6只有三个自提点为K，自提点需求量为340，而车辆最大配载量为1000，则在中转站配送过程中会造成运力浪费，而k=5时则更加均衡，因此，采取聚类数为5的聚类方案，新的配送网络图分区如图5。在运行程序之前，先整理相关数据。根据图5，可计算出区域内各点的最短距离如表 10～14。

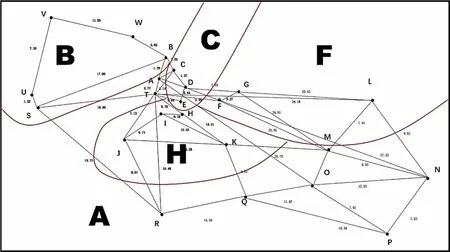
图5 K-means（k=5）新的聚类分析区域划分图

表10 区域C内各点之间的最短距离

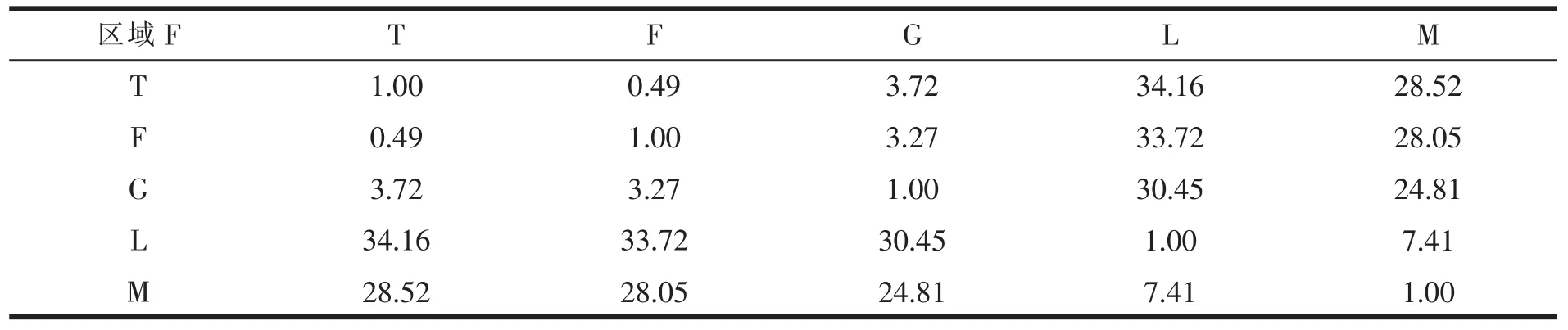
表11 区域F内各点之间的最短距离

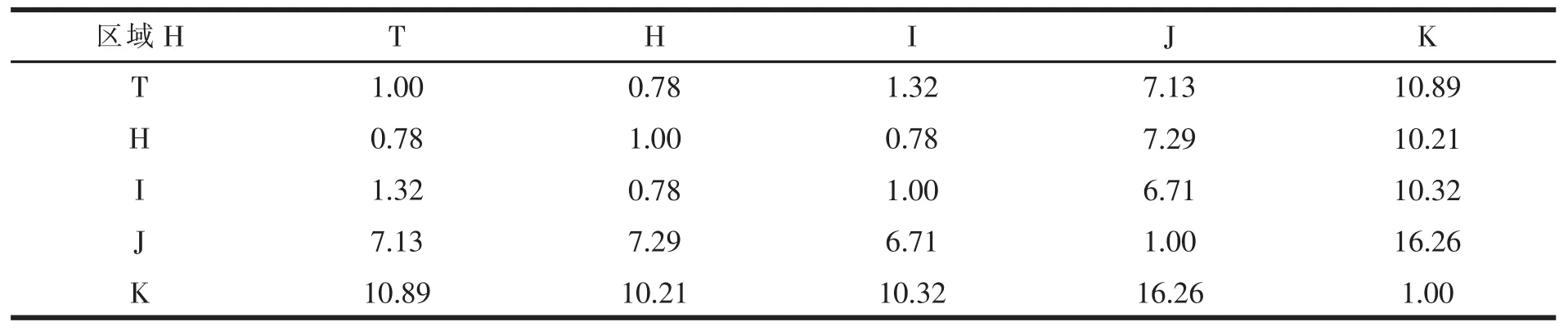
表12 区域H内各点之间的最短距离

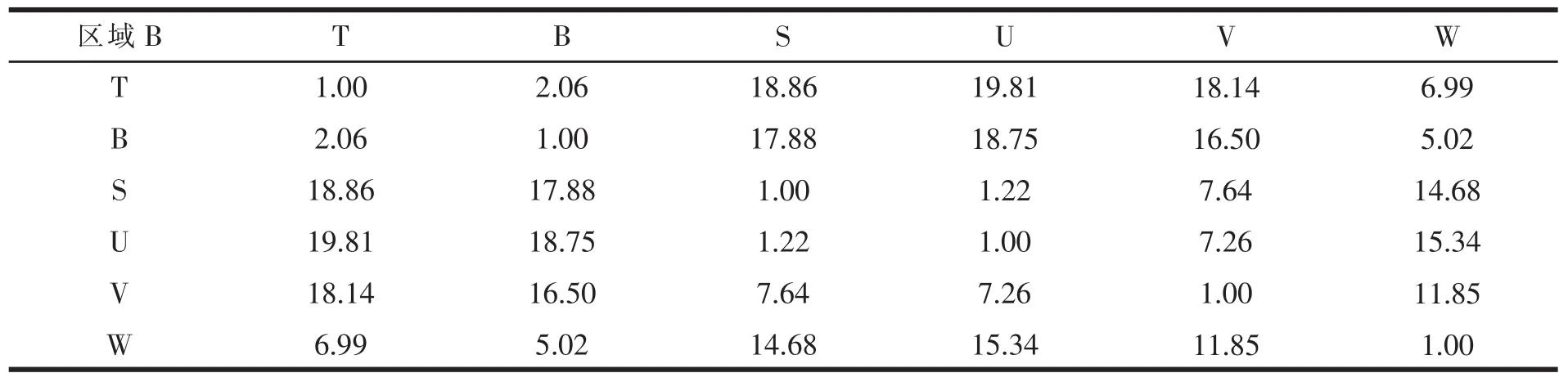
表13 区域B内各点之间的最短距离

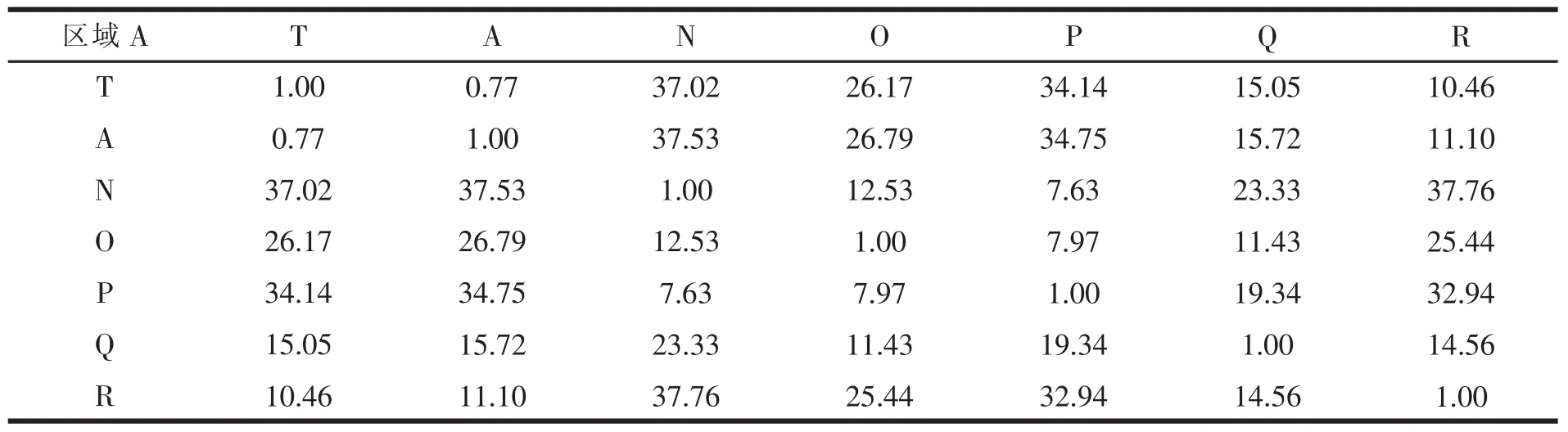
表14 区域A内各点之间的最短距离

三、基于蚁群算法的配送路径优化

为使蚁群算法在求解旅行商问题时，更加贴近延平地区的实际路况。根据各点的最短距离，以中转站T为坐标原点，生成新的坐标图，再将区域内各点的坐标数据输入算法。得到仿真运行结果如图6～10。

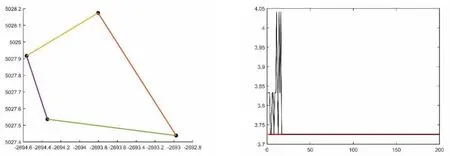
图6 区域C蚁群算法运行结果示意图

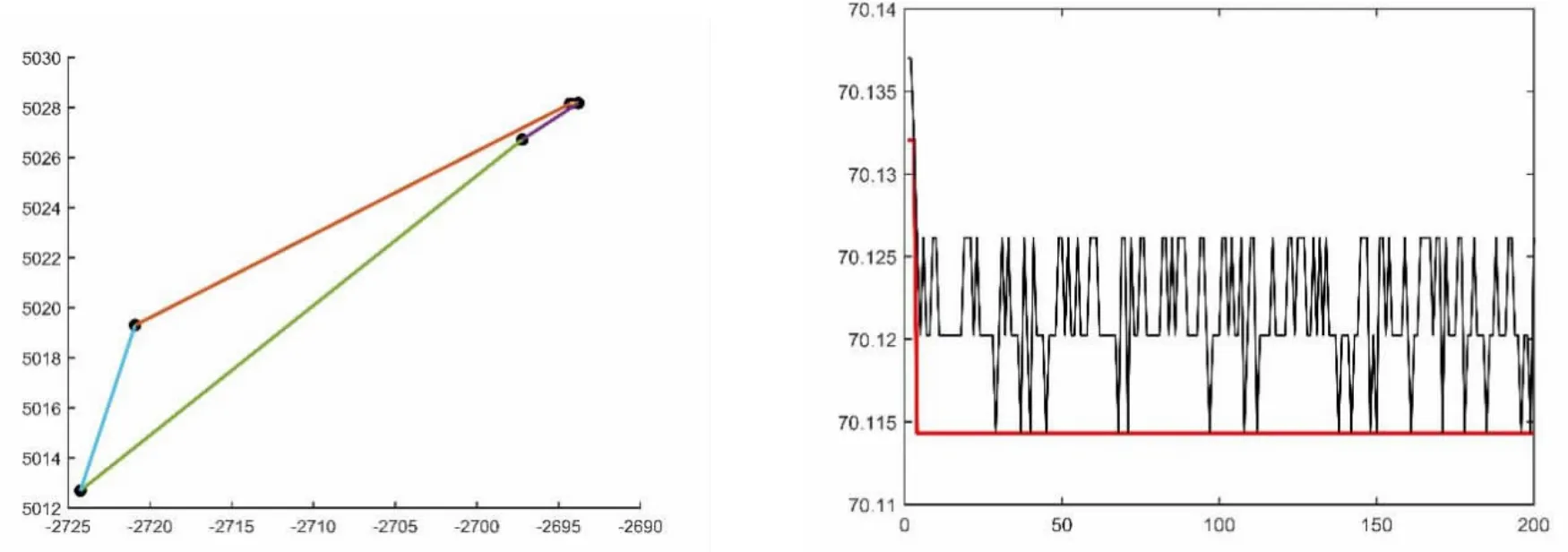
图7 区域F蚁群算法运行结果示意图

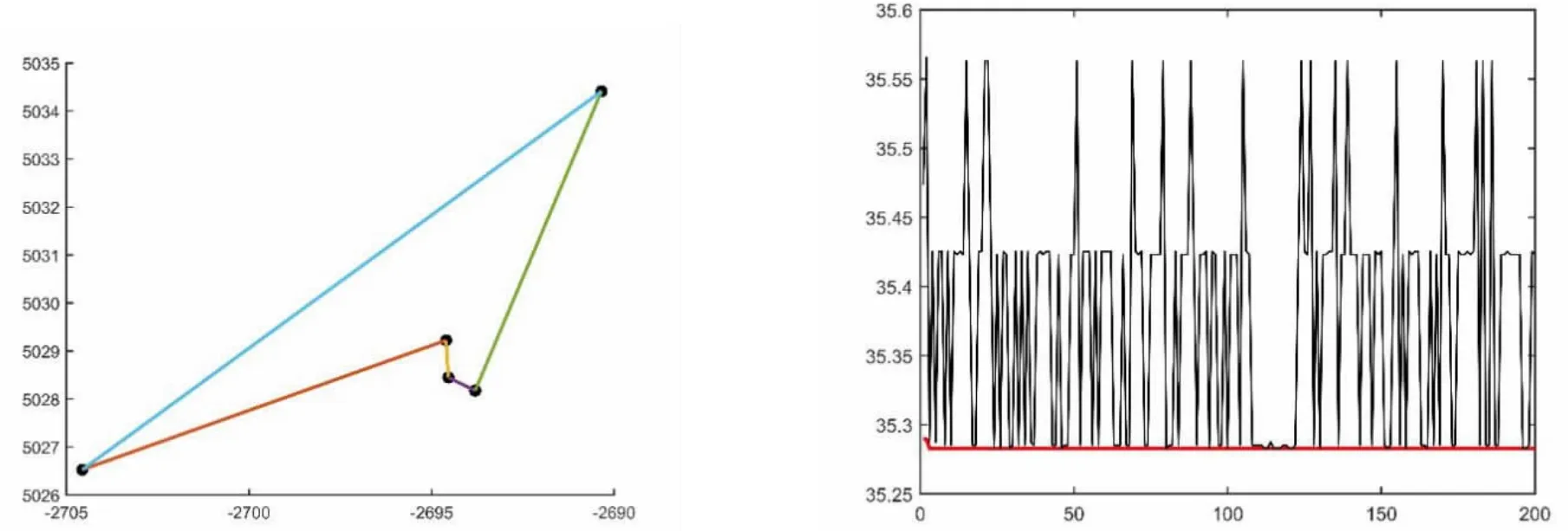
图8 区域H蚁群算法运行结果示意图

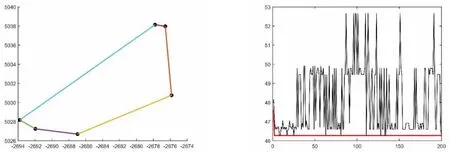
图9 区域B蚁群算法运行结果示意图

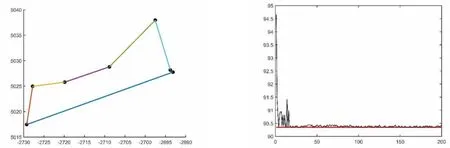
图10 区域A蚁群算法运行结果示意图

由上图可以得出各区域的最优配送轨迹图，并根据区域内各点的最短距离表得到准确的最短路程。若在MATLAB中运行的最短路程与实际的最短路程有偏差，则以实际距离为准。

四、结论

本文通过蚁群算法求解J速递公司延平地区5个区域的最优配送路径，在求解过程中，充分考虑了各点之间的实际道路情况，将两点之间的可达性问题考虑在内。因此，求解的路径更加贴合延平地区的实际道路状况，而不是简单地将各点之间的直线距离作为两个自提点之间的实际距离。

从最优配送路径来看，区域C的最短路径为：T-E-D-C-T，最短路程为 3.726km；区域 F的最短路径为：T-L-M-G-F-T，最短路程为70.138km；区域H的最短路径为：T-J-K-I-HT，最短路程为35.28km；区域B的最短路径为：T-S-U-V-W-B-T，最短路程为46.27km；区域A的最短路径为：T-A-N-P-O-Q-R-T，最短路程为90.36km。通过配送线路优化将多配送员、小批量、散乱的配送方式，变更为少配送员、大批量、系统的配送方式，将为速递企业缩短配送距离、节约配送成本、缩短配送时间，进而提高服务质量。