土石混合体边坡模型随机构建与稳定性分析

贺 勇, 张宗堂,杨期君,张巨峰,李文菁

（1. 长沙市规划勘测设计研究院，长沙 410000； 2. 湖南科技大学岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201； 3. 湖南科技大学资源环境与安全工程学院，湖南 湘潭 411201）

土石混合体（soil rock mixture）是指由具有一定尺寸且强度较高的块石、强度较低的土体及孔隙构成的极端不均匀的松散岩土体，是一种在自然界广泛存在的典型非均质岩土材料[1-5]；Medley也称之为bimrock（block-in-matric rock），意思是“由较细结构的粘结基质与具有岩土工程意义的块体组成”，其中“具有岩土工程意义的块体”表示块体与弱基质之间存在足够的力学对比，并且块体的尺寸分布和体积比例会影响工程规模下的岩体性质[6,7]。在岩土工程领域，土石混合体材料十分常见，例如：川藏公路林芝至八宿段全长427 km范围内，地质灾害的主要物质是土石混合体[8]；浙江省上（虞）三（门）高速公路K92-K95段的边坡为土石混合体，滑坡治理费用高达亿元[9]；攀西地区发生的816个滑坡中，土石混合体边坡就有500个，占61.3%[3,10]。

考虑到这些土石混合体的巨大空间与力学变异性，以往学者们为了简化计算，常常选择使用较弱强度和变形特征好模拟的土壤来开展工作[11-12]，忽略了块体对整体土石混合体强度的贡献。然而，正如许多文献所报道的一样，这种简化可能导致较大的计算误差。也有实践表明，由于土石混合体本身的多向性及不连续性等特征，使用传统的均质岩土材料假定应用于土石混合体岩土构筑物的分析存在明显不足[13]。在目前的研究中缺乏与自然界真实情况符合程度较高的土石混合体模型。

在过去的几十年里，人们进行了大量的研究，以建立正确描述土石混合体特征的系统方法。学者们大都致力于选择适当的强度和变形参数，并进行恰当的数值模拟，以便在复杂地层中正确地开展工程活动。在土石混合体室内试验结果的基础上，一些学者提出了初步的强度准则：假定土石混合体是均匀各向同性的且具有等效的力学性能，则土石混合体的强度可根据其块石含量和土体强度参数确定[14]。还有一些学者分析了在用确定性方法分析非均质地层中边坡稳定性时块石的影响[15]，他们强调了这种土石混合体建模方法产生的特殊结果，与分析均质土体时得到的结果有显著不同。

基于前人的研究成果，本文提出了一种土石混合体的随机生成算法。首先采用数字图像处理来获取自然界的真实块石轮廓，然后通过MATLAB编程来生成具有特定级配和块石含量土石混合体边坡模型。最后分别基于FLAC2D与OPTUM G2对其进行稳定性分析；为了提高结果的统计有效性，对于每种含石量的边坡（含石量0%的边坡除外）进行了5次平行试验，并对两种方法的计算结果进行了对比分析。

1 土石混合体边坡模型的构建

1.1 参数说明

本文旨在探讨含石量对土石混合体边坡稳定性的影响，为此，进行了大量的二维边坡稳定性分析。对于简单的边坡模型，分别采用了有限差分法（FDM）和极限分析有限元法（FELA）对边坡模型进行分析。其中，所有边坡模型的坡度为45°，边坡尺寸如图1所示，级配均一致（图2），但块体含量不同。分别计算了块石含量为0%（均值土体）、20%、40%和60%的土石混合体边坡模型。由于它们是二维模型，块体的面积即被认为等于块石的体积。

图1 边坡尺寸示意图（单位：m）Fig. 1 Schematic diagram of slope size (unit: m)

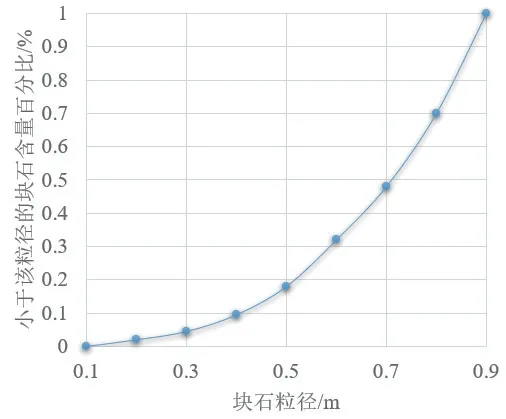
图2 级配曲线Fig. 2 Grading curve

为了考虑块石在空间和尺寸上的变化，作者编写了一个MATLAB程序，用于在边坡区域中生成随机位置和大小的块石颗粒。对于每个给定的级配和含石量，共随机构建了5个不同的边坡模型，即共进行了5次稳定性分析。设置5组平行试验的目的是消除随机误差，以增加结果的可靠性。

此外，还分析了含石量为0%的边坡，以评估地质勘探人员在仅根据土体的强度和变形特性进行设计时可能造成的潜在误差。表1显示了分析中使用的块石和土体参数[1-2,16-18]，两种材料的力学参数取值符合要求（Erock/Ematrix＞2和tanφrock/tanφmatrix＞2）[6,19]。假定它们遵循莫尔-库仑破坏准则，并具有理想弹塑性行为；根据Lindquist和Kalender准则[20]，假设块石为均匀各向同性材料，并通过不同方法对其进行了数值模拟。总共对32个土石混合体边坡分别采用FLAC2D（有限差分法）和OPTUM G2（极限分析有限元）进行了稳定性分析，评估并比较了安全系数。

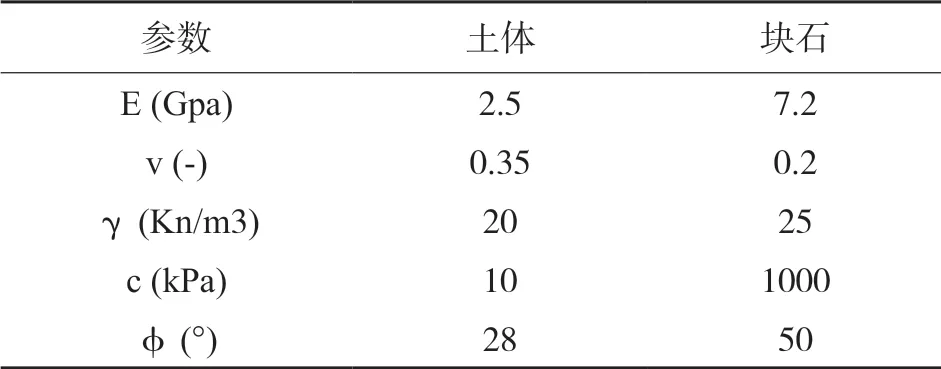
表1 参数取值Table 1 Parameter values

2 边坡模型随机构建

2.1 数字图像处理获取块石颗粒

通过对真实块石颗粒进行拍照并进行数字图像处理，来提取块石颗粒的轮廓坐标。采用数码相机对颗粒进行拍照，相机型号为：佳能600D，高级摄影系统（APS）框架和单镜头反射（SLR）数码相机，1800万像素APS-C CMOS传感器（尺寸：22.3*14.9 mm）和EXPEED 2图像处理芯片，1.6倍镜头转换系数；镜头型号为：EF-S 18-135 mm，67 mm镜头；得到的原始块石照片如图3a所示。首先，利用MATLAB中的rgb2gray函数对块石颗粒的二维照片进行灰度处理（图3b）；然后，利用MATLAB中的fspecial和imfilter函数对图像进行高斯模糊平滑处理（图3c），降低了图像的噪声；使用MATLAB中的im2bw函数对照片进行二值化处理（图3d）后，可以看到二值化处理后颗粒区域为黑色，背景区域为白色；但是颗粒上仍然有一些部分是白色，这是因为颗粒上面的颜色分布不均匀，表面有少量白色区域造成的，不过这并不会影响轮廓的提取。最后，使用MATLAB中的bwboundaries函数搜索边界像素来提取颗粒的轮廓（图3e）。

需要注意的是，轮廓提取后（图3e）得到的颗粒坐标是像素坐标，意味着一个颗粒的轮廓点有几千上万个，这样的块石颗粒直接用于数值计算是不现实的，因为轮廓点太多会造成计算十分耗时。因此，需要对块石的轮廓点进行简化处理。常用的简化方法是等角度随机采样（图3e到图3f），详细过程如图4所示。当采样角度为θ°时，粒子可简化为N（N=360/θ）个点（在本研究中θ=10°，N=36），最终得到简化后的颗粒轮廓如图3f所示。等角度随机采样的详细过程参见文献[21]。

图3 数字图像处理获取块石轮廓Fig. 3 Block stone outline acquired by digital image processing

图4 等角度采样示意图Fig. 4 Schematic diagram of equal angle sampling

2.2 MATLAB编程构建边坡模型

在考虑块石存在的情况下，利用MATLAB编写程序进行蒙特卡罗模拟，根据给定的块石含量和级配曲线，在边坡区域内生成任意直径和位置的真实块石颗粒。对于每个不同的含石量（仅20%、40%和60%，因为0%代表均值土体），随机构建了5个土石混合体边坡模型，即为了实现结果的统计有效性，进行了5次稳定性分析。

当计算得到的含石量（计算为所有块体的面积总和除以边坡模型的面积）对应于输入中定义的含石量时，使用“while”循环停止提取，允许误差为±2.5%。

为了最大限度地提高代码性能，加快计算速度，块石的放置是根据块石粒径的大小从大到小进行的。MATLAB代码满足的其他要求是：（1）块石不能相互穿透，否则就没有物理意义；（2）块石不能与它们所在的斜坡模型的外部边界相交。实际上，任何交叉点都会导致块体体积的部分损失，从而导致对块石含量的低估，这将与规定的块石含量不符。为了达到这些目的，将两个块石之间以及块石与外部斜坡边界之间的最小距离设置为5 cm。最终构建的土石混合体模型如图5所示（含石量40%，级配如图2所示）。

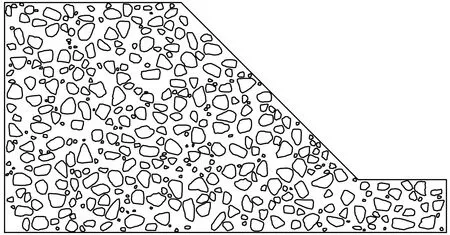
图5 含石量为40%的土石混合体边坡模型示例Fig. 5 Example of soil rock mixture slope model with 40% stone content

MATLAB代码的主要输出结果是一个文本文件，其中包含每个块石的轮廓坐标。为了导入FLAC2D和OPTUM G2，所有MATLAB输出文件都转换成脚本文件，以便在AutoCAD软件中可视化，然后以DXF格式保存。

3 土石混合体边坡模型稳定性分析

分别采用有限差分法(FDM)与极限分析有限元法(FELA)，对含石量为0%（均值土体）、20%、40%和60%的土石混合体进行稳定性分析。除均值土体外，每个含石量随机构建了5个边坡进行分析，共16个边坡，即采用两种方法一共进行了32次稳定性分析。

3.1 有限差分法(FDM)分析

基于软件FLAC2D对土石混合体边坡进行有限差分法分析。首先将前文中得到的DXF格式的边坡模型导入MIDAS GTS中进行网格划分，然后编写一个MIDAS2FLAC2D的接口程序将模型导入到FLAC2D中。分别对不同含石量的边坡采用FLAC2D内置的有限差分强度折减法进行稳定性分析，其计算结果如图6所示，计算所得的安全系数如表2和图7所示。

由图6可以看到，均质土体的塑性区为一条类圆弧滑动带，而土石混合体的塑性区则较为复杂。具体来说，滑动带沿着块石周围进行扩展，呈现出“绕石效应”。这是由于块石的强度相对土体较大，滑动带无法贯穿块石，因此只能绕过块石进行扩展。同时可以看到，随着含石量的增大，边坡的滑动带变得更为破碎和曲折，这与徐文杰等[1]的报导一致。从安全系数计算结果上来看，虽然在相同含石量下，不同组边坡计算所得的安全系数存在一定差异，但是总体上，边坡的安全系数随着含石量的增大而增大，这一点可以在安全系数平均值上（表2和图7）体现出来。同时可以发现，随着含石量的增大，5组边坡的安全系数的标准差也随之增大，说明含石量越大，块石分布的随机性对边坡安全系数的影响越大。

图6 有限差分法（其中一组平行试验）分析结果Fig. 6 Analysis results of finite difference method (one group of parallel tests)

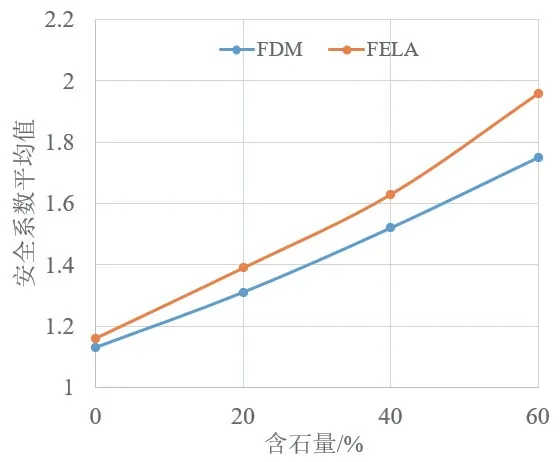
图7 边坡的安全系数平均值Fig. 7 Average safety factor of slope

表2 有限差分法安全系数计算结果Table 2 Calculation results of safety factor by finite difference method

3.2 极限分析有限元(FELA)分析

基于软件OPTUM G2对土石混合体边坡及逆行极限分析有限元分析（取上限解）。将前文中得到的DXF文件导入G2中进行网格划分，然后赋予材料参数（表1）与边界条件（G2中的“标准边界条件”）对不同含石量的土石混合体边坡进行稳定性分析，其计算结果如图8所示，计算所得的安全系数如表3和图7所示。

由图8可以看到，FELA分析得到的边坡的破坏模式与图6中（FDM分析）边坡的破坏模式基本一致，即均质土体的塑性区为一条类圆弧滑动带，而土石混合体的塑性区则较为复杂，且随着含石量的增大，土石混合体边坡的滑动带变得更加破碎。由表3和图7可以看出，边坡的安全系数随含石量的增大而增大，且含石量越大，5组边坡的安全系数的标准差也越大。

表3 极限分析有限元法安全系数计算结果Table 3 Calculation results of safety factor of limit analysis finite element method

图8 极限分析有限元法（其中一组平行试验）分析结果Fig. 8 Analysis results of limit analysis finite element method (one group of parallel tests)

3.3 FDM与FELA的比较

由上述两种计算方式对比可以看到，采用不同方法进行分析的土石混合体边坡的破坏模式相差不大，但是安全系数存在一定的差异。具体来说：FELA方法计算得到的边坡安全系数的平均值会略大于FDM方法计算得到的安全系数的平均值，且差值随着含石量的增大而增大（图7）。同时，对于同一个含石量，FELA计算得到的边坡安全系数的标准差要大于FDM；这是由于在采用FELA方法进行分析时，我们采用的是极限分析有限元的上限解。所以，FELA计算出的结果总是偏安全的，即计算出的边坡安全系数偏大。

4 结论

本文通过数字图像处理获取了自然界真实颗粒的数字化模型，然后基于MATLAB进行特定级配与含石量的土石混合体边坡模型的构建，最后分别采用FDM与FELA方法对不同含石量的土石混合体边坡进行了稳定性分析。结果表明：

（1）采用本文提出的土石混合体随机生成方法，将块石和土体分开考虑进行计算，可有效评估土石混合体边坡稳定性。

（2）含石量对边坡稳定性影响较大，具体表现为：随着含石量的增大，土石混合体边坡的滑动带变得更为破碎和曲折；边坡的安全系数与5组边坡安全系数的标准差随着含石量的增大而增大。

（3）对于土石混合体边坡，FELA方法计算得到的边坡安全系数的平均值大于FDM方法计算的平均值。