Pb-Sr-Nd-Hf同位素参数计算及程序设计

路远发，李文霞

（长江大学资源与环境学院，武汉 430100）

1 前言

Pb、Sr、Nd、Hf同位素都是重稳定同位素，地质过程中不发生同位素分馏，因而其同位素组成只与来源有关而与过程无关。同时，这些稳定同位素也都是放射性成因同位素，其同位素组成与所处地质环境地球化学特征（如U/Pb比、Sm/Nd比和Lu/Hf比等）及地质演化历史有关。由于不同区域、不同构造环境的岩石/矿物地球化学特征及演化历史不同，因此这些同位素组成就成了物质来源与构造环境判别的重要标志，在研究壳幔分离与壳幔相互作用中起着不可替代的作用，倍受广大地学工作者的重视，使之成为当前地球科学的热点之一，相关成果与研究论文不胜枚举。

随着TIMS、LA-MC-ICP-MS、离子探针技术的发展与普及，当前同位素分析测试技术已经有了很大的提高。但是，同位素实验室给出的结果(同位素比值)所反映的地质信息非常有限，更多的信息(参数)需要通过数据处理来提取。因此，同位素数据的精度不仅仅取决于实验室的测试精度，同时也取决于数据处理是否正确。不正确的处理方法当然得不到正确的结果，而用这些不准确、甚至错误的数据来讨论地质作用，就很难保证研究结果的正确性。然而，当前我国地学期刊中的同位素数据处理水平参差不齐，存在不少错误，如个别论文中同位素初始比值比测试值还要高、锶同位素初始比值(校正值)甚至低于BABI值等。当然，这些显而易见的错误是极少数的，更为普遍的是那些难以识别的隐性错误(虽与正确的结果有一定的差异，但不经过验算不易察觉)。究其原因，是目前国内还缺少一个统一的数据处理软件，各位专家多在按自己的理解、用自己的方法处理数据。由于同位素数据处理涉及相对复杂的公式推导，而该学科的成熟与普及时间并不长，许多科学家并未系统学习过同位素地球化学的理论，因而在理解上难免会出现偏差，导致数据处理错误。为此，本文对铅-锶-钕-铪同位素的相关参数以及这些参数的计算公式作一个全面的介绍，在此基础上，给出笔者设计的计算机程序，希望能给国内学者提供一个统一的数据处理平台。

2 计算原理

2.1 铅(Pb)同位素参数

2.1.1 铅同位素组成与增长方程

自然界中铅有8种同位素，其中4种是放射性同位素，4种是稳定同位素。4种放射性铅同位素是210Pb、211Pb、212Pb和214Pb，它们分别是238U、235U、232Th三个衰变系列的中间产物，即铀系中的210Pb和214Pb，锕系中的211Pb和钍系中的212Pb。除210Pb的半衰期较长(T1/2=22.3a)外，其他几个放射性同位素半衰期都很短。这些放射性铅同位素的丰度都很低，相对于稳定的铅同位素可以忽略不计。

铅 的 四 种 稳 定 同 位 素 是204Pb、206Pb、207Pb、208Pb，其中204Pb是非放射成因同位素，自形成至今，其同位素丰度保持不变。206Pb、207Pb、208Pb分别是238U、235U和232Th衰变系列的最终产物，丰度随年龄和U、Th、Pb的含量变化而变化。

相应的206Pb、207Pb、208Pb的增长方程为：

式中下标S代表样品的测定值（可以省略），i代表初始值，λ238代表238U的衰变常数，余类推，t代表矿物(岩石)的形成年龄，下同。

2.1.2 铅同位素主要参数

2.1.2.1 μ值和υ值

定义式为:μ=238U/204Pb，υ=235U/204Pb

由(4)式可知，在一个μ值一定的体系中，从地球形成演化到现在铅的同位素组成应为：

式中a0为地球形成时的206Pb/204Pb比值，下文中的b0和c0则分别代表地球形成时的207Pb/204Pb和208Pb/204Pb比值，T为地球的形成年龄。如果从t时刻开始演化到现在，则有：

由于铅同位素研究的是普通铅，即是t时刻的铅同位素组成，即从地球形成演化到t时刻的铅(并不是从地球形成演化到现在积累的铅)，所以有：

对于普通铅(不含U的矿物、岩石，或虽含U但与铅相比可以忽略不记)来说：

(206Pb/204Pb)t=(206Pb/204Pb)S，因此：

类似公式（9），我们可以得到：

因238U/235U=137.88，因此υ=μ/137.88, υ不具有独立性，完全可以用μ来代替，现在已很少使用。

2.1.2.2 ω值

ω的定义式为：ω=232Th/204Pb

类似于公式(9)，我们可以得到

2.1.2.3 Th/U比值

首先，应该知道，同位素比值是摩尔分数比，而Th/U比值是质量分数比，因此计算过程中要特别注意将U、Th的摩尔分数转换成质量分数w(U)和w(Th)。

由于U主要由235U、238U两个同位素构成，且238U/235U=137.88，其原子量为238.03，由此可得：

Th虽然有6种天然放射性同位素：232Th、228Th、230Th、234Th、227Th和231Th。除232Th外，其余5种为238U、235U和232Th 三个衰变系列的中间产物。由于这些放射性同位素的丰度值非常低，半衰期又十分短，因此一般将232Th的丰度值作为100%。

2.1.2.4 单阶段模式年龄(tCDT)

模式年龄作为成岩-成矿年龄来使用已经不被认可，但仍不失为一个重要的铅同位素参数，如华南的铅锌矿床，成因不同其模式年龄也不同[1]。因此，模式年龄特别是单阶段模式年龄仍是学者们常用的参数之一。

单阶段模式年龄是从地球形成时的原始铅开始，按一定的μ值进行演化到脱离该U-Pb体系(不再接受放射性铅的积累)的年龄。地球原始铅取自Canyon Diablo铁陨石中的陨硫铁(参数参见表1)，因此本文用tCDT表示单阶段模式年龄，以便与两阶段模式年龄相区别。

联立公式(9)和(11)，得

由上式可以看出，只要测得206Pb/204Pb和207Pb/204Pb值，就可以算出模式年龄tCDT。式(16)是一个超越方程，手工是无法获得其解的，但用计算机计算已不再是难题。

2.1.2.5 两阶段模式年龄(tSK)

Stacey 和Kraners[2]提出了Pb同位素两阶段演化模式。他们认为第一阶段从45.7亿年开始至37亿年，在37亿年时地球发生分异事件，从37亿年至现在为第二阶段。

类似于单阶段模式年龄，我们可以获得两阶段模式年龄(tSK)的计算公式如下：

该公式与单阶段模式年龄公式基本一致，所不同的是起始时间和初始比值不同，相关参数详见表1。

2.1.2.6 △α、△β、△γ

△α，△β，△γ分 别 代 表206Pb/204Pb和207Pb/204Pb和208Pb/204Pb相对于同时代地幔的相对偏差，是研究铅的来源和构造环境的重要参数[3]，其计算公式如下：

式中右下角标，S为普通铅的测定结果，M为同时期地幔铅。某一时间(t)地幔值可根据现代地幔值(参见表1)，按公式(4)～(6)进行计算。关于年龄t，计算时优先使用给定的年龄值，如果缺少年龄值，则以单阶段模式年龄值代之，如果单阶段模式年龄值＜0，则取t=0Ma，其中以给定年龄的计算结果最为可靠。如果缺少样品的形成年龄，也可大致估计一个年龄值，如已知样品采自燕山早期花岗岩体，可估计年龄160 Ma，可能比使用模式年龄更可靠。

2.1.2.7 V1、V2

铅同位素组成的一大特点就是同时有206Pb/204Pb、207Pb/204Pb、208Pb/204Pb三组同位素比值，转换成相对于同时代地幔铅的千分差为△α、△β和△γ。在普通的直角坐标图中，一次只能使用两个变量。朱炳泉等[3]、常向阳等[4,5]通过拓扑分析，将△α-△β-△γ三维坐标图中的点投影到下列回归平面中：

在该回归平面中△α，△β的投影点的坐标变换为：

将△值回归平面强制通过0点(即地幔源的点)，可得a=0,b=2.0367,c=-6.143

在该回归平面中进一步建立通过源点的新二维直角坐标系(V1，V2)，则新坐标值为[5]：

将常数a、b、c的数值代入到公式(19)和(20)中，可得如下近似计算式：

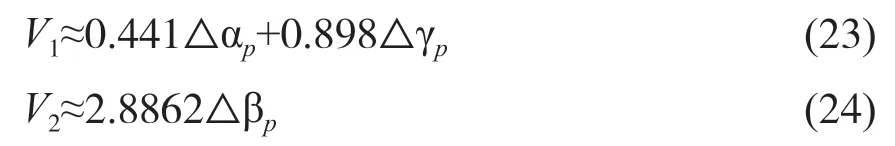
2.1.2.8 初始比值(206Pb/204Pb)i、(206Pb/204Pb)i、(206Pb/204Pb)i

初始比值，也称校正值，是扣除矿物(岩石)形成后放射性成因铅后的铅同位素比值。由公式(4)～(6)可得：

由上式可以看出，计算初始值关键是要求得238U，235U，232Th和204Pb的值。计算步骤如下：

①n(204Pb)值(简作204Pb，下同)的计算

铅的四个同位素之间遵循下列关系

式中p(204Pb)，p(206Pb)，p(207Pb)，p(208Pb)分别代表204Pb，206Pb，207Pb，208Pb在总铅中所占的比例(摩尔分数)，由公式(19)可得：

②235U、238U的计算

③232Th的计算

由上述三步，我们就可以求得样品的235U/204Pb、238U/204Pb和232Th/204Pb，然后根据公式(25)～(27)求得各同位素比值的初始值。至于公式(25)～(27)中的t，一定要用样品形成的年龄而不是模式年龄。

2.2 锶(Sr)同位素参数

2.2.1 Sr同位素组成及87Sr增长方程

自然界Rb有85Rb和87Rb两种同位素，分别占72.15%和27.85%。Sr有88Sr、87Sr、86Sr和84Sr 四个同位素，其所占的比例分别为：82.56%，7.02%，9.86%和0.56%；其中87Sr是放射性成因的，其由母体同位素87Rb通过一个β-衰变而来：

其对应的增长方程为：

2.2.2 Sr同位素组成的主要参数

2.2.2.1 初始比值(87Sr/86Sr)i

由公式(20)可得：

2.2.2.2 εSr

下标UR代表均一地幔库。

2.2.2.3fRb/Sr

该参数反映Rb/Sr比值相对于均一地库的富集与亏损程度，计算公式如下：

2.3 钕(Nd)同位素参数

2.3.1 Nd的同位素组成及143Nd增长方程

自 然 界Nd有142Nd、143Nd、144Nd、145Nd、146Nd、148Nd和150Nd七个同位素。其中144Nd具有天然α衰变，150Nd有β-衰变，但是它们的半衰期都很长(＞1015年)，自地球形成以来衰减的量是当前测试水平无法准确测出，且也是可以忽略不计。144Nd的相对丰度为23.7938%。

自然界Sm有144Sm、147Sm、148Sm、149Sm、150Sm、152Sm和154Sm七个同位素，其中147Sm的相对丰度为14.9957%。147Sm因α衰变引起子体同位素143Nd增长。

其对应的增长方程为

2.3.2 Nd同位素主要参数[6]

2.3.2.1 初始比值(143Nd/144Nd)i

由公式(32)得：

2.3.2.2 模式年龄TCHUR、TDM和T2DM

实测一组Sm-Nd同位素(143Nd/144Nd)S和(147Sm/144Nd)S, 当给定初始值后就可计算公式(33)中的年龄值，即模式年龄。如果以同时代(t)球粒陨石地幔库(CHUR)的值作为样品的初始值，我们会得到相对于球粒陨石地幔库的模式年龄，即TCHUR；如果采用同时代亏损地幔库(DM)的值作为样品的初始值，我们就得到了亏损地幔模式年龄TDM。以下以TCHUR为例：

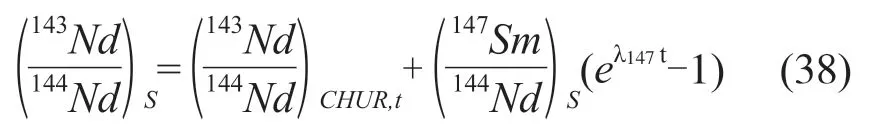
其中：

将(27)代入(26)得：

同理，我们可以得到相对于亏损地幔(DM)的模式年龄:

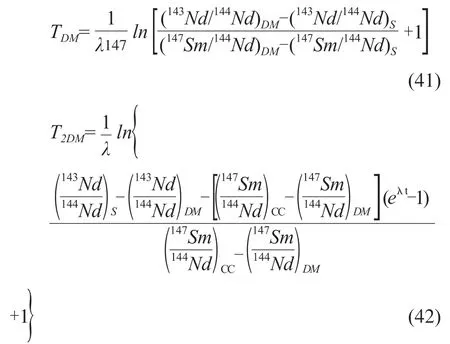
如果先计算出TDM，则T2DM可按下式计算[7]：

式 中：fSa=-1，fCC=,t为部分熔融发生的时间，即第二阶段开始的时间[8-9]，通常用岩体的侵位年龄来表示。

一般来说，对于太古代岩石，由于当时的壳幔还没有充分分离，因此我们通常以球粒陨石地幔库为参照；元古代以后，壳幔已经完全分离，此时的地幔多为亏损地幔，因此常以亏损地幔为参照。需要注意的是球粒陨石地幔库没有单阶段与两阶段之分，是一个理想的均一、稳定的同位素体系。

2.3.2.3 εNd

2.4 Hf同位素参数

2.4.1 Hf的同位素组成及176Hf增长方程

在自然界中Hf有174Hf、176Hf、177Hf、178Hf、179Hf与180Hf 六个同位素，Lu有175Lu和176Lu两个同位素，其中176Lu通过一个β-衰变转变为176Hf：

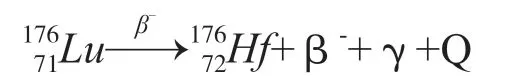
依据放射性衰变方程，可获得Lu-Hf年代学方程：

2.4.2 Hf同位素主要参数[10]

2.4.2.1 初始比值 (176Hf/176Lu)i

由式（45）得：

2.4.2.2 模式年龄(TCHUR、TDM、TDMC)

Hf同位素模式年龄的推导过程与Nd同位素模式年龄是一致的，此处从略。

(注：上述各参数中，上标Hf是为了与Nd同位素的相关参数相区别，单独使用时可不加上标。在文献中很少见到，本文参照Nd的TCHUR计算公式建立了的计算公式，可用于壳幔还没有充分分离的太古代岩石的研究)

2.4.2.3 εHf

2.5 同位素常数

上述许多公式中都使用了各种同位素的常数，表1中汇总了Pb-Sr-Nd-Hf同位素的主要常数。

表1 Pb-Sr-Nd-Hf同位素的主要常数Table 1 Main constants of Pb-Sr-Nd-Hf isotopes

3 程序设计

3.1 Pb-Sr-Nd-Hf同位素参数计算程序简介

Pb-Sr-Nd-Hf同位素参数计算是作者开发的Geokit软件中的一个组成部分[25]。十多年来，在广大用户的支持下，作者先后发布了多个Geokit升级版本，当前版本命名为GeokitPro。该版本的小号以更新的日期命名，如一个完整的版本号Geokit-Pro20210328代表2021年3月28日更新。有关同位素参数计算，在GeokitPro中均集成在“地球化学数据库”模块中。用户可以点击Geokit菜单中的相关菜单项，就可以打开数据处理工作薄，然后根据需要切换需要的工作表(图1)。详细的使用方法请参阅随软件发布的的帮助文件。

表2 两阶段模式年龄(tSK)计算实例Table 2 An Example for two-stage model ages of lead isotopes

图1 地球化学数据库的工作薄的工作表标签Fig. 1 The menu of Geochemical database

进入到工作表后，用户可以在工作表中直接进行相关数据库管理与数据处理工作。由于工作表有很多快速输入功能，也可以使用复制-粘贴的功能，因此录入数据较工作窗口方便得多，数据准备工作可以在表格中进行，用户可以直接在相应的表格中按要求输入相关数据(少量的数据修改也可以在窗口中进行)。如果数据库中已有相关数据，可以直接调入到工作表中，方法是点击相关工作表中第一行左侧的图形(按钮)，弹出相应的工作窗口，在窗口中先选择项目、再选择数据集，选择数据集后，该数据集下的数据就会调入到工作表中。图2是Sr-Nd同位素工作窗口，铅同位素、铪同位素工作窗口的结构与之类似。当在工作表中准备好数据后，点击窗口或工作的按钮“参数计算”，即可完成当前工作表中的相关参数的计算，并将计算结果显示在工作表中。

图2 Sr-Nd同位素数据管理与参数计算窗口Fig. 2 The window of data manage and parameter calculating for Sr-Nd isotopes

3.2 计算实例与结果检验

3.2.1 铅同位素参数

⑴ 输入参数：必需参数 (206Pb/204Pb)S、(207Pb/204Pb)S、(208Pb/204Pb)S（下标S代表样品测试值，以下省略）。

可选参数(计算初始值时为必须)：参考年龄 (t/Ma)，U，Th，Pb含量。

⑵ 输出参数：206Pb/207Pb、tCDT、tSK、μ、ω、Th/U、V1、V2、△α、△β、△γ、(206Pb/204Pb)i、(207Pb/204Pb)i、 (208Pb/204Pb)i。

此外，为保证数据的完整性，在数据库中需要录入样品信息等相关数据（下同）。

不同的作者因研究目的不同，使用的参数也有所不同。因此，这些参数通常不会出现在同一篇论文中。以下我们选择了几篇论文中的数据，分别对这些参数进行验证。

⑶ 计算实例

①模式年龄

模式年龄包括单阶段模式年龄(tCDT)和两阶段模式年龄(tSK)。由式（16）和式（17）可知，两个模式年龄的公式是一样的，只是参数不同。我们利用Stacey and Kramers[2]原文中的前6组数据对本软件进行考核，可以发现，所有计算结果均只在末位存在微小差异，这种差异可能与计算过程中所采用不同的数据精度有关，而不是由计算错误所引起。因此，可以认为本文的计算结果与原作者的计算结果是一致的。本软件除了Stacey and Kramers[2]的两阶段模型外，还设计了用户自定义两阶段模型，用户只需要给出自己样品的第二阶段起始时间和第二阶段的初始值即可。

② V1、V2

由于V1、V2两个参数是在△α、△β、△γ三个参数的基础上完成的，因此验证了V1、V2的正确性也就自然验证了△α、△β、△γ三个参数的正确性。Geokit对V1、V2两参数的计算采用的是公式(21)和(22)。表3中的计算实例数据取该参数建立者的原文[4-5]，由对比可以看出，本文的计算结果与原文是一致的。

表3 V1、V2参数计算实例Table 3 An Example for V1 and V2 of lead isotopes

③ 初始值计算

由于大多数学者在研究铅同位素时多采用矿石铅，不需要进行铅同位素校正，因此在铅同位素研究中，初始值计算并不多。表4中的计算实例数据为秦岭古MORB型岩石的铅同位素组成[26]。作者原文中有两组年龄值，一组是本文引用的MORB形成年龄（1000 Ma），另一组是变质年龄(350 Ma)。从表4可以看出：用本软件的计算结果与原文给出的结果都是一致的。

表4 初始铅计算实例Table 4 An Example for Initial ratios of lead isotopes

我们对高庚等[27]报道的安徽铜陵白芒山辉石闪长岩体的铅同位素数据也进行了验算，结果也是除个别数据在末位有±1的差异外，绝大部分计算结果是一致的。

3.2.2 Sr-Nd同位素参数计算

⑴ 输入参数

必 要 参 数：87Rb/86Sr，87Sr/86Sr，147Sm/144Nd，143Nd/144Nd，t。

选择参数：Rb、Sr、Sm、Nd，当缺失87Rb/86Sr时，Rb、Sr为必须参数，当缺失147Sm/144Nd时，Sm、Nd为必须参数。

⑵ 输出参数

(87Sr/86Sr)i，εSr(0)，εSr(t)，f Rb/Sr，(143Nd/144Nd)i，TDM，T2DM，Tchur，εNd(0)，εNd(t)，fSm/Nd。其中Tchur一般用于壳幔还没有明显分离的太古代岩石。

⑶ 计算实例

表5和表6中的数据为拉萨地块西段中新世查加寺钾质火山岩的Sr-Nd同位素组成[28]，计算时年龄采用24 Ma。限于篇幅，本文只列出其中前6组数据（下列各例相同）。

表5 Sr同位素参数计算实例Table 5 An Example for Sr isotope parameters

表6 Nd同位素参数计算实例Table 6 An Example for Nd isotope parameters

另外，对田世洪等[29]所给青海玉树东莫扎抓铅锌矿床Sr-Nd同位素数据进行验证，本文给出的结果与原文也是一致的。

3.2.3 Hf同位素参数计算

⑴ 输入参数

(176Lu/177Hf)S，(76Hf/177Hf)S，t。此外，样品信息及元素含量不参与计算，不作为计算的输入参数，但为保证数据的完整性，在数据库中需要录入相关信息及数据。

⑵ 输出参数

(176Hf/177Hf)i，TDM，TDMC，TCHUR，εHf(0)，εHf(t)，fLu/Hf。

⑶ 计算实例

表7中的数据为西藏冈底斯东部察隅花岗岩体(CY1-01)锆石部分Hf同位素数据[30]。与原文数据对比，除个别初始值、TDM、TDMC在末位有±1的差异外，其它数值完全一致。

表7 Hf同位素参数计算实例Table 7 An Example for Hf isotope parameters

以上计算实例及其与前人计算结果的对比表明，本软件设计是合理的，计算结果是正确的。

4 结语

许多地质-地球化学研究的最终结论来源于同位素地球化学数据的支持，因此同位素地球化学数据处理的正确与否关系到这些结论的准确与正确性，必须引起有关科学家及相关期刊编辑部的高度重视。

本文系统地给出了Pb-Sr-Nd-Hf各同位素参数的计算公式及其导出过程，在此基础上作者编写了一个计算机软件，并将本软件的数据处理结果与前人的数据处理结果进行了对比，结果证明程序设计是合理的，计算结果是正确的。希望该软件能成为国内学者处理相关数据的工具，避免再出现数据处理错误。