采用定长节点分类窗口的低误码平台LT 编码算法
宋鑫,程乃平,倪淑燕,廖育荣,雷拓峰
(1.航天工程大学研究生院,北京 101416;2.航天工程大学电子与光学工程系,北京 101416)
1 引言
喷泉码[1]最初是针对二进制删除信道(BEC,binary erasure channel)设计的,旨在为大规模数据分发和可靠广播场景提出一种理想的解决方案[2]。以LT 码[3]为代表的喷泉码,具有天然的信道自适应特性,可以灵活地产生任意数量的编码符号。因此,无论信道删除概率多大,发送端总能源源不断地产生编码数据直到译码器恢复出源数据。这使得它非常适合应用于传输视频、音频的广播场景[4]、协作中继场景[5]、水声通信场景[6]和自由空间光通信场景[7]等。
尽管喷泉码最初是面向BEC 进行设计的,但其在加性白高斯噪声(AWGN,additive white Gaussian noise)信道中也具有潜在的应用前景[8-9]。文献[10]研究结果表明,LT 码在二进制对称信道(BSC,binary symmetric channel)和AWGN 信道中存在明显的误码平台。文献[11-14]考虑通过优化校验度分布来改善误码平台。文献[11]给出了一种在二进制输入AWGN(BIAWGN,binary input AWGN)信道中设计LT 码校验度分布的方法,即以最大化LT 码的码率值为目标函数,以校验节点每次迭代输出的消息值递增为约束条件,采用线性规划的方法求解出最优的度分布系数。文献[12]针对极低信噪比条件提出了一种改进的度分布设计方式。文献[13]给出了一种适用于大范围信噪比的度分布函数策略,主要思想是根据信道状态信息(CSI,channel state information)的变化及时调整至最合适的度分布函数以保持足够高的码率效率。文献[14]针对系统LT 码,引入了误比特率(BER,bit error rate)下界作为新的约束条件,实现了以更小的译码开销进入瀑布区的效果。
但是,在BIAWGN 信道中,优化校验度分布函数对降低误码平台的效果有限,特别是在码长较短时。在利用线性规划方法设计度分布时,往往考虑的都是无限码长和甚高迭代次数时的理想状态。因此,所设计的度分布一般只在码长较长时才能表现出优良的渐进性能,但对中短码长BER 性能的改善效果却十分有限。
针对上述问题,本文暂不考虑优化度分布的问题,而是试图通过改进LT 码的编码算法来提升其BER 性能。文献[15]指出误码平台主要是由不可靠的小度数值信息节点造成的,这些节点没有连接至足够多的校验节点,因此,被成功恢复的概率更低。为此,文献[15]提出了一种改进的编码算法:对信息节点按照度数值大小进行分类,并迫使校验节点优先从度数最小的一类信息节点中选取。这种算法几乎完全消除了小度数值的信息节点,并使几乎所有信息节点具有了相同的度数。文献[16]则将文献[15]的编码思想应用到了不等差错保护场景中,以略微增加译码开销为代价,将最重要比特(MIB,most important bit)的BER 平台降低了将近3 个数量级。文献[17]提出的改进算法在校验节点选择每个信息节点时,都先从所有的信息节点中随机选取T个节点作为一组,然后再从这一组中选择度数最小的信息节点进行连接。需要说明的是,文献[17]的改进算法对BER 性能的提升程度取决于额外引入的参数T,但是没有给出关于该参数的严谨设计方法。相较于文献[17],文献[18]的改进算法则引入了更多的参数,如衡量校验节点度数值大小的参数d*。若当前校验节点的度数大于d*,则将优先连接至小度数值的信息节点;若度数小于d*,则仍从所有的信息节点中随机选取;若度数等于d*,则依据预先给定的权重确定选取方法。仿真结果显示,这几种改进算法在BEC 或者AWGN 信道中都能够使LT码更快地进入BER 瀑布区,并能显著地降低误码平台。
但是这几种改进算法也存在下述问题:1) 没有给出算法所涉及参数的优化设计方法;2) 算法可达的BER 性能不具备可调控性;3) 算法设计中没有考虑信道条件的约束。
针对上述问题,本文设计了一种面向AWGN信道的改进LT 编码算法,主要思想是引入节点分类窗口对编码过程进行直接操控,利用该窗口标记度数值相对较小的信息节点,并强迫这些节点频繁地连接至校验节点,从而使其获得足够可靠的度数值。本文主要工作是建立了最优参数设计模型。首先,分析了移除小度数值信息节点后的LT 码BER性能,并将理论BER 下界作为算法参数的第1 个约束条件。其次,分析了改进算法的收敛性,设计了参数外信息增益损失比(GLR,gain loss ratio),并将最大化GLR 值作为第2 个约束条件。最后,分析了不同算法参数对编码效率和编码复杂度的影响,指出了参数的优先选取原则,并将其作为第3 个约束条件。仿真结果显示,本文的改进算法能够显著地降低LT 码的误码平台,获得了比传统LT 码和文献[15,17]的改进LT 码更优的BER 性能,证明了算法的可行性。
2 误码平台分析及改进的LT 编码算法
2.1 传统LT 码模型
对于传统LT 码,编码器会对K个信息节点v={v1,v2,… ,vK}进行编码,生成N个校验节点c={c1,c2,… ,cN},且N个编码节点与校验节点一一相连。LT 码的Tanner 如图1 所示。
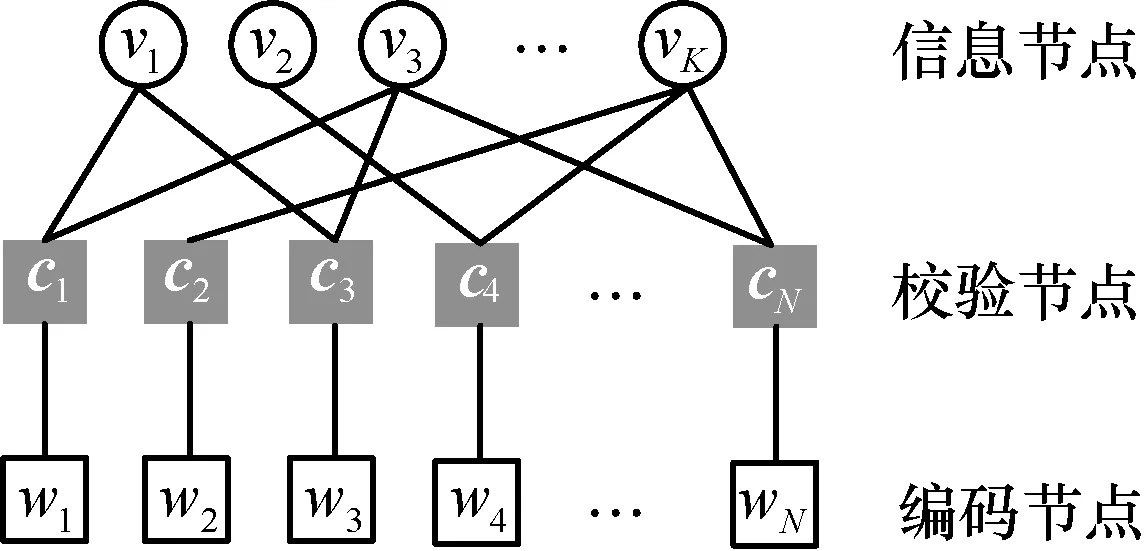
图1 LT 码的Tanner
如图1 所示,定义每个校验节点连接的信息节点的个数为该校验节点的度数值,同理,每个信息节点连接的校验节点的个数为该信息节点的度数值。例如,校验节点c1的度数值为2,信息节点v3的度数值为3。此外,定义校验节点的度分布函数为,其中,Ωj表示度数为j的校验节点出现的概率,dc表示校验节点的最大度数值。定义信息节点度分布为,其中,Λi表示度数为i的信息节点出现的概率,dv表示信息节点的最大度数值。尽管LT 码是无速率码,但仍定义其瞬时码率值为R=。为便于后文分析,此处给出传统LT 码的编码算法,如算法1 所示。
算法1传统LT 码的编码算法
初始化给定K个信息节点v={v1,v2,…,vK},待生成校验节点个数N和校验度分布函数Ω(x),记n=1。
1) 依据度分布函数Ω(x)选择当前校验节点的度数值d。
2) 从K个信息节点中,随机选取d个。
3) 将上述d个信息节点的值进行异或,作为第n个校验节点的值。
4) 令n=n+1。若n<N,则返回步骤1);若n=N,则结束编码,并输出N个校验节点c={c1,c2,… ,cN}。
尽管每个校验节点的度数是依据校验度分布生成的,但可以求得每个校验节点的平均度数为,则每个信息节点的平均度数值为。信息度分布函数的系数Λi为
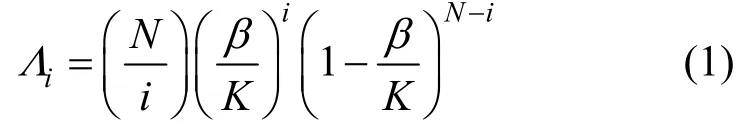
根据文献[11]可知,传统LT 码的信息度分布可以看作以α为均值的泊松分布,即

如图1 所示,在信息节点和校验节点之间任选一条边,定义该条边连接到度数为j的校验节点的概率为ρj,连接到度数为i的信息节点的概率为λi。在此基础上,进一步定义校验节点边的度数分布为,信息节点边的度数分布为λ(x)=。其中,系数ρj和λi的计算方法如下[19]
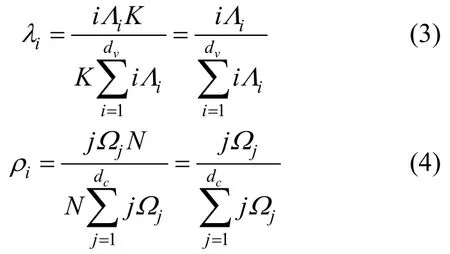
2.2 LT 码的误码平台分析
传统LT 码在生成度数为d的校验节点时,随机选取d个信息节点进行异或,在这种方式下得到的信息节点度分布近似服从泊松分布。然而,从式(1)和式(2)可以看出,即使α足够大,小度数值信息节点(包括度数为0 的节点)存在的概率仍不为零。因此,可以预测,在大量重复实验下,必然还会出现一定数量的小度数值信息节点,这些节点所连接的校验节点很少,在译码过程中往往无法获得足够多的来自校验节点的对数似然比(LLR,log-likelihood ratios)信息,因此,很难对自身的比特值进行正确判决,可靠性较低。
针对这个问题,可以考虑改进编码算法以消除小度数值的信息节点,进而提升LT 码的BER 性能。这一结论可以利用LT 码的BER 下界计算式进行验证。文献[15]指出,在二元输入加性白高斯噪声(BIAWGN,binary input AWGN)信道中,LT 码的平均BER 的下界可表示为
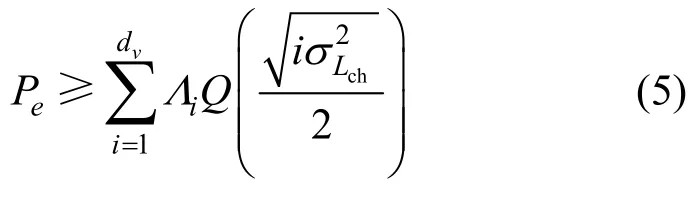
从式(5)可以看出,LT 码的BER 下界只与信息节点的度分布有关,因此,在设计改进的编码算法时,一般只需要考虑信息节点的分布情况即可。为了观察小度数信息节点对LT 码误码平台的影响,分别移除了度数为1,度数为1、2,度数为1、2、3 的信息节点,并计算其各自的BER 下限,结果如图2 所示。仿真采用的码率值为,度分布为文献[20]中K=512 设计的校验度分布,记为Ω1(x)。

图2 移除低度数信息节点后的LT 码BER 下界
从图2 可以看出,移除度数为1、2、3 的信息节点后,信噪比为5 dB 的BER 比传统算法低了将近3 个数量级,这验证了通过改进编码算法降低误码平台的可行性。需要说明的是,图2 中的计算结果是针对码长逼近无限长时的情况,因此,当采用中短码长时,实际的BER 性能可能会有所损耗,且码长越短,与理论BER 下限之间的差距越大。
2.3 改进的LT 编码算法
在实际应用中,为了确保每个信息节点都能正确恢复,并非直接删除小度数值信息节点,往往是通过控制编码过程使每个信息节点都获得足够大的度数值。例如,文献[15-17]中的改进算法会记录并及时更新信息节点的度数值,并强迫小度数值的信息节点优先参与编码进程。但是,上述几种算法也存在2 点不足。1) 无法设立预期可达的BER 标准。换言之,上述文献只是设计了一类优化的信息节点选取规则,当给定编码参数后,算法所生成的信息节点度分布随之确定,即算法的BER 下界随之确定且无法灵活调整。2) 没有考虑信道条件的约束。从式(5)可以看出,LT 码的BER 下界受到信道参数的约束,即与BIAWGN 信道的方差有关。但是,上述改进算法在优化信息度分布时并没有将信道状态信息的影响考虑在内,这可能造成非最优匹配的编码结果。
为了克服上述问题,本文拟设计一种改进的LT编码算法,如算法2 所示。考虑以更直接的控制方式,即引入长度为Tv的节点分类窗口W,用于存储可靠性较低的信息节点,然后强迫窗口内的节点频繁地参与校验节点的生成,直至这些信息节点具备较高的度数值和可靠性,便可暂时地脱离该窗口。具体而言,将编码过程分为2 个阶段。第1 阶段仍然采用传统方式进行,确保所有的信息节点获得初始度数值,以便于开启第2 阶段的编码进程。在第2阶段,节点窗口内存储度数值位于前Tv类的信息节点并动态更新,该编码阶段内生成的校验节点都将只能从此窗口中选取信息节点。假设待生成校验节点总数为N,第1 阶段的校验节点个数为NP,第2阶段的校验节点个数为NS,且满足NP+NS=N。令节点窗口长度为Tv。
算法2改进的LT 编码算法
初始化给定K个信息节点v={v1,v2,…,vK]和校验度分布函数Ω(x),令所有信息节点构成的集合为V,记n=1。
1) 采用算法1 进行编码,生成NP个校验节点,记n=NP。
2) 更新所有信息节点的度数值并进行分类,将度数值位于前Tv类的信息节点存储至窗口W中,记录窗口中的节点个数为ζ。
3) 依据度分布函数Ω(x)生成当前校验节点的度数值d。
4) 如果当前度数值d小于ζ,则从窗口W中随机选取d个信息节点;如果d大于ζ,则选中窗口W中的所有信息节点,并再从集合V中随机选取d-ζ个信息节点。
5) 将选中的d个信息节点进行异或,作为当前校验节点的值。
6) 令n=n+1。若n<N,则返回步骤2);若n=N,则结束编码,并输出N个校验节点c={c1,c2,… ,cN}。
本文所提出的改进算法的优点如下。
1) 度数值相对较小的信息节点能够被优先选取。算法2 引入节点窗口,在第2 阶段的每个校验节点生成之前,将所有可靠性较低,即度数值相对较小的信息节点汇聚在一起,从而使这些节点能够始终优先连接至更多的校验节点。
2) 能够灵活地调整BER 下界。算法2 可以通过调整窗口的长度Tv,调整改进算法能够达到的BER 下限。这可以利用极限思维分析:若Tv足够大,则所有的信息节点都将被置于窗口中且被无差别地选取,改进算法将退化为传统的编码算法,且仍然保持较高的误码平台;若Tv的值较合理,则度数值相对较小的信息节点就能始终被高概率地选取,从而实现更低的误码平台。
需要说明的是,对某个信息节点而言,其是否会位于窗口内并非固定不变的,而是取决于其度数值的相对大小。这意味着,某个度数值足够大的信息节点跳出窗口外后,并非会一直保持在窗口外。随着编码过程的进行,若其度数值又处于前Tv类时,便又将重新回到该窗口内,等待被编码。
2.4 改进算法的复杂度分析
相较于传统算法,本文算法增加了分类信息节点的操作,因而不可避免地增加了算法的复杂度,本节将对其进行详细分析。
传统LT 编码算法的关键步骤包括:1) 依概率选取校验度数d;2) 随机选取d个信息节点;3) 将选中的d个信息节点进行异或。对比算法2 可知,本文算法主要对传统算法的步骤2)进行了改动,而在选取校验度数和求异或值时,与传统算法完全相同。因此,本节重点分析信息节点的选取方式对编码复杂度的影响。
在算法2 中,每个校验节点选取信息节点时,新增操作为节点按度数值大小排序、度数值d和窗口内节点个数大小比较。类似地,文献[15]中的改进算法增加的操作为节点按度数值大小排序、度数值d和每种度数节点个数大小比较。文献[17]的改进算法增加的操作为随机选取T个节点、节点按度数值大小排序、已选信息节点和当前所选信息节点的序号比较。表1 给出了上述几种算法在生成N个校验节点时所产生的新增操作及其次数。

表1 几种算法生成N 个校验节点时的新增操作对比
对3 种改进算法而言,生成每个校验节点时需对信息节点按度数值大小进行排序,这必然会增加编码复杂度。以归并排序算法为例,在本文算法和文献[15]算法中,其平均时间复杂度均为O(KlbK)。因此,本文算法和文献[15]算法复杂度相当,但均高于传统算法。对于文献[17]算法而言,其平均时间复杂度为O(TlbT),其中T为该算法中的参数且T<K。但是,文献[17]算法中的排序、数值比较、随机选取的操作次数均远大于本文算法和文献[15]算法,因此,其总体复杂度相对较高。
3 改进LT 编码算法的分析与设计
3.1 改进算法的收敛性分析
改进算法改变了信息节点的选取方式,但是并不希望过多地增加LT 码的译码复杂度,因此,本节对改进LT 码的收敛性进行分析,并引入参数增益损失比作为算法的约束条件。
LT 码在AWGN 信道中采用置信传播(BP,belief propagation)算法进行迭代译码,分析LT 码译码收敛性常用的工具为外信息传递(EXIT,extrinsic information transfer)图法。参考文献[21],定义单调递增函数J(θ)为

J(θ)具有唯一的反函数θ=J-1(I)。关于J(·)和J-1(·),文献[22]给出了一种近似的计算方法。为便于分析,将LT 码的译码器分为校验节点译码器(CND,check node decoder)和信息节点译码器(IND,information node decoder)。在BIAWGN 信道下,LT码CND 的EXIT 计算式为
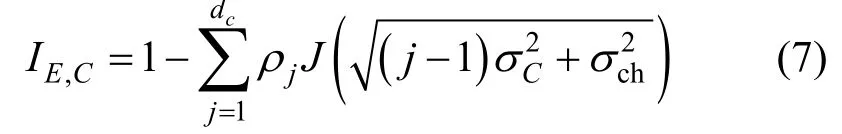
LT 码IND 的EXIT 计算式为

本文改进算法会改变信息节点的度分布,但不改变校验度分布。因此,令改进算法的IND 的EXIT 计算式为
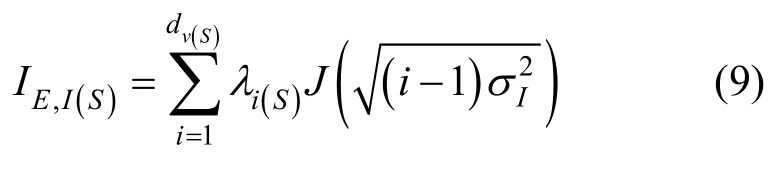
改进算法的CND 的EXIT 计算式仍如式(7)所示。需要说明的是,EXIT 图法常用来寻找固定码率时能够成功译码的临界信噪比,或者是固定信噪比时能够成功译码的临界码率值。但是,对于改进的LT 码,更需要关注的是收敛性的损失或增益情况,即IND 的输入先验信息相同时,改进算法和传统算法的输出外信息的大小对比情况。此处定义LT 码瞬时码率的倒数为R-1,改进算法在第1 阶段产生的校验节点个数与信息个数之比为,第2 阶段校验节点个数与信息节点个数之比为,且满足

为了更直观地观察,在不同窗口长度下进行了仿真。仿真参数为R-1=2,=1,采用校验度分布为Ω1(x),=4 dB。结果如图3 所示。
在图3 中,为了便于观察LT 码的迭代收敛路径,本文参考文献[15],将信息节点的输入先验信息和输出外信息分别置于x轴和y轴;将校验节点的输出外信息和输入先验信息分别置于x轴和y轴。
进一步地,定义CND 曲线和IND 曲线之间的空隙为“译码收敛区”。理论上,如果2 条曲线没有交点,那么当码长K足够长时,译码器总可以经过有限次迭代成功恢复出源信息,图3 中的阶梯即为迭代轨迹。此外,从图3 可以看出,仿真结果与分析结论吻合,即改进算法的CND 曲线与传统算法的CND 曲线会重合,而两者的IND 曲线则存在一个或多个交点。这说明在不同的先验信息IA,I条件下,改进算法和传统算法的输出外信息差值正负不定,可以直观地理解为译码收敛区在不同位置会出现拓宽和压缩的情况。
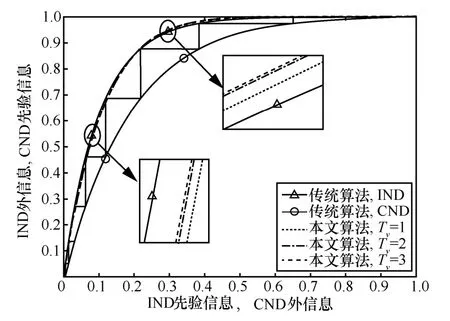
图3 改进算法和传统算法的收敛性对比
若改进IND 曲线位于下方,表明改进算法损失了一定量的外信息,译码收敛区被压缩;若改进IND 曲线位于上方,表明改进算法获得了额外的外信息增益,译码收敛区被拓宽。当信噪比较低或者码率值较小时,压缩现象会更明显,严重时会导致算法无法成功收敛。因此,为了确保译码成功,应合理设计节点窗口长度以确保1) 译码收敛区是打开的;2) IND 曲线的增益最大、损失最小。
3.2 算法参数的约束条件
算法2 引入了额外的参数NP和Tv,为了获得最优的参数组合,本节将分析该组参数对改进算法性能的影响,并给出参数应满足的约束条件。
依据3.1 节的结论,考虑引入参数外信息增益损失比(GLR,gain loss ratio)对算法参数进行设计。令传统算法和改进算法的IND 曲线交点为(x,y),结合式(8)和式(9),可得IND 的外信息损失量为
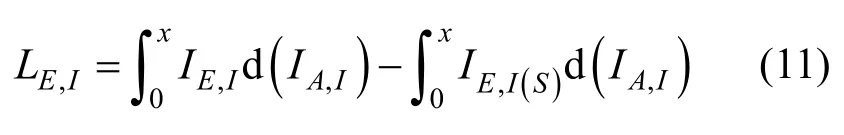
则IND 的外信息增益量为
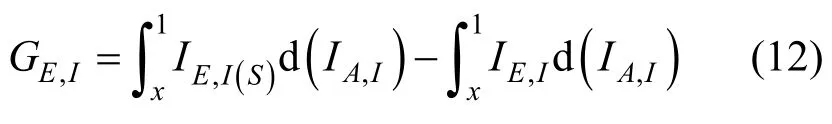
在此基础上,定义GLR 为

改进算法设计的初衷是使LT 码达到足够低的误码平台,但是并不希望过度地压缩译码收敛区,以致出现输出外信息无法收敛至1 的情况。
现将改进算法的参数设计模型总结如下。给定固定信噪比、码率值R以及校验度分布Ω(x)。在区间(0,μ0]中设置D个等间隔μ分布的点,满足μD-1<μD-2< …<μ1<μ0,其中,μ0=floor(R-1),floor 函数表示向下取整函数,并记间隔μ为第1 阶段编码步长。给定初始节点窗口探测范围为[1,α]。需要说明的是,待设计参数为算法2 中的NP和Tv,但为了便于表述,将NP转化为进行设计,这两者是等同的。现希望输出的是最优的参数组合,故引入参数的第1 个约束条件如下。
约束条件1最优参数组合应具有最大的GLR 值。记为
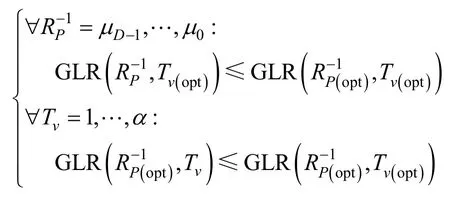
表2 给出了不同参数组合下的GLR 计算结果,其中,校验度分布为Ω1(x),R-1=2。

表2 改进算法在不同参数下的增益损失比
通过表2 的数据可以得出以下结论。
1) 窗口长度Tv的变化会引起GLR值的大范围变动,而参数的变化则对GLR 值的影响有限。这是因为Tv的大小直接决定了小度数值信息节点的消除效果,也影响着信息节点的度分布和IND 曲线的走向,进而决定了GLR 值的大小。
2.2 节指出,直接反映编码结果优劣的是BER 下界,因此,有必要将BER 下界也作为改进算法参数的约束条件之一。此外,考虑到不同的通信场景对BER 的需求不同,应事先给定预期的BER 标准,且该标准可按实际情况进行调整,这也体现了本文改进算法的可控制性、可预测性。
现在,给定期望BER 标准为PE,引入参数的第2 个约束条件如下。
约束条件2最优参数组合的BER下界应高于期望BER。记为
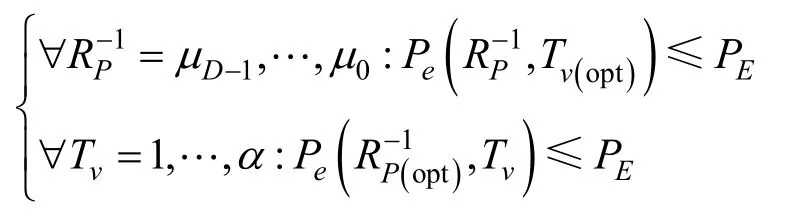
其次,综合约束条件1,参数组合应具有最大GLR值,即满足以下2 点。
1) 对于i∈[1,α]且i≠Tv(opt),j∈(0,μ0]且,可存在某组参数使Pe(i,j)≤PE,但其不可满足GLR (i,j)>GLR
2) 对于i∈[1,α]且i≠Tv(opt),j∈(0,μ0]且,可存在某组参数使增益损失比满足,但其不可满足Pe(i,j)≤PE。
对于上述求解模型,需要说明以下几点。1)计算BER 下界和GLR 值时需要获知信息度分布,为此,本文参考文献[11],采用多次蒙特卡罗仿真的方法,以获取准确的信息度分布。2) 关于步长μ的设置。根据定义,μ=floor(R-1)/D。因此可以按照编码需求取值,如将间隔段数D设置为10。3) 关于节点窗口长度的上限。2.3 节指出,Tv值不宜过大,因此,本文拟采用传统算法的信息节点均值α作为上限。事实上,后续的设计结果也表明,最优的Tv远未达到均值α。
3.3 最优参数的设计方法
3.2 节给出了参数设计的约束条件,即在所有满足BER 标准的组合中,寻找GLR 值最大的一组作为最优。但是,这样的约束条件设计的结果可能存在2 个趋向性:易于向较大Tv值处靠拢、易于向较小值处靠拢。这是因为GLR 值的变化存在一定的规律性,会随着Tv的增大而增大、随着的减小而增大,这点从表2 中容易看出。
但是,在实际应用中,并不希望Tv值过大和值过小,主要有以下2 点原因。
1)Tv值越大,小度数值信息节点的消除效果越差。这是因为节点窗口长度越大,包含的不同度数信息节点越多,而校验节点则是等概率地选取,因此,这就等效于降低了小度数值信息节点被选中的概率。换言之,当Tv值更小时,改进算法能够更准确、更高效地消除小度数值信息节点。为了更直观地展示,图4 给出了不同度数信息节点随校验节点个数的变化情况。仿真参数为=0.2,R-1=2,校验度分布为Ω1(x)。
从图4 可以看出,①Tv值越小,消除效率越高。例如,当Tv=1时,每类信息节点的分布图均比较陡峭;当Tv=6时,信息节点的分布图则比较平缓,且拖尾很长。这说明,Tv值较小,则消除速度越快。②Tv值越小,消除效果越好。例如,当生成相同数目的校验节点时,Tv=1中已经几乎不存在度数为8 的信息节点了;而Tv=6中尚有剩余。
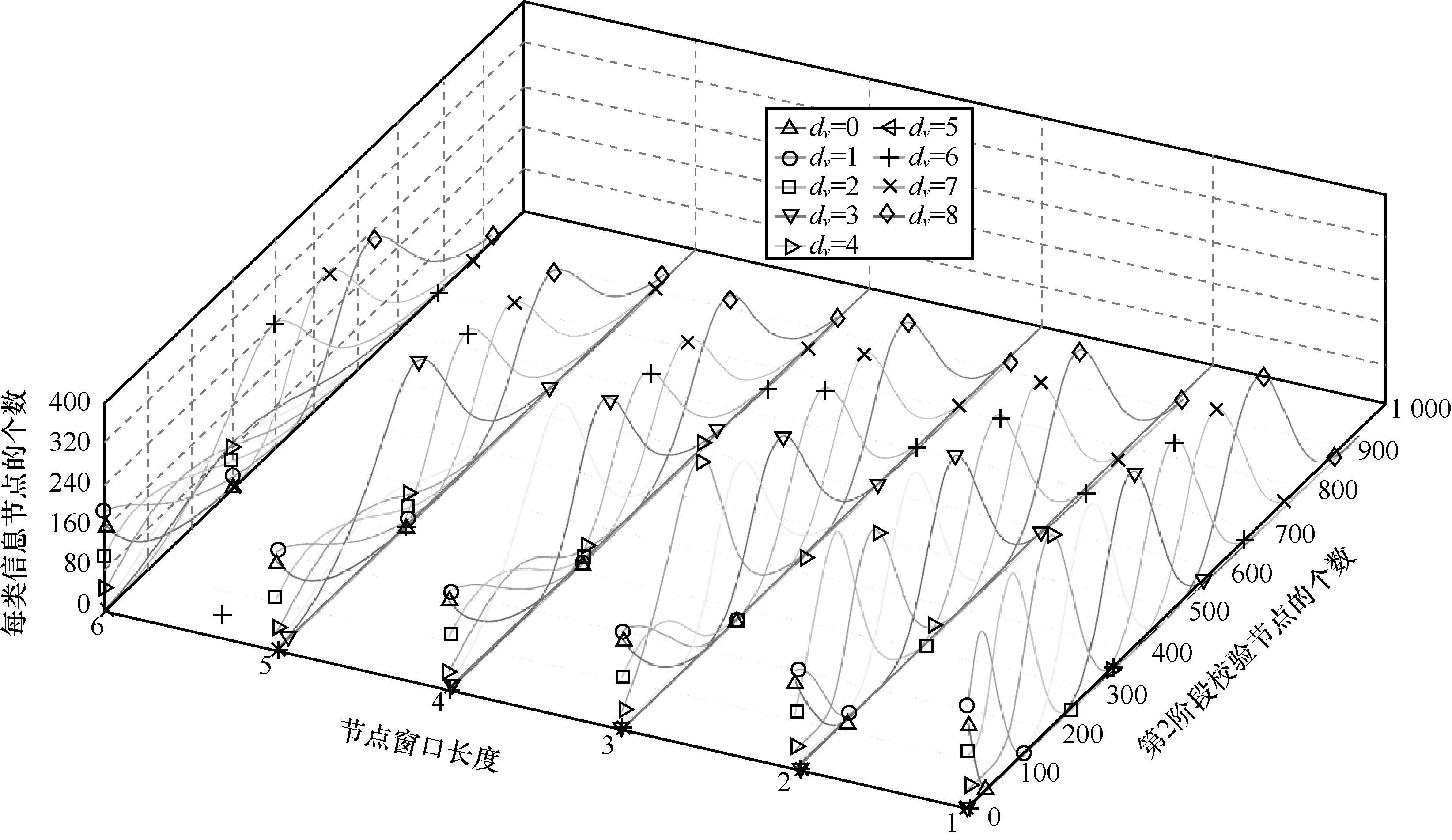
图4 不同种类信息节点随校验节点个数的变化情况
基于上述2 条原因,设计结果实际上应向较小vT值、较大值处靠拢。因此,考虑更改3.2 节中的参数设计约束条件,不再以最大GLR 值作为筛选条件,而是以最大GLR 值为中心,划定可选GLR 范围,并寻找在此范围内的最小Tv值、最大值的组合作为最优组合。为此,引入GLR 半径系数γ(0<γ≤1),并设计参数的第3 个约束条件如下。
约束条件3以最大GLR 值为中心、γGLRmax为半径的范围中,最优参数组合的Tv应最小、应最大。
综上所述,将基于3 个约束条件的算法参数设计模型改写为算法3。按照算法3,给出了一组设计结果示例,如表3 所示。初始条件为采用的校验度分布为Ω1(x),期望BER 为PE=10-9,步长μ=0.2,半径系数γ=0.85。

表3 由算法3 求解出的最优参数组合
算法3求解最优参数的算法
输入期望BER 标准PE,步长μ,窗口长度初始范围[1,α],半径系数γ。初始化m=1
输出最优的组合参数
1) 计算第m个节点窗口长度下,D个不同值对应的BER 下界,记为向量Pm。
2) 筛选出向量Pm中所有小于PE的值,记录其对应的参数组合。计算这些参数组合对应的增益损失比,记为向量GLRm。
3) 若m<α,令m=m+1。重复步骤1)和步骤2),并记录。若m=α,则进行步骤4)。
4) 从记录的向量GLR1,…,GLRm中,寻找出最大的GLR 值,记为GLRmax。在上述向量中,寻找所有GLR 值大于γG LRmax的参数组合,并记录。
5) 从4) 得到的所有组合中,以Tv值优先的原则,筛选出Tv值最小、最大的组合。输出该组合为
需要说明的是,表3 的结果只对所设置的初始条件来说是最优的。而初始条件可以根据不同的通信需求进行调整。例如,若需要更低的BER,则可以将PE的值调得更低一些;若需要更精细的分布,则可以将的值调得更低一些;若对收敛性要求更高,则可将γ调高一些;若希望编码效率更高、复杂度更低,则可将γ调得更小一些。总之,算法3 是综合考虑了BER 性能、收敛性、小度数信息节点消除效率、编码复杂度等因素在内的设计方法。因此,设计结果是一种折中选择,可能不一定具有最低的BER 下界,但具备较稳定、较全面的BER 性能。
4 仿真分析
本节对本文的改进LT 编码算法进行仿真分析,并与其他几种算法进行性能对比。为便于对照,记文献[3]算法为传统算法,文献[15]算法为等度数(ED,equal degree)算法,文献[17]算法为选择连接(CC,connection choice)算法。仿真条件为发送端采用BPSK 调制方式,采用校验度分布Ω1(x),码长K=2 048;接收端采用BP 迭代译码算法,最大迭代次数设置为50 次。所有的结果均通过500 000 次蒙特卡罗仿真得到。
4.1 不同参数组合时的BER 性能
1) 图5 中,固定Tv不变,BER 随着的减小而减小。这是因为,值越小,意味着节点分类窗口能够及早地发挥作用,即在初始时就利用校验节点去主动地连接至小度数值的信息节点;此外,值越小,则第2 阶段的校验节点越多,也就是能够发挥降低误码平台作用的校验节点越多,从而达到更低的BER 下界。
3) 改变算法参数产生的BER 性能变化是可控的。例如图6 中,当=1.8时,Tv为1 时可达最低BER,约为8×10-5,而Tv为5 时则达到最高BER,约为7×10-5,相差不大。如图5 所示,无论Tv是何值,=0.2时均可达到最低BER,=1.8时达到最高BER,但两者均保持在相同的数量级范围内。因此,这验证了3.3 节得出的结论:①可牺牲部分收敛性,以使参数组合向较小Tv值处靠拢;②在对BER 性能要求不高时,可以较大值获取低编码复杂度。
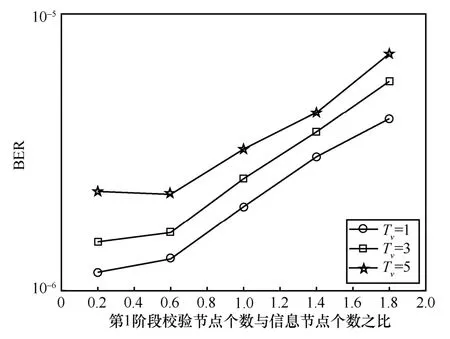
图5 不同节点窗口长度时的BER 性能
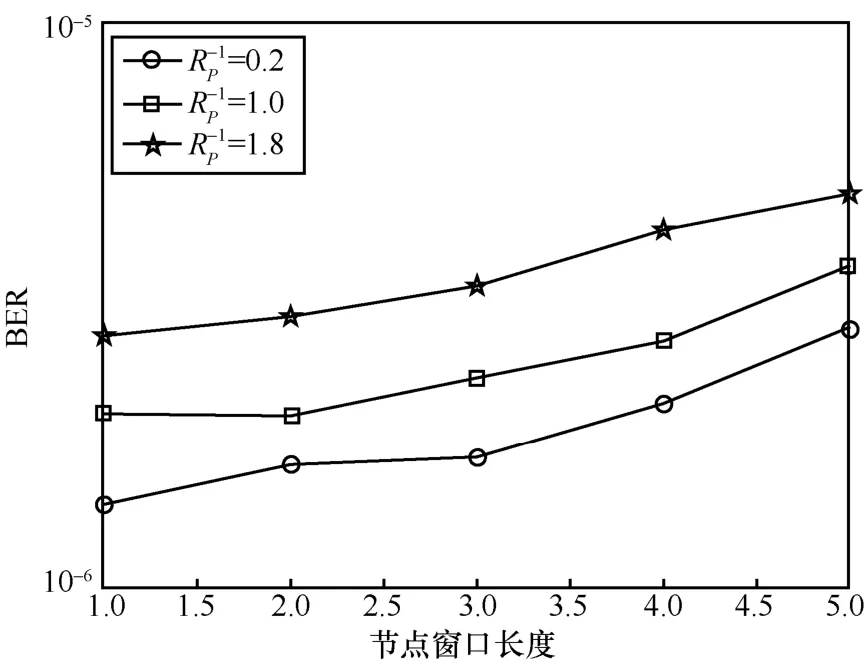
图6 不同值时的BER 性能
4.2 不同信噪比时的BER 性能

图7 =0.2时,不同信噪比下的BER 性能
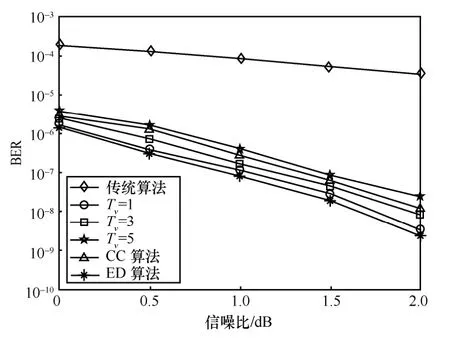
图8 =1.6时,不同信噪比下的BER 性能
1) 改进算法能够实现优于传统算法的BER 性能,达到了预期的设计目的。例如,当=2 dB时,改进算法可将误码平台降低近4 个数量级。此外,当=0 dB 时,改进算法的BER 小于10-5,已经低于传统算法在为2 dB 时的BER。由此,可认为改进算法至少能够获得2 dB 的编码增益,这验证了算法的正确性。
2) 通过优化参数组合,改进算法能够实现优于CC 算法和ED 算法的性能。例如,图7 中,当为0.2、Tv为5 时,改进算法的BER 性能并不优于ED 算法。但是,将Tv调整至1 后,便具有了低于CC 算法和ED 算法的BER 下界。若以10-8为衡量标准,相比CC 算法和ED 算法,改进算法可获得近0.5 dB、0.2 dB 的编码增益,这也体现了本文算法的优势。
3) 通过调整参数组合,能够调控改进算法的BER 下界。改进算法引入了可供调控的参数Tv和,因而具备较强的精准性,且能够降低编码复杂度,这点要优于CC 算法和ED 算法。但是,需要说明的是,仿真结果显示,无论采用何种参数组合,改进算法的BER 性能与理论BER 下界值始终存在一定的差距。例如,当=0.2、Tv为1 时,3 dB处的理论BER 下界值为1.91×10-10,但实际上改进算法的BER 只达到了4.88×10-9。不过,这是受限于编码长度的结果,而不是算法的缺陷。理论BER值是基于无限长码长的计算结果,但受限于编译码复杂度,仿真验证时只能采用中短码长。因此,不仅是改进算法,CC 算法和ED 算法也面临着相同的问题,这实际上是不可避免的折中。总之,仿真结果已经验证了算法的有效性和正确性,这也达到了预期目的。
4.3 不同码率值时的BER 性能

图9 =0.2时,不同码率值下的BER 性能

图10 1.6=时,不同码率值下的BER 性能
1) 当固定信噪比不变时,改进算法依然能够显著地降低误码平台。例如,当R-1=2 时,改进算法远大于传统算法的下界,因此,至少可节省30%的编码开销。
2) 改进算法的BER 性能要优于ED 算法和CC算法。例如,当=0.2、Tv=1时,改进算法的BER 均低于上述2 种算法。此外,尽管改进算法在=1.6时的BER 性能有所降低,但仍具有更低的误码平台。若以ED 算法的最低BER 值为参照,改进算法最多可节省近20%的编码开销,这也体现了改进算法的优势。
5 结束语
针对LT 码在AWGN 信道中存在的严重误码平台问题,本文设计了基于定长节点分类窗口的改进编码算法。为了寻找合理的算法参数组合,以BER性能、收敛性、算法效率等为约束条件建立了参数设计模型。首先,设置参数探测范围,以理论BER下界值为约束条件1,筛选出所有可达标准的参数组合。然后,引入了外信息增益损失比为约束条件2,寻找使GLR 值最大的参数组合,并以此为中心,将半径范围γ内的所有参数组合作为待选。最后,以算法效率和编码复杂度为约束条件3,使设计结果优先向较小节点窗口长度、较大编码开销值处靠拢,进而得出最优参数组合。仿真结果表明,与传统LT 码相比,改进算法最高可将误码平台降低3 个数量级;此外,改进算法也能够实现优于对比算法LT 码的BER 性能。

