基于随机时变图的时间确定性网络路由算法

王鹏，张修社,2，索龙，史可懿

（1.西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071；2.中国电子科技集团公司第二十研究所，陕西 西安 710071)

1 引言

天地一体化信息网络是科技创新2030 重大工程项目，支持全球时空连续通信，具有“全球覆盖、随遇接入、按需服务以及安全可信”的特点。除传统通信业务外，该网络还可对气象、环境与灾害监测、资源勘察、地形测绘等空间任务提供通信服务，并且可提供覆盖全球的宽带接入服务[1]。天地一体化信息网络由天基骨干网、天基接入网以及地面互联网和移动互联网聚合而成。其中，天基网络链路断续连通且网络业务随机占用，网络拓扑和链路时变；地面网络部分由于网络共享，海量业务随机占用，也为链路资源时变的网络。因此，天地一体化网络是典型的时变网络。近年来，随着网络技术的不断发展，电气和电子工程师协会时间敏感网络工作组（IEEE TSN,Institute of Electrical and Electronics Engineers time-sensitive networking）[2]、国际互联网工程任务组确定性网络工作组（IETF DetNet,Internet Engineering Task Force deterministic networking）[3]、第三代合作伙伴计划（3GPP,3rd Generation Partnership Project）[4]纷纷启动了时间确定性网络的研究工作，如何保障业务的确定性时延也成为最近的研究热点。基于此，如何为时变的天地一体化网络提供时间确定性的通信服务[5]，已成为空间信息网络面临的又一挑战。

事实上，国内外学者提出了许多高效的路由算法来降低业务时延。比如互联网开放式最短路径优先协议中的Dijkstra 路由算法[6]，采用贪心策略获取网络中端到端的最短时延；国际空间数据系统咨询委员会（CCSDS,Consultative Committee for Space data Systems）组织提出调度感知包路由（SABR,schedule aware bundle routing）协议，其中所采用的连通图路由（CGR,contact graph routing）策略，可计算时变网络中业务最后1 bit 最早到达目的节点的路径，并且该路由算法已在星上完成了实验[7]。尽管这2 种算法已被广泛认可，路由表计算时未考虑网络资源自身的随机特性。此外，对于多路径路由算法，文献[8]提出了静态网络中基于增广路径方法的端到端最大流算法。与之对应，文献[9]提出了基于存储时间聚合图的时变网络最大流算法，可充分挖掘网络的传输潜力，求解出网络端到端最大流。然而，上述经典的路由方法未充分考虑网络资源随机特性，导致业务端到端时延有长尾效应，网络时延保障能力弱。

为充分说明链路随机性带来的影响，用一个简单的例子来说明。如图1 所示，给定4 个节点的网络，链路权重上的2 个值分别表示链路的速率和满足该速率的最大概率。假设各链路速率的概率分布独立，当大小为100 的数据需从S 传到D，且需要在3 个时间单位内完成传输时，Dijkstra/CGR 算法未考虑链路的随机特性，会选用容量最大的路径S→A→D，如图1(b)所示，则端到端时延为2 个单位时间的概率为0.25。然而，若考虑路径S→B→D，则路径以0.81 的概率保障端到端时延为2.5 个单位时间。显然，若缺乏对S→A→D 随机属性的刻画，若准确获取当概率为0.81 时，选择哪条路径具有更优的时延性能。所以对于节点间链路大部分为无线链路的空间信息网络，如何充分考虑链路的随机性，求解最大概率的时延保障，是亟须求解的问题。

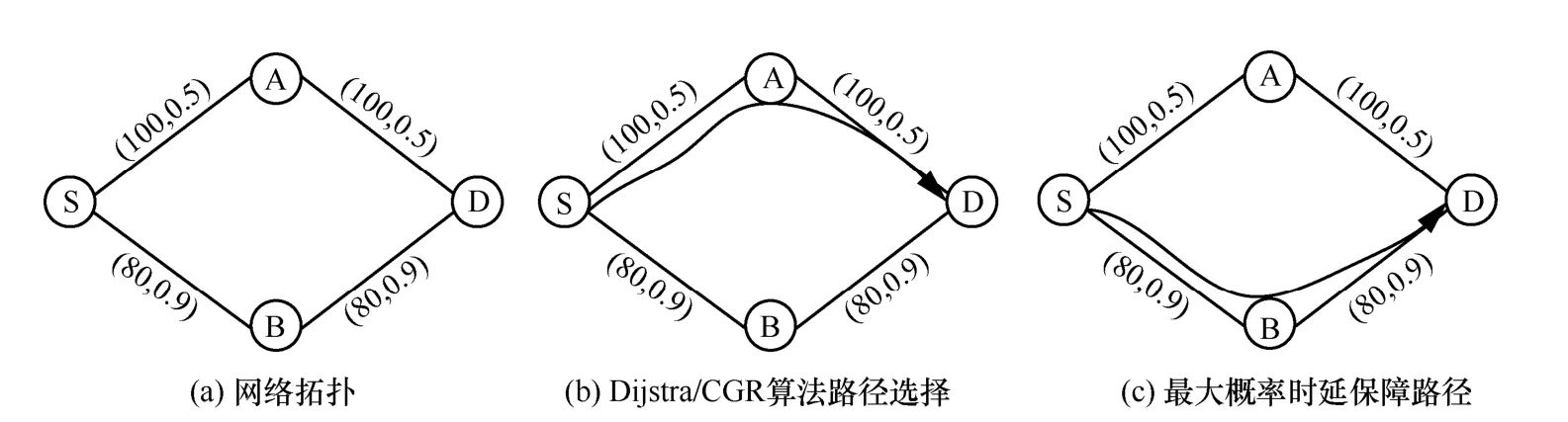
图1 概率图路径选择

实际上，链路的随机性在很多场景中都得到了考虑。文献[10]根据链路对数据分组的成功送达率制定业务在当前节点向每个邻居节点的转发概率，并依据此概率进行路由；文献[11]研究了随机网络给定源汇节点间的连通性确定问题，同样以链路的连通概率为依据进行计算；随机车辆路由问题[12]同样考虑了链路的随机费用特性。上述文献虽然都对链路的随机特性有所考虑，但是主要体现在静态网络链路的概率连通上，未充分考虑时变场景中链路资源的随机特性。

因此，为解决上述问题，首先将时变网络中最大概率时延保障路由计算问题建模为非线性规划问题。为解决该问题，提出了随机时变图模型，对链路可用传输时间的随机特性进行表征。并且，对时变的网络拓扑以及多维资源进行刻画，支持多维资源的联合调度。在此基础上，基于段路由（SR,segment routing）可对不同业务设计不同传输路径的特性，设计了面向业务需求的多项式时间的最大概率时延保障路由算法，给出了样例，详细阐述了该算法的运行过程。最后，证明了算法的最优性并分析了算法的复杂度。

2 问题建模

考虑一个天地一体化网络包含卫星集合S和地面站集合G，其中，卫星集合S={S1,…,SN]包含N颗卫星，地面站集合G={G1,…,GP]包含P个地面站。考虑待传输任务集合M，且M={M1,…,MQ}包含Q个任务。特别地，对于任意任务Mi∈M，采用四元组分别描述生成任务i的卫星Sj、业务量vi、任务释放时间ri、任务截止日期di。由于地面站间被地面高速网络连通，因此所有待传输任务的目的地可以为任意地面站。对于任意任务Mi∈M，目标是从ri开始，在任务截止日期di前将其所有的业务量vi从卫星Sj借助其他卫星的中继传输传回地面站。

针对卫星网络的时变特性，由于卫星飞行轨迹确定，卫星间以及卫星与地面站间的可通信时间窗可以根据轨道模型提前获取。因此，给定时间范围T，可将其拆分成h个小时间段T={T1,…,Th}，使得在每个小时间段内，网络拓扑连接不再发生变化。定义任意小时段Ti∈T时长为|Ti|。

事实上，在任意一个时间段Ti∈T内，由于业务的随机占用，链路被占用的通信时间窗长度服从某个随机分布。因此，在该时段内，剩余的可用时间窗长度同样服从随机分布。假设网络中业务数目足够多，根据大数定律，可假设链路的可用时间窗服从高斯分布，且不同链路之间独立分布。因此可将历史流量信息和路由策略作为输入，利用神经网络[13]、深度学习[14]等人工智能技术，预测未来的链路流量占用情况，进而获取链路各时隙的概率信息。当前工作主要关注在链路随机信息已知的情况下如何构建端到端的确定性时间路由。

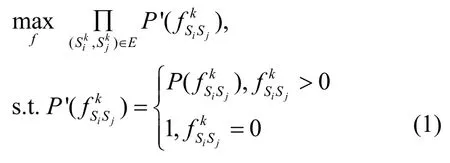
且需满足如下约束。

1) 节点(Sj≠A,D)流守恒约束

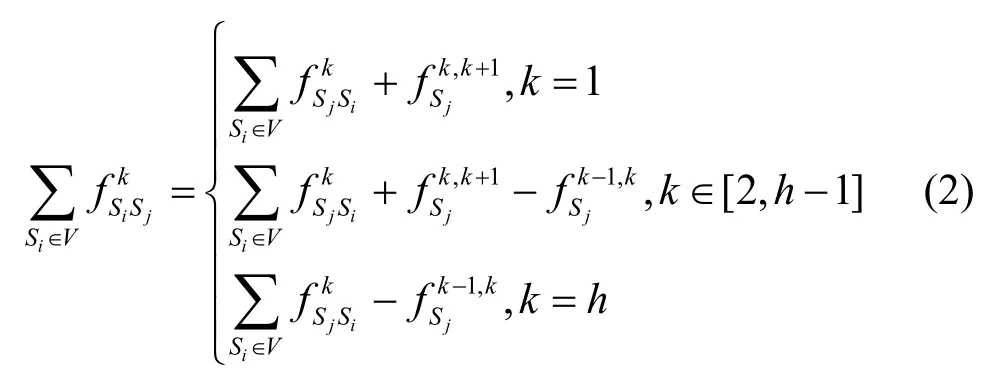
在第一个时段，从传输链路流入Sj的流值的和与从传输链路和存储链路流出Sj的流值的和相等。在任意一个时段（非第一个或最后一个时段），从传输链路和存储链路流入Sj的流值的和与从传输链路和存储链路流出Sj的流值的和相等。在最后一个时段，从传输链路和存储链路流入Sj的流值的和与从传输链路流出Sj的流值相等。因此，将每个时段的流守恒公式相加，可得时间T内的流守恒公式为

式(3)为在整个时段T内，从每个时段的传输链路流入Sj的流值的和与每个时段流出Sj的流值的和相等。此外，对于源节点A 和目的节点D，在时间范围T内，有

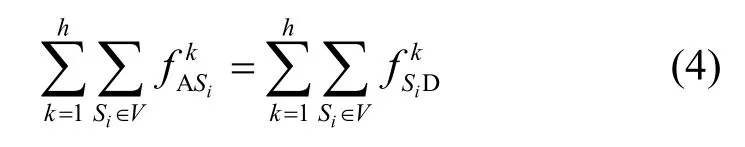
即从源节点A 流出的数据流应与流进目的节点D的流值相等。

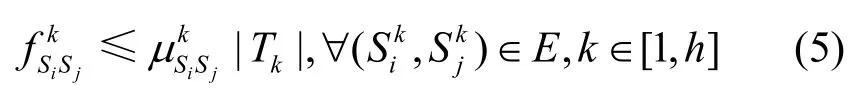
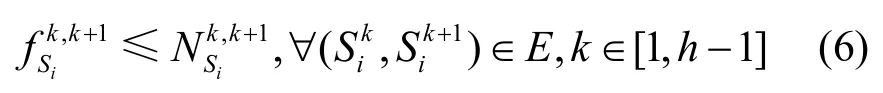
3) 业务时延约束

对于任意任务Mi∈M，其属性为假设该任务所规划路径上的所有链路的所处时段的集合为Δi，且时段集合Δi中的最早时段为minΔi，最后一个时段为maxΔi。则为该业务规划的路径上的流值和应该满足

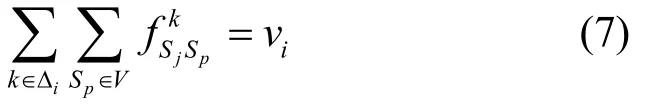
此外，规划路径的时间段应在其时延需求范围内。具体地，为任务Mi规划路径所有链路所处的最早时间不早于任务的释放（开始）时间，路径中所有链路的最晚时间不能大于任务的截止时间，即

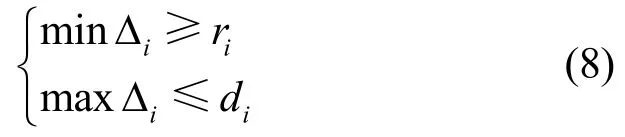
由于问题式(1)的优化目标为非线性约束，而其他约束条件均为线性约束，因此该最大概率保障业务时延的路由问题为非线性规划问题。

3 系统模型

本节为解决该非线性规划问题，提出了随机时变图模型支持将该问题映射为路由问题。首先，对时变的网络拓扑进行了建模。然后，考虑了链路资源的随机特性，利用一阶矩和二阶矩对链路资源的随机性进行了建模，构建了随机时变图模型。最后，通过示例对映射后的路由问题进行了描述。

3.1 拓扑表征图模型

考虑一个网络包含卫星集合S和地面站集合G，其中，卫星集合S={S1,…,SN]包含N颗卫星，地面站集合G={G1,…,GP]包含P个地面站，待传输任务集合M={M1,…,MQ}包含Q个任务，可以用快照刻画出h个时段的节点间连通关系。另外，一个时段的任务可借助该节点内的存储在下一时段进行传输，从而联合利用多时段的存储资源。对于任一卫星Si∈S，若其属于第k个快照，将其定义为。因此，可以将相邻2 个快照中同一卫星的2 个节点用有向链路相连，且方向指向时间增大的方向。网络拓扑可以用有向图G=(V,E)来表示，其中点集合V包含了所有时段的卫星节点，边集合E包含了所有快照内的传输链路以及快照间的存储链路。

为了更清楚地阐述拓扑的图模型表征过程，构建一个简化的4 无人机网络，如图2 所示。首先将无人机网络的时间段T分成3 个小时段,使每个时段内网络拓扑不变。无人机网络在3 个小时段内有不同的拓扑，分别采用节点和链路刻画每个快照的拓扑。自然地，同一无人机在相邻2 个快照内有2 个节点，用有向链路相连。给定无人机S3，可将其第一个快照的节点与第二个快照内的节点相连，从而获得其存储链路。这种表征方式支持存储携带转发模式，比如将在第二个时段将数据传输给，通过将数据缓存给，最终可在第三个时段将数据传给

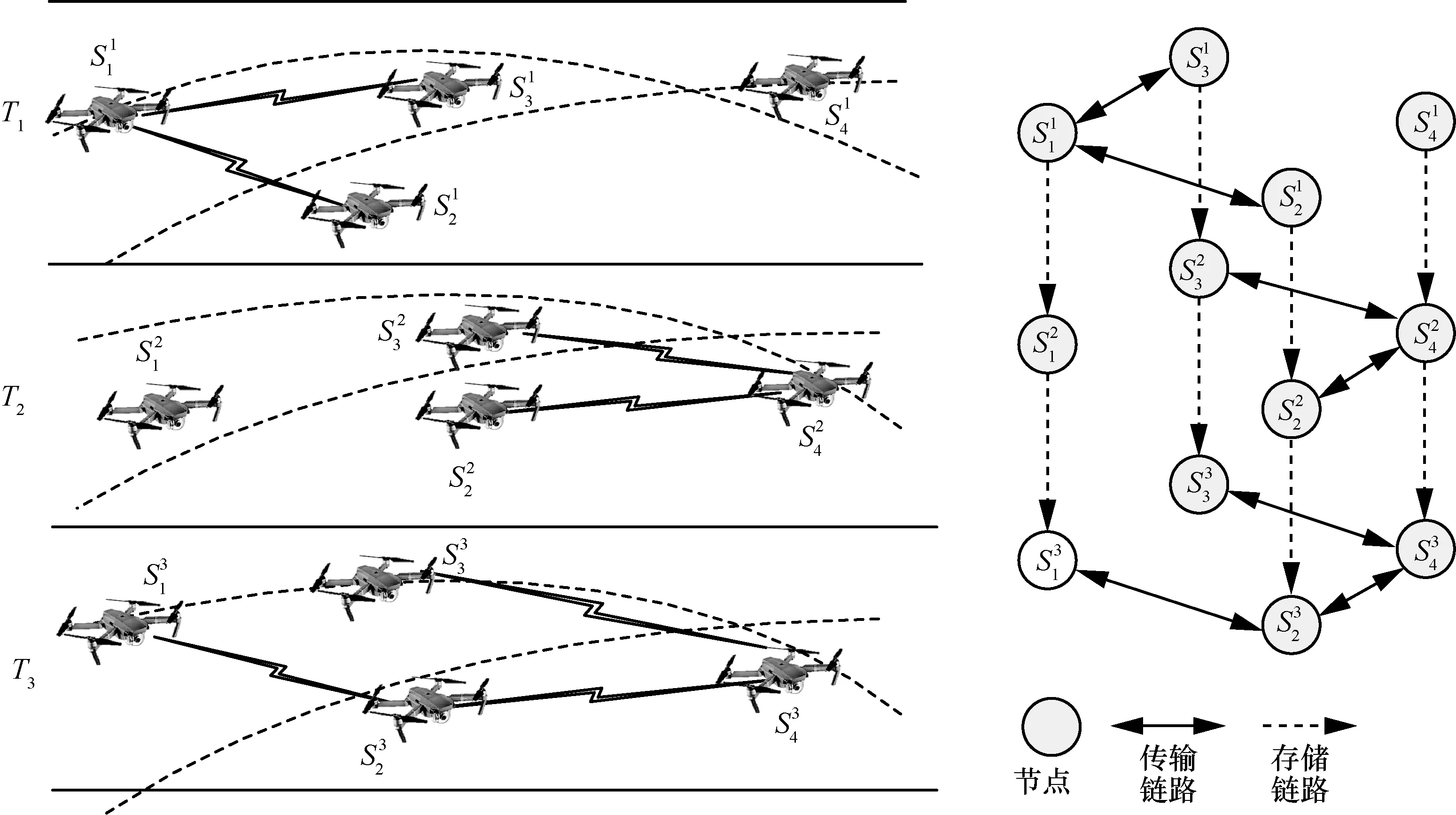
图2 网络拓扑图模型表征

3.2 链路资源的随机性表征

对于网络拓扑G=(V,E)，边集合E中的传输链路具有传输速率、传播时延等属性。而存储链路属性为节点的可用存储空间。事实上，由于业务的随机占用，链路可用传输时间服从一定概率分布，可根据链路速率的历史统计信息，获取一阶原点矩来刻画在一个时间段内链路可用时间的均值，计算二阶中心矩来刻画可用时间的方差。基于此，假设链路速率分布服从高斯分布，可知链路在不同时段内可用时间的概率分布。具体地，对于任意链路表示链路在时段Tk内可用时间随机变量，表示链路在时段Tk内可用时间一阶原点矩-均值，表示链路时段Tk内可用时间二阶中心距-方差。对于任意节点表示其能从第k个快照向第k+1 个快照缓存的容量均值，由于存储容量为定值，所以其方差为0。因此，对于图2 所示网络，可获取其随机时变图模型如图3所示。

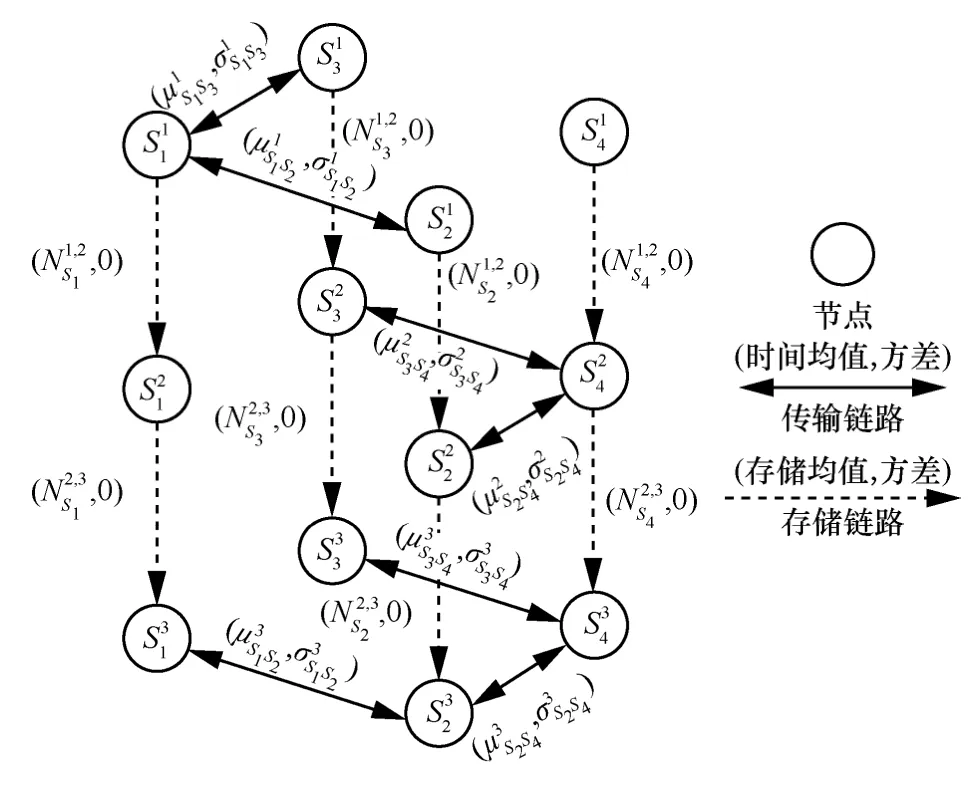
图3 随机时变图模型

3.3 问题映射

事实上，对于任务∀Mi∈M，由于其任务释放时间和截止时间已给定，可通过加入任务需求链路来表征任务的时延需求。例如，任务M1的释放时段是第一个小时段，截止时间是第二个小时段，且其源节点为S1，目的节点为S4。则可以在第一个小时段插入一个辅助源节点与相连，作为任务M1的释放链路。相似地，可以在第二个小时段插入一个辅助目的节点与相连，作为任务结束链路。业务的时延需求表征如图4 所示。因此，任务M1的时延保障路径查找问题可转化为查找源节点到目的节点的路径。

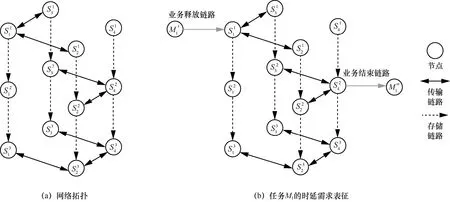
图4 业务的时延需求表征

基于图 5 针对业务M1的概率图模型G=(V,E)，假设M1需在前h个时段内完成。问题式(8)的决策变量可由决定每条链路的流量大小转变为是否选择该链路传输。定义链路决策变量xe为是否选择链路e∈E的0/1 变量。xe=1 表示选择链路e来进行传输，xe=0 表示不选择链路e。特别地，对于任意传输链路和存储链路其链路决策变量分别为和。链路e满足任务需求的概率为Pe，则问题式(1)可转化为

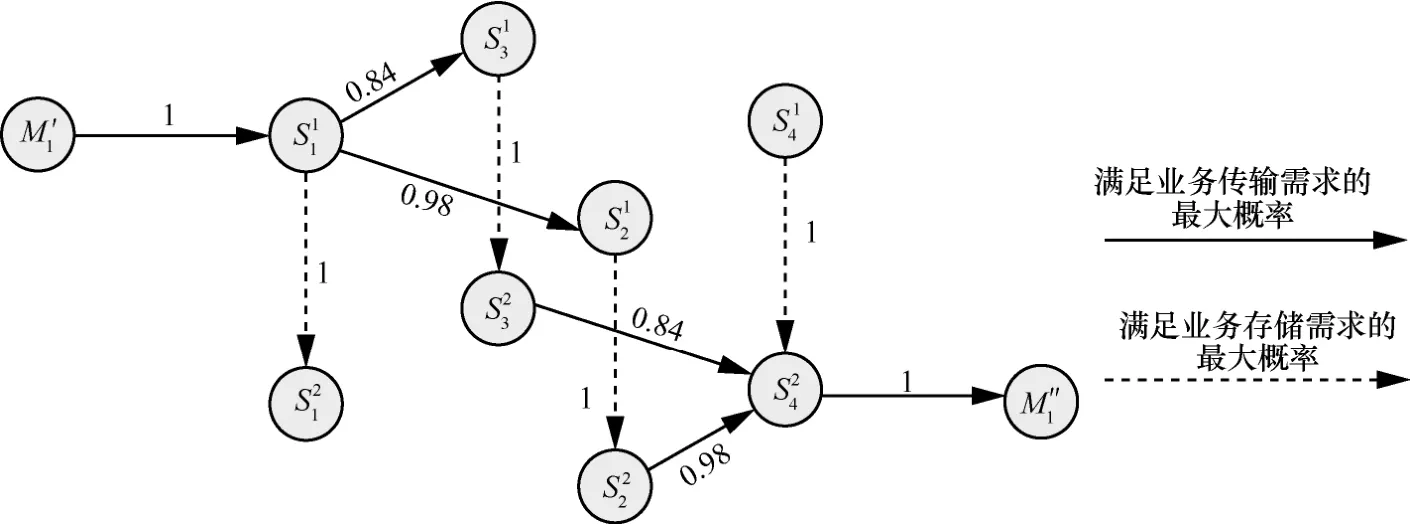
图5 业务M1的概率图模型

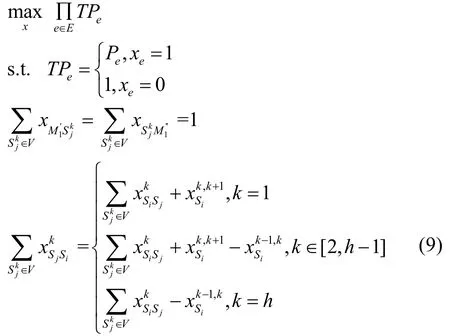
其中，xe∈{0,1}。

此时，业务最大概率时延保障路由问题可被转化为式(9)，该问题为从所有源节点到目的节点满足传输需求的路径中找出最大概率满足需求的路径。所以对于不选择传输的链路，其链路概率对最终结果没有影响，将其概率设为1。此外，因为只需找一条路径，所以从源节点出发的链路中只能选择一条链路，同理，所有指向目的节点的链路中也只能选择一条。

3.4 问题描述

为清楚地解释问题式(9)，选取图3 中的前2 个时段，构建了如图6 所示的简单网络的图模型。时间范围T被拆分成了2 个时段且每个小时段长2 min。所有链路速率均为60。链路上标注的数字为链路可用时间的均值和方差。由于网络业务的随机占用，例如图6 中链路标注(100,400)表示链路可用时间均值为100 s，方差为400 s2。若节点S1需要向S4传输4 800 单位数据，任务在第一时段产生，且需要在最多4 min 内完成。则当路径与路径中每条传输链路具有最小80 s 的可用传输时间时，可满足任务的传输需求。但是每条传输链路可用时间均为随机变量，且为高斯分布。根据链路速率均值和方差，链路能保障任务的传输需求（即提供最小80 s 可用传输时间）的最大概率分别为0.84、0.84、0.98、0.98。存储链路方差为0，概率为1。则路径与路径能满足业务传输需求的最大概率分别为0.84×1×0.84≈0.71 和0.98×1× 0.98≈0.96。显然，虽然具有更高的确定性传输的数学期望，由于其方差较大，不能以大概率满足业务传输需求。

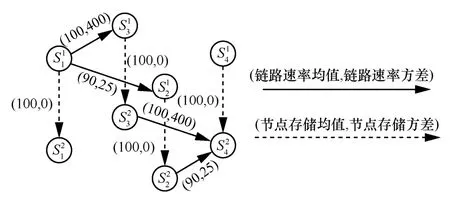
图6 简单网络的图模型

4 最大概率保障业务时延路由算法

本节首先给出了最大概率业务时延保障路由算法，然后使用样例解释了算法的运行步骤，最后证明了算法的最优性并分析了算法的复杂度。

4.1 路由算法

为求解问题式(9)，给出了基于图论的最大概率业务时延保障路由算法，如算法1 所示。

算法1最大概率业务时延保障路由算法

输入任务Mi概率图模型G=(V,E)，存储链路与任务释放链路和结束链路权重标注为概率1，其他任务链路的权重为，源节点目的节点

输出源节点到目的节点概率最大（权重积）最大的路径

步骤1每个节点u∈V设置2 个参数，一个参数概率变量P(u) 表示从源节点到该节点的路径中能够满足业务Mi时延需求的最大概率，另一个参数F(u) 表示节点u∈V的最大概率路径的前一跳节点。初始时，=1，且P(u)=0,u∈V,u≠此外，源节点前一跳节点为其本身，其他节点前一跳节点为空。

步骤2设置 2 个点集集合S和S′，且S∪S′=V。初始时S=∅，S′=V。

步骤3当S≠V时，寻找S′中P值最大的节点u=argmax{P(u)|u∈S′}。将节点u从S′中删除并将其加入集合S。对于集合S′中节点u的每个邻居节点v，若有P(v)＜P(u)Pu,v，则P(v)=P(u)Pu,v且F(v)=u。重复该步骤直到S=V。其中，Pu,v表示链路速率大于满足业务传输需求的最小速率的概率。

算法1 的核心思想是采用贪心策略，利用集合S′记录当前节点，采用集合S记录所有当前节点中源节点能够在最大概率保障时延的情况下到达的节点。初始时S′节点集合为集合V。不断从S′中找出概率值最大的节点，将该节点的邻居节点进行概率更新操作，并将该节点从S′中取出加入S中。这种层层更新的策略能够保障最终得到的路径为最大概率路径。

所提路由算法由SR 协议实现，该协议只有路由源节点需要获取网络的全局信息进行路由计算，其他节点只需知晓网络的基本连通关系即可。由于卫星沿固定轨迹运动，每颗卫星知晓所有网络中卫星的轨迹参数，因此每颗卫星可计算出任意时刻任意2 颗卫星间可否进行通信（即2 颗卫星间的链路是否连通）。此外，对于网络状态信息，地面测控中心可实时监控网络链路状态信息，可根据历史链路信息与路由策略，预测出未来时段的链路状态信息，并可通过地面测控网络将该信息上注给SR 协议中有限个路由源节点。

根据网络中链路权重类型的不同，路径可分为不同类型。当链路权重为时延、费用、代价等时，所求路径为加性权重最小路径，即所求路径满足在所有源到目的节点的路径中链路权重和最小，Dijkstra 算法可直接求解该类路径；当链路权重为本文中的成功概率、误码率等时，所求路径为乘性最大路径，即所有路径中链路权重积最大的路径。Dijkstra 算法无法直接求解该类路径，可通过将每条链路的权重转化为，再利用Dijkstra 算法求解。当链路权重为带宽（即链路速率）时，所求路径为凹性最大路径，即所有路径中链路最小权重值最大的路径。Dijkstra 算法无法直接求解乘性与凹性最大路径。

本文所提算法可直接求解乘性最大路径，不需要进行权重转换与计算，可节省路由协议的计算和存储开销。此外，对于凹性最大路径的求解，仅需将所提算法步骤 3 中的判断操作变为若P(v) ＜min{P(u),Pu,v]，则有P(v)=min{P(u),Pu,v]，即可实现凹性最大路径的求解，其中P(u) 为源节点到节点u所有路径中的最大凹性权重值（如最大带宽），Pu,v为链路(u,v)的权重值，且该凹性路径求解具有最优性。所提变形Dijkstra 算法弥补了原始Dijkstra 算法计算乘性和凹性路径的空白。

4.2 样例说明

为了清晰地阐述算法的运行过程，图7 给出了算法的运行样例。首先，图7(a)刻画了简单的网络拓扑，业务M1需要从节点S1传输到节点S4，该传输任务需要在2 个时段内完成。为保证算法求出的路径满足业务时延需求。在第一个时段插入了业务释放链路，并在第二个时段插入了业务结束链路。算法的目标为寻找到的路径中最大概率保障业务时延的路径。

图7 算法运行样例

4.3 最优性证明和复杂度分析

引理1算法1 运行时，S′中每个节点加入S时都已找到最大概率路径，且该最大概率值为节点概率值。该路径可由每个节点的上一跳节点属性获取。

证明采用归纳法证明。

第一次从S′向S中加入节点时所加节点为源节点本身，引理成立。

假设前k次从S′向S中加入节点时引理均成立，则在第k+1 次从S′向S中加入节点时引理仍成立。定义第k+1 次从S′加入S中的节点为u，则节点u为集合S′中概率值最大的节点。用反证法证明。假设存在一条从源节点到节点u的概率值更大的路径l，该路径的概率值Pl大于节点u的概率值P(u)。路径l包含除节点u外至少一个在S′中的节点。定义该节点为节点x，且节点x的上一跳节点为y。节点u的路径情况如图8 所示，由源节点经由F(u)到达节点u的路径为算法所找路径。由源节点经由节点y和节点x到达节点u的路径为假设存在的概率更高路径，即路径l。根据算法1 可知，在第k+1 次从集合S′中之所以选择节点u，是因为集合S′的所有节点中u概率值最大。所以有P(u)≥P(x)。由于x到u的路径概率，因此路径l概率为，与假设矛盾，故引理得证。

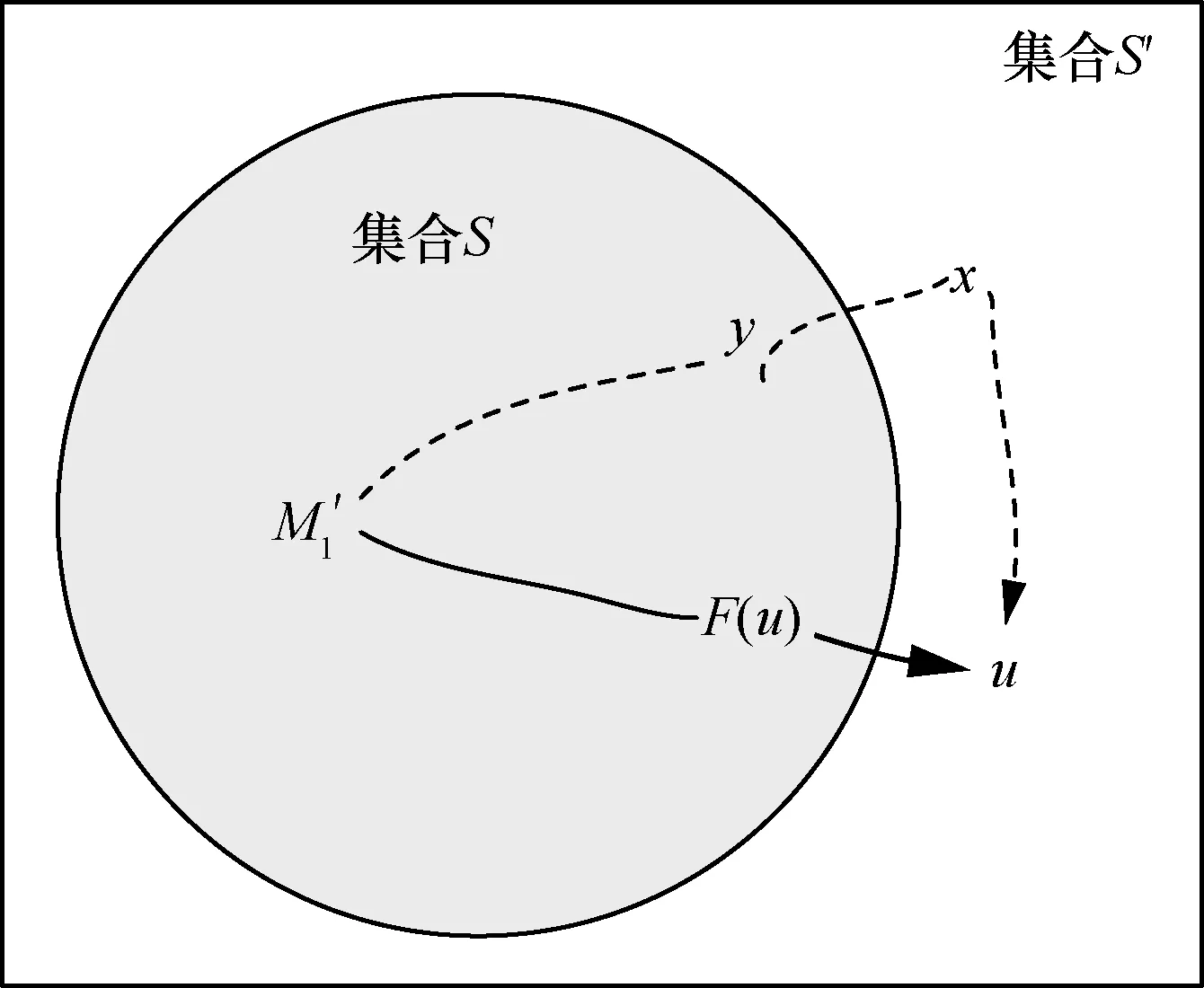
图8 节点u 的路径情况

引理2对于n个节点、m条边的随机图模型，算法1 的时间复杂度在网络稀疏时为O(n2)，在网络稠密时为O(m)。

证明算法1 执行过程主要分为2 个步骤：1)集合V中的n个节点都要从集合S'中被挑选出来；2) 每个节点被挑选完后要判断是否对节点的邻居节点概率值进行更新。针对步骤1)，每次挑选都要从S'中选出概率值最大的节点，时间复杂度为O(n)。选择了n次，复杂度为O(n2)。对于步骤2)，每个节点都会判断其邻居节点是否需要概率值更新，即图中所有的边都被执行了判断操作，所以总共执行了O(m)次；因此算法复杂度为O(n2+m)。易知，在网络稀疏时，有n2＞＞m，所以复杂度为O(n2)；在网络稠密时，m=n(n-1)/2，此时算法复杂度为O(m)。证毕。

5 结束语

本文针对现有路由算法未考虑链路传输时间的随机特征，提出了时变场景中表征链路随机特性随机时变图模型。基于该图模型，将最大概率保障业务时延的路径选择问题建模成非线性规划问题，并且提出了最优的多项式时间图论解法。在未来工作中，将增加多业务随机特性的表征，考虑如何最大概率地保障多业务的时间确定性路由问题。