基于DKF的IMU误差预测算法

秦闪闪，陈夏兰，徐 颖，马满帅，王 莹，梁任腾，杨子佳

(1.中国科学院空天信息创新研究院导航系统部，北京 100094；2.中国科学院大学电子电气与通讯工程学院，北京 100049；3.北京信息科技大学信息与通信工程学院，北京 100192)

0 引言

全球导航卫星系统(Global Navigation Satellite System，GNSS)/惯性导航系统(Inertial Navigation System，INS)组合导航的核心是如何有效地将GNSS观测量与惯性测量单元(Inertial Measurement Unit，IMU)测量结果结合得到载体导航结果的最优估计，在目前的组合导航技术中，包括松耦合、紧耦合和超紧耦合[1]。其中松耦合在软件层面组合，将GNSS接收机导航定位结果和INS测量结果进行滤波融合[2-3]，当前常用的融合算法是卡尔曼滤波(Kalman Filter，KF)[4-5]。KF利用GNSS观测量和IMU测量结果解算得到IMU误差的估计值，再将估计值反馈给IMU，IMU测量结果经过估计值校正后作为导航解输出。GNSS/INS组合导航系统长时间运行的精度更多地依赖于GNSS，然而实际中存在各种随机的或复杂的误差源，如可见卫星数目、多径效应和仪器内部的量测噪声等，都会使得卫星导航系统的量测噪声随时发生变化，标准KF难以对上述变化进行检测和调整，导致其使用的噪声统计特征与事实发生偏差，无法得到最优滤波结果，甚至会出现滤波发散现象[6]。为了克服标准KF在组合导航中应用的缺点，研究者们开始针对其设计与应用场景相适应的滤波算法。

针对全球定位系统(Global Positioning System，GPS)测量值发生较大变化时如何提高KF的滤波精度和鲁棒性的问题，卞鸿巍利用对实际新息的测量计算直接修正卡尔曼滤波器增益，但需要采用GPS测量系统为INS提供外部修正信息[7]。付梦印研究了应用于惯性技术领域的相关法自适应滤波和Sage-Husa 自适应KF，然而带有衰减因子或记忆因子的卡尔曼滤波器系统状态维度增加，计算量加大[8]。高为广和杨元喜使用反向传播(Back Propagation, BP)神经网络在线修正自适应滤波器的预测值，该算法提高了滤波精度和可靠性，但算法中提到的“经过复杂函数映射到当前函数的网络预测值”难以获取[9]。M.Narasimhappa等优化了Sage-Husa自适应鲁棒KF算法，更新了自适应比例因子的计算方法，从而有效降低了估计误差的平均值和标准差，但增大了系统计算的复杂度[10]。S.Hosseinyalamdary提出了一种使用递归神经网络训练组合导航观测模型的方法，从而克服了因INS误差模型的复杂性导致的计算误差，但大大增加了算法的计算量[11]。

很多高动态导航载体，如快速运动的无人机，也使用GNSS/INS组合系统来导航。由于GNSS在高动态下跟踪环路可能失锁，在信号被掩盖及多径效应等场景下测量值不准确甚至没有，导致此时的载体只能依赖IMU进行导航，导航结果会在时间积累下迅速失去有效性。本文拟解决的问题就是在GNSS接收机输出中断或测量结果不可信时，如何在IMU独立导航条件下尽可能保持较高的导航精度。关于这个问题，也有学者进行研究，如德国卡尔斯鲁厄大学的研究者通过在无人机上添加磁强计和高程计以解决组合导航的这个问题[12]；荷兰特温特大学的研究者则将深度学习的思想引入KF，利用循环神经网络和长短期神经网络开展了初步的研究[11]。

1 KF算法

KF估计的未知量为状态向量，表示为x∈Rn，其是一个时间变量，即xt表示时刻t的状态向量。其与过去直到现在的观测矢量z1∶t相关，z∈Rm。设初始状态为x0，则xt的概率为Pr(xt|z1∶t,x0)。根据极大似然估计(Maximum Likelihood Estimation，MLE)

(1)

系统当前的状态与过去的状态有关，即

(2)

去掉常数

(3)

应用前一个状态向量的边缘化得到基于前一个状态向量的状态向量估计，即

Pr(x1∶t-1|z1∶t-1,x0)dx1∶t-1

(4)

基于马尔可夫假设，即

Pr(xt-1|z1∶t-1,x0)dxt-1

(5)

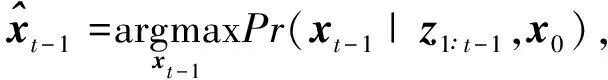
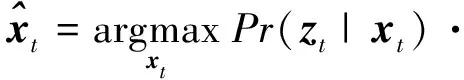
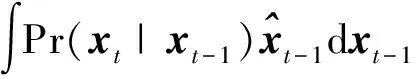
(6)

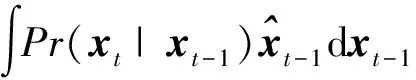
在KF中，系统状态与上一时刻的状态和系统模型有关，即

xt=f(xt-1)+εt

(7)

式中，εt为系统噪声模型。同时系统状态通过观测方程g映射到观测量zt∈Rm，即

zt=g(xt)+ωt

(8)

式中，ωt为观测噪声模型。在KF中，状态模型和观测模型都是线性的，分别用F和G矩阵表示。系统模型为

xt=Fxt-1+εt

(9)

同理，观测模型为

zt=Gxt+ωt

(10)

假设KF中系统噪声和观测噪声都服从正态分布

εt～N(0,Qt)

(11)

ωt～N(0,Rt)

(12)

式(11)和式(12)中，Qt和Rt分别为系统噪声和观测噪声的协方差矩阵。

KF过程分为预测过程和更新过程。系统当前状态由前一时刻状态预测，即

(13)

状态向量的上标“-”表示预测量，上标“+”表示更新量。采用误差传播法，根据前一时刻状态向量的协方差矩阵估计当前状态向量的协方差矩阵

(14)

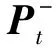
在更新过程中，当前状态的更新值由当前观测值和预测值得出

(15)

则状态变量更新值的协方差矩阵为

(16)

式中，Kt为卡尔曼增益

(17)

2 深度卡尔曼滤波(DKF)

为了解决KF更新过程中观测量获取不到的问题，在KF中添加建模步骤，即在KF中加入隐变量。隐变量在状态向量中不可见，但能决定状态向量，用ht表示，是时间相关变量。当前系统状态取决于过去T个时刻隐变量的值ht-1∶t-T。

假设当前系统状态只与当前隐变量有关，即不直接依赖于过去系统状态xt-1∶t-T，马尔可夫假设不成立。新的假设不仅符合很多系统，而且简化了计算。

设当前隐变量与过去隐变量和系统状态之间的映射关系为φ，即

(18)

当前系统状态直接与当前隐变量相关

(19)

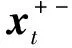
(20)

(21)

式中，Wh=[Wxh,Whh]。建模任务转化为估计Wh和Wxx。如图1所示，深度卡尔曼滤波(Deep Kalman Filter，DKF)的上层网络与传统KF基本一致，建模步骤位于下层网络。根据IMU随时间积累的特性，在时间维度上使用深度学习算法进行建模。

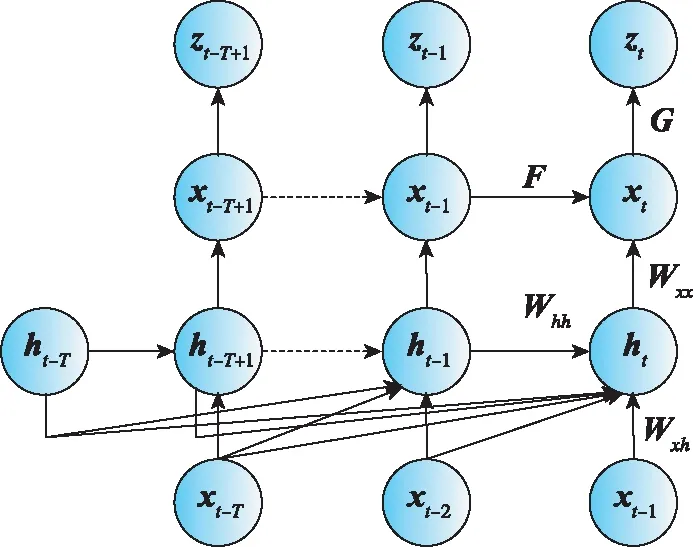
图1 DKF的概率图模型

2.1 模型参数估计

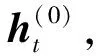
(22)

基于式(22)的结果估计隐变量

(23)

根据式(21)，计算系统状态可以转化为计算Wxx，同理，计算隐变量转化为计算Wh。将式(20)和式(21)代入式(22)，则

(24)

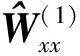
(25)

隐变量和状态向量的迭代估计一直持续到算法收敛到其解，最后确定系统模型并得出状态向量的估计。P.Mirowski和Y.Lecun的研究表明,EM算法可以使用递归神经网络训练[13]。

EM算法最终收敛到凸函数的全局最大值，然而对于一些建模为非凸函数的系统，EM很有可能收敛到局部极大值，所以如何找到式(24)和式(25)中的最大值是一个挑战。

DKF的建模过程分为两步：通过过去的系统状态和隐变量估计当前隐变量；通过当前隐变量估计当前系统状态。

用隐变量估计重新构造式(6)，则

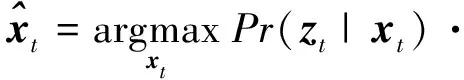
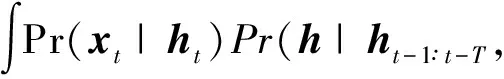
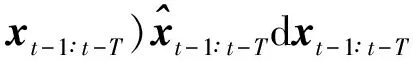
(26)

(27)

将式(21)代入式(26)，得到

(28)

则Wxx的梯度为

(29)

Wh的梯度为

(30)

利用梯度下降方法最小化能量函数。建模系统的参数矩阵Wh和Wxx为

(31)

(32)

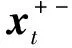
顺应时势的转型要求电视新闻记者在努力学习最新科学技术、传媒技术的同时，更新理念，深化对不同业务的理解，成为一个“新闻全才”。更重要的是，媒体融合时代对主流媒体新闻记者职业操守的要求更加严格，电视新闻记者务须确保采编的所有新闻内容真实、客观，并且能够引导正确社会价值观。在遵循媒体融合时期新闻传播规律的基础上，电视媒体可尝试打造具有“标签”效应的品牌记者，如知名调查报道记者、知名环保栏目记者、知名时政新闻记者等。

2.2 长短期记忆网络(LSTM)

递归神经网络的缺陷是梯度爆炸和梯度消失[14]。当T比较大且建模时间较长时，梯度会在几层网络中做乘法运算，则较大的梯度乘积更大，最终导致梯度爆炸。反之，如果梯度较小，乘积则趋近于零，从而导致梯度消失。为了抑制递归神经网络中的这种效应，长短期记忆网络(Long Short-Term Memory，LSTM)中采用了门记忆[15]，计算单元具体结构如图 2所示。

图2 LSTM(Peephple connection)结构图

LSTM在递归神经网络中加入了判断信息是否有用的处理器——cell，一个cell当中放置了三扇门，分别叫作输入门、遗忘门和输出门。用it表示输入门，ot表示输出门，ft表示遗忘门，这三种门都可以用线性函数和非线性函数的组合来表示

(33)

式中，σ表示非线性函数，线性函数由参数矩阵表示。cell的状态ct和隐藏层ht按如下计算

ct=ft°ct-1+it°tanh(Wxxt+Whht-1)

(34)

(35)

式中，°表示按位相乘。对于具有长期相关性的输入数据，输入门可以保持以前状态向量的信息，并且可以访问以前状态向量的梯度。因此，梯度在反向传播过程中不会爆炸或消失。遗忘门控制了模型的复杂性，并删除了不相关的过去状态向量。

基于DKF的导航系统分为训练部分和应用部分。已经知道的是：如果GNSS测量值能够得到，将其作为观测值输入到KF中，应用系统模型和观测模型来预测和更新系统状态，同时使用DKF对IMU模型进行训练，如图3(a)所示；如果GNSS失锁或其他无法获得GNSS数据的情况发生时，KF只能完成预测过程，此时应用训练好的模型进行导航解算，如图3(b)所示。

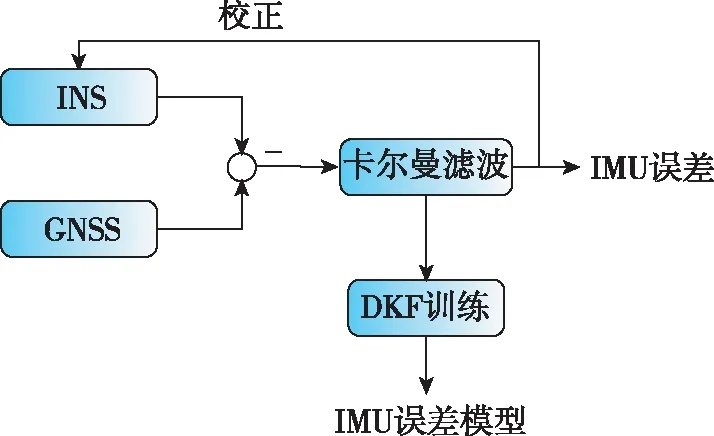
(a)DKF训练模型

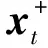
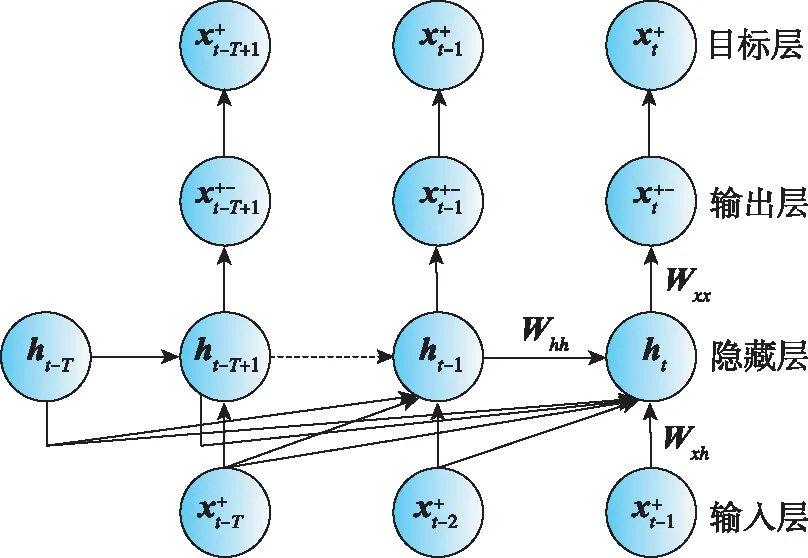
(a)DKF训练网络结构图

3 基于DKF的仿真分析

以仿真数据为例对算法进行有效性验证，仿真数据长400s，采样频率1Hz，包含有两种数据：第一部分是设定的真实导航数据；第二部分是仿真输出的IMU数据。每一秒都包含有变加速运动导航载体的实时真实速度和IMU速度信息。

在GNSS失锁时，作为自主式导航系统，导航载体上的INS仍然正常运行，其初始导航状态是GNSS失锁前最后时刻输出的导航状态。实验所使用的数据是长400s的含有标识的IMU数据以及在真实导航数据上仿真的GNSS数据。在GNSS失锁时，INS单独运行，其误差迅速增大，失锁200s后，东北天坐标系下3个方向的速度误差已经分别达到1.1537m/s、1.2146m/s和0.3332m/s。

为了评估算法的结果，将400s的数据划分为两段：前200s数据作为训练集，用来测试和评估；后200s数据作为测试集，用来验证模型的有效性。前200s训练部分，在真实导航数据上添加噪声作为GNSS数据，将其与IMU数据组合通过KF得到IMU误差，该IMU误差作为DKF的训练数据使用。后200s使用训练得到的IMU误差模型预测IMU误差，用其校正IMU数据，并和设定的真实导航数据进行比较，以评估DKF的有效性。

DKF网络设置输入序列长度为5，中间节点数为50，迭代55次，DKF模型预测的IMU误差结果如图5(a)和(b)所示。

如图5(a)所示，在GNSS失锁后，使用DKF算法训练的模型估计出IMU的误差与实际IMU误差接近，将其作为校正量代入IMU数据中，能够保持一定时间的高精度导航。如图5(b)所示，如果在GNSS失锁后使用DKF进行IMU误差校正，200s后速度误差只增长到0.3746m/s，且200s内的平均误差只有0.1350m/s。与GNSS失锁200s后的系统误差1.1537m/s相比，DKF对短期内导航解的改善是显而易见的。

DKF通过前5个时刻预测下一个时刻的IMU误差，平均估计使用前5个时刻的平均值作为下一个时刻的IMU误差，两者的对比实验结果如图5(c)和(d)所示。如果在GNSS失锁后使用平均估计进行IMU误差校正，由于平均估计预测的IMU误差维持在GNSS失锁时刻的数据，在200s内误差达到1.1203m/s，200s内平均误差为0.5890m/s。平均误差对于GNSS/INS组合系统的持续导航改善不如DKF。

GNSS失锁后，GNSS/INS组合系统由于丢失观测量而无法使用KF，但是基于持续输出的IMU数据，可以使用卡尔曼的预测部分对IMU误差进行估计，卡尔曼预测和DKF的对比实验结果如图5(e)和(f)所示。如果在GNSS失锁后使用卡尔曼预测进行IMU误差校正，其估计的IMU误差在200s内达到0.7479m/s，200s内平均估计误差为0.4421m/s。卡尔曼预测对于GNSS/INS组合系统的持续导航改善不如DKF。

最小二乘估计作为常用的估计方法，在曲线拟合方面效果显著，可以使用最小二乘估计拟合GNSS未失锁前的IMU误差模型，从而预测GNSS失锁后的IMU误差。最小二乘估计和DKF的对比实验结果如图5(g)和(h)所示。如果在GNSS失锁后使用最小二乘估计进行IMU误差校正，其估计的IMU误差在200s内的估计误差达到0.9725m/s，200s内平均估计误差为0.3352m/s。最小二乘估计对于GNSS/INS组合系统的持续导航改善不如DKF。

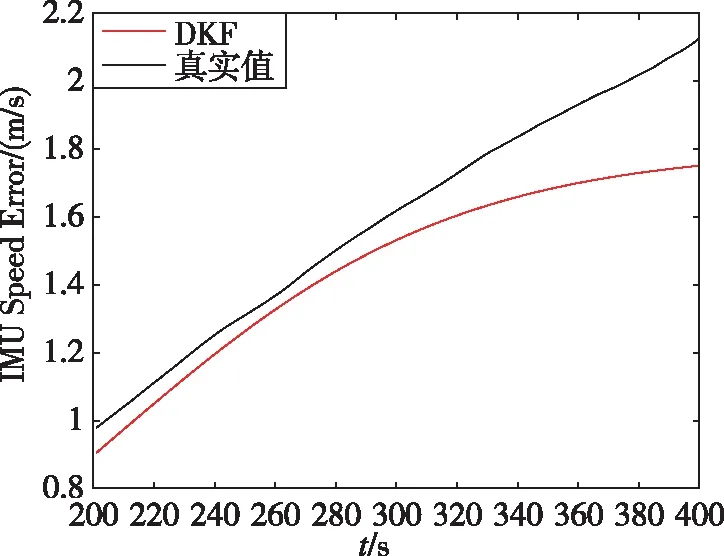
(a)DKF预测结果图

为了进一步说明DKF算法的有效性和性能，将DKF的估计误差与平均估计、卡尔曼预测和最小二乘估计进行对比，结果如图6所示。

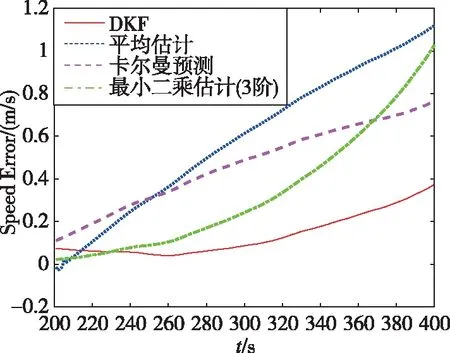
图6 四种方法的估计误差对比图

如图6所示，在GNSS失锁200s内，对于GNSS/INS组合系统的持续导航改善最好的是DKF，其次是最小二乘估计。

4 结论

针对GNSS/INS组合系统中GNSS失锁后导航精度的维持问题，本文提出了一种基于LSTM的DKF算法。首先使用GNSS数据和IMU数据通过KF获取失锁前的高精度导航数据；其次，基于高精度导航数据训练IMU误差模型；最后，在GNSS失锁后使用IMU误差模型进行误差校正。算法分析与实验结果表明：

1)DKF算法在时间维度上分为2个阶段执行，实现了基于历史信息对当前IMU误差的校正。因此具有比传统KF更高的信息利用率，可以在GNSS失锁时维持GNSS/INS组合系统的高精度运行。

2)本文提出的DKF算法依靠LSTM对序列信息的敏感度对IMU误差进行建模，而机器学习的本质要求含有大量信息的大数据集进行实验。在实际的复杂环境中如何获取这些数据并且保证算法的实时性，值得做进一步研究。