基于遗传算法的寻优解卫星星座优化设计策略

水浩然，陈 勇，陈宏新

(1.北京京航计算通讯研究所，北京 100074；2.海装重大专项装备项目管理中心，北京 100083)

0 引言

卫星星座优化设计本质上是卫星部署合理性问题。在优化设计前，需要对选定的卫星星座构型的轨道模型进行分析。针对轨道参数策略上的设定，以偏心率与近地点幅角不变为前提，修改轨道倾角和轨道半长轴，再使用改变的参数推算出卫星轨道的升交点赤经与真近点角。以这些参数去部署卫星星座，相较于最原始的部署办法，可以实现增大卫星星座观测目标区域和缩短重访周期的效果。但这些办法仅仅是卫星星座优化设计的第一步，采用不同的轨道模型也可以实现不同的星座观测效果。

周砚茜和T.Liu等提到，卫星星座的发展具有数量集群越来越多、网络效果特性繁多、网络品种繁茂等情况[1-2]。蒋炫佑和A.Tosyali 等陈述了符合高斯算法的M-APSK信号卫星组网搭建规则，并利用这种卫星组网搭建规则实现了新型星座构型的搭建，大幅降低了星座的设计难度，也有效提高了卫星星座性能[3-4]。田野和M.Bonnet 等关于当前全球低轨卫星发展的现状做了较多专业研究，针对有关部分低轨卫星星座组网策略，组合星座能够同时完成全球覆盖，并能实现DOP值与可见星数量在全球区域内的均匀分布[5-6]。E.A.Mikrin、T.Shtark、H.Xu和关梅倩等引出了导航卫星系统设计的低轨化办法[7-10]。刘海蛟等提出了低轨卫星拥有轻盈、延时间隔短和成本较低等特点，通过星座融合可实现全球范围内的无空白区域覆盖[11]。蒋季给出了针对全球范围内的覆盖星座设计方案[12]。刘洋等通过激光链路的手段为星座体系输入动力，使星座体系能够实现对中国领土面积的无缝观测效果[13]，极大提升了星座对中国区域的监测效率。

而利用遗传算法的优化策略，对卫星星座个体编码、构造适应度函数及演化等手段也可以实现较好的优化结果。马原野[14]与沈欣等[15]提出了使用优化算法进行快速优化的设计策略。陈宏君选用遗传算法寻找搭建数学模型的最优解，调节遇到各个问题之间的问题，提升了卫星星座的整体效能，极大节约了经济资源与时间资源[16]。刘蕊蕊等使用遗传算法对BP神经网络进行算法优化，提高了面相优化问题的收敛性，同时验证了算法的有效性[17]。谷加臣等利用基于遗传算法的神经网络研究方法为本领域内的研究提供了多种借鉴[18]。侯远韶基于蚁群优化办法对决定的路径实行维度升迁的划分，以达到目的功效性能的提高[19]。胡粔珲结合遗传算法与蚁群算法，搭配使用两种算法的优化特性，巧妙地规避掉算法约束[20]。熊起利用遗传与蚁群结合方法建模，妥善总结出支持其研究的办法[21]。

本文主要基于遗传算法，在选定的卫星星座构型中，寻找卫星星座较优解。本文区别于其他研究学者在面向星座优化设计问题中使用的加权赋值和主观优化等办法，通过使用遗传算法并结合个体编码、适应度函数等手段，打破选定方案中的一部分固有约束，将星座内的卫星个体逐个编码，通过科学的计算，实现对星座内最优解的寻找，并使用寻找到的最优解构建Walker星座组网，进而得到更加高效的星座构型优化模型。

1 卫星星座构型优化设计理论

星座的优化设计必然无法脱离对轨道理论的选用和对星座构型的选取。在引入使用的优化设计策略前，需要先行探讨选用的卫星星座构型，涉及使用到的卫星星座设计理论。

1.1 “深圳一号”卫星星座构型

选取“深圳一号”卫星星座构型作为优化算法使用并执行的基础构型[22]。图1所示为“深圳一号”卫星星座组网的几何设计图。

图1 “深圳一号”卫星星座组网几何设计图

“深圳一号”卫星星座构型对应的有关参数见表1，含有所用到的星座属性与指标。

表1 卫星星座构型轨道属性与指标

1.2 卫星坐标系

卫星星座优化计算量庞大，为了便捷使用计算法则、利用计算程序，选取代表卫星惯性运动的坐标系，分别定义为卫星轨道坐标系和地心赤道惯性(Earth-Centered Inertial，ECI)坐标系，图2所示为两坐标系的几何示意图。

图2 两坐标系几何示意图

1.3 卫星轨道参数

卫星星座的优化设计，需要首先对涉及的卫星星座设计优化模型进行研究，引入轨道六根数：轨道半长轴a、轨道倾角i、偏心率e、升交点赤经Ω、近地点幅角ω和平近点角M，这里提到的6个轨道参数称为经典轨道六根数[23]。本文选用通常默认研究的右手惯性坐标系，若有时刻t下对应的卫星参数f、r，则用式(1)表示

(1)

依据ECI坐标系之间的推导关系，计算出速度矢量和位置矢量由式(2)和式(3)表示

r0=rcosf·p0+rsinf·q0

(2)

(3)

式(2)和式(3)中，E为偏近点角；p0和q0分别为x轴和y轴的单位向量，以这些向量可以表示出轨道倾角i、升交点赤经Ω和近地点幅角ω，具体函数表达式如式(4)所示

(4)

由式(4)推导得式(5)

(5)

式中，h0为积分矢量，再联系惯性轨道公式间的转换关系，推出式(6)

(6)

在式(6)的基础上计算得到式(7)和式(8)

(7)

(8)

式(8)中，μ为引力常量，为定值；向量e0的表示向量为e0(ex，ey，ez)，故结合向量模计算规则计算可得离心率表达式(9)

(9)

联立上述推导出的算式，利用圆锥曲线之间半长轴a与h的关系，得到半长轴与近地点幅角表达式(10)和式(11)

a=h2/(μ(1-e2))

(10)

ω=arctan(ez/sini(eysinΩ+excosΩ))

(11)

引入升交点角距u，通过式(12)表示

u=arctan(z/(ysinΩ+xcosΩ)sini)

(12)

再由式(13)算出真近点角f

f=u-ω

(13)

根据真近点角与偏心率之间的关系，得到偏近点角E由式(14)表示

(14)

将以上计算出的相关表达式联立，再结合开普勒方程，推出平近点角由式(15)表示

M=E-e·sinE

(15)

综上，根据计算得到所需要使用到的全部轨道六根数参数，整理后如表2所示。

表2 轨道六根数

2 遗传算法

根据达尔文的自然进化理论，集群内有三种进化形式:适者生存、杂交和突变。相应的遗传算法称为选择、交叉和变异。遗传算法利用这三种形式寻找最优解。本文将以遗传算法的理论和应用展开研究。

2.1 遗传算法概念

遗传算法(Genetic Algorithm)又称为GA算法[24]，它的使用规则类似于概率进化算法，其核心思想引自达尔文的自然进化理论。利用遗传算法通过个体编码的方式代替聚类中的个体，并利用适应度函数研究聚类中问题的约束，最终实现对其遗传机制的模拟和仿真。图3所示为遗传算法概念流程图[25]。

图3 遗传算法概念流程图

2.2 遗传算法应用

在利用遗传算法优化卫星星座设计时，需要对卫星星座群中的卫星个体进行编码和建模[26]。如果星座内含有卫星总数为Kmax，则卫星星座集群内轨道建模后染色体情况如图4所示。

图4 卫星星座集群轨道染色体图

图4中的物理符号与1.3节推导出的6个轨道根数的含义相同，编码规则是从第一颗星到第K颗星。这样编码后星座染色体长度即星座卫星数如式(16)所示

(16)

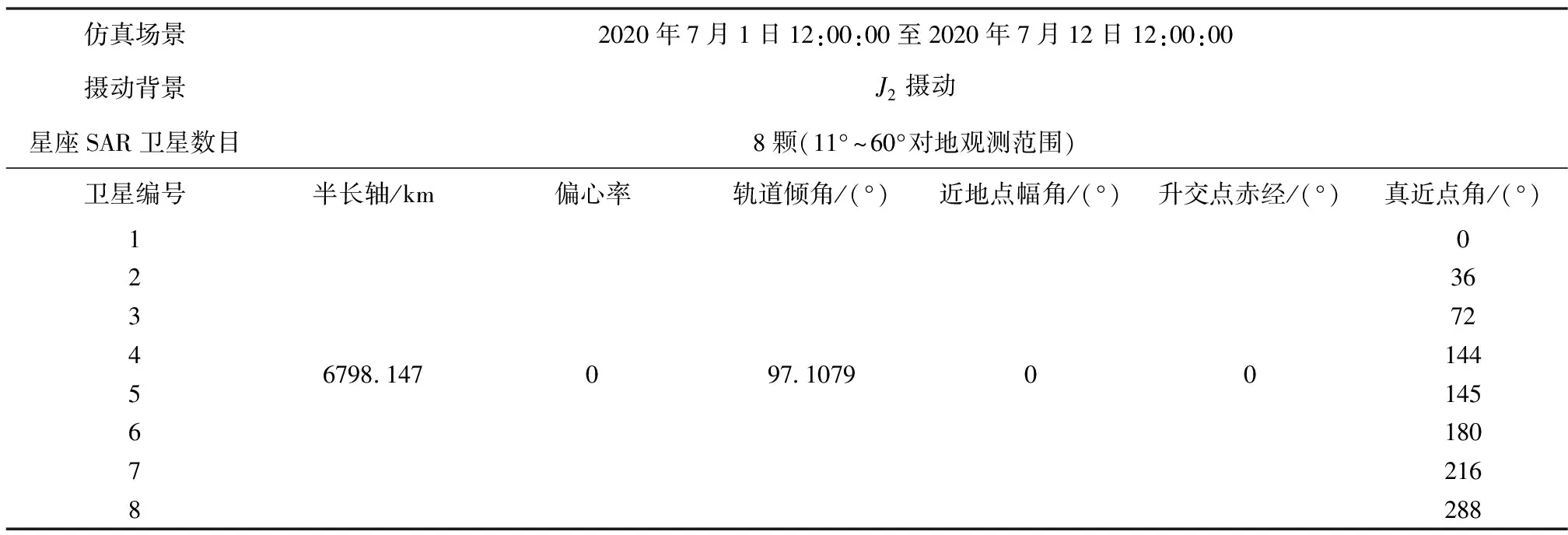
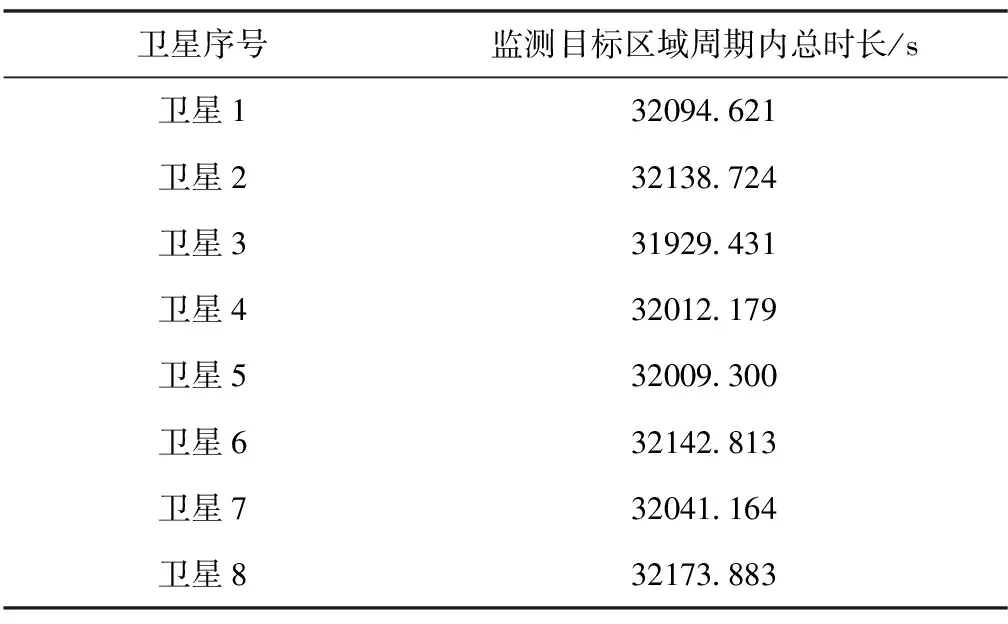
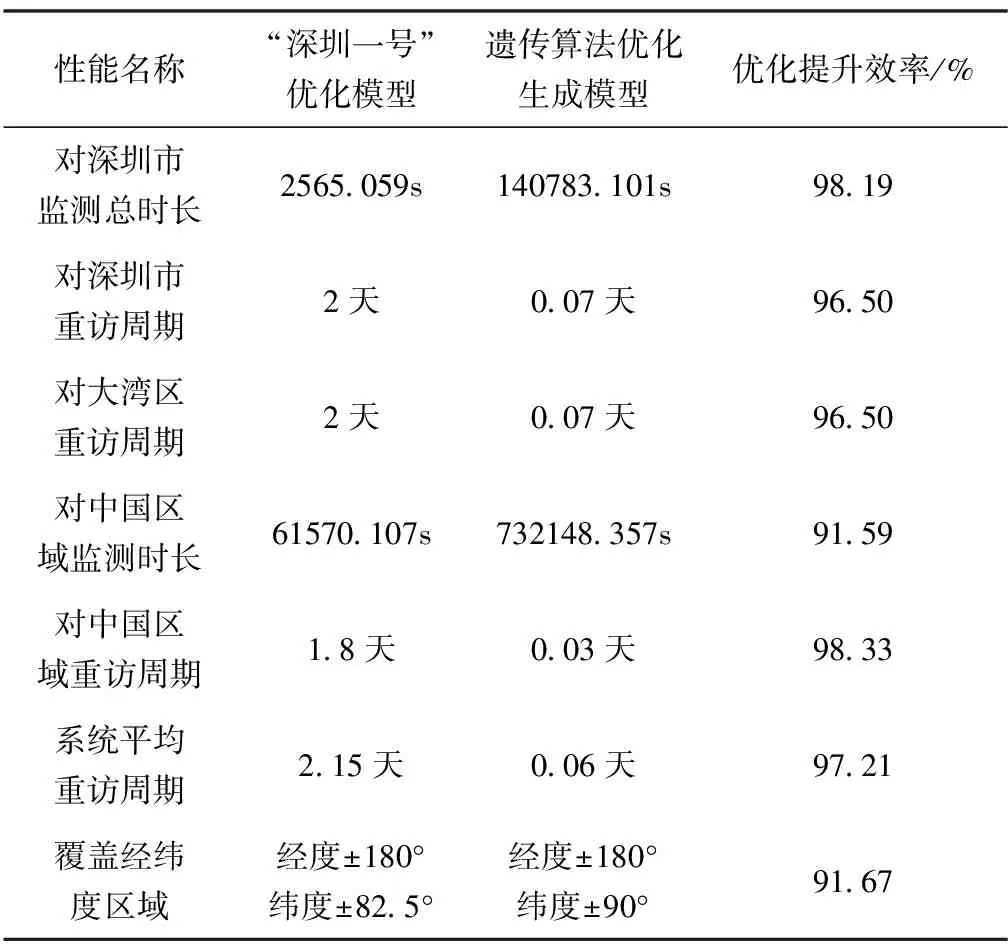
假设该优化方案中卫星星座的总周期为T，总周期内的卫星数为SNum。卫星在星座中执行命令的选择顺序是根据周期中的开始时间到结束时间来安排的。换句话说，当Ti

TSNumi≪TSNumj

(17)

其中，≪表示式子中左边的顺序在右边之前。当星座内所有卫星个体被有序排序后，有集合TASN，如式(18)所示

TASN={TSNum1,…，TSNumSNum}

(18)

式(17)和式(18)推导关系满足式(19)

i

(19)

在遗传算法的编码个体算法组中，GE、时间周期和资源等可以表示为一个算法组，其中GE为单个卫星的编码集，即周期时段内个体编码能对应相同卫星任务下的个体编码，为1×SNum维数学向量，是一个有序的排列组合，以式(20)表述

GE=[5,4,3,2,1],SNum=5

(20)

其中，GE为卫星个体编码集合，GE内的编码顺序也决定了面向任务中的排列顺序，如式(21)所示

TSeq={TGE1,TGE2,TGE3,TGE4,TGE5}

={TGE5,TGE4,TGE3,TGE2,TGE1}

(21)

式(21)的含义是，当集群内的卫星个体被编码后，即便打乱个体的排列组合，也能准确地在集群中寻找到其对应的卫星星座个体。

以上工作全部完成后，引入适应度函数F[27]，函数F包含对卫星星座轨道模型计算方面的约束A和对卫星星座设计经济成本的约束B，在此不再深入展开两项子函数内容。两子函数共同组成卫星星座优化的适应度函数F。

2.3 遗传算法策略

按照步骤执行遗传算法策略。卫星星座优化设计的建模及算法步骤如下：

步骤1：选用实验卫星星座构型(“深圳一号”卫星星座构型)，对需要实验的星座进行前期轨道预处理(轨道参数优化调整等)；

步骤2：将卫星星座构型下的卫星进行编码建模，实现种群到个体之间的一一对应；

步骤3：引入遗传算法内的适应度函数，将轨道计算约束及资源约束函数代入函数内，生成一致约束函数,通过前步骤处理和后续算法，在卫星星座整体范围内寻找最优单星解，即对目标区域和范围重访周期更短、观测范围更大的卫星；

步骤4：重复步骤3，寻找在集群样本内效果最好的几组单星解；

步骤:5：使用步骤4得到的几组较优解卫星个体生成Walker星座，组成最优解形成的卫星星座种群。使用最优解形成的星座种群对原观测目标进行观测，得到优化结果。

3 算法实现及实验分析

依照选定的“深圳一号”卫星星座构型，保持太阳同步轨道方案，引入摄动模型和轨道性能评判标准。执行上述操作完毕后，根据覆盖计算后取值轨道高度可优化范围内的最小值420km，图5所示为覆盖计算平面示意图。

图5 覆盖计算平面示意图

代入卫星SAR传感器11°～60°对地观测范围，优化后的卫星星座构型基本信息如表3所示。

表3 优化后的卫星星座构型基本信息表

根据表3数据优化后的卫星星座重访周期约为0.5天，星座优化后重访周期示意图如图6所示。

图6 星座优化后重访周期示意图

图6中，一竖格代表1天，不同颜色的条段代表星座内每个卫星对目标的观测时长。可以看出，一个竖格内出现两次条段，即代表卫星星座重访周期约为0.5天。

优化星座在重访周期内对中国区域的覆盖时长如表4所示。

表4 优化星座在重访周期内对中国区域覆盖时长表

根据优化算法的使用步骤，利用遗传算法中的适应度函数得到一组帕累托解(Pareto)[28-30]，然后通过式(16)中的编码方法，根据染色体编码的FLAG性质选择得到的解卫星个体。一组卫星解对应一个星座所有构型的基本轨道参数，包括重访周期、观测范围的经纬度和经纬度覆盖率等。表5所示为通过遗传算法获得的星座中较好的卫星个体解。

表5 遗传算法得到的星座内较好卫星个体解

其中，W1卫星是深圳为主的大湾区重点监测建设单位的最优单星方案，利用W1卫星生成的Walker星座实现对大湾区目标的精准监测和覆盖。W2卫星和W3卫星是较好的单星，可以帮助W1卫星生成的星座弥补监测缺失的区域，它们生成的Walker星座也扩大了对全球范围内目标的监测与覆盖。

因此，通过遗传算法构造个体编码下的适应度函数，并结合之前的知识得到优化方案，即在每个轨道平面有8颗卫星的前提下，使用3个Walker星座生成6个轨道平面的48颗卫星。遗传算法优化后的卫星星座构型详细参数如表6所示。

表6 遗传算法优化生成的卫星星座构型详细参数表

根据表6卫星星座构型仿真，得到使用遗传算法优化生成卫星星座的重访周期为0.07天，如图7所示。

图7 遗传算法优化生成卫星星座的重访周期示意图

图7中，一竖格代表1天，不同颜色的条段代表星座内每个卫星对目标的观测时长。可以看出，一个竖格内出现非常稠密的周期条段，通过辅助软件STK读出卫星星座的重访周期约为0.07天。

在改变参数配置优化模型的基础上，利用遗传算法得到由上述最优解组成的卫星星座优化模型。将模拟实验得到的所有数据与“深圳一号”优化基础模型的数据统计结合在同一表中进行对比分析，如表7所示。

表7 采用遗传算法得到的优化模型与“深圳一号”优化模型性能对比表

表7中，“深圳一号”优化模型列下的数据表示“深圳一号”卫星星座对目标区域及全球区域的观测数据；遗传算法优化生成模型列下的数据表示基于遗传算法优化后的“深圳一号”卫星星座对目标区域及全球区域的观测数据。由仿真实验结果并对比两列数据得知：

1)采用遗传算法生成的优化星座整体重访周期大幅缩短，对深圳市、大湾区及中国区域重访周期大幅缩短。

2)采用遗传算法优化生成的星座对空间范围实现无缝覆盖，经纬度优化效果达到数值范围内的最大值，实现100%经纬度覆盖。

3)采用遗传算法策略可以使“深圳一号”卫星星座对目标区域及全球区域的整体观测效率提升90%以上。

4 结论

1)讨论了J2摄动因素影响，对星座内卫星的轨道模型进行论证分析，结合遗传算法的个体编码和适应度函数，对“深圳一号”原模型的卫星星座进行优化，使基于“深圳一号”卫星星座构型优化模型的观测效果优于原星座模型的观测效果。

2)全面地提升卫星星座的覆盖性能，提高整体效率和观测效果，使整个卫星星座更具合理性、多样性和鲁棒性等。

3)采用遗传算法优化生成的卫星星座对空间范围实现无缝覆盖，经纬度优化效果达到数值范围内的最大值(即全球观测覆盖)。优化后的“深圳一号”卫星星座对目标区域及全球区域的整体观测效率提升90%以上。