改进的卷积神经网络及在地层识别中的应用
肖 红,张瑶瑶*,张福禄
(1.东北石油大学 计算机与信息技术学院,黑龙江 大庆 163318;2.东北石油大学 电气信息工程学院,黑龙江 大庆 163318)
0 引 言
深度学习能够有效地从原始输入数据中提取抽象且具有良好泛化能力的特征表示[1],卷积神经网络就是其代表算法之一,在计算机视觉中的图像分类[2]、图像语义分割[3]、目标检测[4]等方面取得了突破性的成功。
地层识别是在一个油区范围内对全井段地层信息进行处理[5],结果直接影响后续测井解释和储层评价的准确性[6]。众多学者利用测井曲线形态进行地层识别研究[7]。近年来,聚类分析[8]、BP神经网络[9]、贝叶斯判别[10]等人工智能算法也逐渐应用于油气勘探工作中。
卷积神经网络的原理[11]与人工地层识别中对测井曲线的特征提取与分析有相通之处,利用卷积神经网络开展自动化地层识别具有广阔的应用前景。因此,文中基于深度卷积Ghost模块,利用扩张卷积构造双向级联网络,对不同尺度特征信息进行交换,有效提高地层识别的准确率。
1 预备知识
1.1 Ghost模块
卷积操作提取的特征图冗余严重且计算成本大。Ghost模块[12]通过卷积得到部分特征图,基于已存在的特征映射,运用低成本变换得到其他可以充分揭露内在特征信息的相似特征图,既可以减少模型参数量,也可以减少模型运算量,提高网络性能。Ghost模块结构如图1所示。
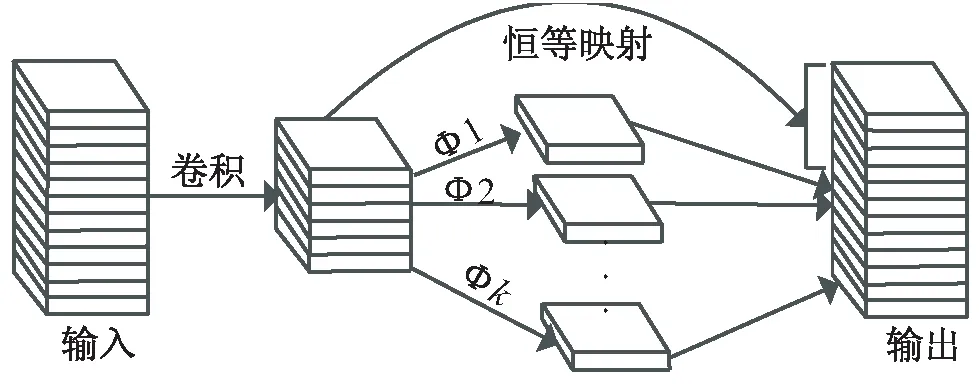
图1 Ghost模块
在搭建网络时,文中将Ghost模块组成Ghost瓶颈结构。步长为2时增添深度可分离卷积结构。与使用1*1大小点卷积的MobileNets[13]、Shufflenet[14]等模型相比,Ghost瓶颈结构中可以自定义卷积核大小。以前模型架构[15-16]处理特征图的操作仅限于深度卷积或移位操作,而Ghost瓶颈结构恒等映射与线性变换并行进行,从而保留固有特征图。
1.2 扩张卷积
文中欲搭建的网络需要具有聚合多尺度信息能力,而扩张卷积[17](dilated convolution,Dconv)可以在不丢失分辨率或者重新缩放图像的前提下,聚合多尺度上下文信息。其原理如下:
设F:Z2→R为离散函数。令Ωr=[-r,r]2∩Z2并令k:Ωr→R是(2r+1)2的离散滤波器。离散卷积运算*可以定义为:
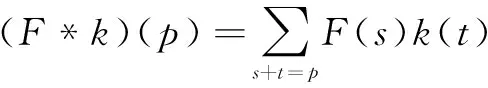
(1)
设l是扩张因子并定义:
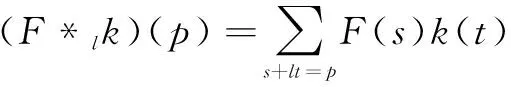
(2)
*l为扩张卷积或者扩张l倍的卷积,常见的卷积操作是扩张1倍的卷积。
设F0,F1,…,Fn-1:Z2→R为离散函数,令k0,k1,…,kn-2:Ω1→R为离散的3×3滤波器,使用扩张因子滤波器:Fi+1=Fi*2iki(i=0,1,…,n-2),定义Fi+1中元素p的感受野作为F0的一组修改为Fi+1(p)的元素,设Fi+1中p的感受野的大小为这些元素的数目。显而易见,Fi+1中每个元素的感受野的大小是(2i+2-1)×(2i+2-1),有效增加了感受野范围。
1.3 双向级联网络结构
双向级联网络(bi-directional cascade network,BDCN)[18]的双向损失函数监督学习模式在每一层中负责监督训练,使每一层都集中在一个特定的尺寸上,并对所有层输出进行融合。
在BDCN中,假设Y是边缘标签,标签可以分为小部位边缘和大部为边缘,即边缘标签中存在很大的尺度变化,那么Y可以分解成多种尺度的叠加:
(3)
其中,YS是某一个特征的尺度的标签。
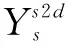
(4)
其中上标s2d表示从浅层到深层的传播,d2s表示从深层到浅层的传播。
2 双向级联GhostNet模型
2.1 网络模型结构
多尺度表示对于地层识别至关重要,文中设计了利用扩张卷积生成多尺度特征,并利用BDCN自动学习不同图层中的尺度的网络模型—双向级联GhostNet。双向级联GhostNet网络的多个ID block通过双向级联结构推断出不同的监督来学习。具体而言,该网络基于GhostNet,在其第二层添加一个卷积层,然后将GhostNet中的13个卷积层分成6个区块,每个区块遵循一个汇集层,逐步扩大下一个区块中的感受域。其具体结构如图2所示。
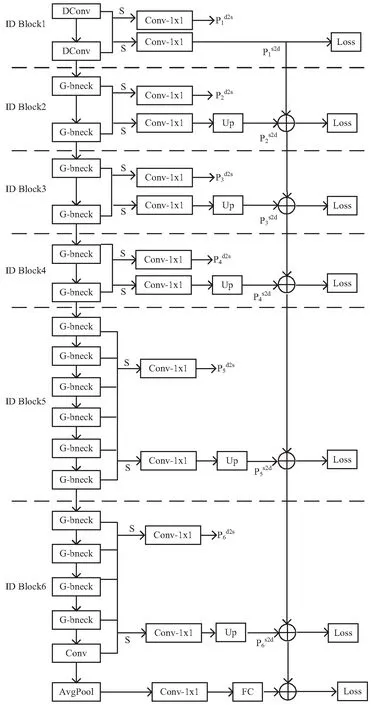
图2 双向级联GhostNet结构
2.2 运算关系
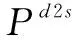
2.3 计算效率
对于给定数据X∈Rc×h×w(c、h和w分别表示输入数据的通道数、高和宽),任意卷积层生成n个特征图的运算可表示为:
Y=X*f+b
(5)
其中,*表示卷积操作,b表示偏量,Y∈Rn×h'×w'表示n通道的输出特征图(h'和w'表示输出数据的高和宽),f∈Rc×k×k×n表示在此卷积层的卷积滤波器(k×k表示卷积滤波器的内核大小)。
卷积操作过程的浮点运算数为nh'w'ck2,通常多达数十万。根据等式(5)可知,f和b中需要优化的是输入和输出特征图的尺寸。假设输出特征图是通过廉价操作得到的固有特征映射的相似图,固有特征图由普通的卷积滤波器生成。M个固有特征映射Y'∈Rm×h'×w'通过使用一次卷积:
Y'=X*f
(6)
为简单起见,省略了偏置项。根据Y'上的固有特征生成相似特征图:
(7)

(8)
其中,d×d的大小与k×k的大小相似,而s< (9) 由此可见,使用Ghost模型,能够减少卷积计算中的冗余,有效提高计算速度。 测井曲线是地质勘探人员对复杂矿场情况进行观测和分析的有效措施。文中结合专家经验、油藏描述等专业相关知识,进行测井曲线组合优选,并通过数据分层、沃尔什滤波以及分段线性插值等方法对数据进行预处理,将测井曲线形态转换为二值图像,构建样本数据集,并运用卷积神经网络进行识别。操作流程如图3所示。 图3 地层识别方法流程 在实际地层对比工作中,收集选定的油田区域每口井的测井曲线作为原始数据,但不同的测井曲线对地层对比的贡献程度不尽相同。例如,筇竹寺组具有极高自然伽马和低电阻率的特性,而灯四段伽马低值,曲线近乎平直,偶夹小齿状,电阻率高值。此外,不同油田区域具有不同的地质环境,因此在进行地层识别研究时,需要根据地区特性来进行测井曲线组合优选,有利于构造高质量的训练样本,从而提升网络的训练效率和泛化能力。 实际测井曲线存在尖锐点、每层的数据点个数不同等问题,为解决这些问题,在构建训练集前,选用沃尔什滤波对数据进行异常点清洗,并采用分段线性插值法将每层数据点个数统一化。 3.2.1 沃尔什滤波 为避免数据在测井过程中因设备或信号等原因产生异常点,对最后分类准确率产生影响,文中采用沃尔什滤波对所有测井曲线片段进行处理,剔除异常点。 沃尔什滤波变换核为: (10) 其中,bk(z)为z的二进制第k位值。 设f(x)为离散序列,沃尔什滤波变换表示为: (11) 其中,u=0,1,…,N-1;N=2n。 沃尔什滤波反变换核为: (12) 沃尔什滤波反变换公式为: (13) 3.2.2 分段线性插值 为解决小层厚度不相等问题,统计各小层数据点个数,根据统计结果统一数据点个数为L,对少于或多于此长度的测井曲线片段分别进行插值和抽稀操作。为避免高次插值在插值区间边界产生剧烈动荡,文中采用分段线性插值法进行插值与抽稀。 原理如下: 设已知节点a=x0 (14) 满足φ(xi)=yi,其中i=0,1,…,n,且在每个小区间[xi,xi+1](i=0,1,…,n)上φ(x)是线性函数。 3.3.1 样本图像构造方法 3.3.2 实施网络训练 采用样本图像构造方法,将测井曲线形态转换为二值图像,对不同地层的图片进行类别标注,分别记为1-7,并将样本图像随机划分为训练数据集和测试数据集。网络参数包括:训练迭代次数、每次输入网络的样本数量、初始学习率、动量因子、权重衰减因子等。采用Adam优化方法对网络进行多次重复训练,直到对测试集样本达到满意的识别率,训练结束。经过训练后的网络可以直接用于未知类型的地层识别,具体方法为:将未知类型地层的特征数据预处理为与训练样本相同的图像,直接提交训练后的网络,根据网络输出即可判定类别。 实验数据来自西南盆地,文中主要研究层段为:龙王庙、沧浪铺、筇竹寺、灯四2、灯四1、灯三段以及灯二段,共计7个地层。 根据已有地质结构资料来评估测井曲线组合特征和已知地层划分之间的对应关系,通过分析对比,文中选择对地层识别影响较大的五种测井曲线:声波时差(AC)、补偿中子(CAL)、自然伽马(GR)、梯度电阻率(RT)以及自然电位测井曲线(SP)。本次数据共包含739口井,每口井优选5条测井曲线,每条曲线分为7层,根据小层起始深度和终止深度对测井曲线进行分层,分层后获得25 865个曲线片段。 为解决测井曲线异常点波动过大问题对矿场数据的25 865个曲线片段进行沃尔什滤波,沃尔什滤波变换系数设置为1。对小层数据点个数进行统计,取平均值1 000为统一数据点个数。对于少于此数值的小层曲线进行插值,多于此数值的小层曲线进行抽稀。部分数据处理前后如图4所示,original离散点表示原始数据,数据点个数大于统一值,对数据采用分段线性插值原理进行数据抽稀;interpolation离散点表示对数据进行抽稀后得到的结果,数据量虽减少但仍可保持曲线形态;Walsh filtering离散点表示进行沃尔什滤波后的曲线形态,曲线尖锐部分变得平滑。 图4 数据处理前后对比 根据曲线统计结果可得,五种曲线的最大值和最小值分别为Maxi∈{585,44,115,1 106,100}、Mini∈{0,0,0,0,-116},构造大小为1 000*3 325像素的0值图像,为保证图片大小适中,对曲线等比例缩放,最终图像大小为1 000*1 000像素,依次将5条测井曲线片段映射到对应位置,共获得5 173张映射图,七层地层曲线形态图如图5所示。随机选择80%测井曲线数据作为训练集,20%作为测试集。 图5 测井曲线映射图 网络采用pytorch框架,Linux操作系统下应用Nvidia RTX 2070 GPU进行编译、训练及测试。 GhostNet、扩张卷积GhostNet和双向级联GhostNet初始学习率分别为0.4、0.1和0.1,学习率每迭代30次减少10倍,权重衰减因子为0.000 1,Nesterov动量因子为0.9。GhostNet使用随机梯度下降优化算法,扩张卷积GhostNet和双向级联GhostNet使用Adam优化算法。训练迭代次数为250,批量大小为64。GhostNet损失函数结果如图6(a)所示,扩张卷积GhostNet损失函数结果如图6(b)所示,双向级联GhostNet网络的损失函数结果如图6(c)所示,网络参数量及测试集上的准确率如表1所示。 (a)GhostNet损失函数下降曲线 (b)扩张卷积GhostNet损失函数下降曲线 (c)双向级联GhostNet损失函数下降曲线 表1 地层识别准确率 为了验证文中方法相比现有方法的优势,与MobileNetV3、ResNet34进行对比实验。ResNet34优化器为均方根传播优化算法,初始学习率为0.045,每迭代2次后以0.94的指数速率衰减。MobileNetV3使用相同优化算法,动量为0.9,初始的学习率为0.1,每3个迭代学习率因子衰减0.01。 实验结果如表2所示,改进后的网络在地层识别上的准确率分别高达96.67%,比同类算法平均提升6.18%,且参数量较少。 表2 同类方法地层识别准确率 对于文中模型在地层识别问题中所展示出的优势,给出如下理论分析。首先,由损失函数下降曲线图可知,GhostNet损失函数值下降,但曲线震荡,网络在学习过程中可能遇到瓶颈。随后,将普通卷积替换为扩张卷积,有效提高了网络的学习与泛化能力,损失函数下降曲线收敛速度较快。最后,双向级联GhostNet每一层的双向监督机制,解决了训练策略的问题,网络收敛效果较好,网络特征提取能力增强,得到稳定的性能提升。 文中提出了一种双向级联GhostNet的新方法,并将其应用于实际地层识别中。首先,更改GhostNet模块中的普通卷积为扩张卷积,从而获得多尺度表示;其次,构建双向级联网络,使用双向损失函数对学习过程进行监督,增强识别准确性;最后,将测井数据进行预处理,将测井曲线形态转化为二值图片,构造样本数据集,使用样本图像进行网络训练及测试。实验结果表明,该方法不仅具有较高的地层识别准确率而且网络参数量较少,优于同类的对比方法,从而表明提出的改进措施是有效的、可行的。3 基于双向级联GhostNet的地层识别方法
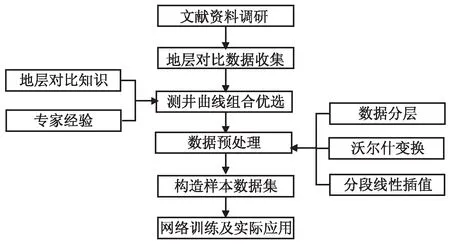
3.1 曲线组合优选
3.2 数据预处理
3.3 基于双向GhostNet模型的网络训练
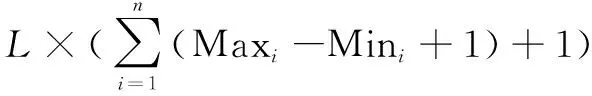
4 实验及结果分析
4.1 资料数据
4.2 数据处理

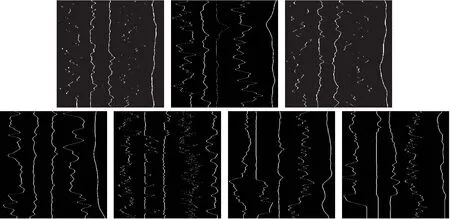
4.3 构造样本图像
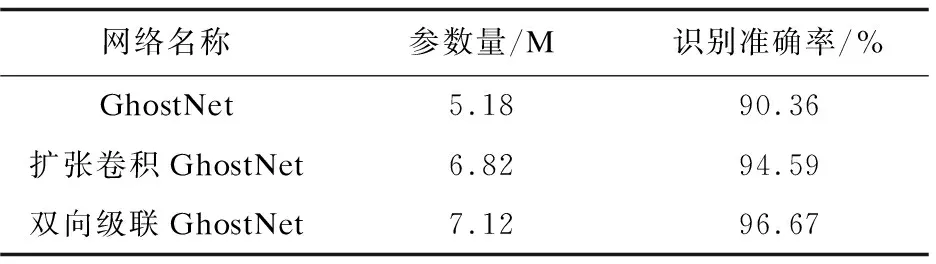
4.4 比较分析
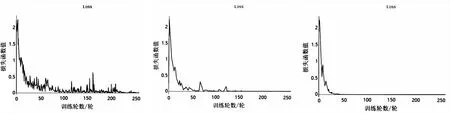
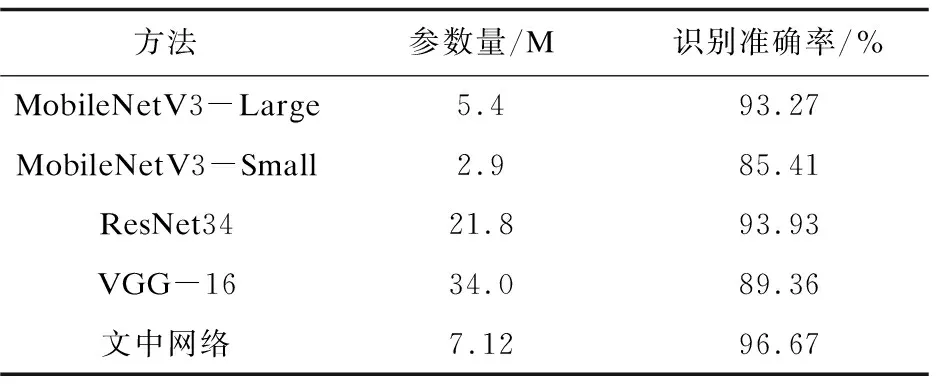
5 结束语

