基于改进海鸥算法的认知无人机网络频谱分配

岳文静，孙 鹏，陈 志

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210023;2.南京邮电大学 计算机学院，江苏 南京 210023)

0 引 言

无人机由于其多功能性，在军事、私人和公共部门越来越受青睐。无人机运行在工业、科学和医学等波段，但随着在这些频段运行的无线和蜂窝网络的新设备的开发和使用急剧增加，且频谱利用率低下，无人机可用频谱资源急剧减少。认知无人机网络通过将无人机与认知无线电技术结合可以感知主用户未使用的频段，通过频谱资源分配获得可用的频谱资源，从而解决无人机频谱资源短缺的问题，提高频谱利用率[1]。在多无人机频谱接入和认知无线电方面，国内外研究人员进行了大量的研究。文献[2]将认知无线电最优频谱问题归结为图着色问题的变体，提出基于图着色理论的认知无线网络频谱分配模型。文献[3-5]将博弈论应用于频谱接入中，获得了较高的系统吞吐量和效用。文献[6]提出了一种基于后悔博弈的ABS和蜂窝/WiFi共存网络的动态传输占空比分配方案。有些研究人员将智能优化算法用于频谱分配中，获得了较好的效果。

例如文献[7]将改进的乌鸦算法用于车载网频谱分配。文献[8]使用遗传算法进行频谱分配，文献[9]提出一种改进的量子遗传算法并将其用于频谱分配。文献[10-11]采用粒子群优化算法进行频谱分配。文献[12]提出了一种新的二元自适应布谷鸟搜索算法，该算法在传统布谷鸟搜索初始化阶段引入了反向学习，增加了布谷鸟搜索的多样性。文献[13]提出了一种多策略DSA(MS-DSA)系统，其中主系统和辅助系统同时使用多种DSA策略共享频谱资源，并证明通过所提出的MS-DSA系统可显著改善性能。文献[14]提出了一种用于CR网络的双拍卖框架，该框架解决了信道分配问题，以提高频谱利用率，与McAfee拍卖相比，网络模拟验证了所提议拍卖模型的改进性能。

然而以上这些算法在算法寻优能力和收敛速度上没有较好的平衡，遗传算法虽然具有很好的全局搜索能力，但是局部搜索能力较差；粒子群优化算法求解速度较快，但是容易出现早熟收敛等问题；蚁群算法在求解性能上具有很强的鲁棒性和搜索较好解的能力，但是收敛速度慢，易于陷入局部最优；布谷鸟算法对参数不敏感，鲁棒性强，但是求解速度慢。Gaurav Dhiman和Vijay Kumar在2018年通过模拟海鸥的迁徙和攻击行为来实现寻优，提出海鸥优化算法[15]。基于此，文中提出一种基于改进海鸥优化算法的认知无人机网络频谱分配方案，可以在保留优良个体的同时维持种群多样性。结果表明，该算法在认知无人机网络频谱分配具有较好的性能。

1 认知无线电网络频谱分配模型

1.1 基于图着色理论的认知无线网络频谱分配模型

图着色认知无线网络频谱分配模型[2]将认知无线电最优频谱问题归结为图着色问题，考虑了可用频谱范围集合形成频谱池，划分成互不重叠的正交信道的情况。每个次用户根据频谱感知的结果获得其可以使用的可用信道列表，并调整自身的发射功率，而不会干扰相邻的主用户，频谱接入问题变成了信道分配问题。假设共有M个主用户，M个信道，N个次用户，图着色频谱分配模型可以表示为：

(1)可用频谱矩阵L：ln,m=1时次用户n使用信道m不会干扰主用户。相反则表示会干扰主用户m。

L={ln,m|ln,m∈(0,1)}N×M

(1)

(2)频谱效益矩阵B：bn,m表示次用户n使用信道m可以获得的最大带宽或吞吐量，B与L有关，当ln,m=0时bn,m=0。

B={bn,m}N×M

(2)

(3)干扰约束矩阵C：cn,k,m是次用户n和k同时使用信道m时的干扰约束。cn,k,m=1时次用户n和次用户k同时使用信道m会相互干扰，此时需要n或k放弃使用信道m。cn,k,m=0时次用户n和k同时使用信道m不会相互干扰，此时n和k可以同时使用信道m。cn,k,m受矩阵L影响，cn,k,m≤ln,m×lk,m且cn,n,m=1-ln,m。

C={cn,k,m|cn,k,m∈(0,1)}N×N×M

(3)

(4)无干扰分配矩阵A：表示次用户不影响主用户且次用户之间不产生干扰时的信道分配。an,m=1表示将信道m分配给次用户n，反之，表示信道m未分配给次用户n。无干扰分配矩阵A取决于矩阵L和矩阵C。当ln,m=0时，an,m=0。当cn,k,m=1时，an,m×ak,m=0。

A={an,m|an,m∈(0,1)}N×M

(4)

(5)用户效益：表示次用户的用户效益集合，βn表示次用户n可以获得的用户效益。

(5)

(6)总用户效益：表示所有次用户获得的总效益。

(6)

(7)解向量的维数l，表示可用频谱分配矩阵中1的个数。

(7)

1.2 认知无人机网络频谱分配模型

假设在一个区域内分布着M个信道，每个信道被单独分配给一个主用户，这M个主用户和N个无人机用户在区域内随机分布，无人机用户通过频谱感知获得区域内可用信道，并将获取的信息反馈给基站，由基站进行信道分配。

图1是在信道m下主用户和无人机用户信号距离关系示意图，圆形表示用户信号覆盖范围。dp(x,m)表示主用户x使用信道m时的保护范围。dist(b,x)表示无人机用户b与主用户x的距离，ds(a,m)表示无人机用户a在使用信道m时的覆盖范围，无人机用户可以控制自己的功率改变覆盖范围，避免干扰。

设主用户x坐标为(xpu,ypu)，无人机用户n坐标为(xsu,ysu)，主用户和无人机用户之间距离为：

(8)

由感知到的频谱信息可以获得可用频谱矩阵L、干扰约束矩阵C以及频谱效益矩阵B。当ln,m=1且cn,k,m=0时说明无人机用户n可以使用信道m，此时无人机用户n使用信道m的传输速率bn,m可以表示为：

bn,m=ds2(n,m)

(9)

ds(n,m)=min{dmax,dist(n,x)-dp(x,m)}

(10)

其中，dmax表示无人机用户使用最大发射功率时信号的覆盖范围。

总用户效益可以表示为：

(11)

2 基于海鸥优化算法的认知无线电频谱分配

在迁徙过程中，海鸥会结伴而行，海鸥的初始位置是不同的，以避免彼此之间的碰撞。在一个群体中，海鸥可以朝着生存最好、最健康的海鸥的方向飞行，基于最健康的海鸥，其他海鸥可以更新它们的初始位置。当海鸥从一个地方迁徙到另一个地方时，它们经常在海上攻击候鸟，它们可以在攻击过程中做出螺旋形的自然运动。

2.1 基本海鸥优化算法

基本海鸥算法步骤如下：

(1)初始化种群以及参数Asoa、fc和MAXiter。

Asoa=fc-x×(fc÷MAXiter)

(12)

Asoa用于计算新的海鸥位置，从fc降到0，fc是控制Asoa的参数，MAXiter是最大迭代次数，x是当前迭代次数。

(2)计算所有海鸥的适应度值，输出最佳海鸥的位置Pbest(x)。

(3)计算不与其他海鸥存在位置冲突的新位置Cs(x)。

Cs(x)=Asoa×Ps(x)

(13)

其中，Ps(x)表示海鸥当前的位置。

(4)计算最佳位置所在的方向Ms(x)。

Ms(x)=Bsoa×[Pbest(x)-Ps(x)]

(14)

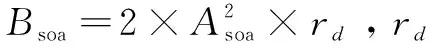
(5)计算海鸥和最佳海鸥之间的距离Ds(x)。

Ds(x)=|Ms(x)-Cs(x)|

(15)

(6)计算海鸥的新位置。

Ps(x+1)=Ds(x)×x×y×z+Pbest(x)

(16)

其中，x、y、z表示海鸥在空间中的运动行为x=r×cosθ，y=r×sinθ，z=r×θ，r=u×eθv,θ是0到2π的随机值。

(7)更新并输出最佳海鸥位置和适应度值，如果当前海鸥适应度值大于最佳海鸥适应值，用当前海鸥的适应度值代替最佳海鸥适应度值，用当前海鸥位置代替最佳海鸥位置。

(8)判断当前是否达到最大迭代次数，如果达到执行步骤9，否则返回步骤2。

(9)输出最佳海鸥位置和适应值。

2.2 改进海鸥优化算法

2.2.1 克 隆

克隆操作的基本思想来源于免疫系统，通过克隆将原始种群的个体进行复制生成多个镜像，可以实现个体空间的扩张，增强对解空间的搜索力度。文中采用克隆增广算子进行克隆操作，对原始种群的每个个体按照其适应度的大小进行复制，适应度大的产生较多镜像，适应度小的个体产生较少镜像，其表示如下：

Ni=s

(17)

其中，Ni表示第i个个体克隆的数量，s表示种群按照适应度升序排列后该个体的位置。

2.2.2 变 异

通过克隆变异算子在克隆的种群中进行变异操作，以在每个个体附近实现区域搜索，从而实现局部寻优。克隆变异算子定义为：

(18)

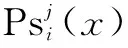
2.2.3 选 择

在变异后的个体以及原始个体中进行选择操作，以进行下一次的迭代操作。文中采用人工免疫算法中的免疫选择算子计算选择概率，使用轮盘赌的方法进行选择操作，免疫选择算子定义为：

Pc=α•Pf+(1-α)•Pd

(19)

其中，Pc为选择概率，Pf为个体的适应度概率，定义为抗体的适应度与适应度总和之比，Pd为抗体的浓度概率，抗体浓度越高越受抑制，浓度越低则越受促进，α为比例系数，决定了浓度与适应度的作用大小，0≤α≤1。

根据免疫选择算子对种群进行选择操作，选择操作如下：

(20)

其中，Psi(x)为第i个个体，cum(i)为第i个个体之前的Pc的累积概率。

海鸥算法适用于连续空间的优化求解，而文中所用到的频谱模型为二进制，需要通过sigmod函数将连续数值转换成二进制数，操作如下：

(21)

(22)

2.3 基于改进海鸥算法的频谱分配方案

(1)初始化频谱效益矩阵B、干扰约束矩阵C和可用频谱矩阵L，计算l作为解向量的维数，设置种群维数为popsize，变异概率pm，参数Asoa、fc和MAXiter。

(2)初始化种群X，并根据干扰约束矩阵C进行无干扰处理。计算所有海鸥的适应度值，输出最佳海鸥的适应值Pbest(x)。

(3)使用公式(13)-(14)计算不与其他海鸥存在位置冲突的新位置Cs(x)以及最佳位置所在的方向Ms(x)。

(4)使用公式(15)计算海鸥和最佳海鸥之间的距离Ds(x)。

(5)使用公式(16)计算海鸥的新位置Ps(x+1)。

(6)使用公式(11)对种群进行二进制转换，根据干扰约束矩阵C进行无干扰处理，计算种群的适应度并排序。

(7)根据公式(17)-(18)进行克隆、变异操作，并将变异后的个体与其克隆的种群比较，如果变异后的个体适应度比其克隆的个体适应度高，则使用变异后的个体替换原个体，否则原个体参与选择操作。

(8)计算出适应度最大的个体及其位置，适应度记为BestF，位置记为Best_pos。

(9)根据公式(19)-(22)进行选择操作，选择出的结果参加下一次迭代。

(10)比较本次迭代最大适应度与上一次迭代最大适应度，保留最优的适应度和位置。

(11)判断当前是否达到最大迭代次数，如果达到执行步骤12，否则返回步骤3。

(12)输出最佳海鸥位置Best_pos和适应值BestF。

3 算法仿真与分析

本组实验对ISOA、SOA、GA、QGA、PSO这五种算法的性能进行比较。本次实验使用MAT LAB 2018a进行仿真，取本次实验最大迭代次数MAXiter为200,变异概率pm=0.02，fc=2，α=2，u=v=1，无人机最大覆盖范围为4 km，最小覆盖范围为1 km，本次实验在10 km×10 km的区域完成。

图2是在主用户数K为10，可用信道数M为10，无人机用户数N为20的情况下认知无人机网络进行一次频谱分配的结果。由图2可知，ISOA算法在寻优性能上要优于SOA、QGA、PSO和GA算法，可以看到通过ISOA算法获得的网络效益要高于其余四种算法，SOA算法次之，GA算法得到的网络效益最低。与其余四种算法相比，ISOA具有较快的收敛速度，在寻优的过程中曲线有起伏是因为在算法中加入了变异操作，使得算法在寻优的过程中可以跳出局部寻优。

图2 一次频谱分配网络效益

由于频谱分配矩阵和初始种群是随机生成的，所以一次寻优的结果也存在着较大的随机性，图3绘制了五种算法进行30次寻优操作的平均曲线。可以看出文中所提算法明显优于其余四种算法，ISOA算法所得到的网络效益最大。

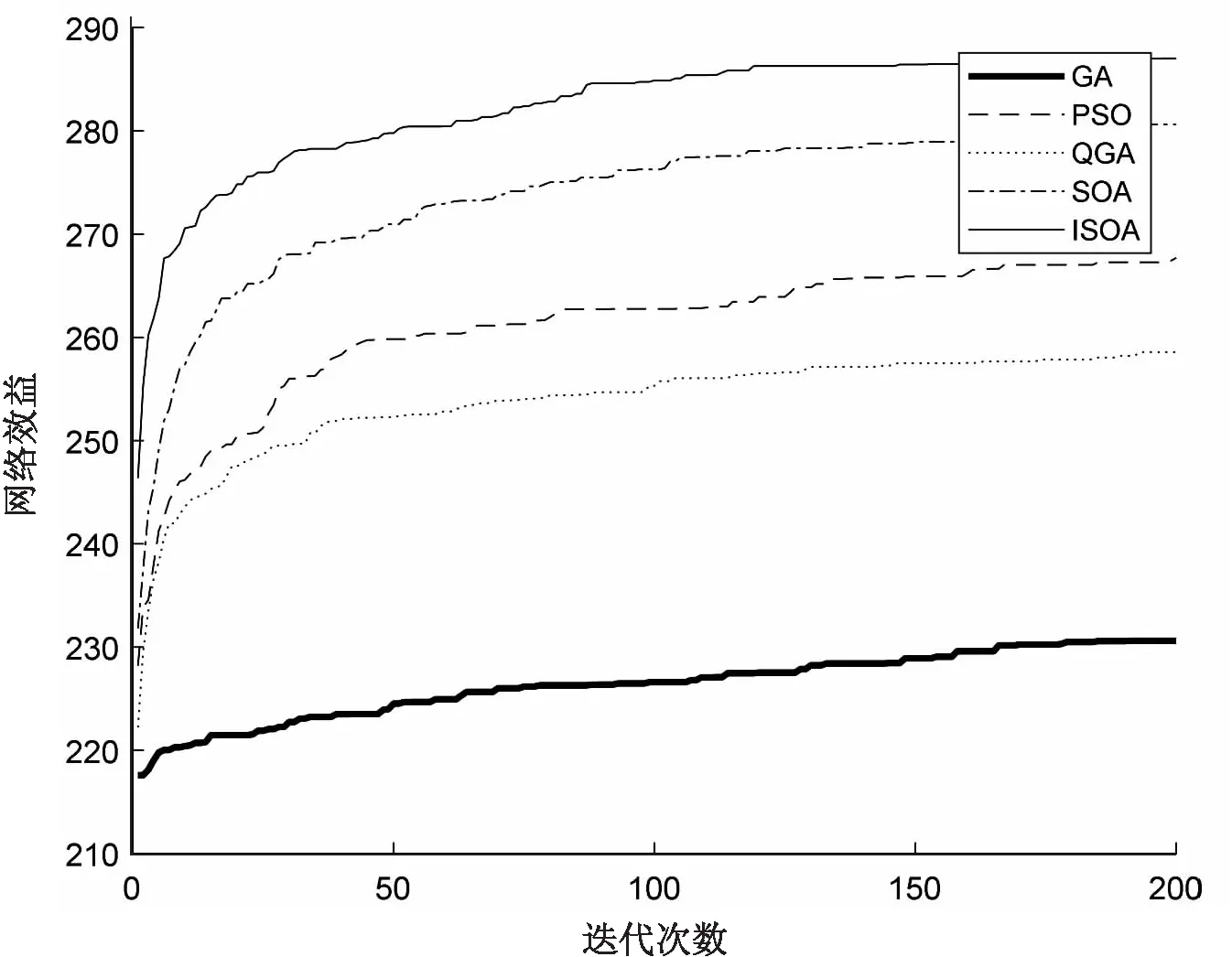
图3 30次频谱分配平均网络效益

图4是在保持无人机用户数和主用户数不变，可用信道数变化情况下30次算法运行结果的平均值仿真结果。保持次用户数N=20，主用户数K=10，可用信道数从10增长到30。可以看到随着可用信道数的增长，五种算法所获得的频谱效益也在增长，这是因为随着可用信道数的增长无人机用户可以使用的信道数也随之增长，可获得的网络效益也随之增长。

图4 可用信道数变化对网络效益的影响

图5是在保持可用信道数和主用户数不变，无人机用户数变化情况下30次算法运行结果的平均值仿真结果。保持可用信道数M=10，主用户数K=10，无人机用户数从10增长到30。由图5可知，随着无人机用户数的增加，网络效益先增加然后逐渐减小。这是由于文中网络效益是所有无人机用户效益之和，所以随着无人机用户数增多，网络效益也逐渐增大。但是由于可用信道数有限以及无人机用户和主用户之间、无人机用户之间存在干扰限制，所以无人机用户数量增加到一定数量时，网络效益开始减小。

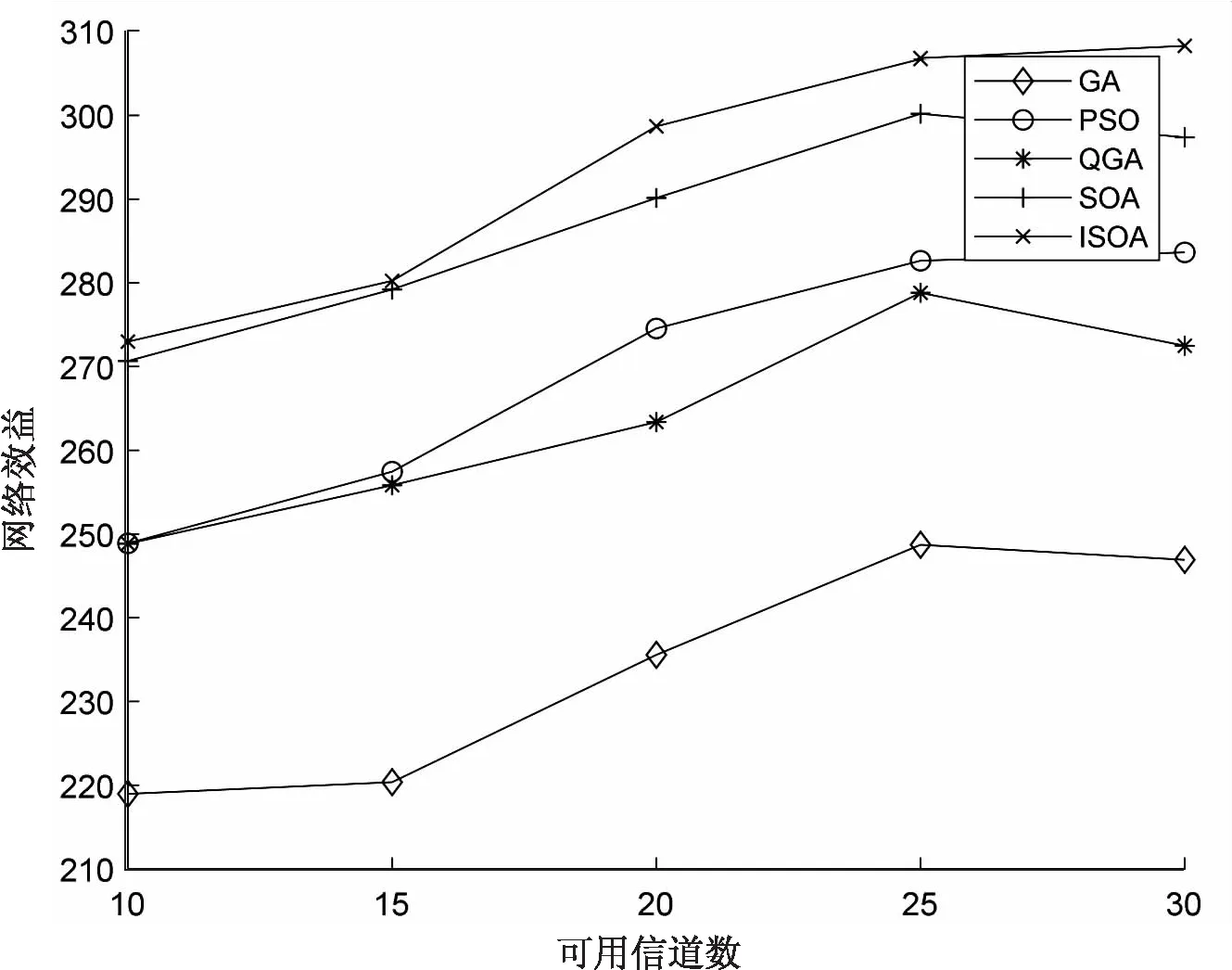
图5 无人机用户数变化对网络效益的影响

图6是在保持无人机用户数和可用信道数不变，主用户数变化情况下30次算法运行结果的平均值仿真结果。保持可用信道数M=10，无人机用户数N=20，主用户数从10增长到30。由图6可知，随着主用户数的增加，无人机用户的网络效益逐渐减下，这是由于可用信道数有限，随着主用户数增加，无人机用户和主用户之间干扰约束增强，导致无人机用户网络效益减小。

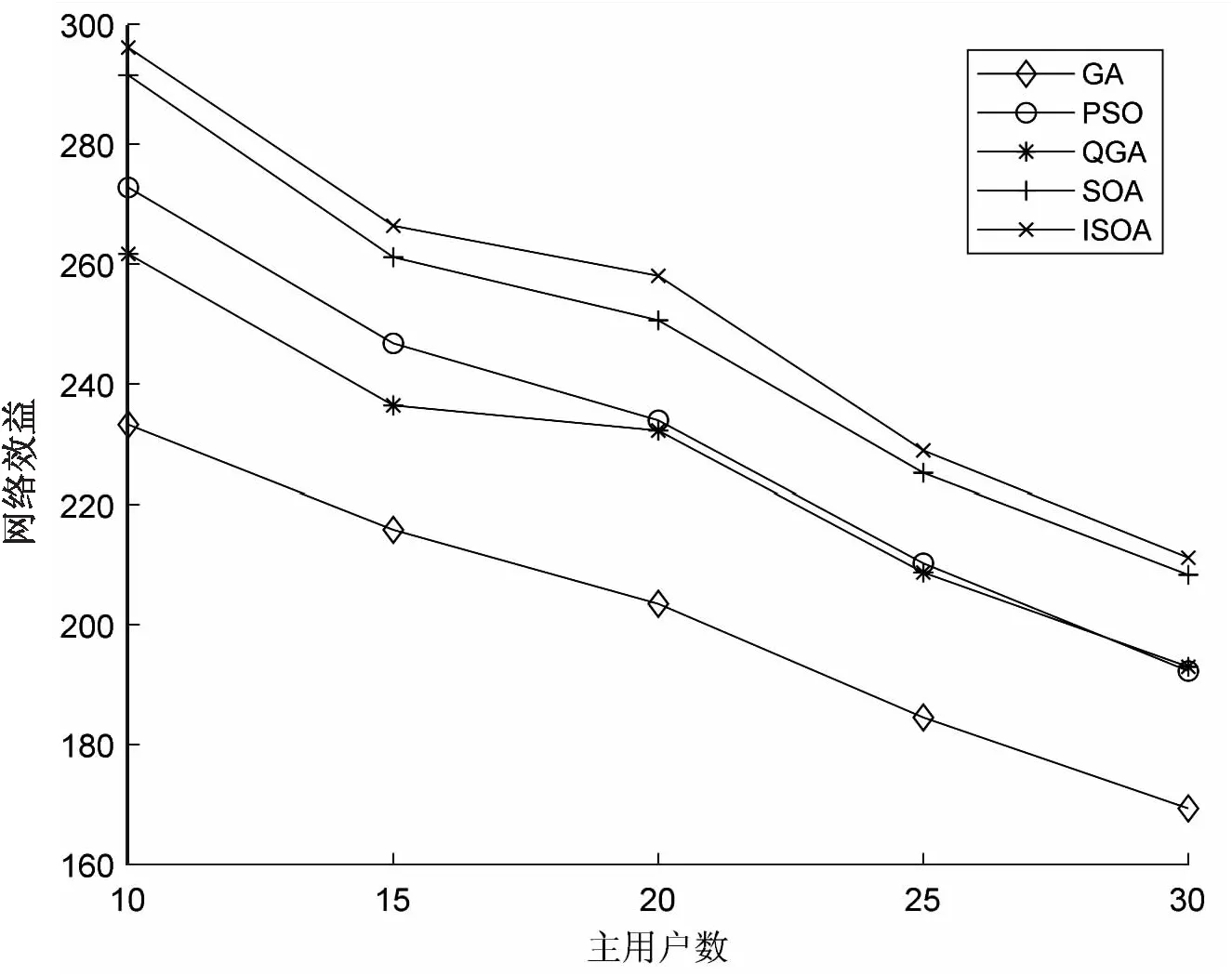
图6 主用户数变化对网络效益的影响

4 结束语

文中将海鸥优化算法用于认知无人机网络频谱分配，并提出海鸥优化算法的改进算法，将其与遗传算法、量子遗传算法、粒子群优化算法进行比较。实验结果表明，提出的改进海鸥优化算法在解决认知无人机网络频谱分配问题上要优于其余四种算法。下一步将研究无人机抗干扰以及移动情况的网络优化方案，以实现网络资源的高效利用。