基于FPGA的自适应光学系统SPGD算法实现

徐项项，吴 阳，苏 杭，刘金龙，杨慧珍,2，龚成龙

（1.江苏海洋大学 电子工程学院，江苏 连云港 222005；2.江苏省海洋资源开发研究院，江苏 连云港 222005）

引言

随机并行梯度下降算法（stochastic parallel gradient descent algorithm，SPGD）是目前被广泛应用的无波前探测自适应光学系统控制[1-6]，由美国陆军研究实验室Voronstov在同时扰动随机近似控制算法和随机逼近理论基础上开发的一种无波前探测自适应光学系统控制算法[7]。该算法无需波前传感和相位重构，系统复杂性大大降低，但算法迭代执行方式使得自适应光学系统收敛速度慢。目前SPGD算法的实现方式大致可以分为3种，一是通过软件编程在PC（personal computer）机上实现[8-9]，二是使用混合超大规模集成电路（mixedmode VLSI）[10]，三是使用FPGA（field programmable gate array）[11-12]集成电路实现[13-15]。方法1灵活，但系统收敛速度慢，工作带宽较低。方法2迭代速度快，实时性强，但硬件模拟电路复杂，成本高且不能重复编程，一旦成品无法进行修改。方法3可重复编程，算法实现灵活，且可将FPGA配置成满足需求的任何电路。但目前FPGA实现SPGD算法技术不能满足不同单元变形镜，仅适用于固定单元变形镜，降低了FPGA实现SPGD控制算法的通用性。另外，FPGA内部对串行传入的图像数据不执行矩阵恢复，最终将导致通过FPGA实现变形镜控制电压计算的不精确，影响自适应光学系统的校正能力。

本文提出把采集光斑图像灰度值以串行方式存入FPGA内部ROM核中，获取图像数据的地址位设定判断条件，通过矩阵恢复方法恢复图像数据，确保算法性能指标计算的准确性。通过改变随机序列的维数，便可满足不同单元数的变形镜需求，提高了实现方案的通用性。首先使用TimeGen软件对SPGD算法的主要功能模块进行时序分析，再利用Vivado软件完成SPGD算法的随机扰动电压生成、性能指标计算和变形镜控制电压的计算与输出，并对FPGA进行代码编写。最后将各个模块计算得到的数据与使用Matlab软件计算得到的数据进行对比分析，以验证本文所提方法的各个模块计算的合理性和准确性，为实际应用提供参考。

1 自适应光学系统SPGD算法

1.1 系统介绍

如图1所示，无波前探测自适应光学系统主要由波前校正器、图像传感器、波前控制模块等组成。带有畸变的光波经过波前校正器反射，再经透镜聚焦到图像传感器上。控制算法基于图像传感器信息计算出波前校正器控制信号。数模转换器DAC和高压放大器HVA将结果传给波前校正器形成闭环控制系统。本文以97单元变形镜作为波前校正器，97单元变形镜每个驱动器的位置排布如图2所示，各驱动器间呈正方形排布，小圆圈为驱动器符号，大圆圈为变形镜通光孔径。

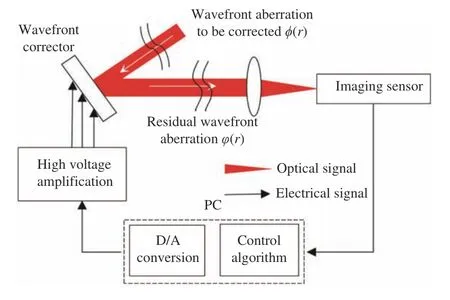
图1 无波前探测自适应光学系统Fig.1 Adaptive optical system without wavefront detection

图2 97单元变形镜驱动位置排布Fig.2 Position arrangement of 97-DM

1.2 算法原理

SPGD算法对控制参量施加正负随机扰动，采集图像数据计算性能指标变化量 ∆J。通过梯度计算控制参数，当目标函数向极大方向优化，增益系数γ取负；反之，γ取正。以迭代的方式寻找性能指标极值完成像差校正。第k次迭代时，控制参数向量u={u1,u2,···,un}的计算公式为

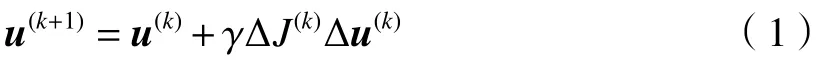
式中： ∆u(k)={∆u1,∆u2,···,∆un}(k)为第k次迭代时施加的扰动参数向量； γ∆J(k)∆u(k)为梯度估计；n为波前校正器单元数。在第k次迭代时，首先生成扰动参数 ∆u(k)， 把向量u(k)+∆u(k)加到波前校正器上，采集图像信息计算性能指标类似地把参数u(k)−∆u(k)施加到波前校正器上，采集图像信息计算性能指标然后计算再根据（1）式计算控制参数u(k+1)，重复上述过程。

2 基于FPGA的SPGD算法模块实现

为保证设计误差降到最低，首先对SPGD算法各个模块进行时序分析。利用TimeGen软件作出SPGD算法随机扰动电压的生成、性能指标的计算以及变形镜控制电压计算与输出的时序图。

2.1 随机扰动电压生成

随机扰动电压需借助多路伪随机序列生成，97路伪随机序列可由软件（如Matlab软件）产生，且需满足如下要求：N单元的变形镜需要N路伪随机序列、伪随机序列数必须是两两相互独立、满足伯努利分布。一次计数。q代表伪随机序列的数值1和0，d代表随机扰动的数值−1和1，对q设置判断条件，使q与d数值一一对应。随机扰动d与扰动幅度 α乘积产生正负随机扰动电压dv1和dv2，计数器Address和伪随机序列值q以及生成的随机扰动电压dv1和dv2的值一一对应，通过时序分析扰动幅度 α设为0.2。

将伪随机序列转化成coe文件，利用Vivado软件将coe文件存入ROM核中。FPGA 从ROM核中读取1组伪随机序列，产生正负扰动电压，时序图如图3所示。图3中Clk为时钟信号，设置计数器Address作为地址位，读取ROM核中coe文件。由于FPGA读取数据有一定的延迟，数据会在延迟2个周期后开始输出，计数器读取97次完成

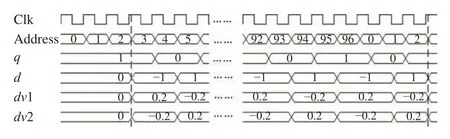
图3 随机扰动电压时序图Fig.3 Timing diagram of random disturbance voltage

FPGA不能使用小数计算，需人为计算将小数进行定点设置。扰动幅度为0.2，进行定点设置后，随机扰动电压扩大了1 024倍，转化为二进制时，二进制的低十位为小数位，精度为小数点后4位，具体值可以通过（2）式计算得到：

式中：α为实际扰动电压幅度；FPGA_α为FPGA中设 置值扰动幅度的整数。

2.2 性能指标MR计算

根据参考文献[8]，无波前探测自适应光学系统中一般选取远场光斑的平均半径MR（mean radius）作为性能指标，计算方法如（3）式：

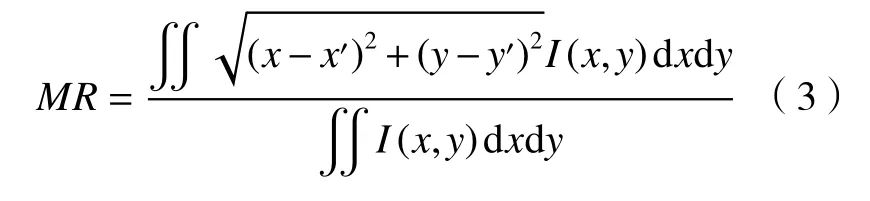
式中： (x,y) 表示光斑坐标； (x′,y′)表示质心坐标；I(x,y) 表示坐标 (x,y) 处的光强。质心 (x′,y′)计算公式为

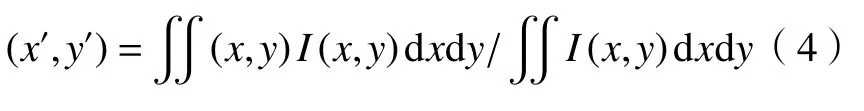
使用FPGA计算MR需要离散型数据，将质心的公式转化成：

将横坐标x与其对应光强I(x,:)乘积并累加，对所有的光强I(x,y) 求 和，得到质心横坐标x′，同理求出质心纵坐标y′，再根据（3）式求出MR。FPGA实现SPGD算法性能指标MR的计算是重要环节，具体流程图4所示。图中寄存器X_temp、Y_temp分别表示横坐标x和纵坐标y与对应光强的乘积，将矩阵元素进行相加得到远场光强SUM_q。FPGA程序无法进行除法运算，设置3个除法IP核Mr_divide1、Mr_divide2、Mr_divide3来实现质心与MR计算，Sqrt IP核用于计算。

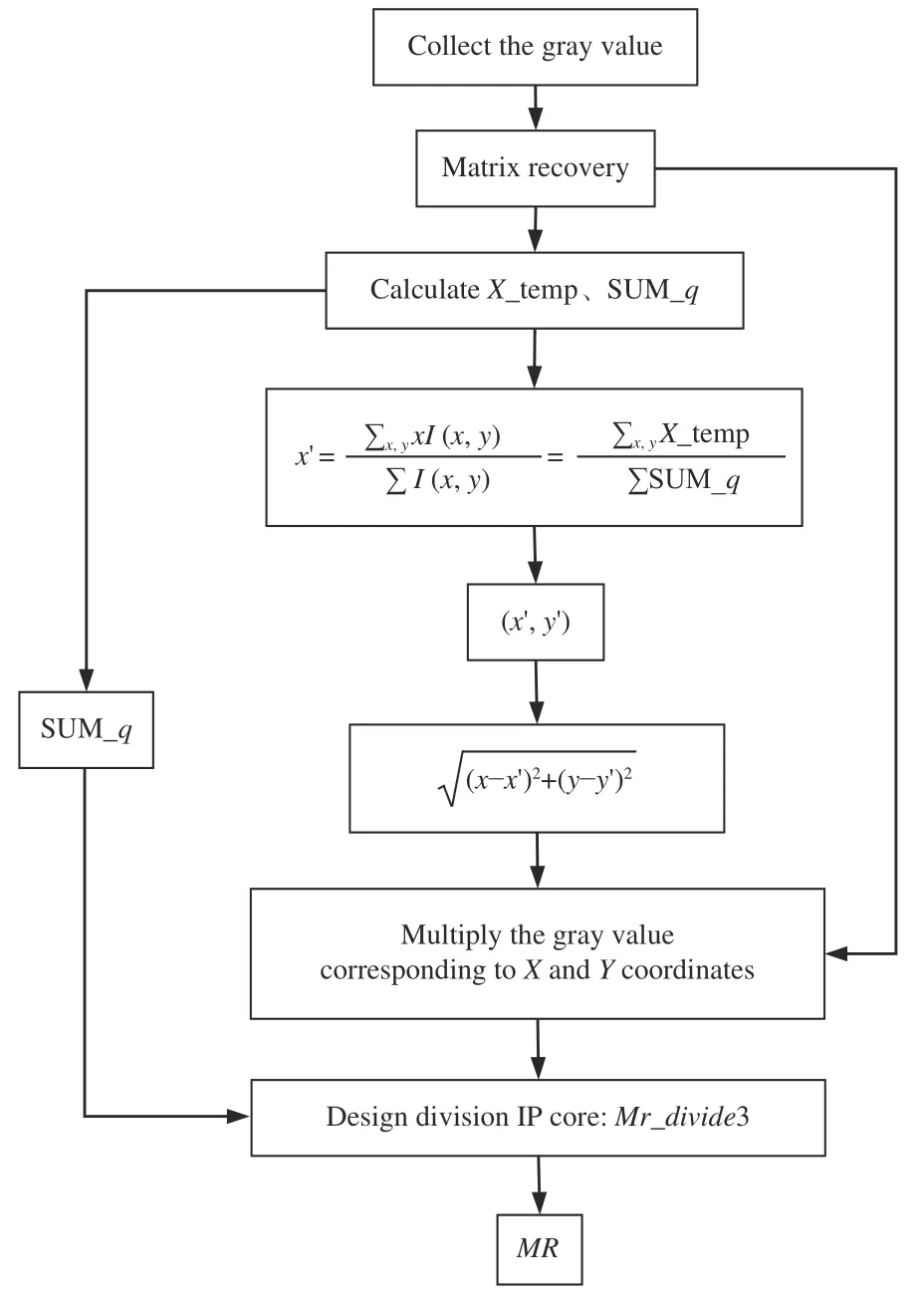
图4 FPGA实现性能指标MR流程图Fig.4 Flow chart of performance index MR implementation by FPGA

对全局时钟信号Clk进行分频得到分频信号SClk，分别作用于横坐标x和纵坐标y。在FPGA中计数器从0开始计数，设置2个计数器x_cnt、y_cnt，每到时钟Clk上升沿时，计数器y_cnt加1，当加到255时，SClk产生上升沿，计数器x_cnt加1，当x_cnt计数到255时2个计数器停止计数。由于从ROM核中读取数据存在延迟，计算得到的结果会在开始计数2个周期后输出。时序图如图5所示，FPGA读取光斑图像数据会在Address信号延迟2个周期后输出。

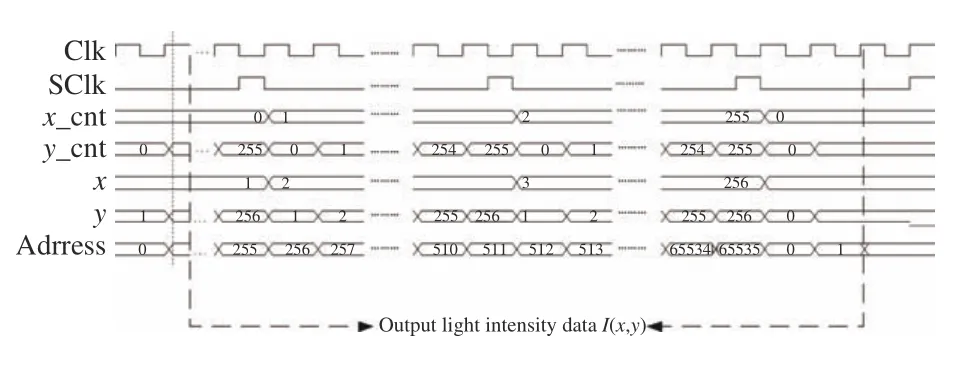
图5 性能指标MR计算时序图Fig.5 Timing diagram of performance index MR calculation

2.3 变形镜控制电压计算与输出

FPGA实现变形镜控制电压的计算分为预处理部分和计算部分，根据（1）式u(k+1)=u(k)+γ∆J(k)∆u(k)可以计算出控制电压的值，具体流程如图6所示。预处理部分为增益系数与扰动幅度的乘积，计算部分为性能指标变化量的计算。设置使能信号KZDY_done作为计算控制电压的起始信号，kzdy_d（作为随机扰动电压模块输出的d）为随机扰动电压。通过计算第k+1次正负扰动电压并将结果再传输给变形镜实现校正。根据以上分析得到变形镜控制电压的时序如图7所示。

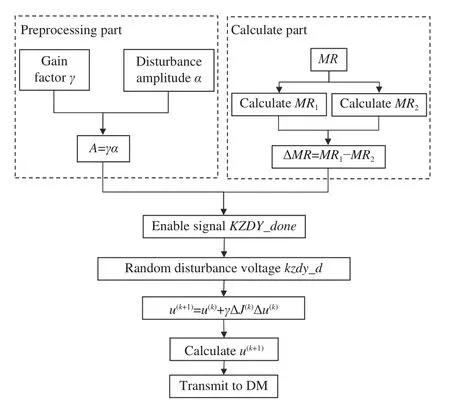
图6 变形镜控制电压流程图Fig.6 Flow chart of deformable mirror control voltage

3 结果与分析

第2节中对SPGD算法主要模块进行了时序分析，本节将各个模块的计算结果与Matlab结果进行对比，以验证本文FPGA实现SPGD算法的准确性和可行性。

3.1 随机扰动电压

将97路伪随机序列存入FPGA开发板套件的ROM核中，FPGA 从ROM中读取一组伪随机序列，生成随机扰动电压的结果如图8所示。图中q表示生成的97个伪随机数，dv1和dv2分别代表正负随机扰动电压，扰动幅度的数值FPGA_α为200，代入（2）式得到 α为0.1954。由2.1节随机扰动电压生成的时序分析，扰动幅度预设值为0.2。

图8 随机扰动电压Fig.8 Random disturbance voltage

3.2 性能指标MR

使用Matlab软件对基于97单元变形镜的SPGD算法进行分析，给系统添加湍流强度D/r0=5情况下的像差，D表示变形镜的通光孔径，r0表示大气相干长度。扰动幅度的值设为0.2，由Matlab计算的性能指标MR的值为23.0318，对应的波前相位和校正前后光斑如图9所示。

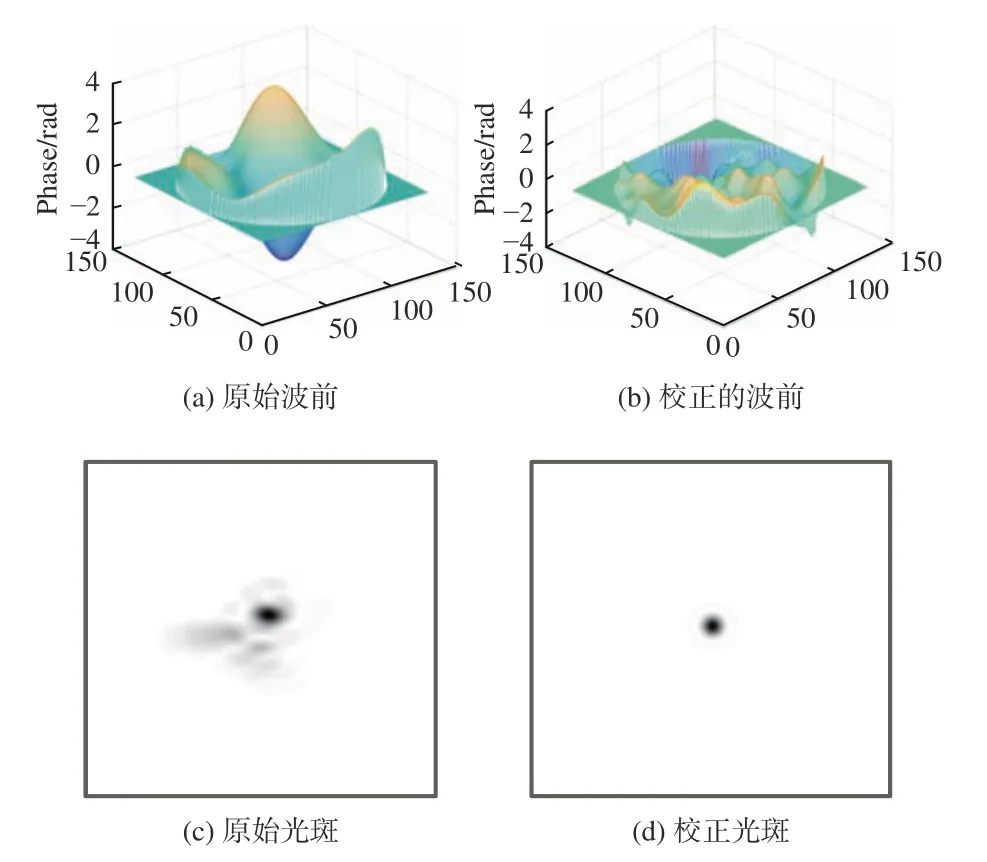
图9 D /r0=5时1帧随机波前畸变及对应的成像光斑Fig.9 One frame of random wavefront distortion and corresponding imaging spot whenD/r0=5

FPGA实现时，将湍流强度D/r0=5的像差做成coe文件存入FPGA中，借助（3）式和（5）式，以及2.2节FPGA实现MR的计算过程得到性能指标MR的值。计算结果如图10所示，将计算结果与Matlab计算结果进行对比，如表1所示。

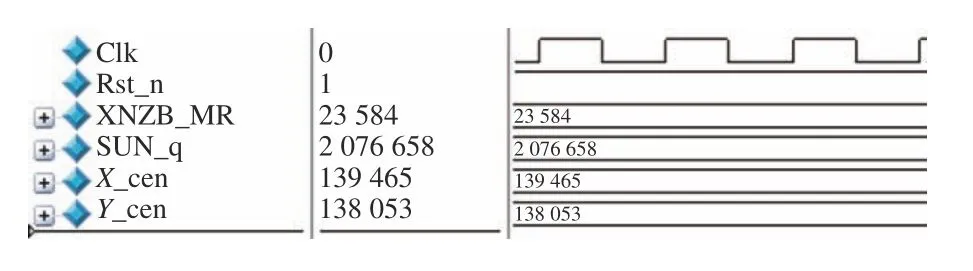
图10 性能指标计算结果Fig.10 Calculation results of performance indexes

表1 质心结果对比Table 1 Comparison of centroid results

由计算结果可以看出FPGA计算的质心坐标为（139 465，138 053），转化成小数后的实际值为（136.1963，134.8174）。性能指标MR为23 584，转化为小数后的实际值为23.0312。由表1中Matlab计算的质心坐标和性能指标数据对比，可以看出两者之间差值为0.0006，以上结果说明了由FPGA实现性能指标MR时的准确性。

3.3 变形镜控制电压

基于3.1节随机扰动电压的生成和3.2节性能指标MR的计算，设计FPGA实现变形镜控制电压的代码，结果如图11所示。FPGA结果与Matlab结果数据对比如表2所示。

表2 控制电压计算结果对比Table 2 Comparison of control voltage calculation results

图11 控制电压计算结果Fig.11 Calculation results of control voltage

由计算结果可以看出增益系数r_a的值为819，缩小1 024倍后为0.7998，与选取增益系数值0.8之间的差值为0.0002。各驱动器电压数值与Matlab计算结果相比，两者之间电压偏差值均在千分之一以内。

3.4 FPGA与Matlab计算控制电压误差分析

为保证FPGA计算控制电压的准确性，以97单元变形镜为例，在湍流强度D/r0=5的情况下，随机选取100帧像差，由Matlab和FPGA分别计算每帧像差对应的97个驱动器控制电压，并计算Matlab结果与FPGA结果的每个驱动器下100帧像差的均方根误差，如图12所示。从图中纵坐标可以看出Matlab与FPGA分别计算97单元驱动器的100帧像差的控制电压均方误差均保持在千分之一量级。

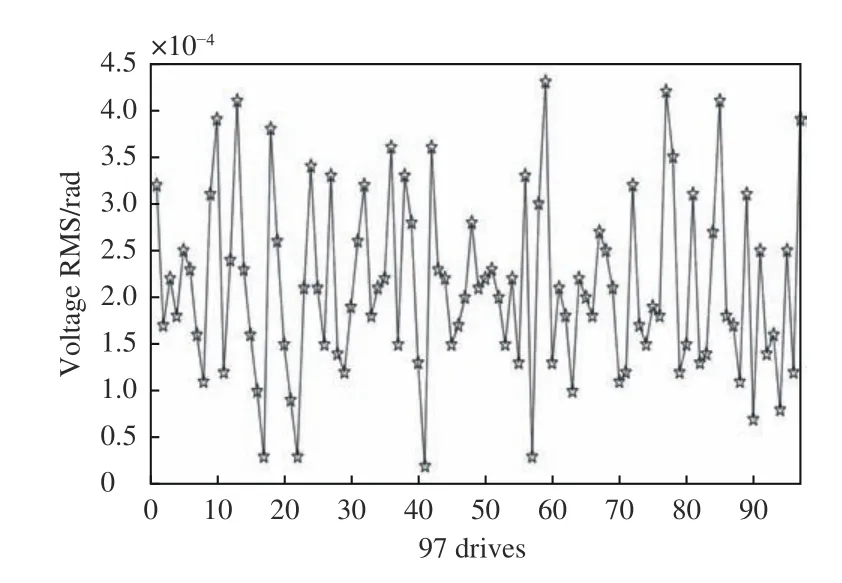
图12 97个驱动器对应的100帧像差的电压RMS值Fig.12 Voltage RMS value of 100-frame aberration corresponding to 97 drivers

根据1.1节97单元驱动器分布图，选取驱动器中心位置第49个驱动器和第69个驱动器作为测试对象，分别计算Matlab与FPGA之间的电压偏差值。图13表示第49个驱动器Matlab与FPGA计算的电压偏差值，图14表示第69个驱动器Matlab与FPGA计算的电压偏差值。从图中数据能看出第49个驱动器和第69个驱动器计算的电压偏差均保持在千分之一以内，以上数据验证了由FPGA计算控制电压的准确性。

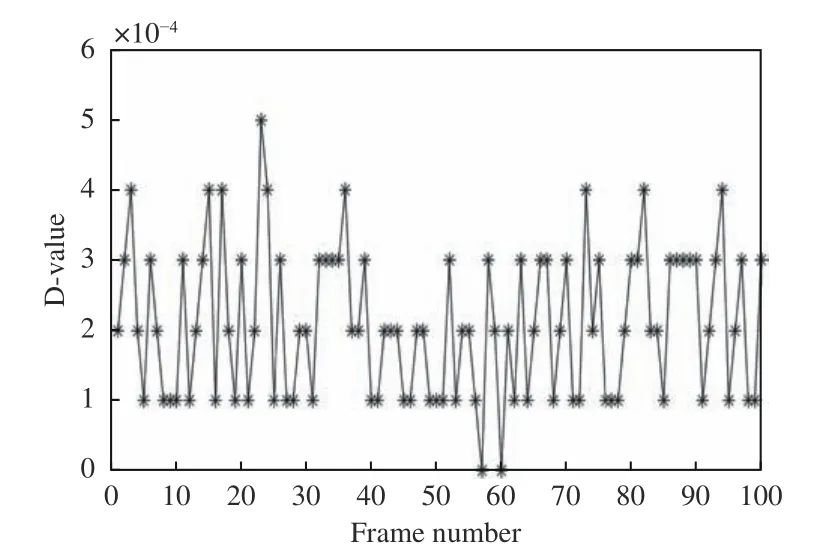
图13 第49个驱动器的100帧电压偏差值Fig.13 100-frame voltage deviation value of the 49th driver

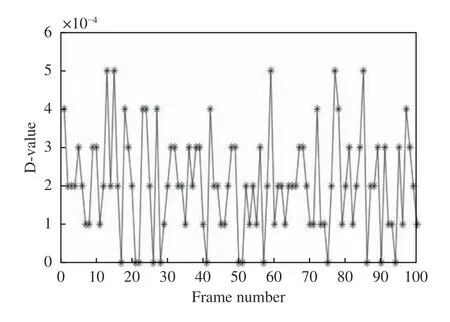
图14 第69个驱动器的100帧电压偏差值Fig.14 100-frame voltage deviation value of the 69th driver

4 结论

本文以97单元变形镜为模型，使用TimeGen软件对SPGD算法关键模块进行时序分析，再利用Vivado软件对SPGD算法关键模块进行计算，结果表明FPGA计算随机扰动幅度的值、性能指标MR以及控制电压的值与Matlab计算结果之差在千分之一以内。对100帧像差的97个驱动器控制电压进行计算，由Matlab与FPGA计算的控制电压值均方误差均保持在千分之一量级，结果验证了由FPGA实现SPGD算法的准确性和可行性，为后期基于FPGA的SPGD算法硬件实现和应用提供了基础。

在实际应用中将vivado编写的代码下载到FPGA开发板，完成FPGA版的开发和配置，从而达到FPGA直接实现SPGD控制算法的目的。FPGA的运算速度一般为ns级，解决了现有SPGD算法本身由于迭代执行而导致的自适应光学系统收敛速度慢的问题。利用FPGA实现SPGD控制算法后，自适应光学系统的收敛速度取决于成像系统采集速度和波前校正器的响应速度。基于高帧频的成像器件和响应频率在Khz以上的波前校正器，即可实现实时校正，满足应用需求。