负荷型对偶单元授权卡片交叠循环系统性能仿真
廖志华,刘建军,陈庆新,毛 宁
(广东工业大学 广东省计算机集成制造重点实验室,广东 广州 510006)
随着社会的进步和技术的发展,更具个性化和差异化的产品更能满足市场需求,企业生产模式也逐渐从传统的大批量重复制造转向以单件小批生产方式为主的非重复性制造。但该类非重复性制造系统工艺复杂多变、生产过程波动大、系统复杂度高等特点给车间内物料流控制带来了严峻的挑战。而传统的推式和拉式系统在这种环境下难以发挥作用,因此有学者提出了集中推式和拉式优点的推拉混合式系统[1],试图让其能互相弥补。
从混合方式来看,推拉混合式系统分为横向混合与纵向混合。横向混合是指在生产系统中的某一些工作站采用推式方法生产,另一些工作站采用需求拉动生产,其中较为常见的是恒定在制品(constant work-in-process,CONWIP)系统。现有对CONWIP系统的研究主要集中在其运行机制、授权卡片数量及其适用环境[2-4]。该系统的局限性在于不能对每个工作中心的负荷情况进行控制,仅仅控制了整个系统中的负荷。此外产品种类增多将导致CONWIP控制回路的激增,增加系统的复杂性。
纵向混合推拉系统以Suri[5]基于快速反应制造提出 的POLCA(paired-cell overlapping loops of cards with authorization,对偶单元授权卡片交叠循环)系统为代表,该系统上层用物料需求计划(material requirement planning,MRP)的方法确定各个任务的最早投放时间,下层用卡片拉式系统来控制,利用投放授权和限制在制品量的组合方式指导物料在车间的流转。POLCA系统具有较高的前瞻性和自我调节能力,能均衡各工作中心的队列长度,更好地适应单件小批的生产环境。现有研究主要对POLCA的系统性能进行了优化[6-9],也有部分研究针对其适应性和实用性进行了改进[10-13],文献[14]将POLCA系统与负荷控制思想结合提出一种基于负荷导向的
LB-POLCA(load-based paired-cell overlapping loops of cards with authorization)系统。LB-POLCA系统相比于POLCA系统的优势在于在工时需求差异显著时更能实现加工资源的负荷均衡,也可以避免需根据不同订单大小反复设置卡片数量这一复杂的问题。
LB-POLCA系统在工时差异显著和产品种类繁多的生产环境下具有更好的适应性和鲁棒性,但现有针对该系统的研究大多忽视了物料之间存在的装配关联性。实际生产中零件往往需要先经过机加工单元后再进入装配单元,装配工序只有在关联零件全局齐套之后才能开工。但由于零件之间工序路线和工时的差异性,产品装配关联度越大齐套越困难。此时系统控制的关键是实现关联物料的动态进度协同以满足装配物料的全局齐套需求。鉴于此,本文将LB-POLCA系统的研究扩展至带装配约束的生产环境,在此基础上给出了相适应的系统运行机制及其涉及的卡片获取规则、负荷计算方法和作业分派规则等关键控制参量,并通过大量实验揭示出不同装配关联度等级和不同系统控制参量组合下LB-POLCA的系统性能变化。
1 LB-POLCA系统运行机制
LB-POLCA将工艺路径上任意2个连续的工作中心连接起来构成一个回路,获得POLCA卡片授权意味着回路中第1个工作中心具有加工能力,同时确保回路中第2个工作中心在不久的将来对该零件有加工能力,这使得系统具有一定的远见性。每个回路的卡片只在本回路流通,卡片尺寸的大小代表了任务负荷量的大小,对回路中总的卡片数量不作限制,只限制回路中允许的负荷上界。考虑到实际操作性,此时可用电子卡片代替实体卡片。
LB-POLCA系统运行机制如图1所示。鉴于多工作中心以及多回路的表达复杂性,图中仅以零件工艺路径为A→C→D的情况为例。该零件要进入回路A-C中的A工作中心进行加工,首先需要获得一张POLCAac卡片。所以零件先进入待获卡队列Qac,触发卡片获取规则进行获卡优先级排序后,再依次遍历队列Qac中的零件,如果回路A-C的剩余可用能力大于零件对该回路的负荷贡献,则将代表了该零件负荷贡献的卡片与零件绑定。获得卡片授权之后零件和POLCAac卡片一起进入A工作中心的内部待加工队列Qa,触发作业分派规则进行上机排序。在A工作中心完成加工后,零件和绑定的POLCAac卡片一起转移到C工作中心。同理,在进入C工作中心的内部待加工队列Qc之前,要先在待获卡队列Qcd处获取一张POLCAcd卡片。换言之,在C工作中心,该零件同时具有两张POLCA卡片,一张POLCAac卡和一张POLCAcd卡。一旦在C的加工完成,当且仅当此时,POLCAac卡片与零件解绑并释放回回路AC以供其他零件继续进行获卡操作。如后面还有回路存在,则按照上述规则继续进入下一个工作中心。如果后面不存在其他回路,例如本例中D为最后一个工作中心,零件在C工作中心加工完成之后可直接进入D工作中心的待加工队列Qd等待上机加工,无需再获取POLCA卡片。在最后一个工作中心加工完成之后,卡片与零件解绑,POLCAcd卡片释放回回路C-D,加工完成的零件进入装配区等待齐套装配。
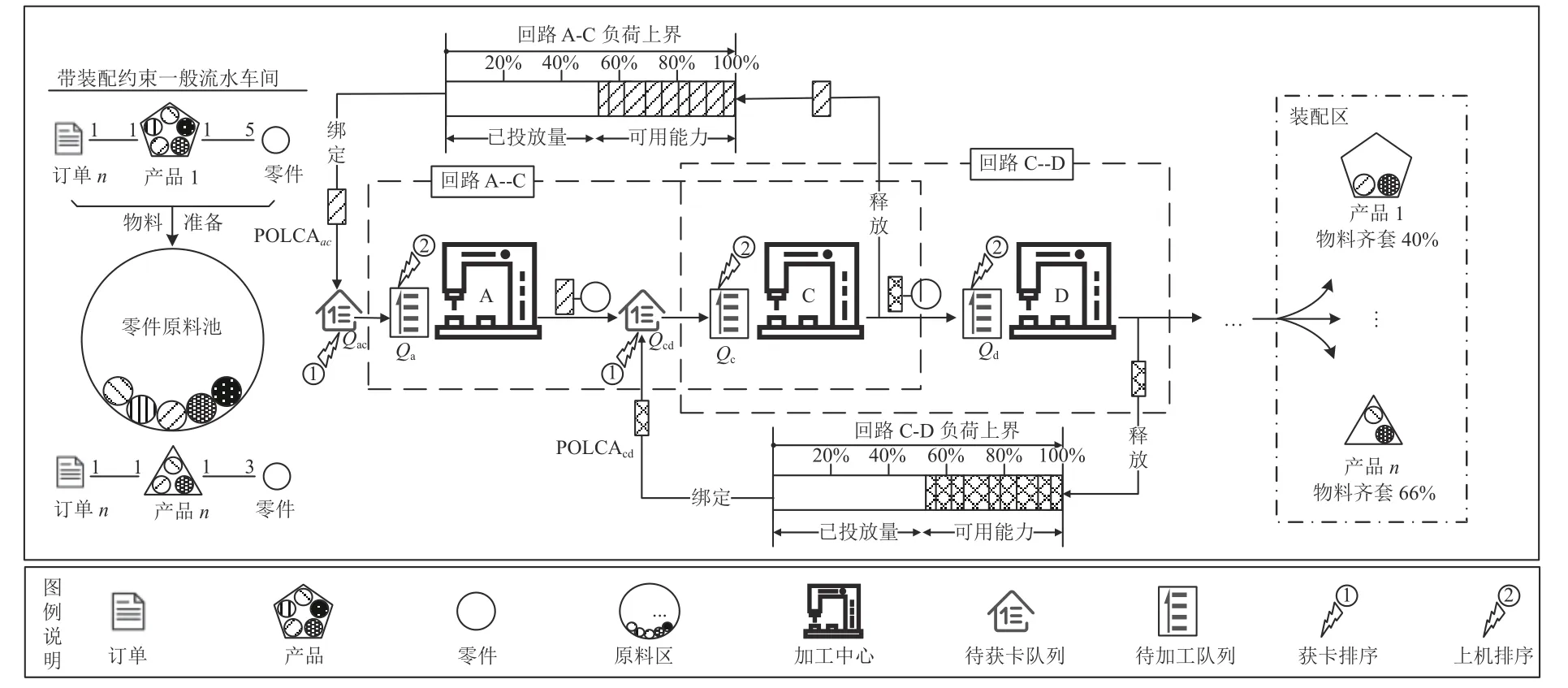
图1 LB-POLCA系统运行机制Figure 1 Operation mechanism of LB-POLCA system
2 系统控制参量
卡片获取规则和作业分派规则是LB-POLCA系统里原有的两个控制参量,传统使用的都是基于MRP的最早投放时间优先(earliest release date,ERD)规则,且必须要达到任务的最早发布时间,才能授权机器开始加工。但是文献[15]指出这将具有短视性,因此在本文中无论是否已达到该任务的最早发布时间,都可授权机器开始加工。LB-POLCA系统用回路之间的负荷上界替代了回路中允许流通的POLCA卡片数量,减少了卡片数量这一控制参量,但同时也引入了两个新的控制参量:回路的负荷上界、POLCA卡片所应代表的负荷量。为探究不同系统控制参量组合在装配约束环境下对系统性能变化的影响,以下将分别给出其相适应的卡片获取规则、负荷计算方法和作业分派规则。
2.1 卡片获取规则
卡片获取规则的作用是确定未绑卡零件获得POLCA卡片的优先级,目的是将合适的任务投放或转运至工作中心,构建合理的上机加工任务集合。本文所研究的是具有装配约束关系的车间生产环境,在任务投放和转运过程中需要考虑同属订单各任务彼此间的生产进度协同,因此本文考虑了基于静态协同、动态协同及负荷均衡3种不同规则导向的代表性规则。
1) 最早投放时间优先(ERD)。ERD规则是在LBPOLCA系统中典型使用的规则,根据任务的最早投放时间进行优先级排序。任务的最早投放时间根据静态向后倒排方法计算。该规则为静态协同规则,其优先度Zij可表达为

其中,trij为订单i零件j的投放时间。
2) 重要程度-总剩余工作量优先(importance ratiototal work remaining,IR-TWKR)。关联零件中剩余工序数量最多的零件为关键件,其将制约着装配工序的开工,应该优先加工。IR值为各零件剩余工序数量与关键件剩余工序数量的比值,IR值越大,优先度越高。如果IR值相同,则使用TWKR规则再次进行排序。该规则为动态协同规则,其优先度Ζij可表达为

其中,Ji为订单i的零件数目;NUOij为订单i零件j的剩余工序数量。
3) 产能松弛量优先(capacity slack,CS)。该规则从负荷均衡角度来考虑优先级,以零件的产能松弛率进行排序,产能松弛率越小,具有的卡片获取优先级越高。其优先度Zij的计算表达式为

该规则考虑了3种影响因素:1) 零件对工作中心s的负荷贡献Lsij,其中s∈Rij,Rij为订单i零件j的未加工工序所对应的工作中心集合;2) 工作中心负荷上界与现有负荷量之间的负荷差距Ns-Ws;3) 剩余工艺路径长度nij。由于在LB-POLCA系统中负荷上界存在于两个工作中心之间的回路中,并不直接代表工作中心的负荷上界,因此本文将工作中心所涉及到的每一个回路的负荷上界相加,再除以回路中的工作中心数量,以此作为每个工作中心的负荷上界Ns。而且LB-POLCA系统机制并没有限制工作中心的负荷量Ws,因此在计算优先级时可能会出现Ws大于Ns的情况,导致产能松弛率变为负数,使得会加剧工作中心超负荷情况的零件反而具有最高获卡优先级。为避免出现这种情况,当Ns-Ws≤0时,用一个无穷大数M代替1/(Ns-Ws),在此次排序中将该零件移至待获卡零件队列的队尾。
2.2 负荷计算方法
在传统POLCA系统中,一张卡片代表一个任务,主要的问题在于确定卡片的数量。而在LBPOLCA系统中,不需确定卡片的数量,这里的关键问题是如何为绑定在零件上的POLCA卡片估算合理的负荷大小。在负荷控制理论中,对负荷的估算方法可归为3类。第1类是直接负荷,将任务对工作中心产生的直接负荷作为负荷贡献[16]。第2类是综合负荷,将上游任务对工作中心的直接负荷和间接负荷相加,以此作为任务的负荷贡献[17]。第3类是修正综合负荷,将上游任务对工作中心所产生的负荷贡献,根据工序所在工艺路径的位置作一个相应的折算[18],该方法在负荷控制(work-load control,WLC)理论中被认为作用显著。基于上述负荷控制理论,本文考虑了4种POLCA卡片负荷的计算方式。
1) 以回路中第1道工序的加工负荷作为POLCA卡片代表的负荷,即只考虑直接负荷。第1类负荷计算方法(1st)为

2) 以回路中第2道工序的加工负荷作为POLCA卡片代表的负荷。即只考虑间接负荷。第2类负荷计算方法(2nd)为

3) 以回路中第1道工序和第2道工序的总负荷作为POLCA卡片代表的负荷。将直接负荷和间接负荷相加综合进行考虑。总负荷计算方法(agg)为

4) 以回路中第1道工序的直接负荷和第2道工序的折算负荷之和作为POLCA卡片代表的负荷。同样综合了考虑直接负荷和间接负荷,不过对间接负荷进行了相应折算。折算负荷计算方法(cor)为

2.3 作业分派规则
前述卡片获取规则的目的是将合适的任务投放或转运到工作中心,而作业分派规则的目标是确定工作中心上任务的合理加工顺序。为分析作业分派规则的分派能力强弱影响,文本选取了先到先服务(first come first served,FCFS)、ERD及修正工序交期(modified operation due date,MODD) 3种不同分派能力的规则。MODD规则综合考虑了零件的工序交期和工序最快完成时间,优先值Kij由式(8)确定,Kij值越小,零件加工优先级越高。

其中,tdijk为订单i零件j工序k的工序交期;t为当前决策时刻;pijk为订单i零件j工序k的加工工时。
3 仿真实验
3.1 仿真模型设定
单件小批生产通常采用功能形布局的车间形式组织生产。但在实际生产中以纯流水或纯作业形式进行生产过程组织却并不多见,更多的是采用具有主定向工艺路径的一般流水车间[19]。考虑到现实产品需要经过零件加工和产品装配两个阶段,所以本文以带装配约束的一般流水车间作为仿真研究对象。同时为了确保所得结论的普适性,文中所构建的模型具有通用性,实验数据采用分布函数进行随机生成。
仿真模型工作流程分为2个阶段,如图2所示。第1阶段是加工阶段,车间由6个不同的工作中心构成,每个工作中心的加工能力恒定,各工作中心被采用的概率均等(不存在固定瓶颈工序),且在每个零件的加工路径中某个工作中心最多被采用一次。第2阶段是装配阶段,零件加工完成之后进入装配车间等待装配,装配过程采用完全齐套装配方式,并假定装配工序的能力充足,装配所需时间稳定。
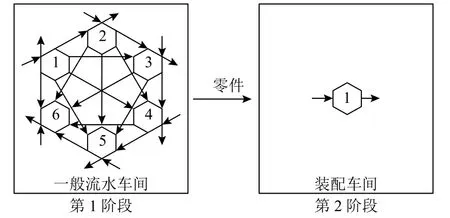
图2 具有装配约束的一般流水车间模型Figure 2 General flow shop model with assembly constraints
生产订单i随机到达,到达时间服从指数分布,每个订单仅包含1套产品生产需求,由j个零件组装而成,零件数量服从均匀分布。各零件的工序数服从[2,6]的离散均匀分布,零件工艺路径随机但具有主流向。各工序的加工工时服从均值µ=1,峰值max=4的二阶截尾爱尔朗分布,加工准备时间包括在加工时间内。假设新到达订单i的承诺交货期在到达订单池时已知,且tdi=tai+Ti;其中tdi为订单i的承诺交货期,tai为订单i到达订单池的时刻,Ti为服从[60,85]的均匀分布。仿真模型的设定总结于表1中。
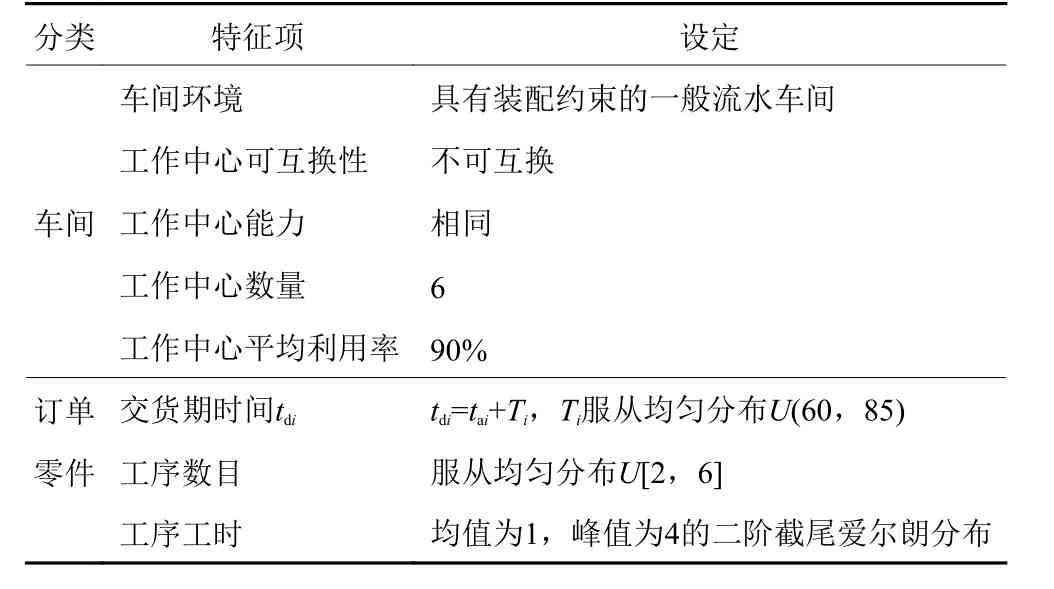
表1 仿真模型参数设定Table 1 Parameter setting of simulation model
本文考虑的是适合于LB_POLCA系统的单件小批量生产环境,而单件小批生产一般具有以下特点。1) 面向订单生产。定制型企业业务需求不稳定,订单的到来具有随机性,在计划期内企业可以接到的订单数量、客户订单的具体要求等都无法事先确切知道,需按客户订货要求组织生产。2) 生产过程多变。单件小批生产的稳定性和专业化程度较低,加工工时不确定,生产中所用设备多为应变能力较强的适合于多品种生产的通用设备。3) 生产的产品少量多样。单件小批生产产品品种多,每种产品的生产数量少,且产品各零部件之间的成套性要求严格。所以本文设置了此类具有高度订单到达时间可变性、加工时间可变性、工艺路径可变性、产品BOM结构可变性的随机性仿真环境以期满足单件小批量具有随机性需求的动态生产环境要求。
3.2 车间性能指标
如表2,本文将流水时间类与交货期类两类指标作为车间性能评价指标。流水时间类指标中零件平均车间流水时间,代表了车间的在制品(work-inprocess,WIP)水平,订单平均提前期指标能从订单层面评价订单从到达到完成的通过时间。在按单生产的生产模式下,订单拖期率与订单拖期量体现了企业的履约能力。对于合同违约惩罚和失去客户信誉费用成本较高的企业来说,更高的订单按时交付率是保障企业能良好运作的基础。此外,车间生产仿真时间长度为1 300 d (大于40 000个零件被加工),为了避免仿真前期阶段系统初始条件所带来的影响,将前300 d时间作为仿真预热时间,各指标数据将在预热时间后统计。
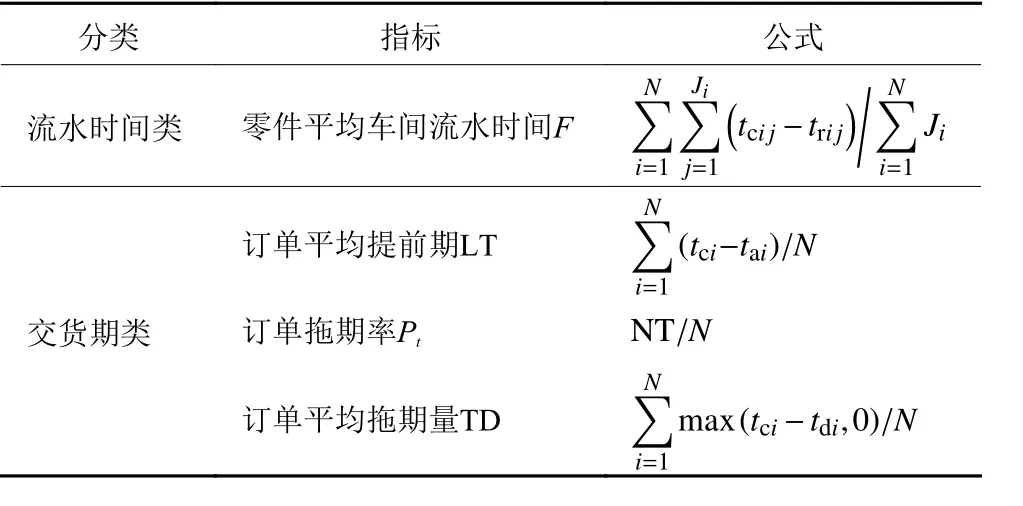
表2 车间性能评价指标Table 2 Performance measures of workshop production
表2中,tcij为订单i零件j的完工时间;trij订单i零件j的投放时间;N为完工订单的数量;Ji为订单i包含的零件数;tci为订单i的完工时间;tai为订单i的到达时间;NT为完工订单中的拖期订单数量;tdi为订单i的交货期时间。
3.3 实验设计
为探究LB-POLCA在不同装配关联度等级和不同系统控制参量组合下的系统性能变化。实验设定了Ⅰ、Ⅱ、Ⅲ、Ⅳ(以下分别称为无装配关联、装配关联度低、装配关联度中、装配关联度高)4种装配关联度等级的订单环境,每种等级下订单包含的零件数j分别服从[1,1]、[1,4]、[2,6]、[3,8]的离散均匀分布,订单到达间隔时间分别服从均值为µ=0.721,1.817,2.941,4.077的指数分布,以便车间利用率都为90%。装配关联度等级设置总结见表3,并设置了多个负荷上界取值以体现不同负荷上界的取值对车间性能的影响。考虑到不同的负荷计算方式涉及到的工作中心数目不一样,参考文献[20]并基于预仿真实验,在第1类和第2类负荷计算方式中回路负荷上界分别设置为12 h、14 h、16 h、18 h、20 h、22 h及无限负荷;在总负荷计算方式中回路负荷上界分别设置为24 h、28 h、32 h、36 h、40 h、44 h及无限负荷;在折算负荷计算方式中回路负荷上界分别设置为18 h、22 h、26 h、30 h、34 h、38 h及无限负荷。每次实验中各个回路负荷上界相等。实验在卡片获取层选取了面向静态进度协同的ERD规则、面向负荷均衡的CS规则、面向动态进度协同的IR规则(用TWKR打破平衡)。在底层作业分派层选择了FCFS、ERD、MODD 3种不同分派能力的作业分派规则。实验影响因子有5类,分别为:1) 装配关联度等级;2) 卡片获取规则;3) 负荷计算方法;4) 回路负荷上界;5) 作业分派规则。实验因素及其水平总结见表4。对实验因素各水平设置进行全因素正交实验,共4×3×4×7×3=1 008组实验,各实验组进行90次重复实验。

表3 装配关联度等级设置Table 3 Setting of assembly correlation level

表4 实验因素及其水平Table 4 Experiment fators and levels of experiment
4 实验结果分析
本节将分析作业分派规则为FCFS时LB-POLCA系统在4种产品装配关联度等级下的适应性以及卡片获取规则、负荷计算方式两个控制参数对车间性能的影响,并将这作为比较基准,在改变作业分派规则的基础上评估作业分派规则的影响及之前结论的鲁棒性。
实验结果如图3~5所示。为了更好地对比卡片获取规则与负荷计算方式不同组合间的差异,图中每条曲线均表示了卡片获取规则和负荷计算方式两个维度,采用了不同线形和符号的成组图例来区分表达。如图例“ERD &1st”表示卡片获取规则为ERD,负荷计算方式为第1类负荷计算方式。图中每一个数据点表示一种回路负荷上界,从左往右负荷上界依次递增。即最左边的点表示回路负荷上界最小的情况,最右边的点表示负荷上界无穷大的情况,意味着此时任务直接投放,不受LB-POLCA投放授权的限制,所以所有曲线在最右边都集中于一点。
图3展示了在FCFS作业分派规则下4种装配关联度等级的订单平均拖期率、订单平均提前期、订单平均拖期量关于零件车间平均流水时间的变化。因为不同分派规则的影响将在4.4节讨论,所以图3只展示了在FCFS作业分派规则下的情况。
4.1 LB-POLCA总体适应性分析
对比图3(a)~(d)可知,在有装配约束和无装配约束的情况下,相比于直接投放,LB-POLCA系统均能有效降低零件平均车间流水时间。这是因为回路的负荷上界限制了车间的在制品数量,使得零件通过车间的速度加快。同时订单拖期率指标也能得到有效的降低(图3(a1)~(d1)),这是由于LB-POLCA稳定了各工作中心的加工负荷,增强了零件的完工可预见性,虽然也以牺牲了一定的订单拖期量为代价。
可是,LB-POLCA系统在装配约束环境下也表现出了一定的局限性。如无装配约束时,LB-POLCA系统能缩短订单提前期(图3(a2)),而在有装配约束环境下非但不能缩短订单提前期,且随着装配关联度的提高,订单提前期相对延长的也越多(图3(b2)~(d2))。这可能是因为装配产品需要满足齐套装配,而LB-POLCA制约了产品中某些任务不能及时获取到POLCA卡片进入工作中心进行生产,装配关联度越高,被制约的概率越大,导致某些任务拖累了整个产品的完成。
4.2 卡片获取规则影响分析
由图3可以发现,在无装配约束情况下,对于拖期量而言,存在ERD略好于CS和IR的情形(图3(a3))。而在有装配约束情况下,装配关联度较低时,对于同一负荷计算方式,面向负荷均衡的CS规则和面向动态协同的IR规则在拖期率方面显著优于面向静态协同的ERD规则,在拖期量和提前期方面也略优于ERD规则。且随着装配关联度的提高,对于拖期量和提前期指标,3种卡片获取规则之间的相对变化没有表现出太大的差异,但是对于拖期率指标,CS和IR规则却比ERD规则表现得越来越好(如图3(b1~d1))。这是因为CS规则可以将仅含有中小工时的订单按时投放以促进生产的流动性,而把含有大工时的任务推后(工况闲时)投放。而IR规则可以提高订单中关键零件的投放优先度,减少关键零件的投放等待时间。说明在全局齐套装配需求下,负荷均衡类和动态进度协同类的卡片获取规则比LB-POLCA原有的ERD规则更能发挥效力。
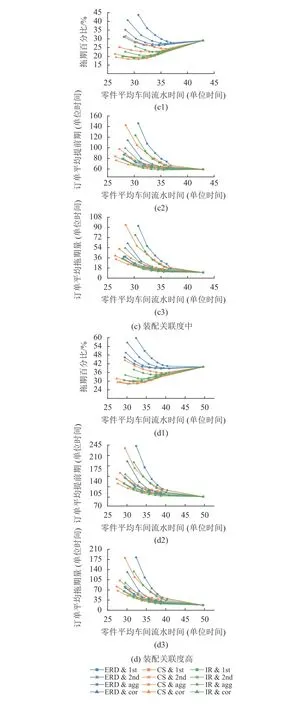
图3 作业分派规则为FCFS时,4种装配关联度下的各项指标性能Figure 3 Performance results for FCFS dispatching in combination with the four levels of assembly relevancet
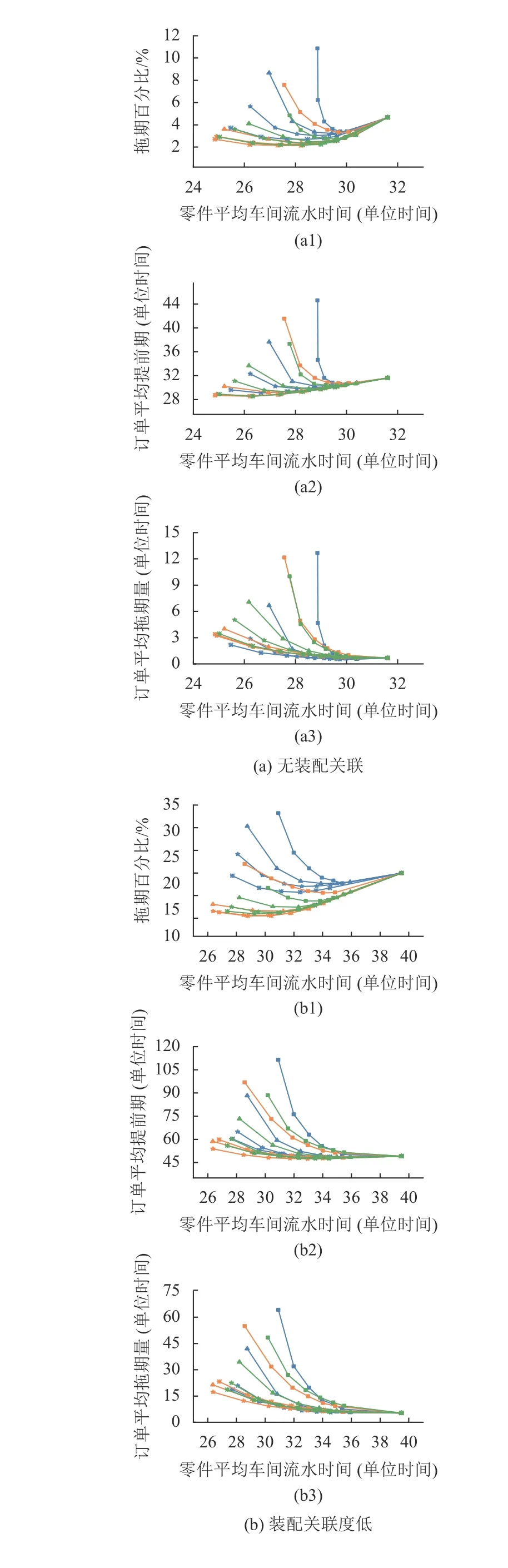
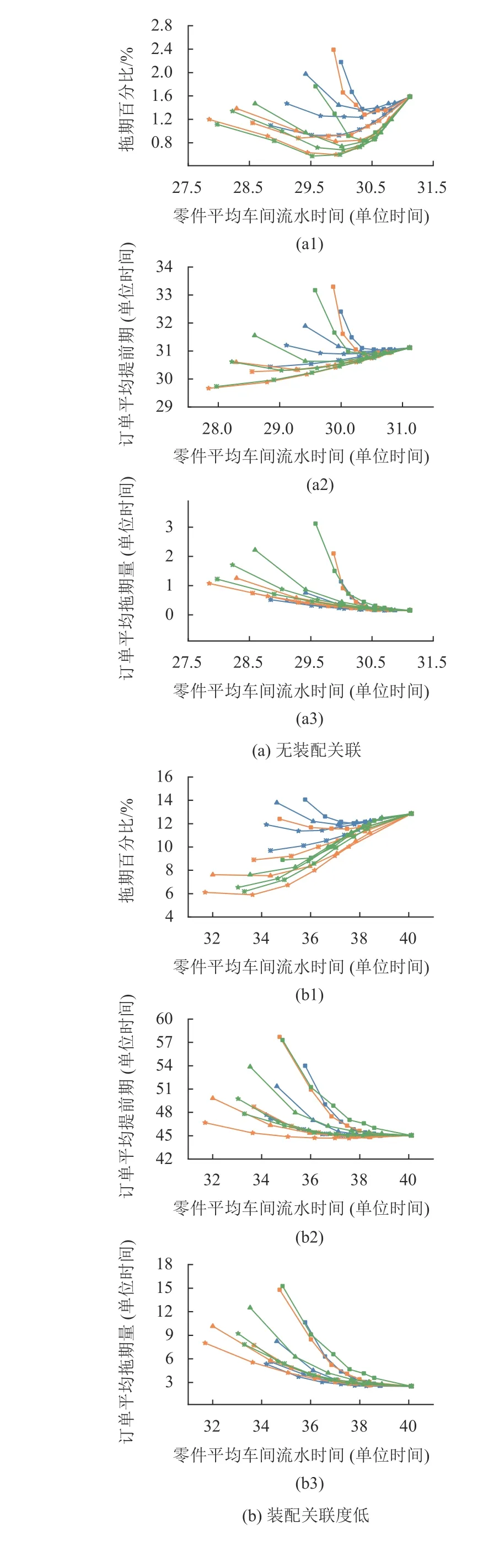
在同等装配关联度等级下,对于同一负荷计算方式,不同卡片获取规则之间的性能差异随着负荷上界的降低而逐渐增大。这是因为随着回路负荷上界的降低,待获卡队列长度增加,强化了卡片获取规则的选择效力,而较低的车间在制品水平削弱了作业分派规则的影响。
4.3 负荷计算方式影响分析
对于同一指标,4种负荷计算方式在不同的卡片获取规则下表现各异,但也有一定的规律可循。
1) 对于订单提前期和订单拖期量这两类指标,负荷计算方式在ERD、IR这2种进度协同类规则下表现得类似。在没有装配约束时,以第2类负荷折算方式较好(图3(a2)和(a3)),但随着装配关联度的增加,第2类负荷折算方式的优势会逐渐衰退,进而被总负荷计算方式替代(图3(d2)和(d3))。
2) 对于订单拖期率,随着装配关联度的增加,在IR规则下最优负荷计算方式从第2类负荷计算方式转变为总负荷计算方式。在ERD规则下虽然第2类负荷折算方式一直表现最优,但也有被总负荷计算方式替代的趋势。而对于CS规则,3类指标一直是以总负荷计算方式最优。这可能是因为在CS规则下,以总负荷计算方式作为卡片负荷计算方式时,零件的卡片获取难度较小,更加有利于重要零件获得卡片授权进行加工。
其次在相同装配关联度下对于同一种卡片获取规则而言,第1类负荷计算方式的表现都最差,因为第1类负荷计算方式具有短视性,仅考虑了当前即将要进行加工的工作中心的负荷情况;另外总负荷计算方式都要优于折算负荷计算方式,但是折算负荷计算方式在负荷控制理论领域却被证实有显著作用,近年来也一直被学者所采用[21]。这表明负荷控制理论中常用的负荷计算方法难以直接应用于LB-POLCA系统中。
4.4 作业分派规则影响分析
图4(a)~(d)分别展示了在ERD作业分派规则下4种装配关联度等级的订单平均拖期率、订单平均提前期、订单平均拖期量关于零件车间平均流水时间的变化。图5(a)~(d)分别展示了在MODD作业分派规则下4种装配关联度等级的订单平均拖期率、订单平均提前期、订单平均拖期量关于零件车间平均流水时间的变化。
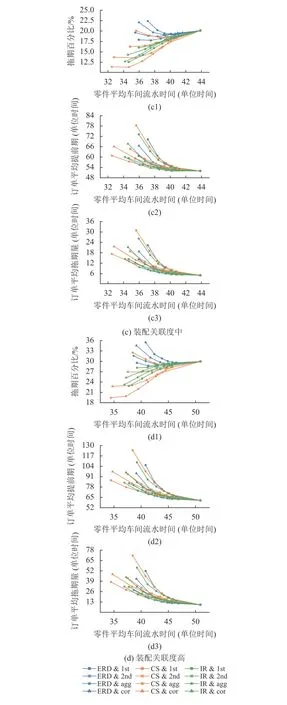
图4 作业分派规则为ERD时,4种装配关联度下的各项指标性能Figure 4 Performance results for ERD dispatching in combination with the four levels of assembly relevancet
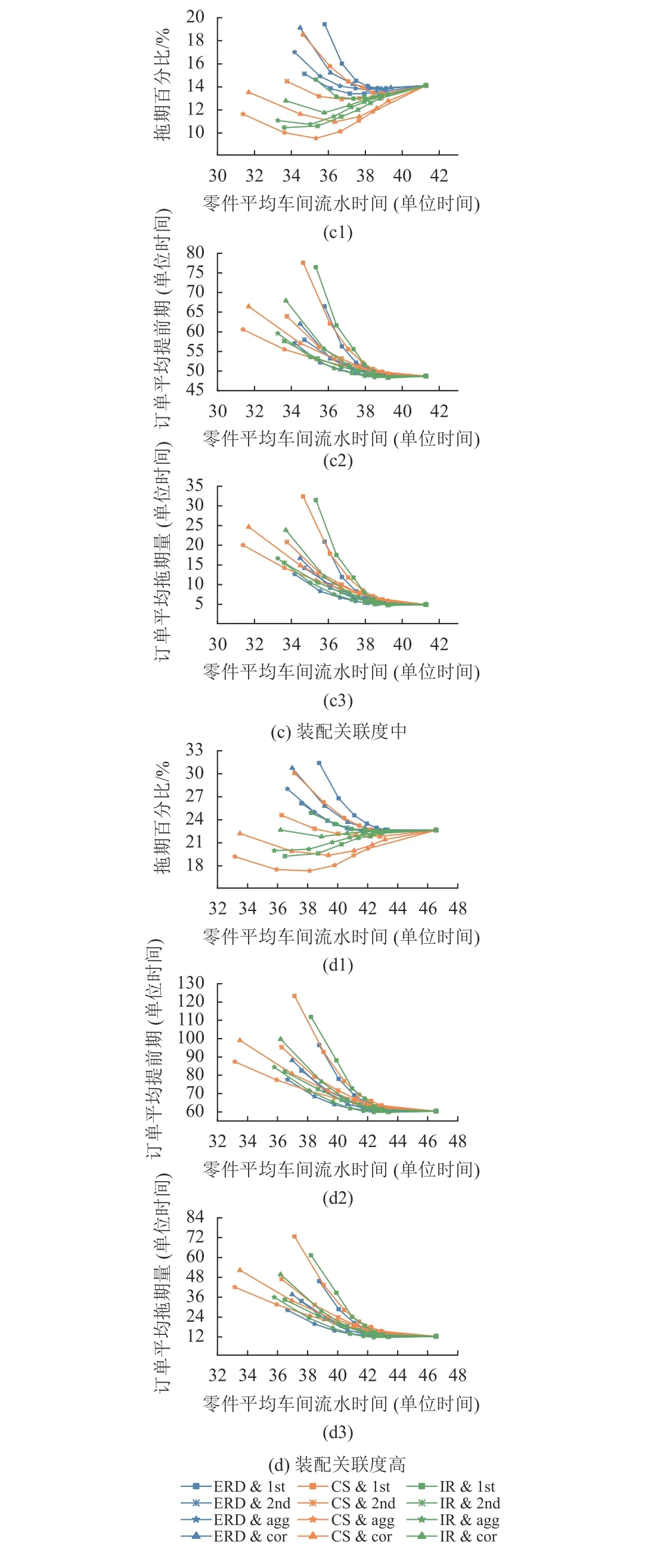
图5 作业分派规则为MODD时,4种装配关联度下的各项指标性能Figure 5 Performance results for MODD dispatching in combination with the four levels of assembly relevancet
分别对比图3~5的(a)、(b)、(c)、(d) 中同一类指标(如对比图3(d1)、图4(d1)、图5(d1)),从指标最右边点的具体数值来看,即在只受到分派规则的影响下,3种分派规则性能表现的优秀程度从低到高依次是FCFS、ERD、MODD。这是因为MODD融合了最短加工时间(shortest processing time,SPT)和工序交期(operation due date,ODD)的影响因素,既考虑了零件完工准时性,在存在多个紧急零件竞争加工资源时又能让工时较短的紧急零件尽快完工,加速其尽快通过车间,而ERD仅考虑了零件的准时性。这也从侧面验证了之前实验设计关于FCFS、ERD、MODD3种作业分派规则具有不同分派能力的正确性。
从图4和图5可以看到,当作业分派规则为ERD和MODD时,在不同装配关联度下对应指标的变化规律与作业分派规则为FCFS时的变化规律相似,图像曲线之间的相对变化也较小。在ERD、MODD分派规则下的所得结论大部分与4.1~4.3节在FCFS分派规则下所得结论相同。但是也有一些不同之处,主要体现以下2个方面。1) 作业分派规则能力变强时,在紧负荷上界下,CS和IR卡片获取规则的零件车间流水时间较ERD规则明显缩短。2) IR规则在分别结合ERD和MODD这两种作业分派规则时,拖期率一直以第2类负荷计算方式为最优,其次是总负荷计算方式,但这两种负荷计算方式之间的差距随着装配关联度的增加也持续在缩小。
虽然图像总体趋势相同,但在同一装配关联度等级下从3种指标具体数值来看,可以发现作业分派规则的能力越强,对系统整体性能提升得越大,但性能提升的幅度也受卡片获取规则能力的影响。与表现较好的卡片获取规则(CS)结合时性能提升的幅度要小于与表现较差的卡片获取规则(ERD)结合时提升的幅度。而从整个实验来看,CS、IR卡片获取规则与MODD作业分派规则结合时的整体性能表现要强于其他规则组合,即此时能在最大限度降低拖期率的同时,将对订单提前期和订单拖期量的损害维持在相对较低的水平。说明卡片获取规则和作业分派规则的耦合性能要优于两者单独的性能,两者能起到相互促进的作用,可以通过设置更优的规则组合来使LB-POLCA系统获得更好的性能增益。
5 结束语
LB-POLCA是一类面向非重复性制造车间的新型物料控制系统,能有效促进工作中心之间的信息反馈与负荷均衡。在没有过多增加在制品库存的基础上,保持生产所需物料在车间的流动性。然而现有针对该系统的研究大多忽视了物料之间存在的装配关联性。基于此,本文利用Plant Simulation仿真平台进行了大量实验,以探索LB-POLCA在不同装配关联度等级和不同系统控制参量组合下的系统性能变化。仿真结果表明:1) 在考虑装配约束时,LBPOLCA既有有效性也有局限性,有效性体现在可有效降低订单拖期率和缩短零件车间流水时间,局限性体现在会导致订单提前期延长;2) 在全局齐套装配需求下,动态进度协同类和负荷均衡类的卡片获取规则比LB-POLCA传统的ERD规则更能发挥效力;3) 以总负荷计算方式和第2类负荷计算方式作为对POLCA卡片负荷量的估算方式效果更好,且随着装配关联度的增加,总负荷计算方式有占据更多优势的趋势;4) 卡片获取规则和作业分派规则的耦合性能要优于两者单独的性能,两者能起到相互促进的作用。
针对研究的不足,未来可从以下方面进行研究:1) 进一步对LB-POLCA的机制进行优化,使之降低在装配环境下的局限性;2) 进一步扩展研究对象,结合更现实化更复杂化的实际生产过程进行研究;3) 考虑紧急插单、工件返修、机器故障等干扰因素,探索LB-POLCA对于此类扰动情形的抗干扰能力。

