基于Lévy Flight的混合GA在柔性作业车间调度问题中的性能分析
张正敏,管在林,岳 磊
(1.华中科技大学 机械科学与工程学院,湖北 武汉 430074;2.广州大学 机械与电气工程学院,广东 广州 510006)
柔性作业车间调度问题(flexible job-shop scheduling problem, FJSP)是目前制造业中常见的简化生产模型,FJSP问题已被证明为NP难问题[1],计算复杂度及时间开销随着问题规模的增大呈指数增长,故使用精确算法较难快速解决问题。相比之下,元启发式算法基于其简单的算法结构与高效的迭代机制,被广泛用于各类生产组合优化问题。常用的元启发式算法包括遗传算法(GA)、模拟退火算法(SA)、人工蜂群算法(ABC)、禁忌搜索算法(TS)等,不同的算法在鲁棒性、全局/局部搜索能力等特征上具有不同的表现,因此不少学者将不同元启发式算法进行混合,形成各类混合式启发算法,以期望提高其综合搜索能力。由于综合了各自算法的搜索优点,部分混合算法在调度问题上取得了较好的结果。Karimi等[2]提出了一种新的混合模拟退火的帝国主义竞争算法求解考虑运输时间的柔性作业车间调度问题。Jolai[3]提出了一种新的混合启发式算法,用于求解具有顺序相关的安装时间的无等待柔性流水车间调度问题。赵诗奎[4]针对柔性作业车间调度问题,以最小化最大完成时间为求解目标,提出了一种混合双层邻域搜索和遗传算法的混合算法。Wang等[5]提出了一种混合人工蜂群算法求解模糊柔性作业车间调度问题并证明了算法的高效性。
遗传算法(GA)框架稳定,全局优化能力强,故不少学者使用GA进行求解组合优化问题。然而,GA的局部搜索能力较弱,因此部分学者将局部搜索能力较强的算法与GA混合,形成混合GA求解问题[6-12]。Costa等[6]提出了一种融合遗传算法和随机抽样搜索方法特征的混合启发式算法,用于解决序列相关的流程车间成组调度问题。Gu[7]提出了一种基于自适应遗传算法和改进蚁群算法相结合的作业车间调度混合优化算法并通过实验证明该算法针对大规模问题具有更好的效果。Shahsavari等[8]在遗传算法框架的基础上,结合模拟退火算法的思想形成了新的混合遗传算法,用于求解FJSP问题。Ren等[9]提出了一种混合遗传算法求解作业车间调度问题。为了增加种群的多样性,该混合算法中使用了一种基于适应度值和浓度值的混合选择算子。
本文提出了一种基于Lévy flight的混合GA算法。Lévy flight是自然界中很多鸟类遵从的一种飞行方式[13]。Lévy flight作为一种随机游走方式,其短跳跃的搜索方式与偶尔长跳跃的搜索方式交叉执行,如图1所示。Lévy flight保证了算法能够及时跳出局部最优点,扩大了粒子的搜索范围,增加了个体多样性并增强了算法搜索能力。
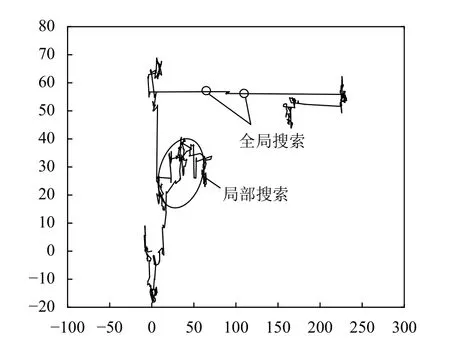
图1 连续Lévy flight搜索过程Figure 1 The search process of continuous Lévy flight
借助Lévy flight策略,Yang等[13]提出了布谷鸟算法(CS),CS最先用于解决连续优化问题,并被证实取得了较好的效果。本文在GA框架的基础上,研究了一种新的离散化Lévy flight策略对种群进行局部优化,进一步利用Lévy-GA算法求解FJSP,并通过对比TLBO[14]、CS、GA等算法求解,结果证明Lévy flight用在GA等全局优化性能较强的算法中时具有更好的效果。
1 问题描述
柔性作业车间调度问题(FJSP)是制造系统中一种典型的生产方式。本文研究的包含同速并行机的部分柔性作业车间可描述为:N个工件在M个机台上加工,每个工件包含若干按序排列的工序,工件n的工序总数为 Pn,工件n的工序p有对应的加工机台集 Mnp, Mnp内的机台对工件n的工序p的加工时间为tnp。每道工序需要安排在某一台机器上进行加工。Cnp表示工件n工序p的完工时间。
本文基于以下假设条件:
1) 工件加工顺序、可加工机台集及加工时间已知且固定;
2) 一个机台同时只能加工一个工件,一个工件同时只能被一个机台加工;
3) 不考虑切换时间、运输时间,不考虑生产系统突发情况;
4) 任一工序一旦开始加工则不可中途停止。
以最大化完工时间最小为目标的包含同速并行机的部分FJSP决策变量与数学模型分别如下。

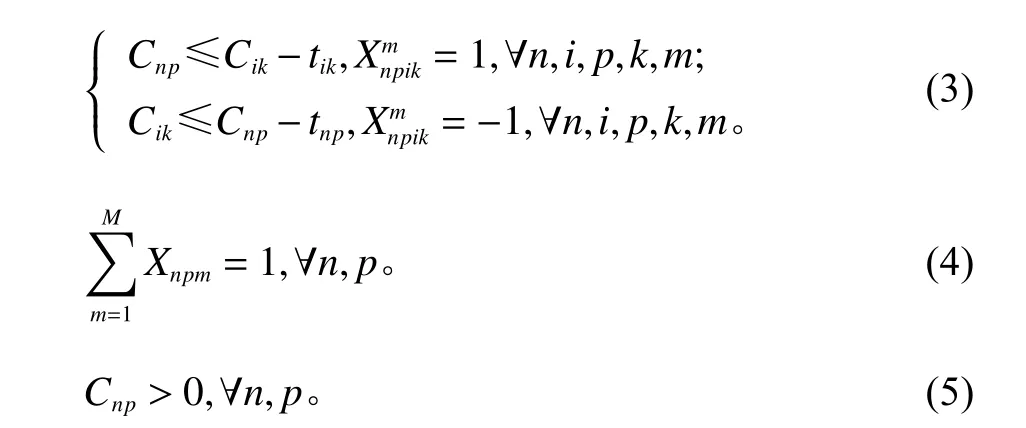
其中 n、i(1≤n,i≤N)代 表工件, m(1≤m≤M)代表机台, p、k(1≤p,k≤Pn)代表工件n的工序。式(1)表示目标函数为最小化最大完成时间;约束(2)表示每个工件都需要按照工序顺序生产,前工序完成时间需不大于后工序开始时间;约束(3)表示同一机台同一时间只能加工一个工件;约束(4)表示每个工件的每个工序只能选择一个机台进行加工;约束( 5)表示工件完工时间均为正数。
2 基于离散Lévy flight策略的混合遗传算法
本文设计的基于离散Lévy flight的混合遗传算法具体流程框架如图2所示。该改进算法使用了基于工序编码基因串的交叉策略与单点变异策略,对每一代的精英解使用了基于离散Lévy flight的随机搜索策略,可改善遗传算法局部搜索能力较弱的缺点,同时也在一定程度上增强了算法的全局搜索能力。
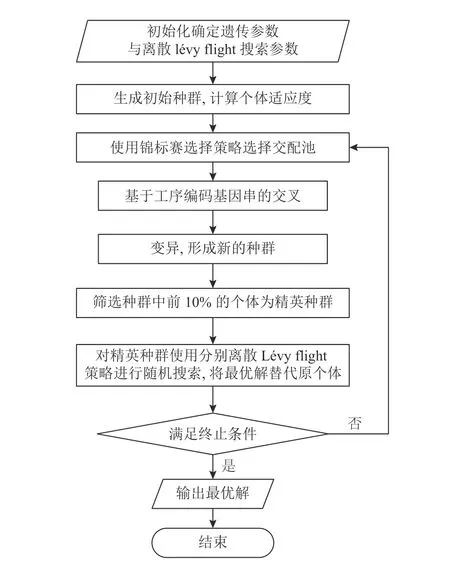
图2 Lévy-GA流程图Figure 2 Flow chart of Lévy-GA
2.1 编码与适应度计算
FJSP需要确定工序的加工顺序与每道工序对应的加工机台。本文采用的编码由工序加工顺序与对应工序加工机台两部分组成。编码示意图见图3。编码由两层组成,第1层为工序加工顺序对应的染色体编码,“213131321”中的第1个“2”表示工件2的第1个工序,第1个“1”表示工件1的第1个工序,第2个“2”表示工件2的第2个工序,以此类推,形成整个问题的工序加工顺序的可行解。染色体第2层为第1层对应工序选择的加工机台,例如,第2个工件的第1个工序选择M2机台进行加工,第1个工件的第1个工序选择M2机台进行加工。每个染色体都对应1个可行解,该可行解使用插入式贪婪解码算法[15]进行个体适应度求解。个体适应度代表当前可行解的目标函数,目标函数越小,说明个体适应度越好。
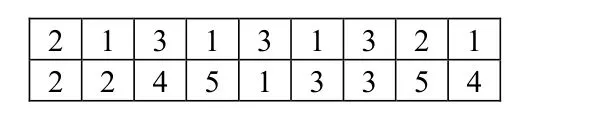
图3 染色体编码方法Figure 3 The encoding method of the chromosome
2.2 交叉与变异操作
交叉与变异操作模仿了生物遗传进化的过程。交叉操作可使2个个体随机交换部分基因,期望将有益的基因组合;变异操作可使个体随机修改某些基因,期望产生适应度更好的个体。本文采用基因串组合交叉策略如图4所示。本文使用的交叉策略操作流程如下。将工件随机分到集合J1或者J2,在父代1中将J1包含的工件对应的工序及机台位置直接继承给子代1,将父代2中J2包含的工件对应的工序及机台按相对顺序先后插入子代1的空余位置,形成完整的子代个体1。同理,在父代2中将J2包含的工件对应的工序及机台位置直接继承给子代2,将父代1中J1包含的工件对应的工序及机台按相对顺序先后插入子代2的空余位置,形成完整的子代个体2。
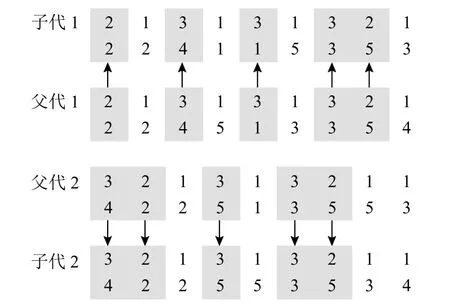
图4 交叉策略示意图Figure 4 The crossover of chromosome
本文采用基于工序基因串和基于机台基因串的变异策略,如图5所示。基于工序基因串的变异策略操作流程为随机生成小于基因串长度的2个正数a、b,选择位置a对应的工序作为变异工序,将其挪至位置b。基于机台基因串的变异策略操作流程为随机生成小于基因串长度的正数c,将位置c对应的机台替换为该工序对应可加工机台集中的其他任意机台。
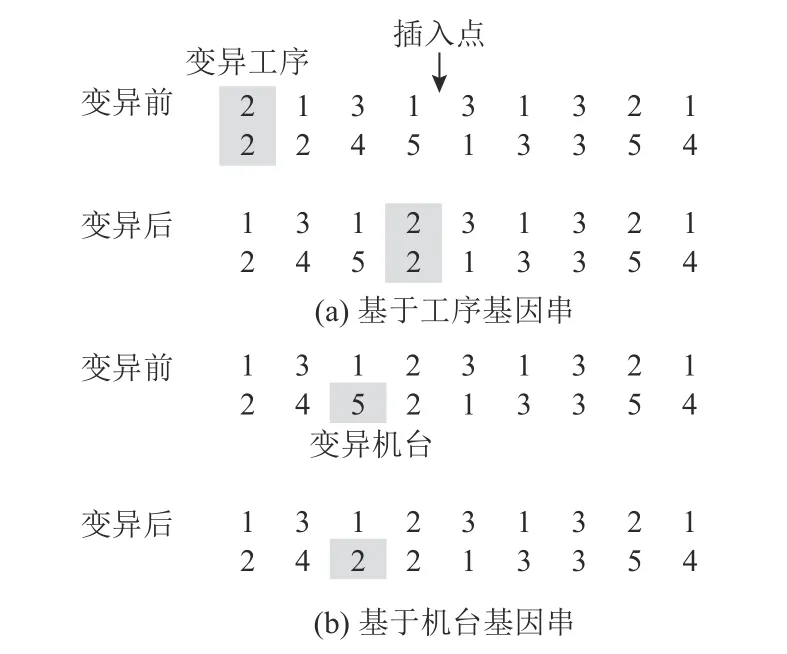
图5 变异策略示意图Figure 5 The mutation of chromosome
2.3 离散Lévy flight策略
Lévy flight属于一种随机搜索策略,Lévy flight的步长分布为满足一个厚尾的稳定分布,由Lévy flight产生的随机步长大概率为小步长,但也有一定概率的大步长游走。大的步长易于搜索全局最优,小的步长有助于提高搜索精度。本文对经过遗传操作后产生的最优个体经过T次具有Lévy flight特征的随机搜索,将随机搜索后的t个个体适应度函数与最优个体进行比较并择优替代。每次随机搜索过程的步长参考Lévy flight搜索策略进行确定,连续Lévy flight搜索策略一般通过Mantegna算法确定步长[16]。本文将Mantegna算法离散化以计算该问题中每次随机搜索的步长S,形成了针对离散优化问题的Lévy flight随机搜索策略。
为简化算法框架,本文使用的邻域游走策略与变异策略相同,每次邻域游走的单位为1,步长S代表邻域游走次数。如果S=2,则代表对应个体进行两次邻域游走。步长S的计算公式为
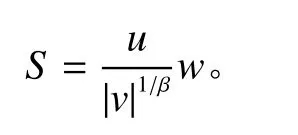
其中,β为[1, 2]中的一个参数,本文取β =1.5; w根据问题规模而变动,一般取步长影响因子 α =80; u和 v 服从正态分布: u ∼N(1,1), v∼N(1,4)。
本文所提出的针对离散优化问题的Lévy flight随机搜索策略伪代码如下。
算法1离散Lévy flight策略
1: For j=1:Psize*0.2 %对前20%的精英个体进行随机搜索与优化,记为pj
2: For i=1:T %对每个个体执行随机搜索T次,记为pi
3: S =u/|v|^( 1/β)*w; %生成随机搜索步长
5: For j=1 to S do %执行随机搜索
7: insert pj(:,a) after pj(:,b); %执行工序调整
9: pj(2,c)=randi(Mnp,1); %执行机台选择调整
10: End
11: best_pi(i); %计算pi适应度
12: End
13: best=min(best_pi,pj);%从随机搜索个体与原个体pj中寻优
14: End
Lévy flight随机搜索策略应用在GA中的核心优点体现在:1) 该搜索策略与GA框架的适配性很高,通过简单的操作弥补GA局部搜索能力较弱的缺陷,仅通过一个参数(步长S)就能控制局部与全局搜索;2) 该混合算法保持种群多样性的能力极强。当种群中出现大量重复个体时,Lévy flight随机搜索策略能对这些个体分别进行邻域搜索和小概率全局搜索,保证种群多样性。
3 实验设计与结果分析
本节通过比较其他算法求解FJSP的结果来验证Lévy-GA的性能。CS、TLBO和GA是目前比较流行的搜索算法,被认为是邻域搜索和种群搜索中高效且经典的方法,已被用于解决许多组合优化问题,因此本文将以上3种算法作为对比算法。除此之外,为了客观评估离散Lévy flight策略的通用性,本文将该策略用于TLBO中,形成了Lévy-TLBO混合算法,所有实验案例均分别使用CS、TLBO、Lévy-TLBO、GA和Lévy-GA进行求解并比较求解结果。本文所使用的算法均采用Matlab R2017a软件进行编码,实验环境为Intel®CoreTM2 Quad 1.6 GHz CPU和8G RAM个人计算机。
3.1 案例设计与参数设置
为验证算法的优化性能是否稳定,优化效果是否显著,设计不同规模与特征的测试问题集,使用CS、TLBO和GA等典型算法与Lévy-GA的求解结果进行比较,以验证Lévy-GA的有效性。在柔性作业类型的车间中,工件数量、工件工序数量及可加工机台集都是影响调度问题特性与规模的重要变量。本节实验对以上3个变量设置了不同规模的变量取值区间,可生成3×3×3=27个不同规模与特性的调度问题。例如,A_A_A代表n_Pn_ Mnp的数据取值区间分别为[4,9],[2,5],[1,4],为各规模问题分别随机生成2例满足以下区间约束的生产数据案例,如表1所示,表中区间约束均为均匀分布。
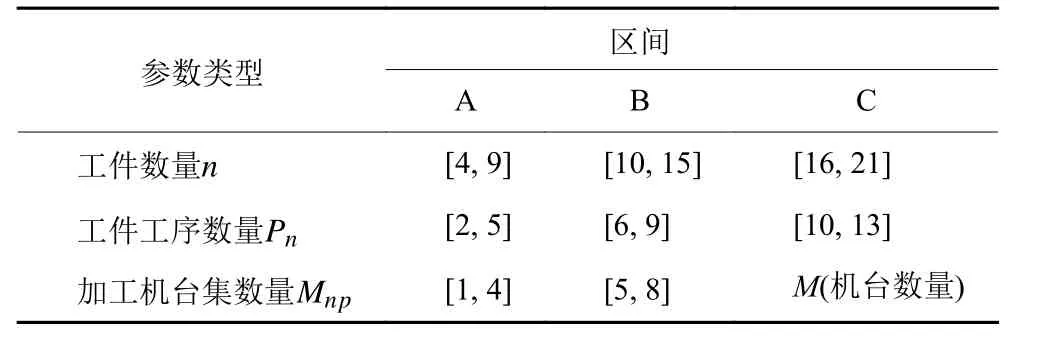
表1 测试问题集实验数据区间Table 1 The relation data intervals of examples
本文提出的Lévy-GA算法,影响算法性能的参数主要有种群数量Psize、交叉概率pc、变异概率pm及Lévy flight搜索步长的步长影响因子α。针对以上关键参数,从27个规模的随机案例中各抽取一组作为参数整定的测试数据集,采用实验设计方法(design od experiment, DOE)进行实验分析,并研究参数对算法性能的影响,从而确定算法的最优参数设置。为保证实验的公平性,对其他经典对比算法的参数设置也进行了相同实验,并形成最优参数。表2分别给出了所有对比算法的最优参数配置,其中Lévy-TLBO的自学因子参数使用离散Lévy flight策略中的随机搜索步长表示。

表2 各对比算法最优参数配置Table 2 The best parameter value for each algorithm
3.2 测试结果与优胜率
为了验证Lévy-GA的有效性,将其同CS、TLBO和GA等典型元启发式算法及Lévy-TLBO混合算法进行了对比。5种算法在27×2 = 54个算例上分别运行20次。记录各个算法在不同案例上使用相同的运行时间经过20次独立运行后所得目标值的最优值、平均值,并统计Lévy-GA相对于其他4种对比算法的改进幅度,最优结果使用粗体突出显示。表3中的最后一行总结了本文所提出算法相较于其他算法的优胜比率。
3.3 性能分析
3.3.1 性能分析与比较
1) 求解质量。
与4种对比算法相比,Lévy-GA算法在所有算例中都可以得到最佳的目标最优值和平均值,如表3与表4所示。在处理小规模案例时(如“A_A_X”“B_A_X”等),CS与其他算法的差距已经开始显现,但GA与所提出算法的最优解差距往往较小。针对个别算例(“A_A_A_2”),所有对比算法均可达到最优值。当问题规模增大后(如“C_X_X”“X_C_X”等),可以明显看出Lévy-GA得到的最优解与均解质量远优于其他对比算法。表4中的统计也可证明所提出的算法在求解大规模问题上的优势。这是由于遗传算法在加入离散Lévy flight搜索策略后,算法可在保证全局搜索的基础上,加强精英个体局部搜索的能力,使整个种群持续进化的能力更强。
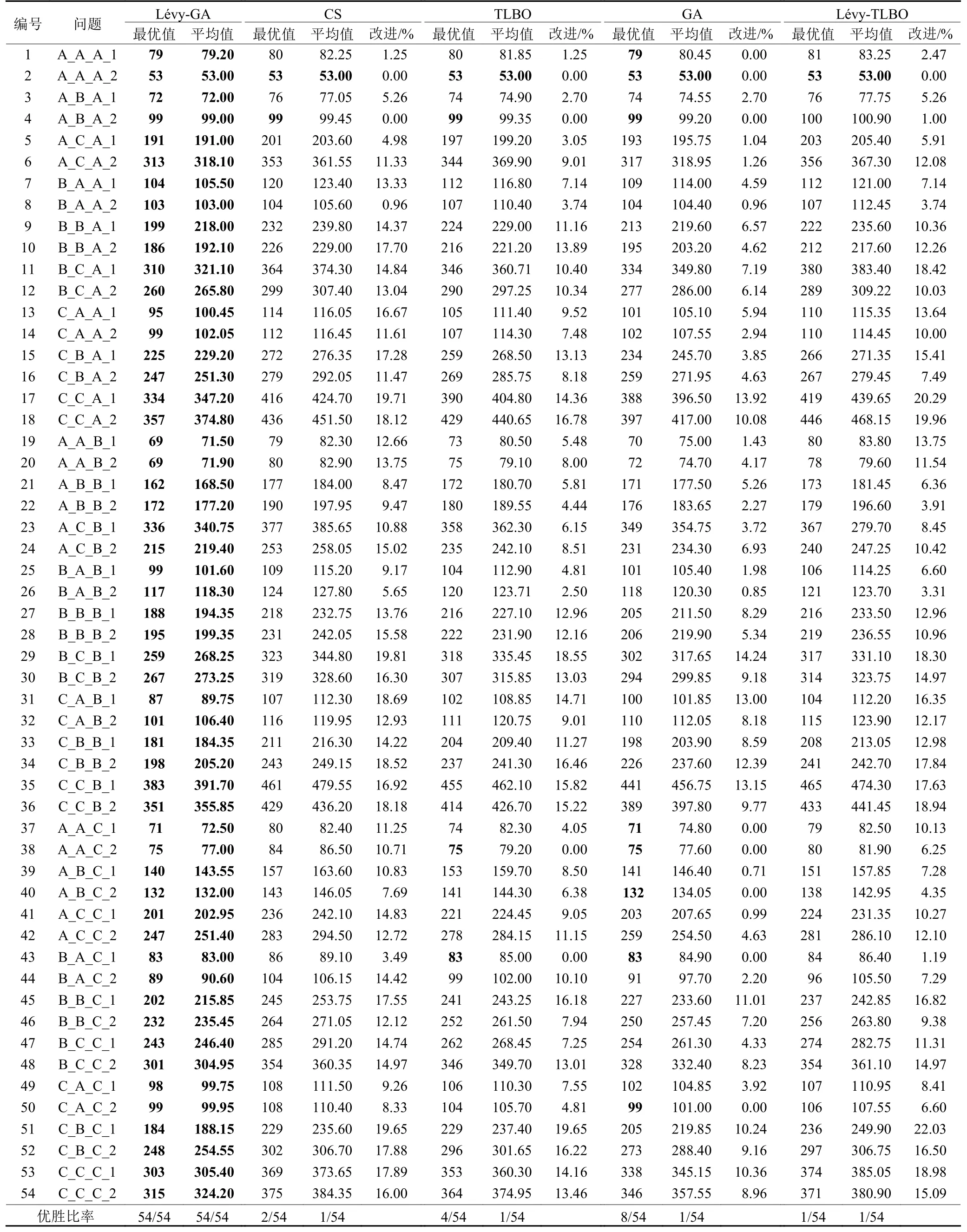
表3 测试问题集实验结果与比较Table 3 Results and comparisons of 54 test problems
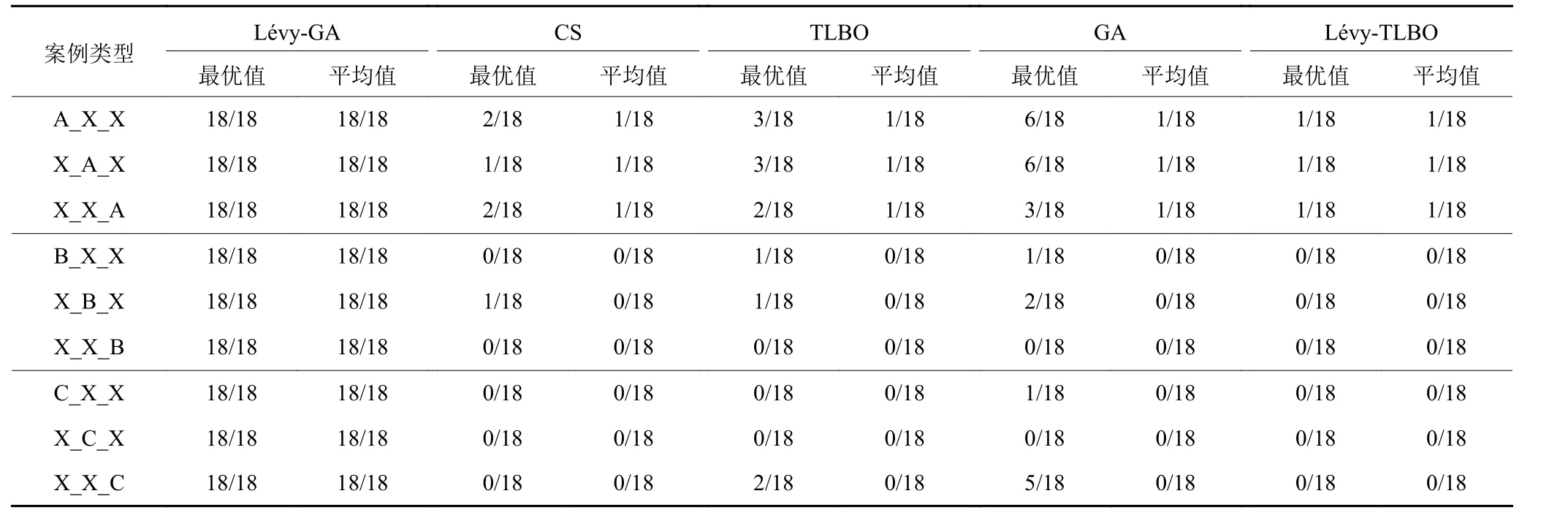
表4 不同规模案例优胜比率Table 4 Superior rate of tests with different scales
2) 收敛性。
离散Lévy flight搜索策略只针对部分精英个体进行随机搜索,虽然搜索过程并不繁琐,但仍然使Lévy-GA的迭代速度相较于GA仅下降了约20%。尽管如此,由于随机搜索过程的高效性,相较于其他对比算法,Lévy-GA依然保证了相对优越的收敛速度,能够有效应用于FJSP及其他组合优化问题中。为更直观展现与比较5种算法的收敛效果,本节利用收敛曲线对不同算法在相同运行时间下的收敛速度进行评价,同时展示算法逼近最优解的过程。选择“B_C_A_2”“C_C_A_2”“A_A_B_2”“B_A_B_1”这4个算例并作出算法CS、TLBO、Lévy-TLBO、GA和Lévy-GA的收敛曲线。由图6可知,在相同运行时间内,Lévy-GA均能以较快的速度收敛且获得最优的目标函数值。因此,可直观看出Lévy-GA算法的收敛速度与收敛结果均优于其他4种对比算法。
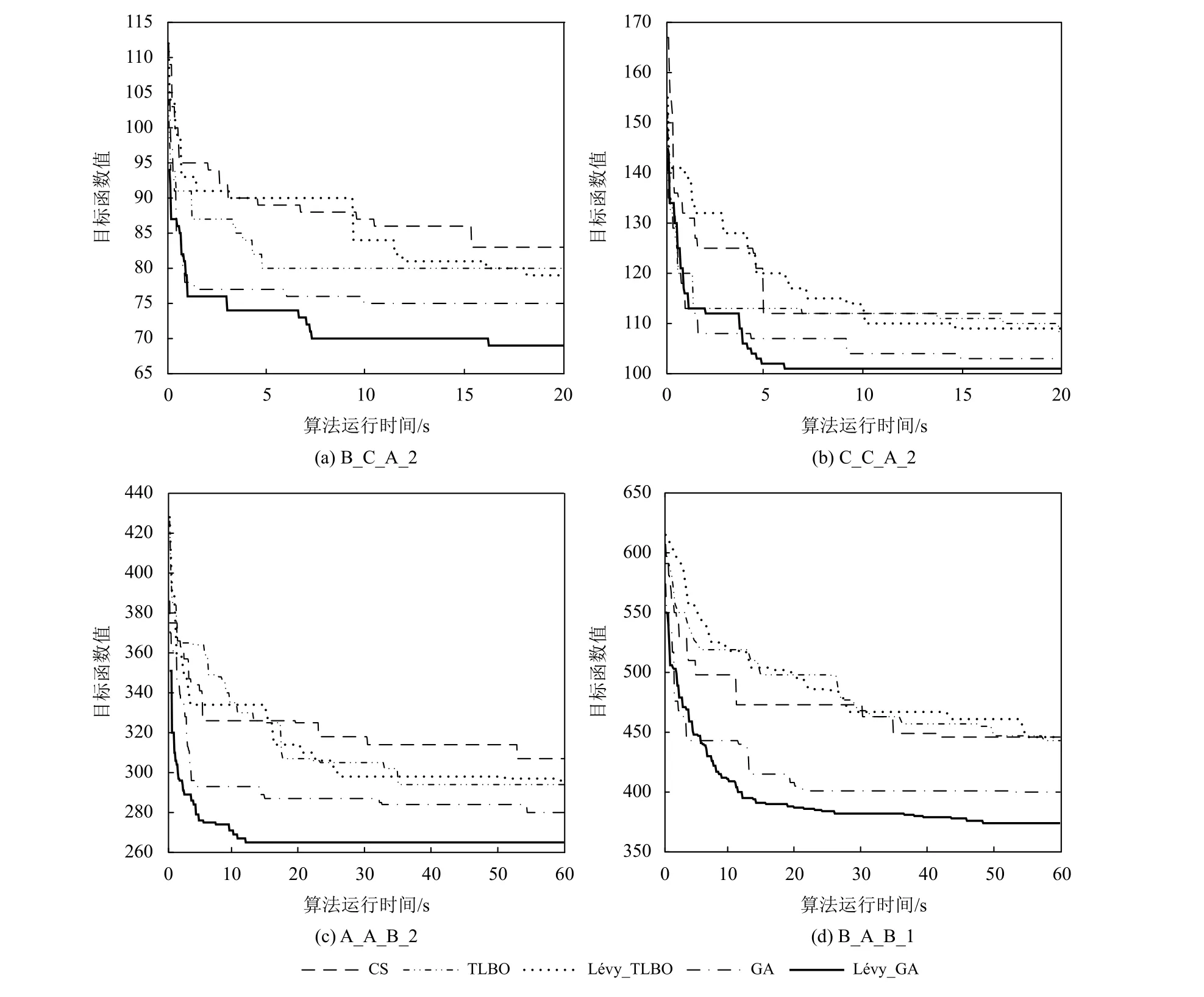
图6 不同算例收敛曲线比较图Figure 6 Convergence curves comparison of different tests
3) 稳定性分析。
表3记录每个算法求解不同算例得到的最优值与运行20次获得的均值。当均值越靠近最优值,则代表算法稳定性越好,即(c指案例编号)越小越好。计算各个算法求解的所有案例的均值 µc并定义稳定性参数为当稳定性参数 ω越小,代表该算法运行结果越稳定,如表5所示。从表5中可知,CS、GA与Lévy-TLBO稳定性相当且均强于TLBO,Lévy-GA的稳定性强于其他对比算法。这是由于GA本身具有强大的全局搜索能力,在加入Lévy flight策略后,算法的局部搜索和全局搜索能力同时得到了增强,故相较于其他算法其搜索性能更加稳定,算法鲁棒性也更强。

表5 算法的稳定性参数Table 5 The stability parameters of algorithms
另一方面,通过表3可进一步发现,Lévy flight策略并非在所有算法中均能取得较好的效果。Lévy flight策略在遗传算法中使用时,保证了遗传框架全局搜索能力并增强了局部与全局搜索能力,从而帮助精英种群更快寻优。而将其使用在TLBO这种本身就具备个体局部寻优策略的算法中时,扰乱了算法原本的进化过程,不能取得显著的搜索效果,反而降低算法的迭代速度(迭代速度下降约40),对算法收敛效果带来消极影响。
图7与图8分别为Lévy-GA算法求解算例C_B_C_1(n=16,m=10)输出的最佳调度甘特图、最优解与群体均值进化曲线。从进化曲线中可看出,所提出算法针对较大规模的调度问题具有较快的收敛速度,群体进化能力强且进化过程稳定,能够快速获得全局最优解。
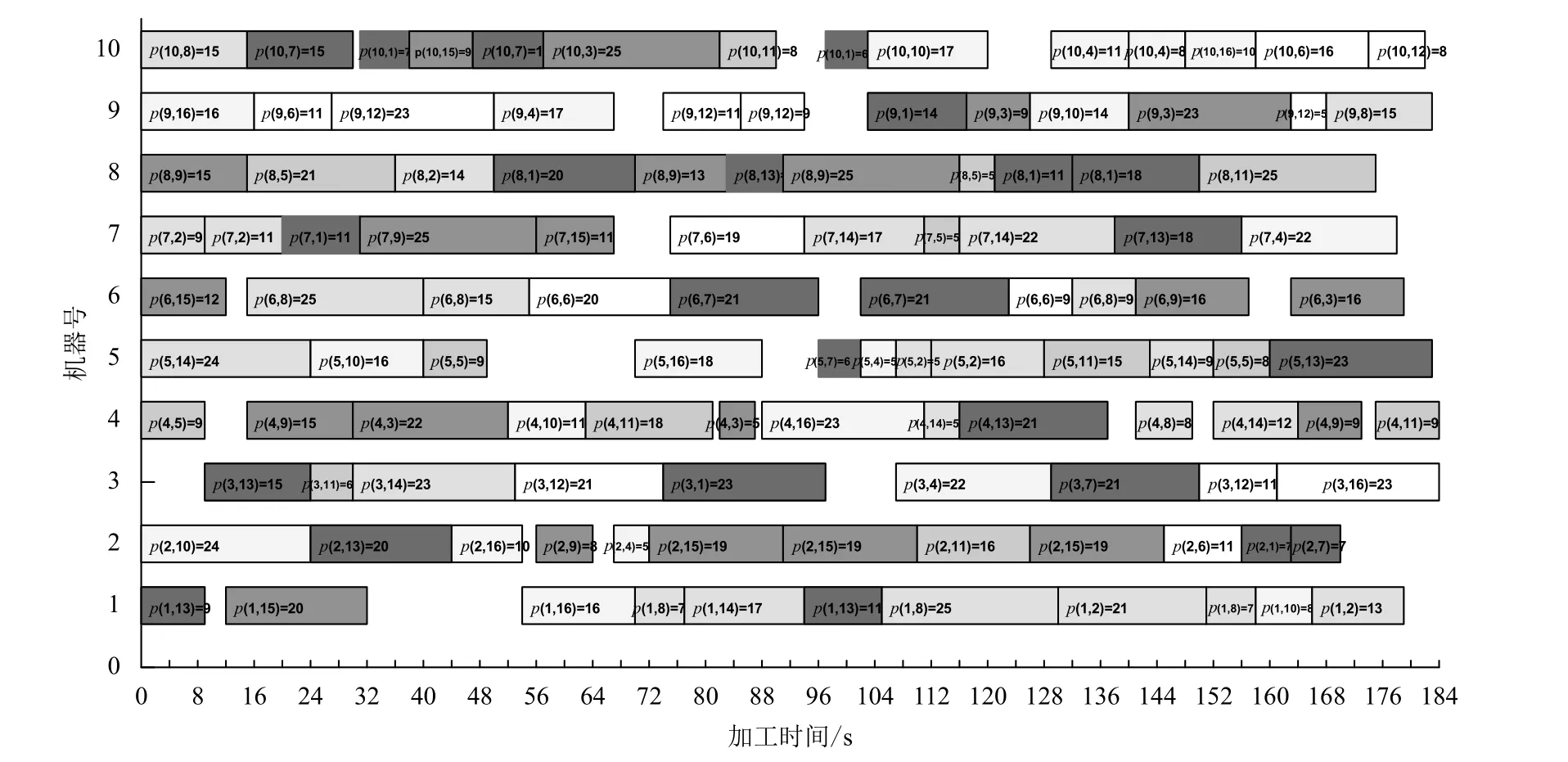
图7 算例C_B_C_1最佳调度甘特图Figure 7 Gantt chart of the result for test C_B_C_1
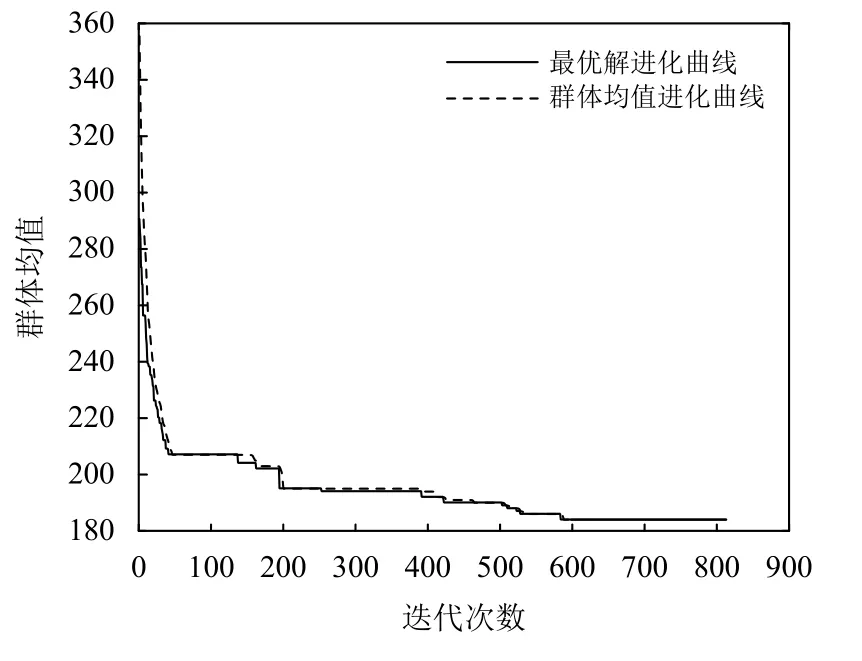
图8 算例C_B_C_1最优解与群体均值进化曲线Figure 8 Optimization curve and mean curve of test C_B_C_1
3.3.2 适配案例分析
为验证算法的适配案例,使用控制变量法分析每个变量不同规模的案例的求解性能,结果如表6所示。“X_A_X”表示工件数量为水平A的18个案例,每一行对应的数据表示Lévy-GA相对于4个对比算法在该水平所有案例上改进比例的均值。通过分析表6发现,在所有类型案例下,Lévy-GA的求解结果均不同程度强于4种对比算法。其中,通过纵向对比案例类型“A_X_X”“B_X_X”和“C_X_X”的改进结果可知,当保持其他变量不变,工件数量 n增加时,Lévy-GA的优化效果越来越好。同理,当工件工序长度 Pn发生变化时,其他变量保持不变时,Lévy-GA的优化效果也是逐渐增强。当可选机台集规模 Mnp发生变化时,Lévy-GA的优化效果依然强于其他对比算法,但在与TLBO、GA和Lévy-TLBO进行比较时,并未发现优化效果持续增强的趋势。因此,通过对不同案例类型、规模及算法相应求解效果的比较与分析得出,Lévy-GA相较于4个对比算法来说,更适合求解大规模FJSP,特别是包含大规模工件或长工艺路径的FJSP。
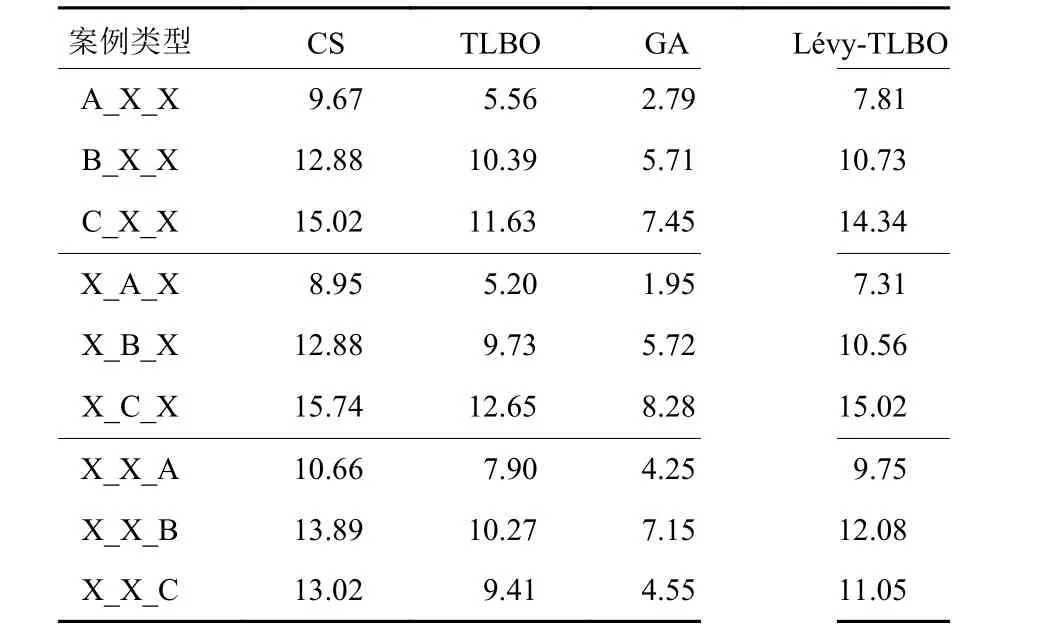
表6 Lévy-GA相较于对比算法改进率Table 6 Improvement rate of Lévy-GA %
4 结论
柔性作业车间调度问题是比较经典的一类组合优化问题,也是典型的NP难问题,本文研究了具有同速并行机的部分柔性作业车间调度问题,提出一种离散Lévy flight策略的混合遗传算法进行求解。该混合算法通过使用离散Lévy flight搜索策略对每代精英种群进行变步长搜索,可提高算法的局部搜索能力,增强种群多样性。
为验证算法性能,本文设计27组不同规模的测试问题集,每个问题集中各包含2组算例。将CS、GA和TLBO等经典算法作为对比算法,对不同规模的54个FJSP算例进行实验并分析实验结果。结果显示,Lévy-GA在求解大规模问题时得到的最优解远远优于其他对比算法。通过对算法性能进行分析比较,发现Lévy-GA在求解质量、收敛效果与稳定性上强于其他算法;使用控制变量法分析不同规模下的工件数量、工件工序数量及可加工机台集案例,证实了Lévy-GA更适合求解大规模FJSP,特别是包含大规模工件或长工艺路径的FJSP。

