网格结构对Pneu-Net软体驱动器的弯曲性能影响规律研究

田 亮，韩奉林，李明辉，刘 伟，严宏志,3

（1.中南大学 轻合金研究院，长沙 410012；2.中南大学 机电工程学院，长沙 410012；3.高性能复杂制造国家重点实验室，长沙 410012）

0 引言

由硅胶制成的软件机器人在医疗、救援、工业生产等领域有广阔的应用前景[1]。软体机器人的驱动方式主要包括压缩流体、SMA（Shape Memory Alloy，形状记忆合金）、EAP（Electromechanically Active Polymer，电活性聚合物）等，其中以压缩流体为动力源的软体机器人由于具有结构简单、控制方便、驱动能力强等优势，获得了广泛的关注[2]。

根据结构特点，现有流体驱动软体致动器可以分为两大类：第一类是纤维增强型，其中最为著名的是McKibben型气动人工肌肉，但单个McKibben型驱动器只能实现一维的伸展驱动[3,4]，通过改变纤维的布置方式，可以实现弯曲、扭转等复杂运动模式。另外一类是Pneu-Net（Pneumatic Network，气动网格）结构，即在弹性聚合物结构中布置特定形状的网状腔格，在气压作用下，软体结构内部产生非均匀的应变，从而产生宏观变形运动。Pneu-Net软体驱动器在小压力下即可实现较大的变形，具有更好的顺应性[5]。

弯曲驱动器是实现抓手、行走机器人等复杂机器人的基础构件，因此得到更多的研究。应用Pneu-Net原理，Whitesides的团队首先在条状硅胶内嵌若干矩形截面空腔，充气后可实现弯曲变形[6]，基于这种原理制备了一个软体抓手[7]。后续他们发现如果去除各空腔之间的部分连接材料，使驱动器具有若干个离散的驱动气囊，就可以大幅提高驱动器的响应速度及弯曲角度[8]，如图1(a)所示，Walimoto等也曾经设计过类似的离散气囊驱动软体弯曲驱动器[9]。

随后这种褶皱状的Pneu-Net气动弯曲驱动器得到广泛的推广和应用，但气囊的横纵截面结构形式又各有不同。与Whitesides团队提出的最初始方案相似，Katzschmann等利用矩形截面气囊制作了一个软体平面抓手，并与另外6个气囊协作构成了一个7自由度软体机械臂[10]，如图1(b)所示，Pang利用两个矩形截面气囊结构制作了一个可以转弯仿尺蠖爬行机器人，如图1(c)所示[11]。

有研究者改变驱动器的纵截面形状，通过沿宽度方向横向拉伸设计制备了一些新的Pneu-Net结构。Yap等利用低成本的FDM（Fused Deposition Modeling,熔融沉积）3D打印的方法制备了一种可以产生较大输出力的双向弯曲驱动器[4]，如图1(d)所示，气囊形状为横向的半圆柱。Walimoto等分别设计了纵截面类似于正弦和方波曲线的软体结构，制造了一个微型的软体抓手[9]，如图1(e)所示。Helps和Rossiter设计制造了具有三角锯齿状气囊的弯曲驱动器[12]，如图1(f)所示。

改变气囊横截面形状，或同时改变气囊的横、纵截面形状，可得到更为复杂的气囊形状。Alici等所设计的弯曲驱动器中气囊类似于纵向半圆柱[13]，如图1(g)所示。Zatopa等设计了具有圆柱与圆锥结合形状气囊的驱动器，并应用于软体章鱼触手[14]，如图1(h)所示。Scharff等通过3D打印方法制备了具有复杂三维结构的软体型腔[15]，如图1(i)所示。

图1 具有不同形状气囊的Pneu-Net驱动器

这些形态各异的Pneu-Net驱动器均具有弯曲运动能力，但哪种气囊形状带来的弯曲性能更好？结构参数的大小又如何影响总体的弯曲性能？为回答这些问题，本文将对不同类型气囊的弯曲性能进行对比分析，研究气囊几何结构参数对弯曲性能的影响规律，以期对离散气囊Pneu-Net弯曲驱动器的设计提供理论依据。

1 材料与方法

1.1 研究对象

在以往的研究中，往往注重驱动器整体性能的评估，直接把具有多个气囊的弯曲驱动器作为研究对象。本研究为更加细致地区分单气囊独立弯曲以及多气囊的协同弯曲效应，将首先研究仅包含一个气囊的单气囊驱动器，然后再研究包括两个气囊的双气囊驱动器。

利用单气囊模型着重分析气囊结构形式和结构尺寸变化对弯曲性能的影响规律。参照现有文献中气囊的结构形式，选取矩形（Rectangular，简写Rec）、纵向圆柱（Longitudinal cylinder，简写LCY）、三角（Triangular，简写Tr）及横向圆柱（Transverse cylinder，简写TCY）四种气囊形式为研究对象，如图2所示。为避免边界影响气囊变形，将气囊置于一个70mm的矩形管的中部。为使研究结果具备可比性，四种气囊具有相同的表面积，确保在制备时将使用等量的材料。Whitesides团队提出的Pneu-Net驱动器利用了两种效应产生弯曲变形，分别是气囊形式的结构设计和底部的应变限制层[6]，本文目的是研究气囊结构的影响，因此未给矩形管加入应变限制层。

图2 单气囊模型结构示意图（图中已标注尺寸单位均为mm）

双气囊模型中包含两个气囊，主要用于分析气囊之间的相互影响以及气囊分布方式对于其总体弯曲效果的影响规律。与单气囊模型一样，双气囊也分布于长70mm的矩形管上。

所有模型的材料均选用EcoflexTM00-30（Smoothon-Inc.TM，PA，USA）。这种材料可以承受很大的应变，成型方法较简单，在软体机器人的制备中得到了广泛的应用。

1.2 有限元分析方法

软体机器人的变形中涉及到超弹性材料、大位移、大应变等非线性因素，解析建模存在很大的困难，对于具有复杂几何结构的Pneu-Net驱动器来说更是如此。非线性有限元仿真方法可以克服上述难题，已经被广泛应用于软体机器人的变形模拟。

软体机器人采用的硅胶材料属于超弹性材料，其应力应变之间具有非线性对应关系，但可以用应变能密度函数准确描述力学行为。在本文的仿真中，EcoflexTM00-30材料采用3阶Ogden超弹本构模型进行描述，参照文献[16]。本构模型系数取值如下，μ1=1.88kPa、μ2=2.225kPa、μ3=1.887kPa、α1=-3.848、α1=0.6632、α1=4.225、D1=2.9259MPa-1、D2=D3=0。

网格尺寸对求解精度和求解效率有很大的影响，为了获得合理的尺寸值，选取单矩形气囊模型进行了测试求解。在测试中，逐步加密网格，当驱动器变形结果不再随网格尺寸变化而变化时，即认定为合理的网格尺寸。

由于本文不涉及驱动气体的动力学效应，因此驱动条件简化为直接在气囊内表面施加相应压力，这种方法在以往的仿真中也得到了应用。为了避免不收敛的问题，压力设置为按照斜坡函数缓慢施加。

驱动器边界条件设置为矩形气管一端固定、一端自由。因为本文主要关注稳态响应，对变形和应变的计算精度有较高要求，因此采用了隐式求解方法，并在计算中考虑接触及大变形等非线性效应，同时在划分网格后选取如图3所示的底部边线节点集。在后处理中，将以此节点集为路径，给出计算结果的分布规律。后处理中采用的坐标系的方向如图3所示。

图3 有限元模型及结果坐标系定义

2 结果与讨论

2.1 有限元分析方法验证

为获得合理的网格尺寸，以Rec气囊模型为对象进行测试性计算。驱动器施加压力大小为10kPa，网格尺寸变化范围为0.1mm～2.5mm，变化步距为0.1mm。图4给出了末端位移及计算时间随网格尺寸的变化规律，当网格尺寸取0.1mm、0.2mm时，仿真因占用内存过多而报错。从中可以看出随着网格尺寸的减小，端点的y向位移有不断增加的趋势，但当网格尺寸小于0.7mm后，末端位移渐趋稳定。计算时间随网格密度的提高显著增加，网格尺寸为0.3mm的计算时间约为64.5min,是0.5mm时的9.63倍（仿真的硬件条件为：CPU Intel Xeon Gold 6230 40核、内存64G）。综合考虑精度和效率两方面因素，本文在后续研究中的网格密度均设置为0.5mm。

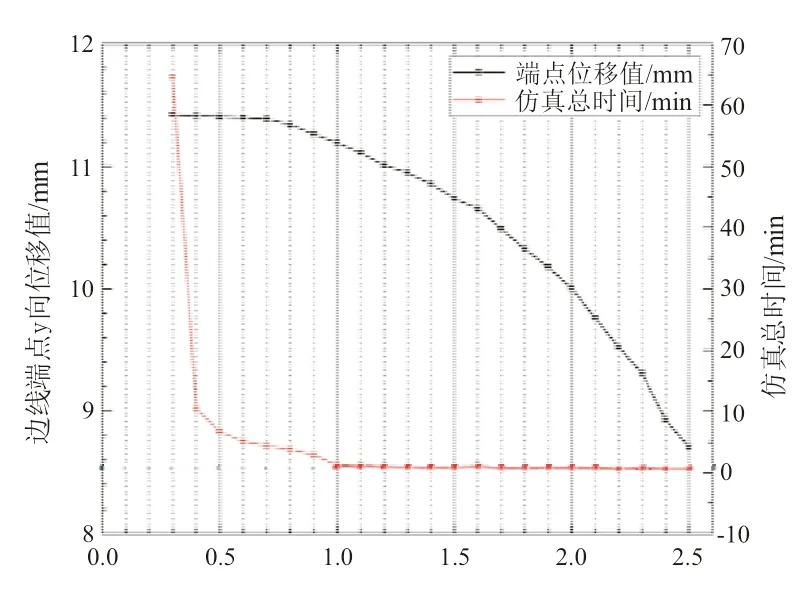
图4 网格尺寸对末端y位移计算结果及计算时间的影响规律

2.2 气囊形状对驱动器弯曲的影响

为了评估气囊形状对软体驱动器弯曲性能的影响，对1.1节所述的四个不同的单模块驱动器进行仿真分析。

图5给出了驱动器左端固定、右端自由、内部充气压力为10kPa条件下，各驱动器边线上各节点的y向位移。从中可以发现，各驱动器在气囊所在的区间（25＜x＜45）曲率最大，说明气囊在弯曲驱动器中起核心作用。驱动器在临近左侧固定端部附近有微小的弯曲变形，但经过小段距离后，位移几乎不变。微幅波动的原因是软体驱动器在固定端附近产生了局部变形，而本文所研究的单模块驱动器左侧留有足够的长度，这种边界引起的局部变形不会对气囊产生的弯曲变形产生干扰。气囊右侧的曲线呈直线状态，说明驱动器气囊右侧没有产生弯曲变形，但这段直线可对气囊产生的微小弯角起到放大作用，从而较明显地观察到不同形状所产生弯曲的差别。

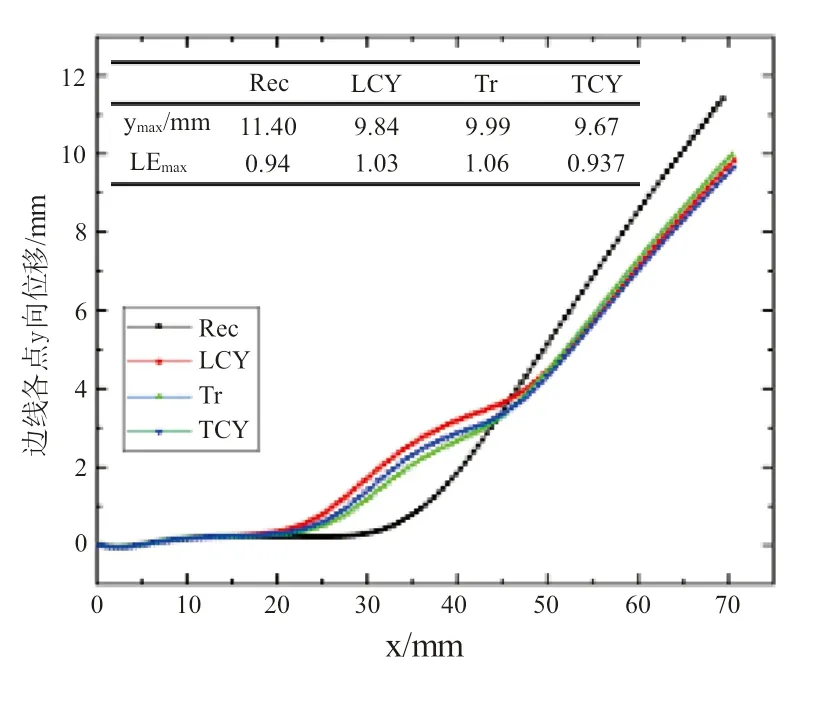
图5 沿驱动器底部边线的y向位移分布

在所研究的四种气囊中，矩形气囊所产生的总体弯曲最为明显，三角形气囊其次，圆柱状气囊效果较差。在气囊所在局部区间，四种气囊所引起的弯曲变形差异更加显著。其中，矩形气囊引起的曲率变化比较平缓，驱动器的弯角缓慢增加，在气囊中部可以产生最为明显的弯曲。纵向圆柱、三角形、横向圆柱气囊因为存在向侧面和底部的膨胀趋势，因此测得的y向位移存在局部负曲率区间。

上述现象可以结合图6来获得解释。当气压P作用在驱动器上时，在沿驱动器长度方向产生一个轴向力F=P.S2，其中S2为气囊沿驱动器轴向的受力面积。Pneu-net驱动器是气囊偏置结构，轴向气动力的等效中心作用点不在驱动器的弯曲中性面上，存在一个偏距e，因此会产生等效的驱动弯矩M=F.e，使得驱动器局部弯曲。而在非气囊段处，驱动器的横截面是对称时，轴向气动力的等效中心作用点在驱动器的弯曲中性面上，驱动器均匀膨胀，不会产生弯曲效果。因此，Pneu-net驱动器弯曲主要集中在气囊段附近，其弯曲程度由两个核心因素控制：驱动弯矩M和抗弯刚度。抗弯刚度除了与材料的弹性模量E相关外，还与截面对中性轴的惯性矩I成正比。假设驱动器弯曲时中性层一直垂直于中间截面，则中性层曲率为：

图6 驱动器变形原理分析

为估算驱动弯矩，可根据截面几何形状计算腔内区域的几何中心距中性轴的距离e，测量出腔内区域面积S2。根据截面几何信息可以直接计算出截面对中性轴的惯性矩I，由表1可以看出，三角形的惯性矩最大，其次是矩形，横向圆柱和纵向圆柱的惯性矩最小。假设驱动器在形变的过程中弹性模量是不变的，则驱动器的曲率正比于λ，计算可得各驱动器中λ最大值为矩形气囊，其次三角形和横向圆柱，最差为纵向圆柱。结合图5，可以看出驱动器在气囊段曲率最大的确实为矩形，其次是三角形和横向圆柱，最小为纵向圆柱。

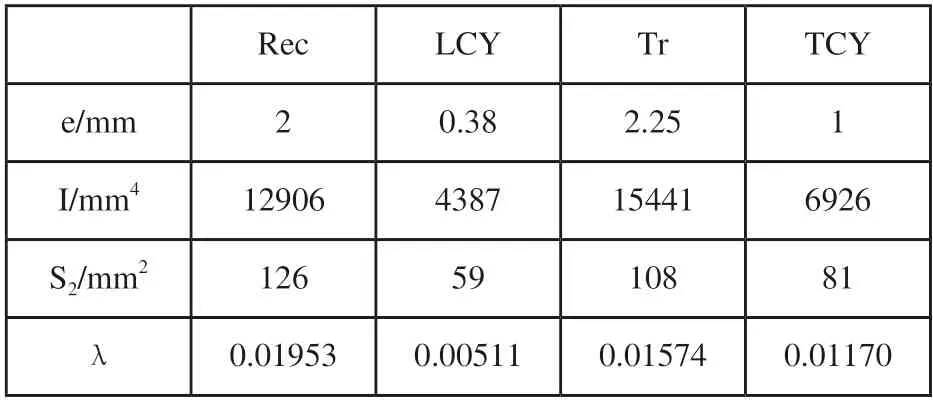
表1 各驱动器的相关参数

2.3 单气囊尺寸因素对驱动器弯曲的影响

针对综合性能较高的矩形截面，分别改变气囊壁厚t、高度h、截面长度l等参数,通过有限元仿真对驱动器的弯曲性能进行了单因素分析。

2.3.1 气囊壁厚t对驱动器弯曲的影响

由图7可得，驱动器的壁厚越大时，端点y向位移值越小，壁厚为1mm的驱动器的末端位移值为27.06mm，为4mm的仅为8.42mm，所以驱动器的弯曲性能随壁厚增加而降低。这是因为当壁厚较小时，气囊侧壁的变形更大，也会带动更多的气囊间隔区域的顶部材料变形，因此驱动器上部材料的伸长更为明显，弯曲程度也更大。

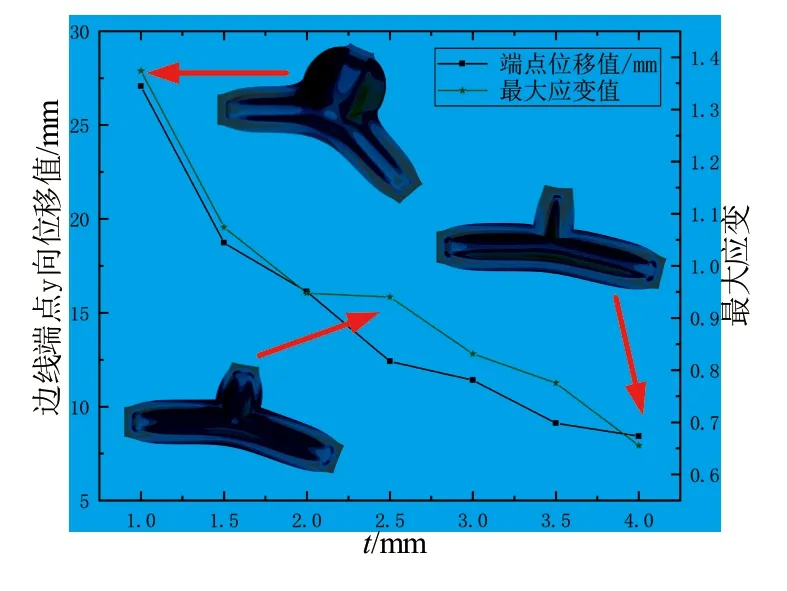
图7 壁厚对端点位移值及最大应变的影响规律

但也应该注意到，当减小壁厚时，驱动器的最大应变会显著增加，从而影响驱动器的使用寿命。因此，在最大应变小于材料的许用应变条件，可以适当减小气囊的壁厚，以增大驱动器的弯曲能力。

2.3.2 气囊高度h对驱动器弯曲的影响

从图8可得，高度h从1mm增至9mm的过程中，驱动器的端点y向位移值和最大应变均随着气囊高度的增大而增大。但是当h到达10mm后，驱动器的端点位移值和最大应变的增速减缓。

从图8应变曲线可以看出，在高度的增加初期，气囊侧壁的变形比较显著，有利于弯曲性能的提高，但后期应变的增速减缓，所以弯曲程度的增速也放缓。如图6所示，当增加气囊高度时，气囊的侧面面积和抗弯刚度都会增大，但λ值是先增大后减小的。

图8 高度h对端点位移值及最大应变的影响规律

从上述结果和分析可知，虽然增加h可以增大驱动器弯曲能力，但h增加会导致制造材料，本身重量和成本的增加。因此适当增大气囊高度有助于提高驱动器的弯曲性能，但也不是越高越好，需要结合自重、成本等因素综合确定。

2.3.3 气囊截面长度l对驱动器弯曲的影响

从图9可得，气囊截面长度l越大时驱动器弯曲效果越明显。但值得注意的是，l为1mm的驱动器末端点y向位移为9.47mm，l为9mm时为15.61mm，显然末端位移并不随l的增加而呈现正比变化关系。如图9所示，计算弯曲位移与截面长度的比值y/l，可以发现随着气囊截面长度的增加，其单位长度的弯曲变形是在减小。同时，驱动器变形的最大应变，也随相应气囊中间截面段增大，显然提高气囊长度对于使用寿命也不利。

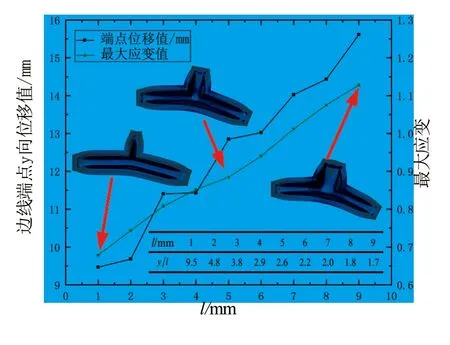
图9 截面长度l对端点位移值及最大应变的影响规律

因此，从提高弯曲能力角度来看，应采用尽量小的气囊截面长度l，但也要注意过小的l会提高变形腔的制备难度。

2.4 气囊布局对驱动器弯曲的影响

Pneu-Net气动网格包含多个气囊，气囊的布局是否会对整体的弯曲性能产生影响？各个气囊对弯曲的贡献是独立的还是相互影响的？为了回答这些问题，通过仿真研究了气囊布局对整体弯曲性能的影响规律。

首先改变气囊间距d，测量驱动器末端的y向位移。由图10可知，当d小于8mm时，驱动器的弯曲程度随d增大而显著提高，这说明气囊之间对弯曲的贡献存在相互影响，气囊间距越近，这种相互之间的耦合效应越强。当d大于8mm后，弯曲能力渐趋稳定。当d=16mm时，总体的变形结果为22.1mm，接近于单个气囊带来弯曲效果的2倍，说明此时气囊之间的耦合效应已经可以忽略。

图10 气囊间距d对端点位移值的影响规律

从仿真结果看，气囊变形的耦合效应将削弱单个气囊造成的弯曲效果，但这并不意味着气动网格中气囊的间距越大越好，因为驱动器的弯曲作用最大有效区域是气囊，气囊之间的联结区域对弯曲的贡献很小，d过大时，虽然可以最大程度发挥单个气囊的作用，但会增加驱动器的长度，总体获得的曲率反而会减小。

图11给出了气囊间距d=16mm时，驱动器底部侧边的y向位移分布及两个气囊所引起的角度弯曲 。从中可以看出，第一个气囊造成的角度变化比第二个气囊大，这说明在Pneu-Net中，各个气囊对弯曲的贡献作用并不是均等一致的。这种现象可以结合图12来说明，在未弯曲或小变形状态下，截面A和截面B上的合力都等于Fend=P.Send，所以两个气囊引起的弯曲变形应该是一致的。但是在大变形状态，截面A上合力除了Fend，还有一个附加的扭矩MA，此扭矩与截面中心距Fend的作用线距离eA有关。显然由于截面B靠近端部，其上的附加扭矩要小很多。所以在气囊原有弯曲效果以及附加扭矩的共同作用下，驱动器在第一个气囊处获得更大的角度。

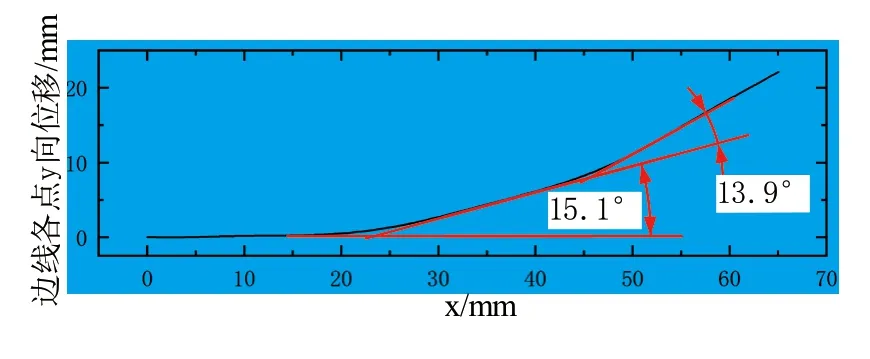
图11 双气囊模型沿驱动器底部边线的y向位移分布

图12 气囊弯曲作用随位置变化的力学原因

根据上述可知，气囊的弯曲作用与所处的位置也有关系。在Pneu-Net驱动器中，各个气囊虽然结构相同，但因为距离端部的距离不同，给驱动器造成的弯曲效果其实也会有差异，因为越靠近固定端，曲率越大。所以在软体机器人建模中常采用的常曲率模型在大变形条件下并不能准确地描述机器人的运动状态。

3 结语

本文采用非线性有限元仿真方法，对Pneu-Net气动网格中气囊结构及布局对总体弯曲效果的影响进行了分析。为突出气囊结构的影响，采用了与其他研究中不同的单气囊和双气囊模型，结论如下：

1）对比分析了矩形、纵向圆柱、三角、横向圆柱等形状的气囊，发现在等量材料条件下，矩形具有最好的弯曲效果；

2）减小壁厚可以有效提高总体弯曲变形程度；增加气囊高度也有提升效果，但超过一定值后提升作用减缓；增加气囊长度虽然可以增加总体弯曲变形，但若考虑单位长度的变形，则可能出现负面效果；

3）Pnue-Net驱动器中各个气囊之间存在变形耦合现象，导致在多气囊条件下，各气囊的实际曲率会小于单个气囊作用的情况；由于大位移非线性作用，气囊产生曲率还与在驱动器的位置有关系，越靠近固定端，弯曲效果越明显，这一现象说明在软体机器人建模中常用的常曲率模型可能存在局限性。