基于不平衡负荷预测的配电网PMU数据谐波检测
胡金东,康宝华
(国网山东省电力公司烟台供电公司,烟台 264000)
0 引言
配电网在电力系统中是非常重要的部分,主要负责接收电能和分配电能,随着社会对电能需求的增大,对于配电网的研究越来越多,在早期研究中,负荷预测在配电网的管理上承担着非常重要的责任,不同负荷具有不同的特征,在不同的时间周期内,呈现出不同的波动特点,在电力事业不断发展的今天,通过负荷预测解决配电网的各项问题已经是比较常见的手段[1]。准确地预测出配电网中的负荷,能够有效减少配电网的操作成本,同时提高能源的利用效率、减少污染排放量[2]。对于配电网PMU数据谐波检测,负荷预测同样能够发挥出自身的优势。
PMU是配电网中的一个相量测量装置,能够实时采集电力数据,为电力系统的运行提供丰富的数据源,准确反映配电网的运行状态信息,为电网的实时分析提供有力的保障[3]。但是受到各种非线性用电设备、不对称故障、不平衡负载等影响就会产生大量谐波,污染配电网环境,谐波的有效检测是保障配电网安全的重要内容[4]。
目前对配电网PMU数据谐波检测的研究,更多的是将状态感知和估计作为重点,利用概率论和相关知识进行假设检验,以一定的逻辑判断PMU数据的量测量,估计状态,通过对状态的辨识实现对谐波的检测。但是随着配电网规模的不断扩大、PMU数据的不断增加,这种谐波检测方法将受到限制,很难实现对谐波源的准确定位,同时又会出现较高的检测误差,检测方法的可靠性需要进一步提高[5]。因此,提出基于不平衡负荷预测的配电网网PMU数据谐波检测,解决上述常规检测方法中存在的问题。
1 基于不平衡负荷预测的配电网PMU数据谐波检测方法设计
1.1 建立短期负荷预测模型
假设存在配电网负荷数据集Q,预处理数据集,统一数据属性,计算公式如下:

式(1)中xi表示数据集Q中的第i负荷数据值,表示预处理后的数据,ximax=max(xi),ximax=min(xi)。在数据预处理完整后,建立短期负荷预测模型,由数据训练结果建立,表示为:

式中xi表示样本的输入,yi表示样本输出结果,si和表示最小化目标函数的最优解,β表示回归系数,H表示数据序列。由式(2)可知,建立的短期负荷预测模型是一个回归目标函数,其最优解表示为为了进一步求得回归决策函数,将最优解代回到式(1)中,获得最终的决策回归方程。
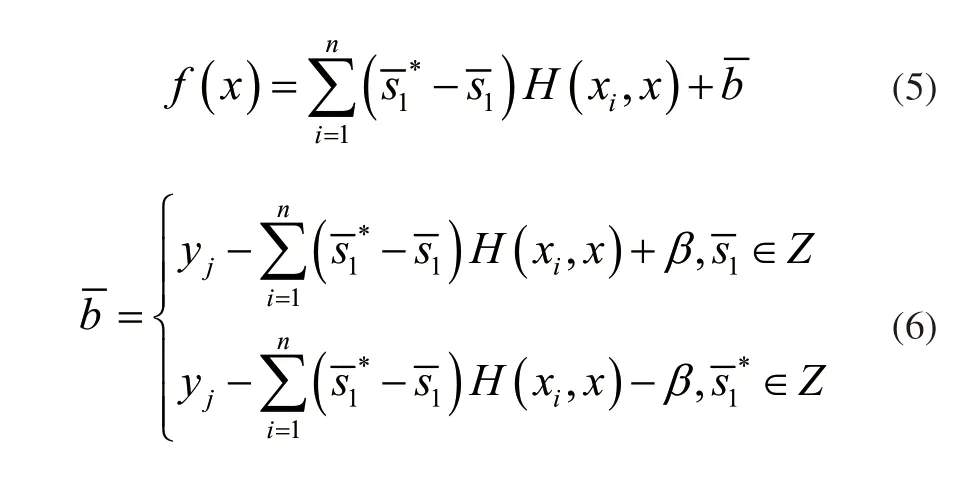
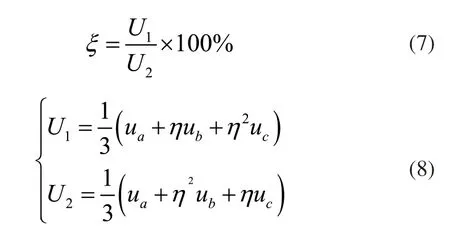
式中η表示旋转算子,U1和U2表示负荷数据的支路分量,ua、ub、uc表示三相电压矢量。在确定负荷数据的不平衡度后,分析负荷数据的线性关系,定位配电网中的谐波源。
1.2 定位谐波源
在配电网中,线性负荷会使流经其位置的电流产生有固定比例关系的电流和电压,非线性负荷则不会在电流和电压之间建立线性关系。根据负荷的这一特点,定位谐波源,当不平衡负荷参数与时间变量之间呈现非线性关系,存在谐波源;当不平衡负荷参数与时间变量之间呈现线性关系,不存在谐波源。
考虑到配电网中负荷多数呈现出感性,在定位谐波源时,使用电阻和电感的串联来表示负荷模型。如图1所示。

图1 负荷等值的电路模型
图中PCC表示公共连接点,ic(t)表示PCC处的电流量测瞬时值,E˙表示供电侧等效电压源,uc(t)表示PCC处的电压量测瞬时值,L表示阻抗,根据KVL定理得到以下公式:
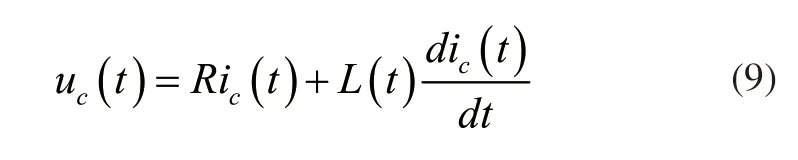
式(9)中t表示时间。假设存在t1和t2表示相邻的两个点,默认电阻R和电容L是固定的,整理式(9),得到:
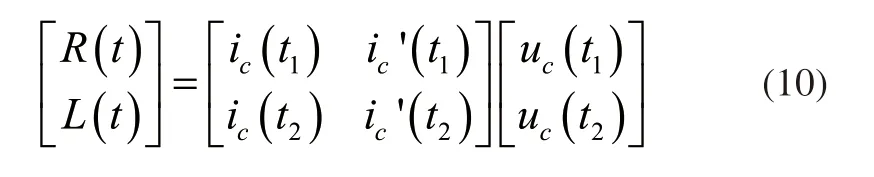
依据式(10),得到R和L各个点的瞬时值,确定谐波源的位置,考虑同一位置上可能存在多个谐波源,每个谐波源产生的电流可能相互抵消,为了更准确的掌握谐波源位置信息,实现谐波的有效检测,划分多谐波源责任,以此确定真实有效的检测目标。
1.3 划分多谐波源责任
假设配电网中某一位置存在多个谐波源负荷,在多个谐波负荷的作用下,PCC处的电流和电压产生波形畸变,其变形的程度与负荷的大小息息相关。在多谐波源责任划分中,将各个谐波源负荷等效为恒定谐波电流源。
以m次谐波为例,PCC点处的电压表示为:


1.4 检测PMU数据谐波
在检测PMU数据谐波中,根据PMU数据的量测量和量测量估计值计算量测残差相量,进而得到残差协方差矩阵,使用该矩阵检测PMU数据谐波。残差相量的计算是为了判断PMU数据中是否存在谐波,当PMU数据中存在谐波,但是计算的残差协方差恒等于0时,谐波是无法检测的,因此在谐波检测时要注意残差协方差等于0的问题。PMU数据残差相量计算公式如下:
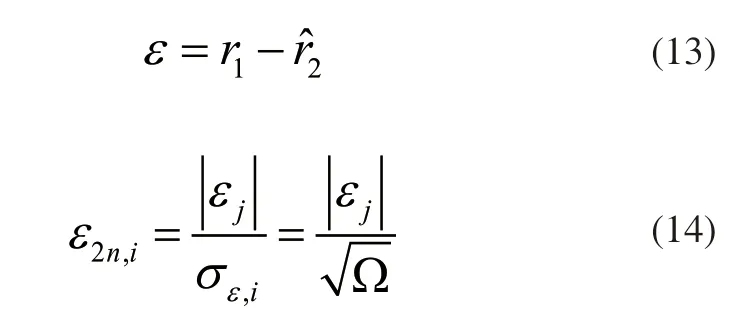
式中r1表示PMU数据量测量实际值,表示PMU数据量测量估计值,ε表示PMU量测残差相量,σε,i表示标准化偏差值,ε2n,i表示标准残差,Ω表示协方差矩阵。计算公式如下:

式中T表示旋转矩阵,v表示谐波状态估计的协方差矩阵,O表示量测雅可比矩阵,J表示PMU数据增益矩阵。将式(16)代入到式(15)中,就可以实现对PMU数据中的谐波进行检测。至此,基于不平衡负荷预测的配电网PMU数据谐波检测方法设计完成。
2 基于不平衡负荷预测的配电网PMU数据谐波方法实验研究
2.1 建立配电网仿真模型
对基于不平衡负荷预测的配电网PMU数据谐波方法研究时,以IEEE13节点作为实验案例,依据该节点系统的接线情况,使用MATLAB软件仿真出配电系统。IEEE13节点系统的接线情况如图2所示。
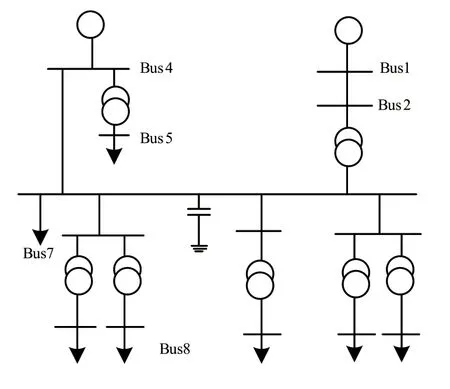
图2 IEEE13节点系统接线示意图
在仿真时,设置系统的基准容量为10000kVA,供电电压为69kV,采用AC/DC三相六脉动整流装置作为谐波源,以恒定的电压源代替原系统中的发电机,通过系统内的额定电压以及常数值的有功功率、无功功率来等效负荷,以谐波电流源替代谐波源负荷。
在仿真模型构建完成后,向节点注入PMU量测量,包括电压幅值和相角。具体量测配置内容如表1所示。

表1 PMU量测配置表
表1中量测类型I是节点电压幅值,类型II是节点电压相角,类型III是支路电流幅值,类型IV是支路电流相角。在PMU数据中存在一个非冗余的关键量测量,如果在实验中缺少这一关键量测量,将导致整个检测的失败,实验难以进行下去。因此在实验前,使用残差灵敏度矩阵识别关键量测量。公式如下:

式中χ表示状态向量,R-1表示量测数据相对状态向量的非线性函数,W和WT分别表示非线性指数和非线性指数的转置。在保证配电网PMU数据中包含关键量测量的情况下,进行后续实验。
考虑到常规的一些谐波检测方法存在的谐波状态估计不足的问题,在仿真模型建立完整后,将基于希尔伯特变换的谐波检测方法和基于二阶广义积分器的谐波检测方法作为实验的参考项,设计两组对比实验,分别是谐波源定位实验和谐波检测误差实验,在实验结束后,依据实验结果对比分析各个谐波检测方法的检测水平。
2.2 谐波源定位实验分析
通过MATLAB软件,在构建的配电网节点系统中模拟出谐波源,默认电感、电容同时存在,由电阻参数的变换模拟节点上负荷中的谐波源。在节点系统中选择存在负荷的支路作为实验点,使用不同的谐波检测方法检测目标,统计5次谐波和10次谐波的节点阻抗参数。实验结果如表2所示。
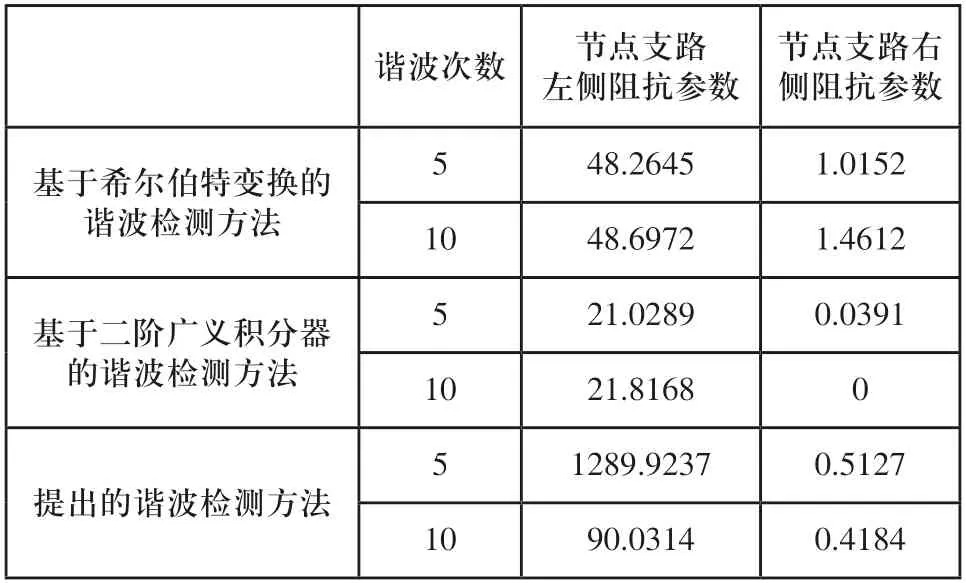
表2 不同谐波检测方法谐波源定位实验结果
由表2中数据分布情况可知,节点上的阻抗参数各不相同,基于希尔伯特变换的谐波检测方法和基于二阶广义积分器的谐波检测方法在不同谐波次数下节点上的阻抗参数没有明显的差异,说明在实验准备的节点中没有定位到谐波源,相比之下,设计的基于不平衡负荷预测的谐波检测方法实验结果中,节点阻抗参数具有明显的差异,说明节点中包含谐波源,并被该检测方法定位到。
2.3 谐波检测误差实验结果与分析
运行建立的仿真模型,得到各个节点的谐波电压幅值和相位,分析谐波电压情况可知,仿真出的配电网模型中主要谐波次数为5次和10次,10次以上谐波含有率比较低,从整体的谐波分布上可以看出,仿真的配电网模型符合谐波污染情况,能够满足实验要求。
在谐波检测误差实验前,将相量量测换成幅值量测,以PMU量测配置数据作为依据,使用不同的谐波检测配电网PMU数据谐波。获得的实验结果如图3所示。
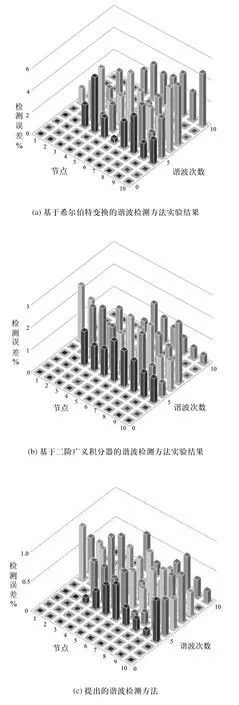
图3 不同谐波检测方法检测误差实验结果
从图3分析可知,使用提出的谐波检测方法检测PMU数据谐波后,检测结果误差都很小,幅值误差不到1%,完全符合检测要求。而其他两组检测误差实验结果中,随着谐波次数的增加,误差增加明显,远远高于2%,整体误差变化也比较大。说明提出的配电网PMU数据谐波检测方法不仅避免了谐波源定位异常对检测精度的影响,而且减轻了谐波次数增加对检测效果的作用。结合谐波源定位实验结果可知,提出的基于不平衡负荷预测的配电网PMU数据谐波检测方法检测精度高、谐波源定位准确,该方法优于常规的谐波检测方法。
3 结语
在配电网的研究工作中,为了保障电网的正常运行和电能的正常供应,对整个配电网和电力设备中的谐波进行检测,明确谐波的分布情况,进而为配电网的谐波治理提供更好的技术支持。本文以配电网PMU数据谐波检测作为研究重点,在翻阅了大量参考文献和资料后,设计基于不平衡负荷预测的配电网PMU数据谐波检测方法,在谐波检测方法设计完成后,以两种常见的谐波检测方法作为参考,设计多组对比实验,通过谐波源定位和谐波检测误差两组实验,证明了设计的谐波检测方法具有定位准确、高精度的优点,能够为配电网的正常运行提供一定保障。虽然,本文研究内容已经非常完善,在技术上取得了一定的进展,但是由于技术更新迭代,随着技术的发展PMU数据谐波检测方法需要不断更新,因此,在未来研究中,利用不断更新的高新技术不断优化检测方法,进一步完善配电网PMU数据谐波检测方法的各项功能。

