真正培养少数民族生的数学兴趣

史忠学

(甘肃省酒泉中学 735000)

甘肃省酒泉中学地处少数民族多杂居的边塞地区，自古以来有西出阳关等佳句，因此我校应责无旁贷地承担起培养我市少数民族学生的责任.

多年以前，我校招收有专门的少数民族班，教学按他们的实际情况实施方案，这样针对性强，而且好处理各种偶然性或必然性的矛盾，但现在各自治县(州)都有了完备的教学设施和师资，所以我校撤销了专门的民族班，在每个教学班里插进专收的二到三名少数民族生，有蒙古族，哈萨克族，藏族，裕固族，回族，土家族，东乡族等.这些学生相对其他学生来说文化课底子薄，差距大，行为习惯也缺乏培养.怎么样培养他们的数学学习兴趣，怎么样提高他们的数学基本技能和基础知识，是对少数民族生教学的关键所在.

根据多年来一线数学教育的实际，我将通过具体的一例说明.人民教育出版社出版的高中数学选修4-4《坐标系与参数方程》第33页例3.

例题如图1，O是直角坐标原点，A,B是抛物线y2=2px(p>0)上的两动点，且OA⊥OB,OM⊥AB并与AB相交于点M,求点M的轨迹方程.

课本旨在应用参数方程解决问题，具体如下:

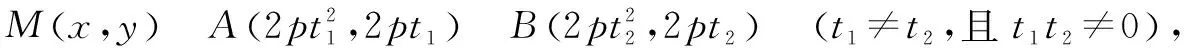
即(2pt1t2)2+(2p)2t1t2=0化简为t1t2=-1

①

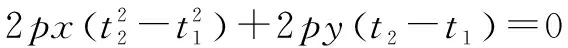
②

化简为y(t1+t2)-2pt1t2-x=0

③

即：x2+y2-2px=0(x≠0)

其标准方程为(x-p)2+y2=p2(x≠0)

分析小结此题思路有三段:

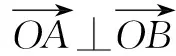
在实际教学中发现参数方程太深刻了，少数民族生难以融会贯通，相对来说普通方程对于他们来说稍微简单，所以我们教学中必须渗入这一点，而且其他基础薄弱的学生也由此获利.

以下给出几种普通方程解法:

联立得y1y2=-4p2

④

即：(x，y)·(x2-x1，y2-y1)=0

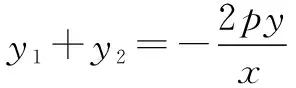
⑤

即：(x-x1)(y-y2)-(x-x2)(y-y1)=0

化简为：2px-y(y1+y2)+y1y2=0

⑥

然后把④⑤代入⑥化简得：

x2+y2-2px=0(x≠0)

所以标准方程为(x-p)2+y2=p2(x≠0)

分析小结此解法沿用了课本解法，只是用普通方程和直角坐标，对于普通学生来说好理解好运算，很明显运算过程简单.

解法二设M(xM，yM)，A(x1，y1)，B(x2，y2)

联立y2=2px得y2+2pky-2p(xM+kyM)=0

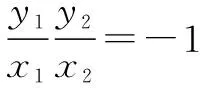
联立得y1y2=-4p2,所以得-2p(xM+kyM)=-4p2联立yM=kxM

分析小结此解法引用了OM：y=kx，用参数k联立普通方程，是所有学生的第一选择，好理解好运算，思维过程自然，运算过程简单.

分析小结此解法引用了OA：y=kx，用参数k联立普通方程，和解法二相似，是所有学生的不二选择，好理解好运算，思维过程自然，运算过程简单.

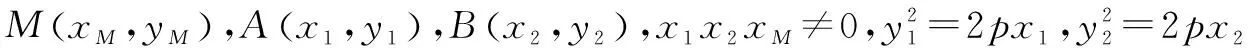
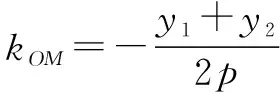
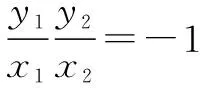
联立得y1y2=-4p2

即x2+y2-2px=0(x≠0)

其标准方程为(x-p)2+y2=p2(x≠0)

分析小结此解法用了圆锥曲线常用的方法——点差法，也是基本方法.

总结此例题除了课本给出的参数方程方法外，我又给出四种解法，而且四种解法都是普通方程和普通的直角坐标，学生容易理解，运算简单， 对于少数民族生因为环境条件所限，基础知识薄弱基本方法缺失，所以在高中数学教学中用最基本的方法和最基础的知识做为出发点，逐渐提高他们的学识和兴趣，而实际上我们也是从少数民族生的实际出发，这也得到了良好的效果，这也是探索到的关于少数民族学生的行之有效的教学之路.