例谈高中数学建模教学

蔡于兵

(江苏省泰兴中学 225400)

数学模型是基于对问题本质的理解，通过概括与抽象，运用数学语言描述的一种数学结构.高中数学涉及很多的模型，其中函数模型、概率模型、数列模型在测试中的出现频率较高.为使学生掌握并灵活应用这些模型，有必要进行针对性的讲解.

一、函数模型的教学

为使学生能够从实际的情境中抽象出对应的函数模型，应注重为学生深入的讲解函数模型的建立步骤、技巧，尤其通过函数模型的求解，使其掌握函数模型的求解思路.一般情况下，构建函数模型后往往运用函数性质求出最终的结果.

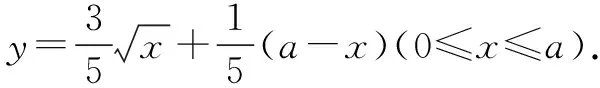
二、概率模型的教学

建立概率模型应通过审题明确问题所述的概率类型.通过回顾对应概率类型的计算公式，构建对应的模型.当然在构建概率模型时应注重善于从问题的反面出发，以简化解题步骤，提高解题效率.

(2)X=2，3，4，则X的分布列为：

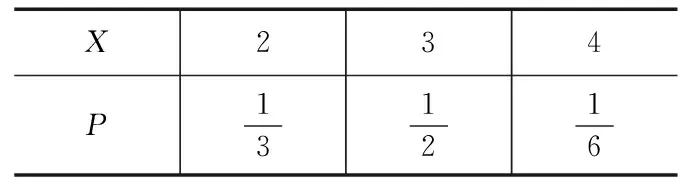
X234P131216

三、数列模型的教学

构建数列模型时往往有明确的关键词，如以后每年比上一年多(少)时则需要构建等差数列模型.如以后每年是上一年的多少倍(百分之几)则需要构建等比数列模型.然后根据题意运用等差、等比数列的相关公式求解，完成题目的作答.

例3甲、乙两个企业向签约10年的员工提供了两种均为税后的工资计算方式.甲公司第一年提供10万元的年薪，而后每年上涨20%；乙公司第一年提供20万元的年薪，而后每年上涨5%；若仅考虑收入水平，你会选择哪个公司，并说明理由.已知1.210≈6.19，1.0510≈1.63.

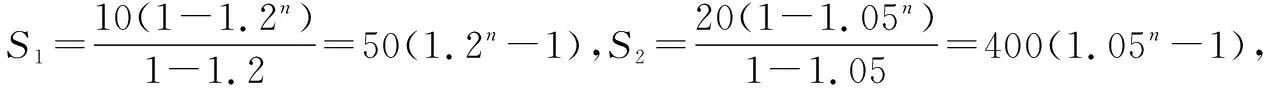
在数列模型构建时，教师需要加强课堂引导，让学生认真审题，分析题目意思，保证模型建构的准确性.在利用数列模型解题时，需要让学生思考所学习的等差和等比数列知识，全面理解题目内容，构建正确的数学模型，完成问题的分析和求解.

四、不等式模型的教学

在高中数学中，不等式是重要的基础知识，其题目类型较为复杂多变，而且不少题目和日常生活有关.在实际的不等式解题中，需要学生构建不等式模型，利用均值不等式知识完成解题.对于高中学生来说，部分学生缺乏建模意识和能力，无法完成题目情境向数学问题的转化，使得学生解题存在一定的难度.作为高中数学教师，应当以具体题目作为基础，让学生完成不等式模型构建，掌握不等式模型构建方式，提高学生不等式模型构建能力.

例4某货船在甲乙两点运送货物，货船最大速度是35km/h，甲乙两地之间的距离是500km.货船每小时航行成本包括燃料以及其他费用，燃料费用和速度平方成正比，系数是0.6，其余费用是960元每小时.(1)把全程运输成本y(元)表示为速度x的函数.(2)货船航行以多大速度，全程的运输成本最少？

因此，通过此题目的讲解，让学生可以更加全面的了解不等式模型解题策略，仅仅正确写出表达式是不够的，还需要去对定义域进行分析，保证最终计算结果的准确性.在此题解答中，当y取最小值时，x的取值并不在定义域的范围内，因此，不能够直接使用均值不等式进行求解.在高中数学解题中，教师应当避免学生的定势思维，引导学生灵活利用模型解题，保证解题效率和准确性.

高中数学建模教学过程中，不仅要为学生讲解具体的例题，更要注重在课堂上预留一定的时间鼓励学生反思与交流，使其把握不同数学模型特点，掌握数学建模的相关细节.同时，要求学生在课下及时开展相关的专题训练活动，积累相关的数学建模技巧，实现数学建模水平的进一步提升.