平面几何一题多解问题的探究
朱井龙
(上海市民办尚德实验学校 201315)
一、一题多解的价值
如果教师在平面几何教学中,注意挖掘和使用一题多解问题,除了可以强化学生的基础知识体系外,更重要的是能够发散学生的思维,提升学生的数学素养.而且在学生合作探究一题多解问题时,还可以发展他们的合作意识,提升他们的团队合作能力.下面这道平面几何问题是典型的一题多解问题,是平面几何教学中难得的好例题.
二、例题展示
例如图1,已知:BM=MC,∠BAM=∠MDC,求证:AB=CD.
分析这道题目中的已知条件并不复杂,图形结构也比较简单.但是,此题具有多种解法,每一种解法都针对了不同的知识体系.下面将从不同的角度,以不同方法去探究此题的解法.

三、解法分析
方法1利用中位线,构造两个等腰三角形,证明两线段相等.
辅助线:如图2,延长BA交CD于G,取BG中点F,联结MF.
易得MF=AF=AG=DG,所以AB=3AF,CG=2MF=2DG,CD=3DG=3AF,所以AB=CD.
方法2利用中位线,构造两个等腰三角形,由部分相等证明整体相等
辅助线:如图3,延长BA至E使AE=AB,联结CE,AE与CD交于F,易证AM∥CE,得AF=DF,CF=EF,所以AE=CD,从而证得AB=CD.
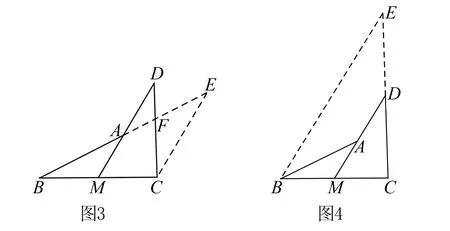
方法3利用中位线,构造等腰梯形,通过两腰相等证明两线段相等
辅助线:如图4,延长CD至E使DE=CD,联结BE,因为D、M分别是线段CE、CB的中点,所以DM∥BE,得梯形ADEB,又易证∠E=∠EBA,得等腰梯形ADEB,所以AB=DE=CD.

方法4利用三角形中位线证明两线段相等

方法5由梅氏定理的证明的思想,构造平行线,利用比例线段证明线段相等
方法6构造平行线,利用角平分线性质证明线段相等


方法7构造平行线,利用角平分线性质证明线段相等
方法8利用三角形等高不等底,面积之比等于底边边长之比

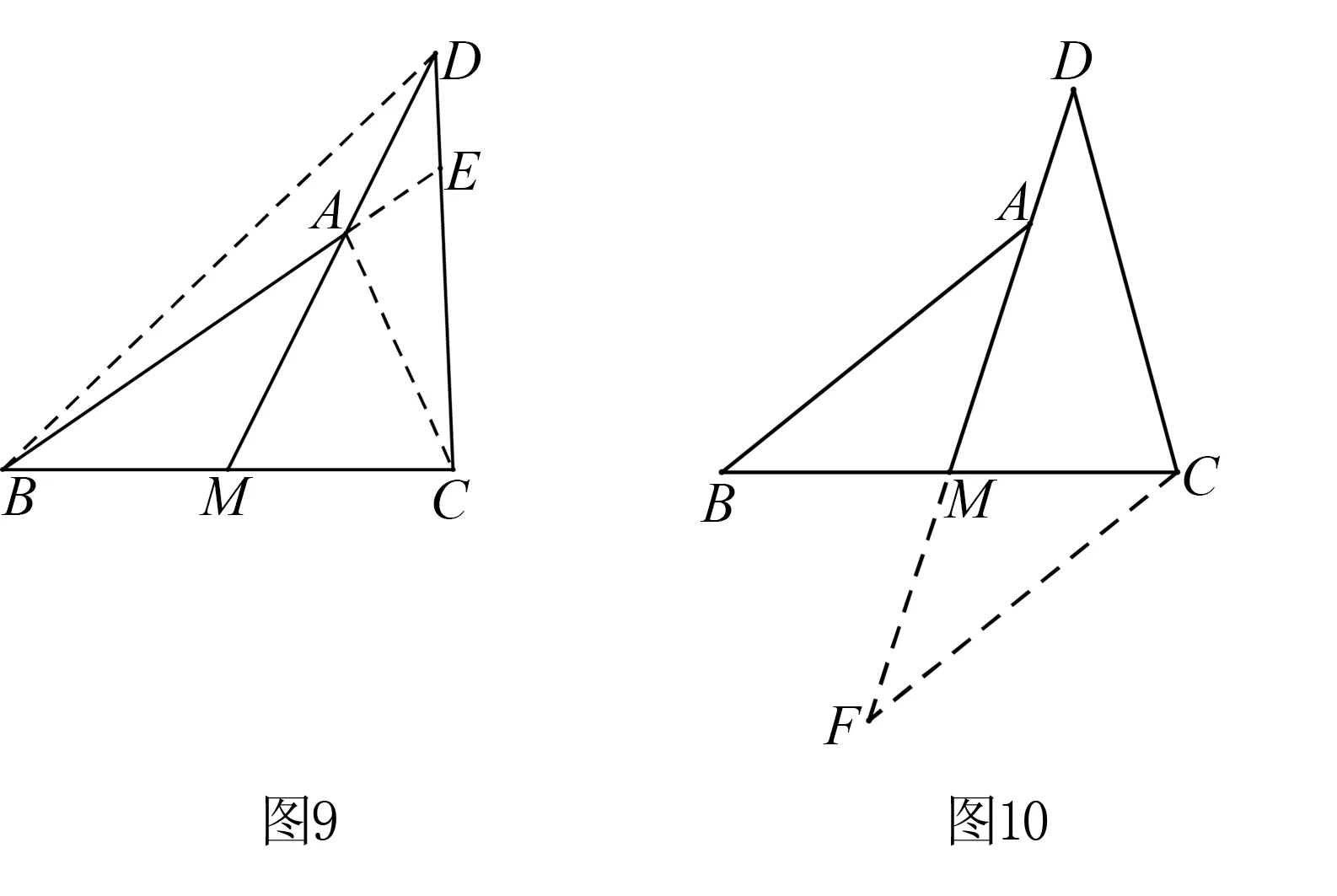
方法9构造全等及等腰三角形
辅助线:如图10,作CF∥AB,交AM延长线于点F,易得三角形ABM与三角形FMC全等,所以AB=CF, ∠BAM=∠F,因为∠BAM=∠D,所以∠F=∠D,所以CF=CD,所以AB=CD.
方法10构造全等及等腰三角形
辅助线:如图11,延长DM至点F,使MF=DM,联结BF,易得三角形BFM全等于三角形DMC,可得CD=BF,∠F=∠D,因为∠BAM=∠D,所以∠F=∠BAM,所以AB=BF,所以AB=CD.

方法11构造等腰三角形
辅助线:如图12,在边DM上取点F,使CF=CM,则CF=BM,∠MFC=∠FMC,所以∠DFC=∠FMB,因为∠D=∠MAB,所以三角形DFC与三角形ABM全等(AAS),所以AB=CD.
方法12利用中点构造全等三角形

辅助线:如图13,作CE垂直DM于点E,BF垂直DM于F,垂足分别是E,F,易得△FMB与△MCE全等,所以BF=CE,因为∠F=∠DEC=90°,∠D=∠BAM,所以△ABF与△DCE全等,所以AB=CD.
方法13利用正弦定理证明两线段相等

四、总结
教师可以在平时的教学中注意积累,打造一题多解的教学资源库.在教学实践中,不断地应用一题多解问题,将一个题目的内在价值充分地发挥出来,而不是让学生一味地重复练习.将平面几何内容的趣味性、学科价值等充分地发挥起来,为促进学生的数学素养发展作贡献.

