轮换矩阵可逆性的判定及其逆的计算

冯福存

(宁夏师范学院 数学与计算机科学学院，宁夏 固原 756099)

自1885年T.Muir提出了轮换矩阵的概念后，众多数学工作者对其进行了大量研究，轮换矩阵的应用广泛，涉及众多现代科学和工程领域，如编码理论[1]、密码学[2]、数字图像识别[3]、最优化等领域.文献[4]给出有限域Fq上n阶轮换矩阵的特征多项式和极小多项式的表达式,文献[5]利用特征值给出了一类特殊循环矩阵的判别及其对角化方法.矩阵求逆是矩阵代数中的一个重要运算，矩阵可逆的判定有相应的等价命题，但逆矩阵的获得却困难较多.本文在文献[6]的研究基础上，利用特征值和矩阵行列式的关系及多项式理论的相关知识给出了轮换矩阵可逆的两个等价命题，并给出了轮换矩阵逆矩阵的计算方法.为了叙述方便，记F[x]表示数域F上的一元多项式全体组成的集合，Pn×n为数域P上全体n阶方阵的集合，本文所提矩阵若无特殊说明，均指n阶方阵.

1 预备知识

定义1 若A∈Cn×n有如下形式

称A为轮换矩阵.因为轮换矩阵由首行元素决定，可记为A=circ(a0,a1,…,an-1).

定义2 若T∈Cn×n有如下形式

称T为基本轮换矩阵.

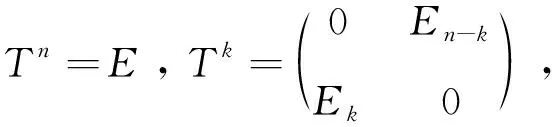
引理1[7]设f(x),g(x)∈F[x]，则f(x)与g(x)互素的充分必要条件是存在u(x),v(x)∈F[x]使得

u(x)f(x)+v(x)g(x)=1.

引理2[8]多项式f(x)无重因式当且仅当(f(x)，f′(x))=1.

引理3[9]若方阵A的特征值是λ，则矩阵多项式φ(A)的特征值是φ(λ).

引理4设f1(x),f2(x),g(x)∈F[x]，若(f1(x),g(x))=1，(f2(x),g(x))=1，则(f1(x)f2(x),g(x))=1.

证明因为(f1(x),g(x))=1，(f2(x),g(x))=1，由引理1可知存在ui(x),vi(x)∈F[x],(i=1,2)，使得

u1(x)f1(x)+v1(x)g(x)=1，

(1)

u2(x)f2(x)+v2(x)g(x)=1.

(2)

(1)，(2)两式相乘得

(u1(x)u2(x))f1(x)f2(x)+(u1(x)v2(x)f1(x)+v1(x)u2(x)f2(x)+v2(x)v2(x)g(x))g(x)=1，

所以(f1(x)f2(x),g(x))=1.

2 轮换矩阵的性质及其拓广

性质1 若A,B是轮换矩阵，则AT和λ1A+λ2B也是轮换矩阵.

证明由定义1知，显然.

性质2 基本轮换矩阵T是可逆的，其特征值是n个互不相同的n次单位根.

性质3[10]轮换矩阵的逆矩阵仍是轮换矩阵.

定理1T是基本轮换矩阵，则矩阵C为轮换矩阵的充分必要条件是

证明若C是轮换矩阵，不妨设C=circ(c0,c1,…,cn-1)，则

由定义2可知

(3)

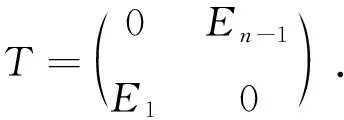
性质4 若A,B是轮换矩阵，则AB、BA均是轮换矩阵，且AB=BA.

证明设A=circ(a0,a1,…,an -1)，B=circ(b0,b1,…,bn -1)，T是基本轮换矩阵，由定理1可得

(4)

由基本轮换矩阵T的运算性质，将(4)式中T的各次幂的系数合并后记为dk(k=0,1,…n-1)，则

故AB、BA均是轮换矩阵.

若A是轮换矩阵，由性质3得A可逆时A*是轮换矩阵.由性质4得Ak是轮换矩阵.

3 轮换矩阵可逆性的判定

矩阵C是否可逆，可通过其行列式的值|C|判定，若C=circ(c0,c1,…,cn -1)，根据轮换矩阵的构成特征，由行列式运算性质可得

(5)

其中，Δ是第一列元素全为1的n阶行列式.

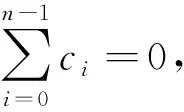
定义3 给定轮换矩阵C=circ(c0,c1,…,cn -1)，称φ(x)=c0+c1x+c2x2+…+cn -1xn -1为轮换矩阵C的伴随多项式.

定理3T是基本轮换矩阵，其特征值为λk(k=1,2,…,n)，轮换矩阵C=circ(c0,c1,…,cn -1)可逆的充要条件是φ(λk)≠0(k=1,2,…n).

证明由定理1可知(3)式成立，利用定义3得C=φ(T).由引理3可知C的特征值为φ(λk)(k=1,2,…,n).而矩阵C可逆的充要条件是|C|≠0.利用行列式与特征值的关系可得

即C可逆的充要条件是φ(λk)≠0(k=1,2,…,n)，故命题成立.

定理3虽然给出了轮换矩阵可逆的充要条件，但若n较大时，具体实施的过程中计算量太大，若利用多项式理论，进一步探索可得基本轮换矩阵的特征值均不是可逆轮换矩阵的伴随多项式的根，由此可得以下定理.

定理4 轮换矩阵C=circ(c0,c1,…,cn-1)可逆的充要条件是(φ(x),xn-1)=1.其中φ(x)是C的伴随多项式.

证明设基本轮换矩阵T的特征值为λk(k=1,2,…,n)，由性质2可知λk是多项式xn-1的根，轮换矩阵C=circ(c0,c1,…,cn-1)的伴随多项式为φ(x)，由定理3可知C可逆的充要条件是φ(λk)≠0(k=1,2,…,n)，即

(φ(x)，x-λk)=1,(k=1,2,…,n)，

由引理4可知

(φ(x),xn-1)=1.

4 轮换矩阵逆的计算

通过前一部分的推导，文章给出了判定轮换矩阵可逆的方法，依据相应的方法可计算矩阵的逆.结合定理3和定理4，利用矩阵多项式的性质，可进一步给出计算可逆轮换矩阵的逆的简便方法,该方法比矩阵求逆的初等变换法或公式法快速、准确 .

给定轮换矩阵C=circ(c0,c1,…,cn-1)，其伴随多项式为φ(x)=c0+c1x+c2x2+…+cn-1xn-1，由定理4可知(φ(x),xn-1)=1.即存在u(x),v(x)∈F[x]，使得(6)式成立.

u(x)φ(x)+v(x)(xn-1)=1，

(6)

将(6)式化为基本轮换矩阵T的矩阵多项式可得

u(T)φ(T)+v(T)(Tn-E)=E.

由

φ(T)=C及Tn-E=0,

可得

C-1=u(T).

注将公式(6)中的u(x)各项按变量x升幂的次序书写，由定理1可知u(x)各项的系数即为C-1的首行元素.

由性质3和定义1可以给出轮换矩阵逆矩阵的另一种计算方法：给定轮换矩阵C=circ(c0,c1,…,cn-1)，若C可逆，则C-1也是轮换矩阵.由轮换矩阵的特征，只需计算C-1的第一行或第一列元素便可得到C-1.设C-1的第一列元素构成的向量为x，取b=(1,0,…,0)T，非齐次线性方程组Cx=b的解便是C-1的第一列，轮换后可得C-1.

即

Cx=b,

可得

其中，C1i(i=1,2,…,n)是C的第一行元素c0,c1,…,cn-1代数余子式.

5 应用举例

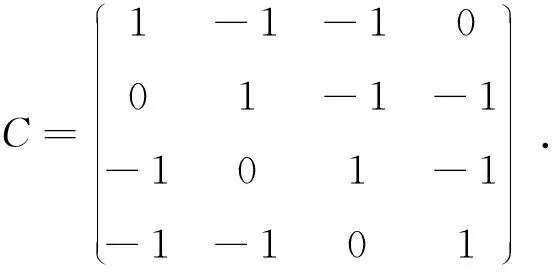
解由C是4阶轮换矩阵，可得C的伴随多项式为φ(x)=1-x-x2.4阶基本轮换矩阵T的特征值为

λ1=1，λ2=-1，λ3=i，λ4=-i,

故

φ(1)=-1，φ(-1)=1，φ(i)=2+i，φ(-i)=2-i.

由定理3可知

所以C可逆.

利用辗转相除法可得

x4-1=(-x2-x+1)(-x2+x-2)+(-3x+1)，

(7)

(8)

将(7)、(8)两式整理为(6)式得

得

C-1=u(T)

6 结论

本文论证了轮换矩阵经过相关运算(线性、乘积、转置、逆、伴随、幂)后仍是轮换矩阵，给出了判断轮换矩阵可逆的两个充要条件以及求轮换矩阵逆矩阵的计算方法.最后通过具体算例验证文中所提方法是较优的.