一类新的锥模型信赖域自适应算法
赵 绚,朱 帅
(1.运城师范高等专科学校 数学与计算机系,山西 运城 044000;2.山西大同大学 数学与统计学院,山西 大同 037009)
考虑无约束优化问题
(1)
其中,f:Rn→R二次连续可微.
求解此问题的大部分新算法是采用二次模型逼近f(x),但是对于一些非二次形态较强、曲率变化剧烈的函数,效果不是很理想.为此,Dnvidon[1]于1980年提出了锥模型,锥模型是二次模型的推广.Di和Sun[2]给出了锥模型信赖域子问题的最优性条件.文献[3]和[4]提出了基于锥模型的拟牛顿信赖域算法.
为了克服原目标函数在1-bTd>0的附近可能无界的情况,Ni[5]取消了对水平向量b的限制,对锥模型信赖域的子问题考虑了更为一般的情况,提出了一种新锥模型信赖域子问题
(2)
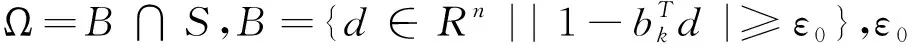


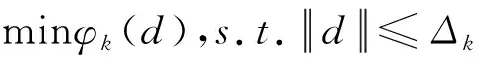
文献[6]中定义了关于ρk的R-函数以变化的速率来调节信赖域半径的大小,充分利用了ρk的信息,使信赖域半径的调节取决于问题本身,更具客观性.本文将R-函数以变化的速率来调节信赖域半径的大小的自适应和非单调技术[7-8]相结合,提出了一种基于锥模型的非单调自适应信赖域算法.
1 算法

定义1[6]Rμ(t)定义在(-∞,+∞)上,参数μ∈(0,1),Rμ(t)是一个R-函数,当且仅当它满足
(i)Rμ(t)在(-∞,+∞)上非减;
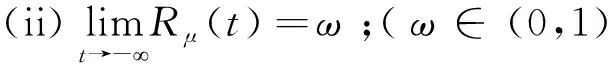
(iii)Rμ(t)≤1-γ1,(∀t<μ,γ1∈(0,1-ω)是一个常数);
(iv)Rμ(μ)=1+γ2,(γ2∈(0,+∞)是一个常数);

对于自动调节信赖域半径的R-函数,本文定义为[6]
算法1
step0 给定x0∈Rn,对称阵
step2 用折线法[9]求解子问题(2)得近似解dk.
step4 若ρk≥μ,令xk+1=xk+dk;否则取λk为
(3)
令xk+1=xk+λkdk.
step6 令k∶=k+1,更新bk[3]和Bk[3]
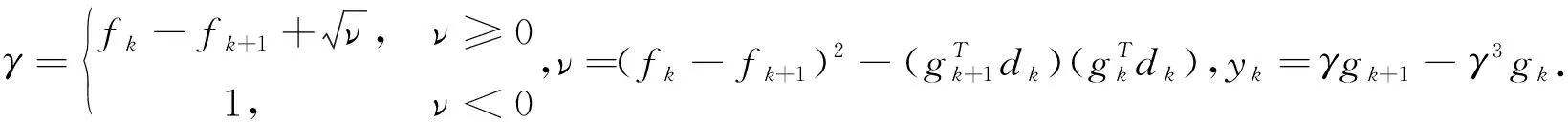
若ρk≥μ,令Mk+1=M;若μ<ρk<1,Mk+1=M+1.转step1.
2 算法的收敛性
2.1 本文假设
H1 水平集L(x0)={x|f(x)≤f(x0),x∈Rn}有界,且{xk}∈L(x0);
H2 数列{fk}有下界;
H3 ∇f(x)在Rn上一致连续;
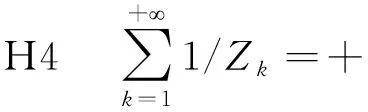

2.2 全局收敛性
引理1[8]若假设H2成立,则数列{fl(k)}非增且收敛.
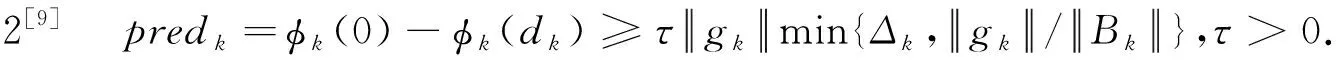

(4)

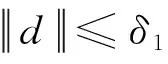
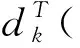
(5)
取ε=τδ(1-μ)/2,其中0<μ<1,τ>0,则
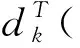
(6)
令
m=min{Δ1,Z1,ε0δ,ωδ,ωδZ1,τδω(1-μ)/2},
下面分两种情况证明(4)式.
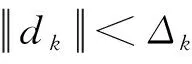
(7)
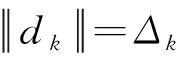
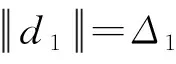
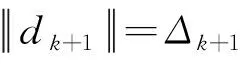
(8)
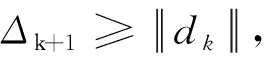
(9)
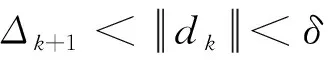
f(xk+dk)-fl(k)>-μpredk.
(10)
由(6)式知
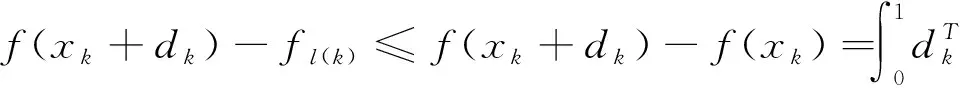
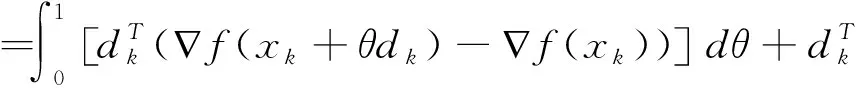
(11)


(12)
从而有
由(10)、(11)和(12)式有
(13)
而由引理2有
即
(14)
将(14)两边乘以(1-μ)加到(13),得到
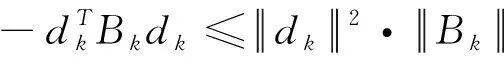
(15)
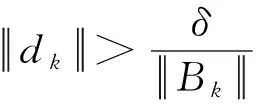
根据m的取法
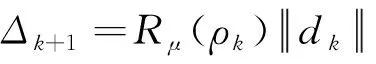
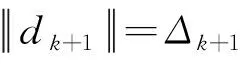

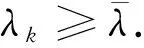
定理1 若假设H1-H5均成立,则由算法1产生的点列满足
(16)
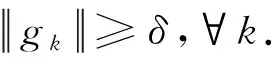
(17)
当k∈J时,
(18)
由(17)和(18)式知,存在常数ξ>0,对∀k,有fl(k)-fk+1≥ξ/Zk,从而
在上面不等式两边取最大值,有
fl(k)≥max{fk+1,fk+2,…fk+M+1}+ω/Zk+M+1,∀k,
又fl(k+M+1)≤max{fk+1,fk+2,…fk+M+1},∀k,从而有
fl(k)-fl(k+M+1)≥ω/Zk+M+1,∀k.
(19)
由引理1及(19)式得到
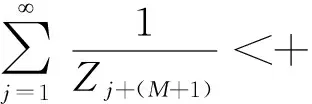
由上式及序列{Zk,k=0,1,2…}单调上升,可以得到
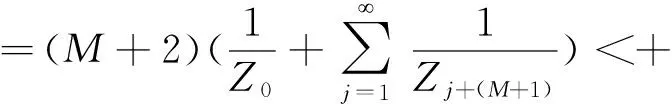
这与假设H4矛盾.证毕.
3 数值结果
本节数值试验选用三个标准测试函数如下
E1 Penalty-I function
这里α=10-5.
E2 Freudenstein-Rothfunction
f(x)=(-13+x1+((5-x2)x2-2)x2)2+(-29+x1+((x2+1)x2-14)x2)2.
E3 Rosenbrock function
在Matlab7.0环境下编制程序,参数设置如下
Δ0=1.5,μ=0.75,M=4,α=0.1,λ0=0.5,β=0.25,ε0=0.01,
B0=I,γ1=γ2=0.01,ω=0.1.

表1 算法1数值实验结果
数值结果表明,参数γ1和γ2的选取对算法1影响不大,从迭代次数和计算结果来看,该算法的计算效率比较高.表2的数值结果分析,在相同的终止条件下,采用相同的自适应调节方法,针对非二次形态较强的函数,文献[10]采用二次模型逼近原函数,结果显示算法1的迭代次数要远远小于文献[10]算法的迭代次数,计算结果也较为精确,大大减少了计算量.表3的数值结果分析,文献[11]采用锥模型逼近原函数,自适应技术仅利用函数的梯度信息进行调节,相比较本文算法1的自适应调节技术信息较少,数据显示算法1在迭代次数上要小于文献[11],说明新算法是稳定有效的.

表2 算法1和文献[10]数值实验结果比较

表3 算法1和文献[11]数值实验结果比较

