基于信息干预和治疗的时滞SIRS传染病模型的最优控制

李小妮

(陕西国际商贸学院 通识学院，陕西 西安 712046)

流行病的传播和暴发对人类的健康、社会发展等各方面造成巨大影响.及时有效的防控措施能在很大程度上降低流行病对社会的冲击，而研究流行病的传播规律可以为相关部门制定有效的防控政策提供理论依据[1].近年来许多学者利用数学工具对传染病传播规律进行了研究[2-5].在疾病暴发初期，由于药物治疗措施的缺乏，信息干预(消息传播、教育、隔离等措施)就变成一种及时且低成本的防控措施[4-6].Xiao[4]的研究表明信息干预可以降低流行病峰值，延缓疾病暴发.因此，在流行病的防控中,信息干预是一种不可或缺的控制措施.

另一方面，药物控制措施是一种更直接有效的控制措施.疫苗接种是最常用的防控措施之一，可以有效降低易感人群的发病率和感染人群的死亡率[7].因此，在消除传染病方面，疫苗接种等治疗措施是重要手段之一,可以最大限度地控制疾病的传播[8-9].

在流行病防控的过程中，过量的宣传报道和药物治疗不仅给群众心理和生活产生负面影响，也增加了流行病防治的成本.对相关部门来说，制定合适的宣传和疫苗接种策略也可以在很大程度上节约社会资源、降低人力物力成本.将控制策略在数学模型中作为决策变量建立最优控制模型，可以求得控制策略的最优使用量.因此，许多作者将治疗、疫苗接种等作为控制变量，建立并求解最优控制问题[10-12].例如，Kumar[12]将信息干预和治疗措施作为控制变量求解了最优控制问题.在流行病的传播过程中，时滞也是不可避免的因素之一.将时滞引入到数学模型中,可以使模型更加符合实际.因此，近年来有许多学者研究时滞流行病模型[13-14].流行病通常具有一定时间的潜伏期，这可以通过在模型中引入时滞来描述.

因此，本文将信息干预和治疗强度作为控制变量，来研究时滞SIRS传染病模型混合最优控制问题，从而在控制疾病暴发的前提下，得出最优的信息干预量和疫苗接种率.目前只有少量的文献研究时滞模型最优控制问题.所以对时滞模型来研究最优信息干预和治疗强度是很有必要的.

1 模型的建立

为了描述信息干预与疫苗接种对传染病的影响，文献[15]提出了如下带信息干预和疫苗接种的SIRS传染病模型

(1)

其中S,I,R,Z分别代表易感者、感染者、恢复者、信息密度且模型 (1)中所有参数都是非负的.模型(1)中的生物学意义为:b,μ,c,β,α,γ分别表示出生率、自然死亡率、因病死亡率、感染系数、恢复率、感染者的恢复率；p表示疫苗接种率(0≤p≤1)；φ是正函数其中φ(0)=1且φ′(I)≥0；m,u1,a,a1,a0分别表示信息干预率、信息强度、信息增长率、饱和常数和信息自然消亡率.

由于教育等信息干预措施和治疗措施对流行病的防控具有重要作用，将信息干预和治疗强度作为控制变量引入模型(1)，得到新的基于信息干预和疫苗接种的SIRS传染病最优控制模型

(2)

其中，u1(t)表示信息干预措施的强度，u2(t)为治疗措施的强度；α1,α2,α3为饱和常数.

本文的目标为寻找最优控制函数(u1(t),u2(t))，达到降低感染者数量.为此，定义最优目标函数：

其中，[0,T]代表加入控制策略之后整体时间区间，正常数Ai,Bi,Ci(i=1,2)为相应的权重值，使得目标函数J达到最优.

2 最优控制的存在性及其刻画

首先证明最优控制的存在性，然后通过构造Hamilton函数对最优控制问题进行求解，以达到设定的控制目标.

2.1 最优控制的存在性

最优控制的存在性是求解最优控制问题的基础，所以给出最优控制存在性的结果.

(3)

其中，u为凸紧集.

证明为证明最优控制的存在性，应用文献[16]的结果.在此最优问题中，目标函数(3)是凸函数，且最优控制变量(u1,u2)与控制状态变量非负.由控制集的定义可知，U为凸紧集.同时，最优系统是有界的.L(A1,A2,A3,u1,u2) 在U中是凸函数.存在常数C1,C2使得

2.2 最优控制的刻画

通过构建 Hamiton 函数，使用 Pontryagins 最大值原理解决系统(2)的最优控制问题.为方便起见，χ[a,b](t)表示区间[a,b]上的示性函数.下面给出最优控制问题的一阶必要条件.

(4)

其中，λi(T)=0(i=1,2,3).相应的最优控制为

(5)

其中

证明为了简便，令X=(S,I,R,Z)T,u(t)=(u1,u2)T且λ(t)=(λ1,λ2,λ3,λ4)T,χτ(t)=X(t-τ).Hamiton 函数为

(6)

(7)

于是由Hamiton 函数的表达式可得

(8)

化简方程(8)可得

由控制变量ui(t)(i=1,2)的有界性，可得方程(5)成立.

(iii)伴随方程为

将(6)代入上式得到

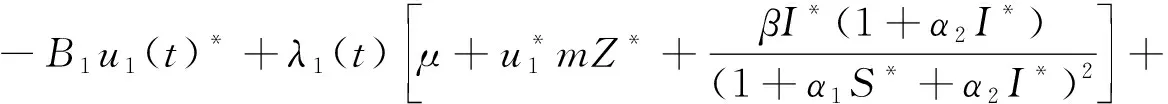
其中，λi(T)=0(i=1,2)为横截条件.证毕.

3 数值模拟

表1 最优控制实现算法

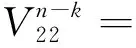
模型(2)的参数取值如下

T=200,Δ=0.01,τ=10,p=0.8,b=5,μ=0.03,β=0.04,α1=0.06,α2=0.04,

γ=0.045,m=0.43,c=0.11,α=0.37,α3=0.012,a=0.045,a1=0.15,a0=0.06.

权重为A1=0.5,A2=0.3,B1=3×10-4,B2=5×10-4,C1=200,C2=7×103.模型(2)的初始值为S(0)=10000,I(0)=100,R(0)=1,Z(0)=10.

数值模拟的结果如图1所示.图 1(a) 给出了无控制措施和有两种控制措施时感染群体的时间序列图，从图1中可以看出，在实施控制措施之后，I(t)的值大幅下降，在时间段40≤t≤60之间下降速度最快.由此可以断定，流行病暴发之后采取教育和治疗措施对疫情的防控具有重要意义.图1(b) 给出了两种控制措施u1和u2的取值.为了了解单一控制措施的作用，令u2=0和u1=0来考察u1和u2对感染人数的影响，其结果如图1(c) 所示.由图1可知，当只采用教育措施 (u1) 时，在初始时刻附近对感染人数I(t)几乎没有影响，但在后期可以让感染人数大幅下降.这可能是宣传教育对流行病控制的滞后作用造成的，虽然在流行病暴发的初期就会采取教育措施，但人们对疾病的认识和自身行为的改变需要较长时间，所以教育措施的作用在后期比较明显.对于仅采取治疗措施的情形，在初始时刻附近就出现感染人数下降的现象，在后期虽然感染者数量也在不断下降，但下降幅度较小，出现这种现象的原因是：治疗措施直接针对的是感染者，能快速显现其效果，但无法像教育措施那样切断感染源，所以在中后期治疗措施的效果不明显.综合以上结果可知，采取多种综合措施比采取单一控制措施对抑制流行病的暴发具有更明显的效果.

图1 最优状态和最优控制

4 结论

流行病的传播和暴发给人类健康造成极大的威胁，宣传教育和治疗是控制传播的重要措施.因此，本文研究了基于信息干预的SIRS传染病模型的最优控制，将信息干预和治疗措施作为控制变量，给出了最优控制存在的一阶必要条件.通过数值模拟验证了文中得到的理论结果，也揭示了信息干预和治疗措施对流行病具有不同的影响.相比于采取单一措施，同时采取两种措施对流行病的防控具有更好的效果.