量子控制非门核磁共振脉冲序列设计与验证

彭永刚

1.南京邮电大学 理学院 应用物理系，南京210003

2.江苏省新能源技术工程实验室，南京210003

核磁共振量子计算是利用已经研究了六十多年的非常完善的核磁共振技术所实现的量子计算方案。近十几年，核磁共振量子计算方案实验研究[1-6]快速发展，成为量子计算物理实现的候选方案之一。利用核磁共振实现量子算法，需要用到单量子位逻辑门操作和两量子位逻辑门操作，对于单量子位逻辑门操作需要一个微秒量级的射频脉冲磁场来实现，对于两量子位逻辑门操作，需要控制射频脉冲磁场与系统内部核自旋之间的相互作用（不加射频磁场脉冲）随时间演化的合理组合来实现。量子算法是由一序列基本幺正变换的乘积构成的，利用核磁共振技术实现量子算法就是把一序列基本幺正变换编译成现代超导核磁共振谱仪上能够直接执行的核磁共振脉冲序列。1995年，Barenco等人[7]已证明：任意一个量子算法可以写成两量子位量子控制非门和一位单量子位门的组合，因此，研究量子控制非门的核磁共振的物理实现，对研究量子算法的核磁共振物理实现具有重要意义。1999年，Price等人[8]提出用经典几何代数学的方法构造量子控制非门的核磁共振脉冲序列。2001年，Fung等人[9]提出用成对的伪纯态代替单个伪纯态的方法来设计核磁共振脉冲序列，实现量子控制非门。2018年，Gaikwad等人[10]提出量子过程层析成像的方法实现核磁共振量子控制非门。2018年，Jiang等人[11]提出零磁场核磁共振脉冲序列的方法实现量子控制非门。2020年Zeng等人[12]提出了验证核磁共振实现量子控制非门的方法。本文运用在核磁共振条件下单体和两体含时薛定谔方程[13-15]的近似求解方法，研究量子控制非门核磁共振物理实现脉冲序列的设计和脉冲序列参数取值。根据Suzuki乘积公式[16-18]，给出数值求解含时薛定谔方程的方法，用该方法对含时薛定谔方程进行数值计算，验证量子控制非门磁共振脉冲序列设计和参量取值的正确性。

1 量子控制非门核磁共振实现的脉冲序列

1.1 两量子位核磁共振量子处理器

1H、13C、14N、31P等原子的核自旋均为1/2，可作为量子比特使用。在一个分子中，如果有两个核自旋为1/2的原子，可作为一台两量子位的处理器[1，19]，在外加的均匀磁场和射频磁场中，这个自旋1/2两核自旋系统的哈密顿量[1，19]为：

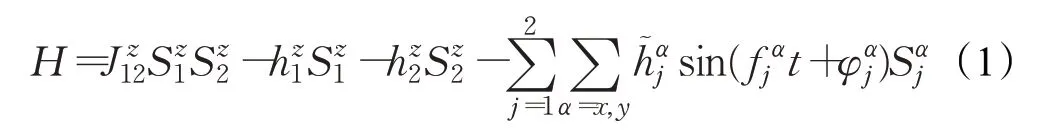
式中，表示第j核自旋沿α方向自旋算符，表示核自旋1和核自旋2之间相互作用的强度，表示作用在核自旋沿z轴方向的均匀磁场，表示作用在第j核自旋沿α方向的射频磁场表示作用在第j核自旋沿α方向射频磁场的频率和初相位。

1.2 单量子位逻辑门核磁共振实现

核自旋状态的波函数是一个二分量的列旋量，向上和向下的基矢量可表示为：

单个核自旋受到沿着z轴的均匀磁场和沿x轴的射频脉冲磁场作用，其状态随时间的演化，遵守单体含时薛定谔方程：

核自旋绕x轴转动，需要在y轴上施加射频脉冲磁场。核自旋绕x和y轴顺时针转动π/2的操作可表示为：

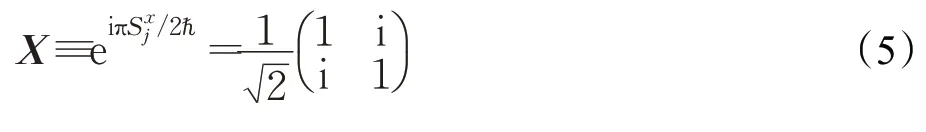
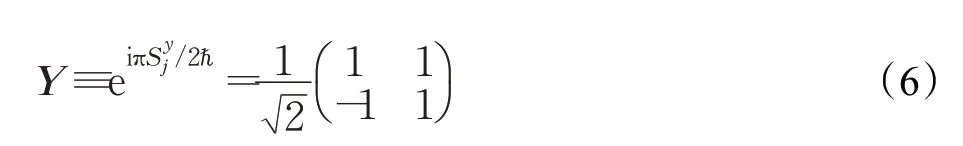
第j核自旋绕x轴和y轴逆时针转动π/2的操作表示为：

1.3 量子控制非门核磁共振脉冲序列设计

量子计算中两核自旋之间通过核自旋与核自旋的相互作用交换量子信息，核自旋1和核自旋2之间的相互作用受控相移门[20]为：

其中，c0=a0+a1，c1=a1-a0，c2=a2+a3，c3=a3-a2，由于量子控制非门的定义是当且仅当第一核自旋处于态时，才翻转第二核自旋的状态，这要求ϕ00=ϕ01，式（13）改写为：

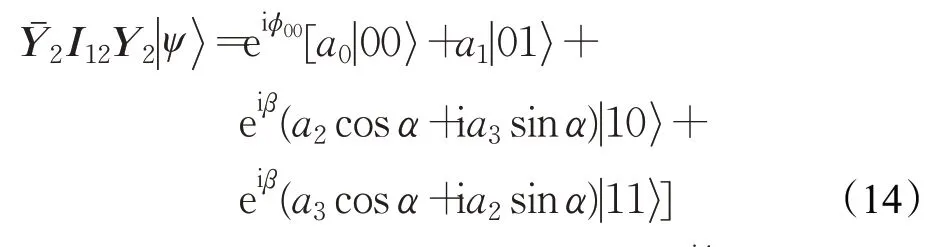
式中，β=α+ϕ11-ϕ00，α=(ϕ10-ϕ11)/2，eiϕ00是无关紧要的整体相位因子，根据伊辛模型：

执行受控相移门I12=e-iτH,则ϕ00=τ(J/4+h),ϕ01=ϕ10=-τJ/4，ϕ11=τ(J/4-h)，考虑到ϕ00=ϕ01，式（14）改写为：

τ表示量子处理器在没有外界射频磁场作用时，两量子位核自旋系统的状态在哈密顿量式（15）的支配下，随时间演化的时间间隔。

在伊辛模型式（15）中两个核自旋处于相同的静态磁场，但实际上两个核自旋处于不同的静态磁场，这个静态磁场为：

是通过系统随时间演化e-iτHNMR来实现，演化时间间隔为τJ=-π，由式（22）可知，实现量子控制非门的核磁共振脉冲序列不是唯一的。

1.4 核磁共振脉冲序列参数的取值

一种理想的情况。实际情况是使核自旋1发生共振的射频脉冲磁场不仅会改变核自旋1的状态，也会改变核自旋2的状态，要参数设定更准确，必须求解两体核自旋系统的含时薛定谔方程，考虑数值计算中的参数设定是采用参考文献[1]参数式（24），核自旋之间相互作用时间远小于射频脉冲作用持续时间，这时核自旋之间相互作用对核自旋在射频脉冲作用下随着时间演化的影响可以忽略不计，两体含时薛定谔方程为：

采用自然单位，令ℏ=1，这时两个核自旋处于一个静态磁场和一个射频正旋磁场中，这时选择在旋转参考系[13]中计算含时薛定谔方程，当射频磁场与核自旋1发生共振，即

其中，k2、n2是正整数，式（34）和式（35）无精确解，但在k1和k2很大，γ为有理数时，令γ=N/M，0>1，那么，k1=kMN2和k2=k NM2将使方程式（34）和式（35）产生足够精确解，相关物理量之间的关系由下式给出：

式（19）、式（22）和式（36）是量子控制非门脉冲序列参数取值的关系式，核自旋1和核自旋2绕x轴转动π/2的脉冲序列参数取值也有同样的关系式。在式（36）中，取k=1，M=4，N=1，再利用式（22），射频脉冲序列的操作时间τ以及等参数取值见表1，表1中各参数的单位为109πHz。在式（36）中，取k=1，M=4，N=1，再加上式（19）计算出实现量子控制非门核磁共振脉冲序列的单量子位逻辑门及受控相移门的执行时间τ，得到执行时间参数见表2，执行时间单位为4πns。当k=2、8、32时射频脉冲序列的操作时间τ以及等参数不予赘述。

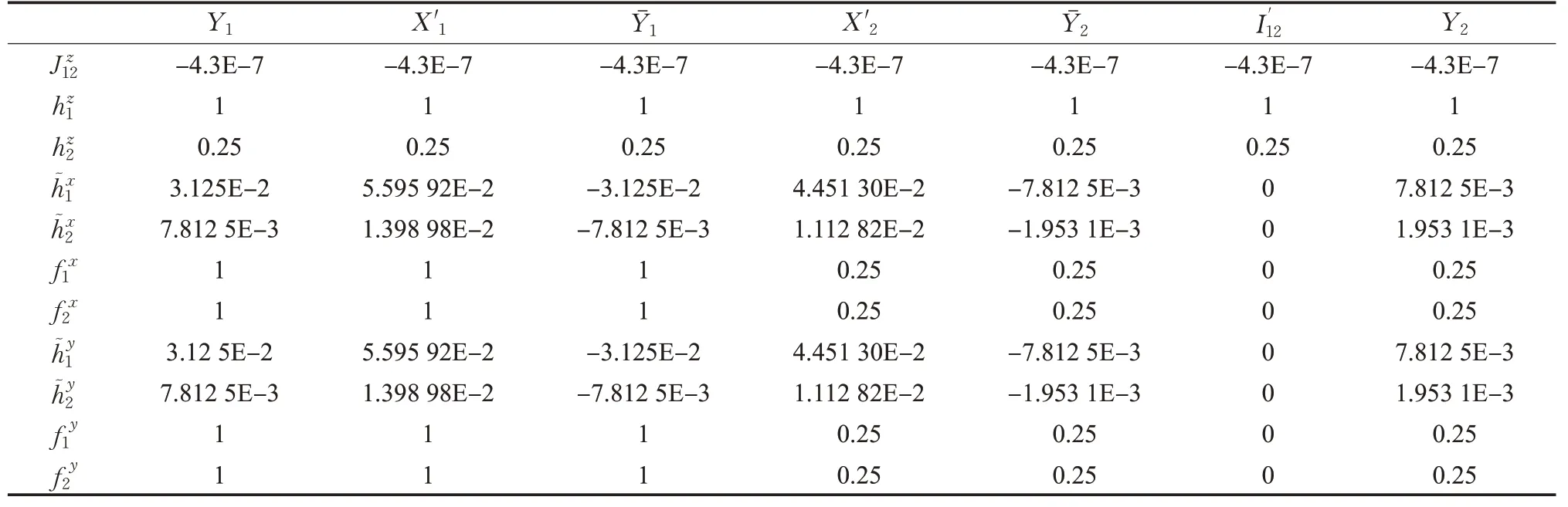
表1 k=1量子控制非门脉冲序列参数J和h取值Table 1 Parameter values of quantum controlled not gate pulse sequence J and h for k=1 109πHz

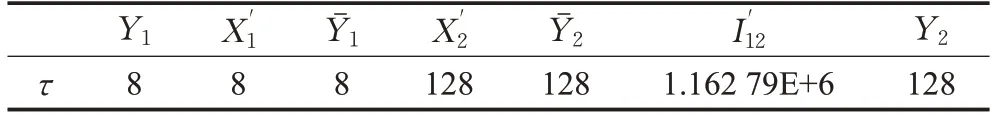
表2 k=1核磁共振脉冲序列参数执行时间τ取值Table 2 Parameter execution timeτof NMR pulse sequence for k=14πns

2 量子控制非门脉冲序列设计与参数取值正确性的验证

2.1 含时薛定谔方程的数值求解方法

为了验证上述量子控制非门核磁共振实现脉冲序列设计及参数取值的正确性，需对含时薛定谔方程进行数值求解。核自旋系统随时间的演化遵守含时薛定谔方程：

在特定的射频脉冲执行过程中参量J、h和h͂可看成是恒定的。显然上述构造U͂(δ)是幺正的，上述求解含时薛定谔方程的算法是无条件稳定[16-17]的。可以证明|U(δ)-U͂(δ)|≤cδ3，这意味着在二阶时间步长δ内算法是正确的，这种解法的结果和式（37）的含时薛定谔方程的精确解没有区别。

2.2 数值求解计算结果与讨论

在参数设定关系式（35）中取k=1时，实现量子控制非门核磁共振脉冲序列及控制相移门的执行时间τ、时间步长δ和时间步m数见表3。当k=2,8,32的执行时间、时间步长及时间步数不予赘述。

表3 k=1脉冲序列执行时间、时间步长和执行步数Table 3 Pulse sequence execution time，time step and number of execution steps for k=1 4πns

用上述数值求解含时薛定谔方程的方法编程计算得到：k=1,2,8,32时，量子控制非门作用于时，量子位1和量子位2的Q1、Q2随时间演化曲线如图1、图2、图3和图4所示。

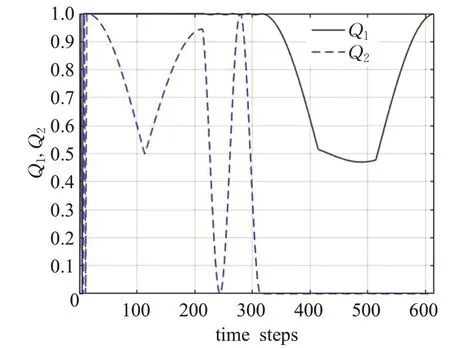
图1 k=1时，Q1和Q2时间步数演化Fig.1 Evolution of Q1 and Q2 for k=1

图2 k=2时，Q1和Q2随时间步数演化Fig.2 Evolution of Q1 and Q2 for k=2

在图1、图2、图3和图4中，纵坐标Q1表示第一量子位的核自旋z方向分量的期望值随时间演化，由实线表示，Q2表示第二量子位的核自旋z方向分量的期望值随时间演化，用短划线表示。横坐标表示时间步数，横坐标除相互作用受控相移门I′12外，执行一个基本操作的时间步数是100，图1、图2、图3和图4中Q1和Q2随时间演化曲线表明：（1）在两个核自旋之间相互作用时间远小于射频脉冲作用时间这个条件下，当2kN(M-N)>>1时，式（35）确实是式（33）和式（34）足够精确的近似解，上述两体含时薛定谔方程的近似求解方法是正确的。（2）本文的设计确实能使射频磁场对核自旋1作用时对核自旋2不起作用，射频磁场对核自旋2作用时对核自旋1不起作用，相互作用受控相移门I′12在时间步数300左右在核自旋1和核自旋2发生明显相互作用。（3）验证了上述量子控制非门核磁共振脉冲序列设计和参数取值的正确性。

图3 k=8时，Q1和Q2随时间步数演化Fig.3 Evolution of Q1 and Q2 for k=8

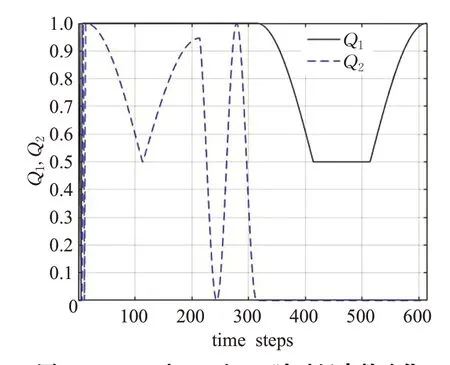
图4 k=32时，Q1和Q2随时间步数演化Fig.4 Evolution of Q1 and Q2 for k=32

3 结束语

通过单核自旋1/2系统绕x轴和y轴转动算符和两量子位相互作用受控相移门的组合，可设计量子控制非门核磁共振脉冲序列。当射频电磁场的频率与某一特定核自旋进动频率相同时，在两个核自旋之间相互作用时间远小于射频脉冲作用时间的条件下，这时两体含时薛定谔方程有足够精确近似解，由两体含时薛定谔方程的足够精确的近似解可推出量子控制非门核磁共振脉冲序列的参数取值之间的关系式。用Suzuki对称乘积公式对含时薛定谔方程进行数值求解计算，可验证量子控制非门核磁共振脉冲序列设计、参数取值的正确性和算法的稳定性。本文所使用的利用核磁共振实现量子控制非门的方法，即用单量子位转动门和两量子位之间相互作用受控相移门的组合也可用于构造其他量子逻辑门和量子算法。用Suzuki对称乘积公式数值求解含时薛定谔方程的方法也可用来验证其他量子逻辑门和量子算法设计的正确性。