基于超效率DEA和GIS的中国省际高校创新效率评价研究
冯亚枝 胡彦蓉 刘洪久
(1.浙江农林大学 信息工程学院, 浙江 杭州 311300;2.浙江省林业智能监测与信息技术研究重点实验室, 浙江 杭州 311300)
第二届“一带一路”国际合作高峰论坛开幕式指出,创新就是生产力,企业赖之以强,国家赖之以盛。党的十九大报告中明确强调“创新是引领发展的第一动力”,提高自主创新能力是我国发展战略的核心,是提高我国综合国力的关键,而高校的创新效率是我国整体创新能力的重要体现。因此,研究各省高校创新效率之间的差异,不仅可以为优化资源配置提供依据,还可以为提高高校创新效率和科研创新能力提供参考。
梳理国内外文献发现,现有对科研创新效率的研究主要分为以下三类:(1) 传统数据包络分析方法。如徐爱萍、万秋霞、王海宁等基于传统DEA分别对“一流”高校、财经类高校的科研效率进行评价研究[1-3];孔佳南等引入数据包络分析,对江西省2003年至2012年有色金属企业生态效率进行研究,发现技术水平的增长和规模效益的实现才是真正提高生态效率的根本途径[4]。(2) 采用Malmquist指数法、层次分析法(AHP)、随机前沿分析法、聚类分析和因子分析法、TOPSIS和熵权法、超效率DEA、模糊集定性比较分析(fsQCA)进行评价研究。如宗晓华采用超效率DEA方法对教育部直属高校2006—2015年间的科研效率及其影响因素进行分析[5];李彦华和马玲玲等采用Malmquist指数法测算了高校科研动态绩效[6-7];Valadkhani等运用聚类分析和因子分析对澳大利亚部分大学的研究绩效进行了分类评价[8];王宁采用TOPSIS、熵权法、因子分析对中国40所“一流大学”建设高校科研效率进行了评价[9];张卫国使用模糊集定性比较分析方法,对我国高校的科研生产率的提升路径进行研究,得出高校提高科研生产率的4条影响路径[10]。(3) 采用组合评价和人工智能方法对各高校科研效率进行评价研究,如SOM神经网络和两阶段DEA模型的组合方法等[11-16]。
国内外学者用不同的方法对科研效率进行了研究,这些评价方法大多采用传统DEA方法或超效率DEA方法与其他方法结合的模式进行评价,但缺乏从空间角度进行研究,超效率DEA方法和GIS结合的科研效率研究较少。因此,文章拟采用超效率DEA模型和GIS结合的模式对各省高校科研创新能力进行评价研究,并运用ArcGIS研究不同省份高校创新效率的空间分布特点,从而有助于发现提高各省高校创新能力的方法,为区域政府制定创新政策提供参考依据。
1 研究方法和指标体系建立
1.1 研究方法
(1) 传统DEA和超效率DEA。传统DEA又分为CCR模型和BCC模型,决策单元j记为DMUj,n个决策单元都具有可比较性,每个决策单元都有m种“输入”和s种“输出”,1≤j≤n;xij为第j个决策单元对第i种输入的投入量,xij>0;yrj为第j个决策单元对第r种输出的产出量,yrj>0;vi为对第i种输入的权重;vr为对第r种输出的一种度量,构成如下CCR模型:
BCC模型假设n个决策单元对应的输入输出数据分别为:xj(x1j,x2j,…,xmj)T,j=1,2,…,n,yj(y1j,y2j,…,ysj)T,j=1,2,…,n,其中,xj∈Em和yj∈Es,xj>0,yj>0,j=1,2,…,n,构成BCC模型为:
传统的DEA模型产生多个DEA评价单元,可以判断它们相对有效或者非有效,但是得出的相对有效DMU效率值都为1,却不能为它们的大小进行排序,评价单元间的关系难以区别,超效率DEA模型就用来解决这个问题:
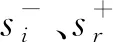
(2) 空间自相关分析。一般用来研究空间某点的观测值是否具有相关性以及空间集聚特征,又分为全局空间自相关和局部空间自相关两种类型。
全局空间自相关主要分析研究的区域是否存在空间正相关、负相关或者随机分布,Moran’s I指数表示空间邻接的区域属性值的相似程度,1表示空间数据间存在着强烈的正自相关性,-1表示空间数据间存在着强烈的负相关性,0表示空间数据是随机分布,不存在自相关性。全局Moran’s I指数的计算公式如下:
局部空间自相关可以看出局部地区空间集聚的水平,实质是将全局空间自相关性分解到更小的单元,考察地区附近的空间集聚情况,计算公式为:
(3) 空间半变异函数。该函数指数据点的半变异值与数据点间距离的函数,分析区域化变量空间异质性的重要工具之一,计算出不同空间滞后距离下的创新效率差异,统计创新效率差异与空间滞后距离的变化关系,因此本研究采用半变异函数分析省级高校创新效率空间异质性,半变异函数的计算公式为:
式中,h为样本之间的距离,N(h)为空间距离为h时样本点的对数,Z(χi)和Z(χi+h)分别为创新效率Z在空间位置χi和χi+h处的创新效率值。
1.2 指标体系的建立和数据来源
(1) 指标体系的建立。本研究在选取DMU的投入产出指标时,依据有效性与可行性、全面性与代表性、可比性与稳定性等原则,以及各省高校的特点,田水承等根据DEA原理[17],提出了对指标体系进行优化的原则和方法,据此本研究把影响科技创新的投入指标分为四个部分:科技人员、科技经费、研究与发展机构以及国际科技交流;产出指标包括:出版科技著作、发表学术论文数目、专利授权数。每个部分又分为二级指标,客观反映高校创新效率,具体见表1所示。
(2) 数据来源及评价指标的筛选。本研究以国内各省份高校作为样本来进行实证研究,从教育部科学技术司(http://www.moe.gov.cn/s78/A16/A16_tjdc/)选取《2013—2017年高等学校科技统计资料汇编》北京、上海、天津等25个省份高校的12项数据作为数据分析样本。

表1 创新效率评价指标体系
在所构建的指标体系中,文章采用鉴别力分析方法来评价指标的特征差异,如果评价指标在所有样本上的得分没有明显差异,那么就认为这个指标几乎不能区分各个研究对象的优劣。反之,则表明该指标具有较高的鉴别力,运用SPSS软件,以2013—2017年高等学校科技统计资料汇编中的原始数据为基础,在95%的置信区间内进行各个指标的显著性检验,得到单因素方差分析结果,结果表明,各省份不同指标的显著性检验P值都小于0.05,存在显著性的差异且具有鉴别力,从而验证表1所创建的指标体系合理性。
2 实证分析
2.1 基于传统DEA分析
建立相应的DEA模型,CCR模型综合效率表示该省份高校创新总效率,BCC表示该省份的纯技术效率,综合效率等于纯技术效率和规模效率的乘积。运用Deap 2.1软件对中国省际高校科技创新的综合效率、纯技术效率和规模效率进行计算,计算结果如表2所示。从表2中可看出:25个决策单元中,2013—2017年综合效率为无效的决策单元有12个,因为其规模和投入、产出不相匹配,需要增加规模或减少规模;综合效率有效的决策单元有13个,说明这些省份的高校创新效率是有效的。纯技术效率为1的省份有18个,若某省份纯技术效率为1但规模效率小于1,则表示对该省份本身的技术效率而言,没有投入需要减少、没有产出需要增加,满足这样的省份有5个,分别为:辽宁、黑龙江、湖北、湖南、重庆。规模报酬递减意味着产出比例的增加将小于投入比例的增加,反之,则意味着产出比例的增加大于投入比例的增加,规模报酬不变的省份有北京、河北、山西等13个;规模报酬呈现递减状态的省份有辽宁、安徽、湖北等6个;增加投入时要考虑投入产出的效益,可减少相应的投入从而达到最合适的规模,规模报酬递增的省份有天津、吉林、福建等6个省份,需增加相应的投入以达到最佳规模。
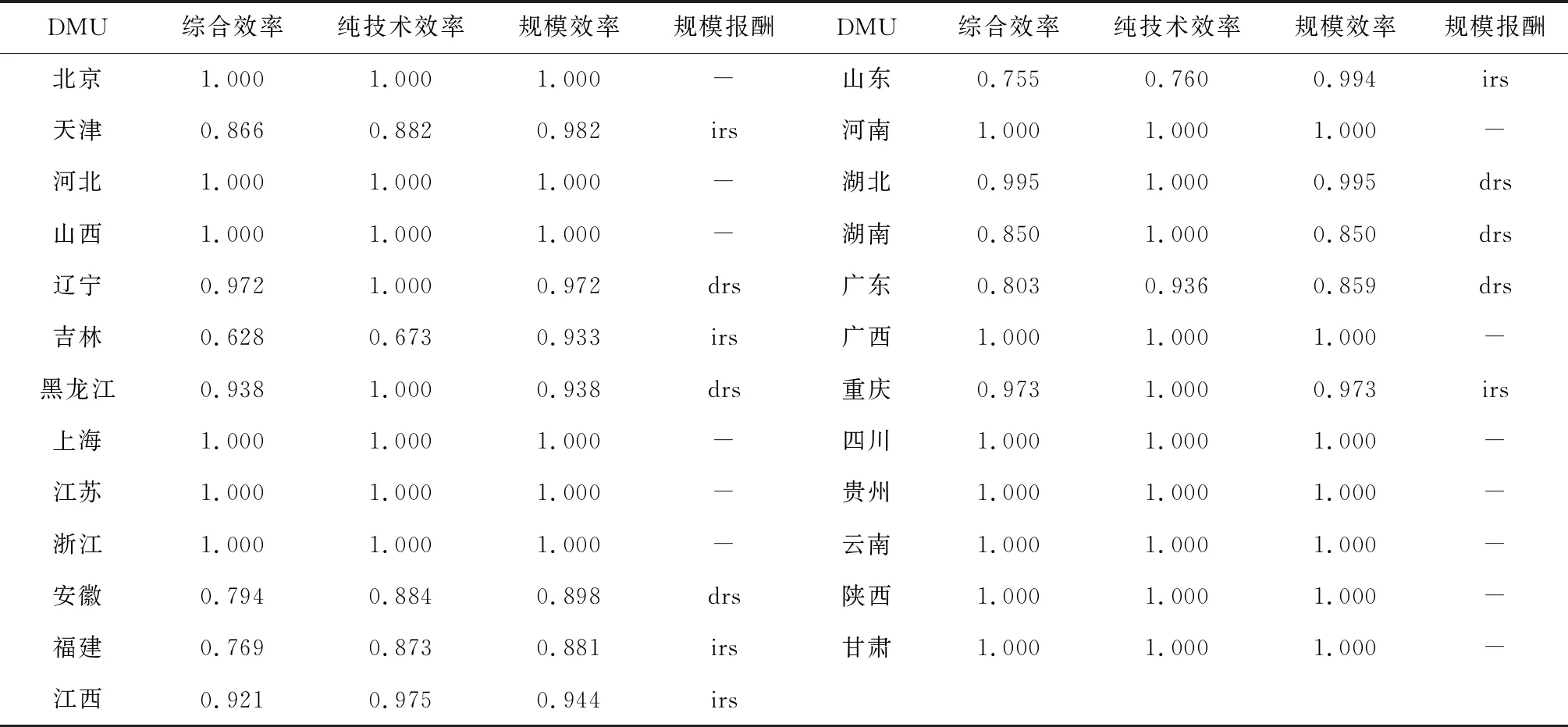
表2 传统DEA模型计算结果
2.2 基于超效率DEA分析
2.2.1创新效率分析 传统数据包络分析对于DEA有效的各省高校效率值都为1,评价单元间的关系难以区别,因此采用超效率DEA模型可解决这一问题。利用MyDEA软件,计算各省份创新效率值及排序,结果如表3所示。从中可得出以下结论:第一,25个决策单元中,贵州省的创新效率均值排名最高,共14个省份都达到了DEA有效,占56%;第二,福建省的创新效率均值排名最低,随后为广东、山东、湖南、吉林、江西、辽宁、天津、湖北、重庆、广西,说明这10个省份的科研创新资源的利用远远不够,还有一定的提升空间,在现有的基础上可产出更多的创新成果;第三,从不同的年份看,山西省在2013年的科研创新效率最高,河南省在2014年及2015年的创新效率表现是最好的,贵州省在2016年及2017年创新效率最高;吉林省2013年的创新效率最低,福建省2014—2017年连续四年创新效率表现最差。
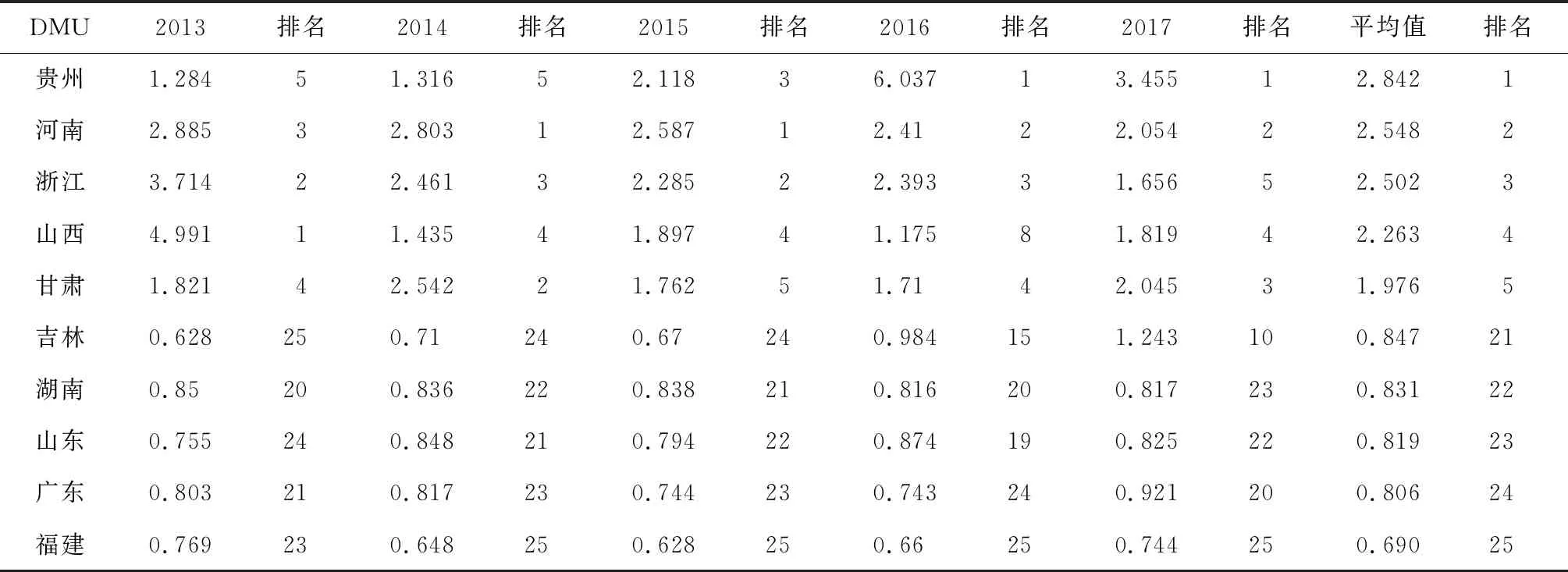
表3 2013—2017年中国省际高校科研创新投入产出效率值及排名
2.2.2创新效率动态分析 中国省际高校综合效率不断变化,为了解高校创新效率的动态变化趋势,绘制综合效率平均值排名前5和后5的省际高校2013—2017年综合效率柱状图,结果如图1、图2所示。从图1可看出,排名第一的贵州省近五年综合效率值整体呈现上升趋势,说明贵州省在技术和管理上创新效率保持稳定发展;河南省从2013年到2017年的综合效率虽然都实现了有效,但是呈现不断下降的趋势;浙江省的创新效率也有所下降,整体呈现波动的状态且综合效率保持有效;山西省的综合效率自2014年下降之后处于在1.5左右波动的状态,总体较平稳;甘肃省综合效率值2013—2017年一直保持稳定的状态,总体呈现稳定的态势。从图2中可以看出,吉林省虽然排名靠后,但从2013年到2017年总体呈现上升的态势,意味着吉林省高校创新效率及创新能力有了很大的提高,一直处于进步状态;湖南省、山东省、广东省、福建省四个省份高校创新效率值一直处于稳定但无效的状态。
2.3 基于GIS空间特征分析
2.3.1空间分布特征 文章采用ArcGis10.2空间分析软件,以超效率DEA模型计算的中国省际高校2013—2017年创新综合效率为数据基础,绘制中国省际高校创新效率分布图(图1)和空间趋势分析图(图2)。由图1可以看出:2013年创新效率集聚区分布在山西、河南和浙江,甘肃、陕西、江苏、云南、贵州、广西的创新效率在1.037~1.820 1之间,新疆、西藏、内蒙古、青海创新效率最低,其余省份为创新效率一般区域。到了2017年,创新效率最高的区域是贵州,其次是甘肃、山西、河南、浙江。从五年的变化来看:中国省际高校的创新效率可分为四部分,第一部分主要分布在贵州、河南、浙江、山西、甘肃地区,创新效率最高;第二部分主要集中在江苏、上海、河北、陕西等地区;第三部分分布在吉林、湖南、山东、广东、福建地区;第四部分主要以西北部地区为主,创新效率最低。空间趋势分析如图2所示,其中,Z轴代表省际高校创新效率值,X轴为东西走向,Y轴为南北走向。从图2可以看出:2013—2017年中国省际高校创新效率曲线呈现出相似的趋势,在东西方向呈现“凸”形,投影线坐落在1格和3格间;南北方向上也呈现“凸”形,投影线坐落在1格和3格间,这表明2013—2017年中国省际高校创新效率东部高于西部,中部高于南部和北部,呈现显著的空间非均衡性。

a. 2013年

b. 2017年
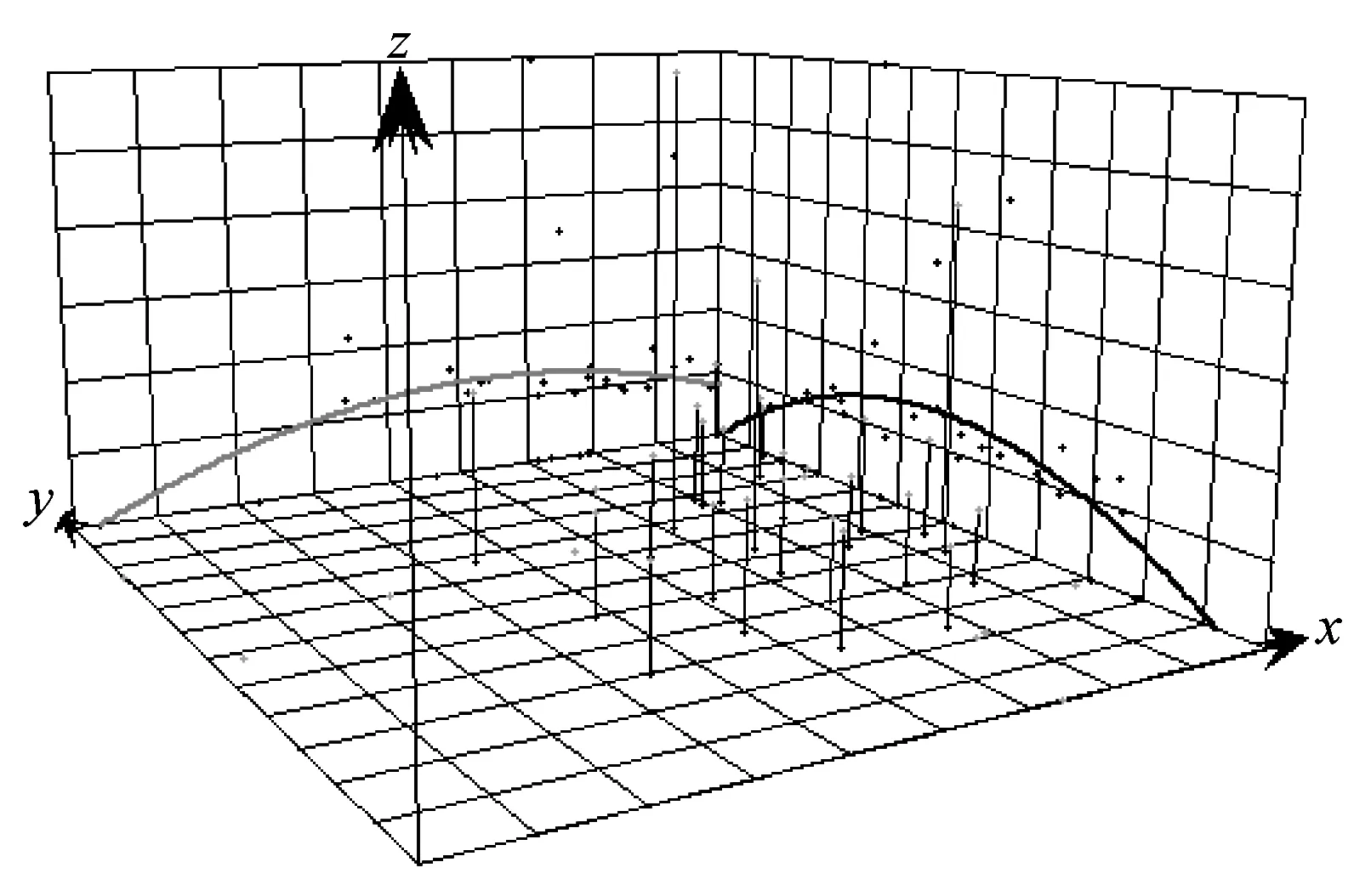
a. 2013年

b. 2017年
2.3.2空间自相关分析 为研究五年内各省高校创新效率的空间集聚特征,绘制Moran散点图并将其结果具体化如表4所示,2013年25个决策单元中,有11个位于第一象限(HH),这说明这几个省份的创新效率较高,并且邻近省份创新效率也较高;有3个位于第三象限(LL),表示这几个省份的创新效率较低,并且邻近省份创新效率也较低;有8个位于第二象限(LH),这几个省份创新效率较低但是邻近地区创新效率较高;有3个省份位于第四象限(HL),广西和甘肃位于第四象限,这两个省份的创新效率远远高于周围地区。2017年25个省份中,有15个位于第一象限(HH);有2个位于第三象限(LL);有6个位于第二象限(LH);有1个省份位于第四象限(HL)——甘肃,是由于甘肃高校的创新效率高于周围地区。结果表明,2013—2017年间各省的科技创新、经济都发生了巨大的变化,尤其是创新效率及其空间分布发生了明显变化,位于第一象限(HH)的省份由11个变为15个。随着时间的推移,中部地区创新效率有很大的提升,同时经济也向中部地区快速发展。
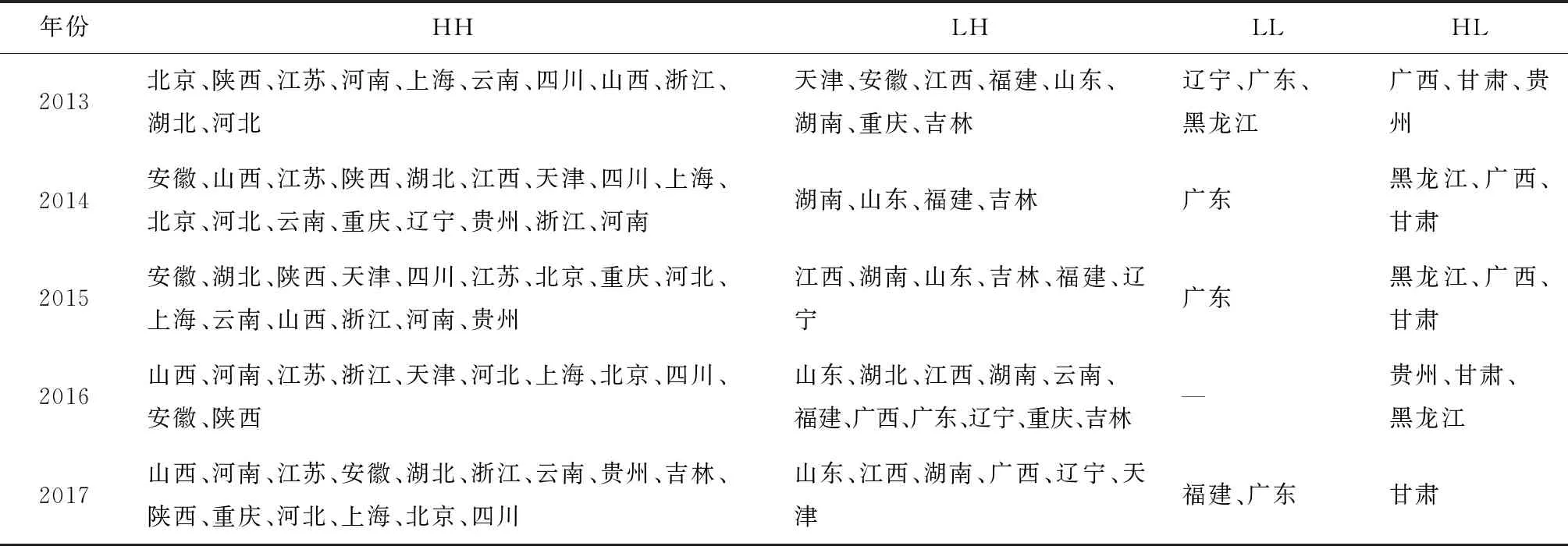
表4 Moran散点图集聚结果
2.3.3空间异质性分析 本研究采用半变异函数分析中国省际高校创新效率空间分布的异质性,对样本数据分别采用球面、高斯、指数等模型进行拟合,选择拟合效果最好的高斯模型进行分析,具体结果见表5。从表5可以看出,2014年空间变异尺度最大,自相关距离为1 266.640 km,在此范围内,各省高校创新效率最为接近,空间依赖性比较明显;2016年和2017年自相关距离最小,最远距离只有1 162.182 km。而偏基台值和块金比则表明,2013年中国省际高校创新效率的块金比为82.72%,说明空间异质性主要由结构性因素引起,其影响程度大于随机因素;2015年中国省际高校创新效率的块金比最小,仅为59.92%,表明也要重视随机性因素对空间异质性的影响。

表5 省际创新效率拟合模型参数
3 结论与建议
通过对中国省际高等院校创新效率和空间分布特征进行分析,本研究得出以下结论:(1)从传统DEA分析结果来看,52%的高校综合效率实现传统DEA有效,其余省份综合效率非有效,除了吉林省创新效率较低以外,各省份创新效率整体较高。(2)从超效率DEA计算出的综合效率来看,56%的高校综合效率实现超效率DEA有效。(3)从空间分布特征来看:第一,2013—2017年中国省际高校创新效率呈现显著的空间特征,东部地区高于西部,中部高于南部和北部;第二,随着时间推移,中部地区的创新效率处于快速发展阶段。空间异质性主要由结构性因素引起但随机因素也不容忽视。
综上所述,实现创新能力的提高,做到以下几点很有必要:首先对于投入资源存在冗余的地区,如天津、安徽、福建等,应合理配置资源利用,提高创新效率,实现最合适的规模报酬;其次吉林省此类虽然创新效率排名靠后的省份,国家可以给予更多的财政支持,鼓励建立内部创新效率机制,清楚地了解自身的创新效率,以提高创新效率;最后对于西北地区创新效率较低的地区,政府部门给予更多的科技经费,同时根据自身的地域特点,选择比较有自己专项特色的领域进行创新,合理配置资源向周边地区学习。

