劈裂岩体结构面直接剪切试验研究

邢文政，王硕，范鹏贤，陈昊祥，王德荣

(1.陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏南京，210007；2.北京建筑大学土木交通学院，北京，100044)

深部岩体具有显著的结构性，其破坏过程取决于长期压缩储存在其结构内部的能量沿结构面的传递、耗散和转化[1−2]。在不同初始条件和外在扰动的影响下，宏观的破坏形式可表现为能量的突然释放(饼化破裂、即时型岩爆、崩塌)、滞后释放(滞后型岩爆、慢波、蠕变加速等)或缓慢的耗散(时效变形、分区破裂、蠕滑等)。这些大小不同的结构面极大地影响了工程围岩结构的稳定性[3]。

水利水电、深部采矿、交通隧道等领域的工程经验表明，结构面的分布及其性质往往是决定工程安全的关键因素之一。如发生在锦屏二级电站引水隧洞的特大岩爆事故即与隧洞附近的结构面密切有关[4−5]。在采矿领域，SNELLING等[6]分析了加拿大Creighton 矿中围岩地质构造、应力状态和矿震之间的关系，指出地质构造对矿区围岩应力场起控制作用。ZHAO 等[7]分析了木城涧煤矿的15 起岩爆事件，发现断层、褶皱、岩/煤层变化等对岩爆发生有重要影响，尤其是从厚煤层向薄煤层推进时，岩爆更易发生。在国防工程领域，WANG 等[8−9]研究了爆炸冲击作用下节理岩体的动力响应问题，并提出了诱发岩体失稳的计算理论。

天然岩体中存在大量的结构面，这些结构面显著地影响着工程岩体的强度和稳定性[10]。特别是在深埋地下工程中，岩体具有较高的初始应力，由于开挖卸荷扰动，以及由此引起的应力重分布和应力集中，极易诱发高度积累的应变能沿着断层、节理等薄弱边界释放，从而危及工程围岩的安全与稳定。预测岩石天然结构面的抗剪强度对于岩石工程的稳定性分析和支护设计至关重要。

对于岩体结构面的研究由来已久。PATTON[11]考虑了爬坡和切齿效应，通过单一规则齿状结构面的直剪试验，提出了PATTON 双直线模型。BARTON 等[12]则基于节理粗糙度参数提出了结构面剪切强度模型，该方法被国际岩石力学学会推荐为评估结构面粗糙度的标准方法[13]。SCHNEIDER[14]通过对复制节理的研究，提出了考虑结构面剪胀角衰减规律的经验公式。GRASSELLI 等[15]考虑了沿剪切方向的爬坡区域对结构面剪切力学行为的影响，根据剪切方向倾角和有效接触面积比拟合得到节理面粗糙度参数，据此提出结构面剪切强度公式。然而，由于结构面强度和稳定性本身的复杂性，该问题至今仍然是岩石力学领域的研究热点。

近几年来，MAGSIPOC 等[16]对2D和3D 结构面形貌表征方法进行了系统的总结。LI等[17]系统总结了PATTON 以来的主要剪切强度模型并提出了剪涨角表达式。周辉等[18−25]通过试验手段研究了在不同工况下的岩体结构面剪切变形破坏过程及其影响因素，结果表明，岩体不连续面的剪切稳定性主要受3个因素即不连续面的形态、法向应力水平以及材料的强度特性控制，但这三者之间以及这三者与结构面赋存环境的相互关系目前仍未形成共识。对于复杂结构面，基于大量实验数据的实证研究仍然是必不可少的。

本文作者通过石膏拓模方法批量复制岩石劈裂结构面，通过恒定正应力的直剪试验，研究结构面形貌特征、法向应力和结构面壁材料强度对结构面剪切抗力的影响规律，并基于试验数据对经典的BARTON 模型进行修正，改善其在高法向应力条件下预测值偏低的问题，使之能够适应较高的地应力环境。

1 试件制备与试验方法

1.1 结构面试件制备

具有相同形貌特征和力学参数的结构面难以批量复制一直是制约结构面试验的因素之一。采用规则形貌结构面可以避免这一难题，但与实际岩体结构面的差别无法量化。而通常的拓模方法往往会损坏结构面的细观特征，无法多次复制。本文选用强度较高的花岗岩长方体经劈裂制备原始的粗糙结构面，拓模前采用EinScan-Pro 多功能手持式3D 扫描仪扫描结构面形貌(扫描精度为0.2 mm)，而后经反复比选试验，优选α型早强石膏粉作为拓模介质，解决了岩石结构面的高效批量复制的难题。

相较于目前常用的倒模法，本文采用的制模方法可以同时制作上下盘试样，且制备好的试件因略微干缩可自动脱落，不会对原岩结构面造成损伤，同时其细节复制的保真率一般比3D打印的高。具体的制模流程为：首先向浇筑盒内的结构面均匀喷涂油性脱模剂，缓慢倒入石膏浆，轻轻敲击盒侧壁使气泡溢出，阴凉通风处静置1 h后拆模便可得含结构面形貌特征的石膏模板。然后使用石膏模板按照相似步骤制备含结构面形貌特征的水泥砂浆试件。水泥砂浆试件养护24 h后拆模，石膏模板可继续用于浇筑新试样。

选用水泥砂浆为模拟材料，通过α型石膏粉拓模法，制备了48块结构面试件。所有的试件根据形貌特征和材料强度分为12组(4种形貌参数和3种材料强度)。试件材料强度配比有3种，水、水泥和砂的质量比分别为1:2.3:5.5，1:2.3:5.0和1:2.3:4.5。经立方体单轴抗压强度测试，3种配比水泥砂浆的单轴抗压强度分别为32.14，40.82和53.01 MPa。利用倾斜试验测定试件的基本摩擦角为32°。

试件制备后，抽取一定数量的结构面试件，采用3D 扫描仪对其形貌特征进行扫描，通过CloudCompare 软件对比原岩结构面点云数据和水泥砂浆试件点云数据来检验试件制备的精度，若2个相同位点的高度数据差值小于扫描精度0.2 mm，则认为该相同位点的2个结构面形貌特征相同，反之则不同。制备试件结构面的保真率分析过程见图1。随机抽取的5 个试件的保真率分析结果见表1。由表1可知：复制试件的保真率平均值为98.418%，具有很好的复制效果，且标准差小，具有很好的稳定性。

表1 随机选取试样的保真率Table 1 Fidelity of randomly selected samples

图1 试件结构面保真率分析示意图Fig.1 Schematic diagram of fidelity analysis of rock joints replicas

1.2 结构面特征表征

结构面粗糙度的表征对结构面剪切强度的预估具有重要意义。节理粗糙度系数是一个广泛使用的二维表面粗糙度表征参数[13]，用CJR表示。在本文中，CJR由结构面上10个均匀分布的测线(参考图2)的平均值确定。采用TES等[26]提出的坡度均方根法计算4组节理的粗糙度，CJR计算结果见表2。

表2 4组结构面的CJRTable 2 CJR of four groups of joints

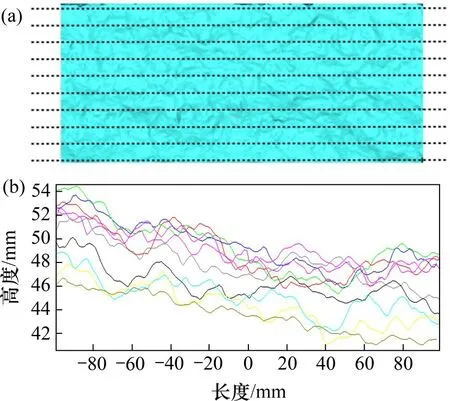
图2 确定结构面形貌参数CJR的方法Fig.2 Determination of joint roughness coefficient(CJR)

1.3 试验方法

直剪试验在ZW-30B型微机控制岩石直剪仪上进行，该试验机由加载装置、微机控制系统、应力−应变测量装置等组成。该设备可通过力和位移2种模式进行控制，切向加载能力为1 000 kN，法向加载能力为300 kN。

结构面直剪试验在常法向应力条件下进行，加载路径如图3所示。图3中：σ0为结构面所受法向应力；τp为峰值破坏型曲线的峰值剪切强度；τc为峰值破坏型曲线的剪切残余强度；τ0为滑动破坏型曲线的峰值剪切强度；u1和u2为破坏曲线达到峰值剪切强度所对应的剪切位移；t1为施加法向应力达到相应值所对应的时间；t2，t3和t4分别为试验达到剪应力τp，τc和τ0时所对应的时间。试验中，法向荷载通过力控制，切向荷载通过位移控制，法向加载速度为0.2 kN/s，切向加载速度为0.02 mm/s。为了观察不同法向应力下结构面破坏特征和剪切强度变化规律，试验设置了4个法向应力，分别为1.0，3.0，5.0和10.0 MPa。

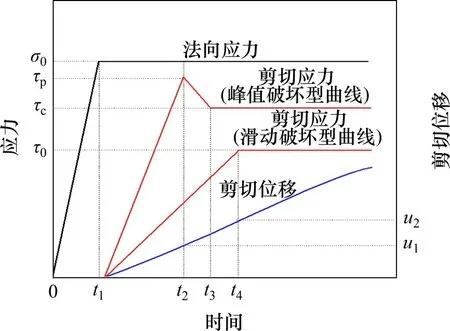
图3 剪切加载路径示意图Fig.3 Schematic diagram of loading path of shear tests

2 主要试验结果及其分析

根据上述应力路径，对4组结构面开展了不同法向应力水平和不同材料强度的直剪试验。借助伺服控制软件记录轴向力、轴向位移、切向力和切向位移等试验数据。

2.1 剪应力−位移曲线

对试验结果进行整理，绘制剪切应力位移曲线图。限于篇幅，仅给出材料强度为53.01 MPa的试件组的结果，如图4所示。从图4可以发现：

图4 剪切应力−位移曲线Fig.4 Curves of shear stress−displacement

1)在应力达到峰值剪切强度前，应力位移曲线大致呈线性关系。一般情况下，随法向应力由1.0 MPa 提高到10.0 MPa，峰值前的应力位移曲线斜率越来越大。

2)到达峰值剪切强度后，应力随不同法向应力条件呈现不同的变化趋势。在低法向应力(1.0 MPa和3.0 MPa)下，峰值后剪切应力基本不降低；在中等法向应力(5.0 MPa)下，峰值后应力多随剪切位移的发展有所降低，但降低幅度不大；当法向应力为10.0 MPa 时，多数试件在剪切力峰值后剪切抗力会随位移出现明显降低。

3)结合另外2 组材料强度的试件的结果可知，相同材料强度的试件，残余剪切强度基本一致；残余强度受法向应力影响大，形貌参数对残余强度影响较小。

4)在高法向应力下，结构面的应力位移曲线关系多表现为峰值剪断型曲线，即剪切应力到达峰值后会出现明显下降，随后缓慢趋向于残余强度并最终基本保持不变；在中低法向应力下，结构面应力位移曲线形态多表现为滑动破坏型曲线，剪切应力达到最大值后并不会随变形的发展明显降低。

图5所示为不同法向应力下结构面试件的磨损情况。由图5可知：在低法向应力条件下，结构面主要以爬坡效应为主，剪断的微凸体数量较少，形貌面改变不大；达到峰值剪切强度后，抗剪强度主要依靠摩擦提供。因此，应力位移曲线关系呈现滑移型曲线；在高法向应力条件下，被剪断的微凸体数量较多，形貌参数发生较大改变；达到峰值强度后，结构面复杂程度的降低导致剪切强度的降低；当形貌面参数不再发生较大改变时，剪切强度也不再降低。

图5 不同法向应力下结构面试件的磨损情况Fig.5 Wearing of joints specimens at different normal stresses

岩石结构面的剪切强度主要由基本摩擦强度、剪胀强度和微凸体剪断的强度构成。基本摩擦强度通常通过基本摩擦角的形式表现，由于基本摩擦角通常假定为常数，所以，岩石结构面在不同法向应力下的剪切行为取决于法向的膨胀和微凸体的剪切。在低法向应力下，因为结构面两侧的微凸体相互压紧程度低，容易发生滑动，微凸体的剪断可忽略，因此，法向的膨胀主导剪切行为。当施加足够大的法向应力时，法向膨胀受到限制，位移发展过程中微凸体相继被剪断，由此导致结构面粗糙程度降低，最终达到新的稳定平衡，结构面抗力不再降低。

2.2 峰值剪切强度

通过对数据的处理，所有试件的峰值剪切强度如表3所示。

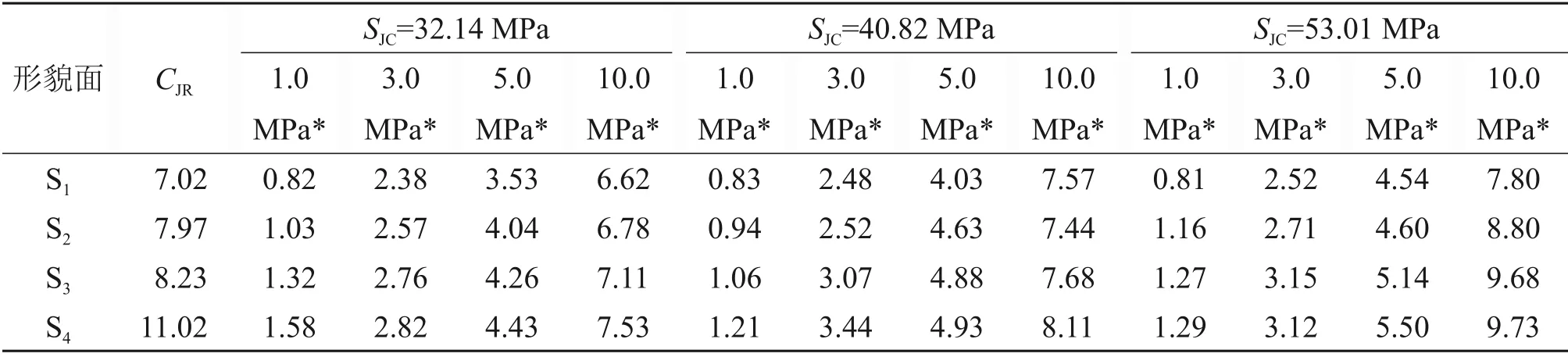
表3 结构面峰值抗剪强度试验结果Table 3 Test results of peak shear strength of joints MPa

结构面峰值剪切强度在材料强度方面的规律不明显。当法向应力较高(5.0 MPa和10.0 MPa)，SJC=53.01 MPa 时(SJC为结构面壁材料强度)的峰值剪切强度最大，SJC=32.14 MPa时的峰值剪切强度最小，SJC=40.82 MPa 时的峰值剪切强度介于两者之间，这反映出高材料强度的结构面在剪切时，剪断同样的微凸体需要更大的剪切力，微凸体能够为结构面提供更强的抗剪强度。而当法向应力较低时，试件在剪切时以爬坡为主，微凸体剪断较少，材料强度的影响不明显。

一般而言，形貌面特征越复杂，结构面提供的抗剪强度越高，将粗糙度指标与结构面强度的关系进行线性拟合，结果如图6所示。在拟合时，假设CJR=0，结构面的抗剪特性与倾斜试验一致，即固定其在Y轴上的截距。从图6可以看出：CJR越大，其对应的剪切强度越高；在不同法向应力条件下，峰值剪切强度与节理粗糙度系数均呈现较强的正相关线性关系。

图6 CJR与峰值剪切强度的关系Fig.6 Relationships between CJR and peak shear strength

BARTON等[12,27]通过总结试验数据提出了结构面峰值剪切强度公式：

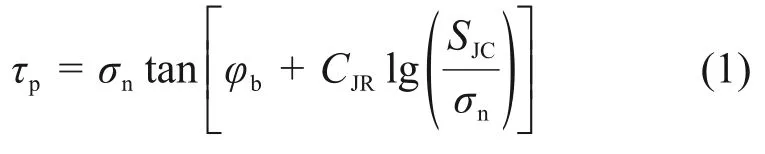
式中：τp为峰值剪切强度；σn为作用在接触面上的法向应力；φb为节理面基本摩擦角。

从图6可以看出，在低法向力条件下，BARTON 模型基本能预测结构面的剪切强度，但在高法向力条件下，该模型的预测精度受材料强度的影响，当材料强度较低时，BARTON 模型预测值略比实际剪切抗力高，在材料强度较高时，则明显比实际试验值低。

2.3 结构面形貌参数的影响

表4所示为以最简单的结构面(S1)的峰值强度为基准，对所有测试结果进行归一化处理的结果。

由表4可知：在高法向应力状态下，形貌面特征之间的差异对结构面峰值抗剪强度影响小，而在低法向应力条件下，形貌面特征对结构面峰值抗剪强度影响大。在3 种材料强度下(由低至高)，当正应力为10.0 MPa时，最复杂的结构面(S4)比最简单的结构面(S1)的峰值强度分别高14%，7%和25%；当正应力为1.0 MPa 时，最复杂的结构面(S4)比最简单的结构面(S1)的3 个峰值强度分别高93%，46%和59%。当CJR相同时，相比于最简单的结构面(S1)，峰值强度提高的比例与法向应力呈现负相关关系，即法向应力越高，结构面峰值强度提高的相对量越少，这一规律应与结构面的破坏机理有关：在低法向应力条件下，结构面主要以爬坡效应为主，形貌面特征对峰值强度影响大；在高法向应力条件下，结构面主要以切齿效应为主，形貌面微凸体基本被剪断，形貌特征的影响被削弱。

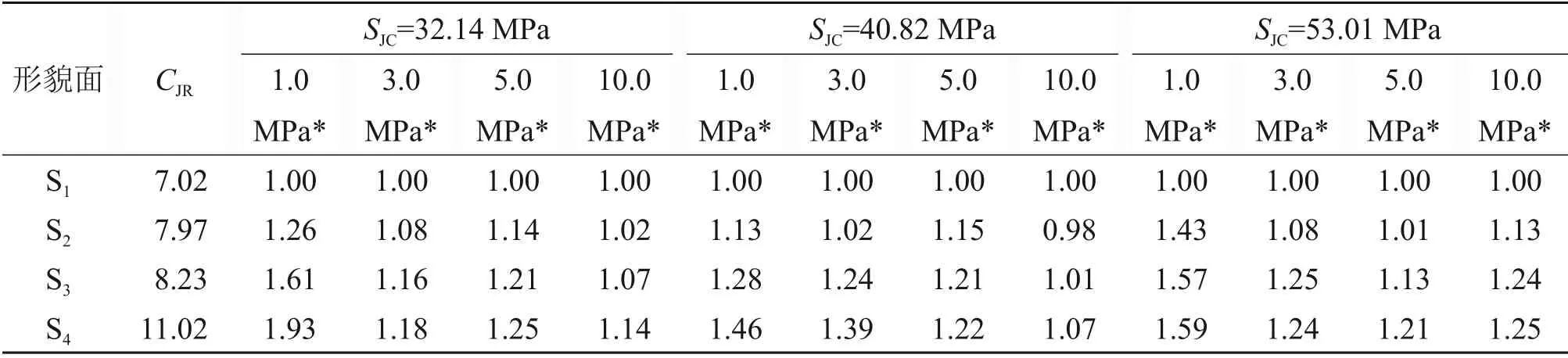
表4 归一化剪切强度结果Table 4 Normalized shear strengths

3 剪切强度估计模型

3.1 与BARTON模型预测值的对比分析

对式(1)进行简单变形，可得

对照组：共41例，男22例，女19例；年龄范围50～76岁，年龄（63.9±7.6）岁；原发心脏病为高血压性心脏病15例、冠状动脉性心脏病20例、扩张型心肌病4例、瓣膜性心脏病2例；美国纽约心脏病学会心功能分级Ⅲ级27例、Ⅳ级14例。

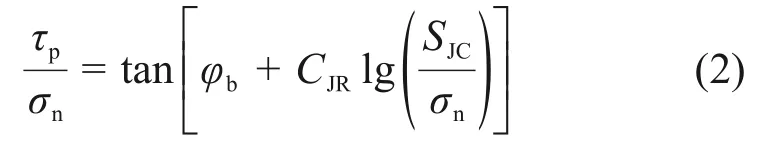
对表3中的试验数据进行简单处理，可得峰值剪切强度和正应力的比值(即应力比)，如表5所示。

表5 结构面峰值抗剪强度与正应力的比值Table 5 Shear strength/normal stress ratio of joints

将表5中的数据绘制成图并与BARTON 模型预测值进行对比，其结果如图7所示。

从图7可以看出：总体上BARTON 模型预测值与实测值的变化规律基本一致，尤其是在材料强度较低而正应力相对较高时(图6(a)中右侧)，BARTON 模型很好地反映了应力比随正应力的变化趋势，但试验结果与BARTON 模型预测结果在很多地方仍存在较大差异。

图7 应力比试验结果及与BARTON模型对比Fig.7 Stress ratio of tested samples and comparisons with BARTON'model

总体上，BARTON 模型中CJR的影响相对较小，因而不同CJR结构面的应力比曲线靠得比较紧密，也就是说，由于结构面形貌导致的应力比预测值的波动范围均比实测值偏小。这种稳妥的设计使得BARTON 模型预测结果不会与实测值偏差过大，但同时也限制了其在特定条件下的预测精度。当SJC=32.14 MPa，法向应力为1.0 MPa时，实测的应力比范围为0.82～1.58，而BARTON 模型预测应力比范围为0.92～1.14。当正应力增大或材料强度增大时，两者差别有所减小，但仍然明显低估了CJR的影响。

当正应力为10.0 MPa，结构面壁强度较低(SJC=32.14 MPa)时，BARTON模型预测应力均比实测值大，应力比平均偏大5.2%；而当结构面壁强度较高(SJC=53.01 MPa)时，BARTON模型预测应力比均比实测值低，应力比平均偏低12.5%；当SJC=40.82 MPa 时两者相差不大。这反映了在较高正应力作用下，不同材料强度的结构面剪切时的变形破坏机制有所差别，而BARTON 模型对此考虑不足。根据BARTON模型，CJR的影响将在正应力等于SJC时消失，而后其影响为负值，这显然是不合理的。

3.2 对BARTON剪切强度模型的改进

由于BARTON 模型参数少，且能基本反映主要影响因素对结构面剪切强度的影响规律，因此，大部分剪切强度模型基于该模型进行改进。改进的方向主要有2 个：一是在BARTON 模型的第二项中加入乘子[28]，二是修改BARTON 模型公式中剪胀角的表达式或增加修正项[25,29−31]。很多改进模型放弃了广为应用的CJR参数，为模型的推广应用带来了不便。

为反映剪切破坏过程中剪胀爬坡和微凸体剪断不同的力学机制和变化规律，本文提出以下修正公式：

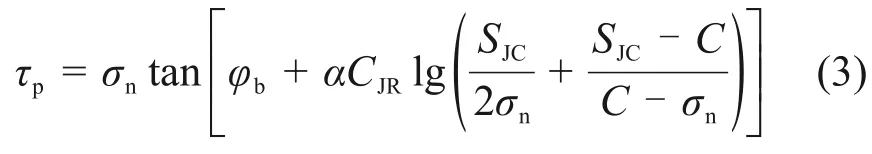
式中：α为拟合参数；C为材料强度修正基准值。

为了准确量化CJR的影响，常数C用于校正结构面材料强度变化的影响，其取值一般介于最大正应力水平和材料强度之间。对数项中的第一项代表剪胀对剪切抗力的贡献，随正应力增加而减小；第二项在一定程度上反映了微凸体剪断对剪切抗力的贡献，随材料强度和正应力增大而增大；2个子项在正应力增大过程中此消彼长，与结构面变形破坏机制更加吻合。分析表明，在低正应力条件下，剪切强度预测值对于C的变化不敏感；在高正应力条件下，C变小时预测值略有增大。

图8所示为改进模型与试验数据的对比，其中α取1.7，C取30.0 MPa。从图8可以看出：本文改进模型在大多数情况下更接近试验数据，不仅可以更充分地反映CJR的对剪切强度的影响，而且有效解决了BARTON 模型在高正应力条件下的预测值偏低的问题，但在材料强度较高且正应力较高时，本文模型预测值仍然略偏低。

图8 改进模型估计与试验数据的对比Fig.8 Comparisons of tested data and estimation of proposed model

直接比较抗剪强度易掩盖低正应力条件下的剪切强度估计误差，而应力比更易凸显抗剪强度变化趋势。为此，绘制了应力比随正应力变化的曲线(图9)。从图9可以看出：相对于图7中的BARTON 模型，本文模型应力比的曲线分布更合理，其原因是：1)不同CJR时，应力比曲线分布范围更宽，更接近试验值；2)在中高正应力区，整体性的偏差得到了校正，如在10.0 MPa 正应力条件下，当SJC=53.01 MPa 时，BARTON 模型预测值的平均误差为12.07%，本文模型预测值则较试验值平均低4.8%。由于每种工况的结构面只进行了1次试验，试验数据具有一定的离散性，仍然存在少部分数据点与改进模型的数据点偏离较远。

图9 改进模型的应力比与试验数据的对比Fig.9 Comparisons between stress ratio of tested data and proposed model

3.3 结构面剪切的方向性

众所周知，结构面剪切具有方向性，沿爬坡方向和沿下坡方向的剪切抗力有显著不同。而CJR指标本身无法反映剪切的方向性，因此，存在这样的可能：具有同样CJR参数的结构面，由于开展直剪试验时剪切的方向不同，导致测得的剪切强度存在较大的偏差，从而使相应的数据点与既定规律(如CJR=7.02 时应力比并未随正应力的增加而单调下降)一致性被削弱。为了验证该想法，开展了6 组标记剪切方向的直接剪切试验，图10所示为相应的试验结果。

从图10可以看出：对于材料强度较高的结构面，在3.0 MPa和10.0 MPa的正应力条件下，不同方向的剪切强度分别相差8%～25%和8%～12%，可以明显地分为正剪和反剪2 组，且当正应力较大时，正反剪切的强度相对偏差更大；在3.0 MPa正应力条件下，BARTON 模型的预测值落于2 组之间，而在10.0 MPa 正应力条件下则偏低；与此同时，在3.0 MPa正应力条件下，本文模型预测值与爬坡方向的测试结果接近，在10.0 MPa 正应力条件下则落于2 组之间。由于CJR无法描述结构面沿剪切方向的相对高低，若想进一步提高模型的预测精度，需要引入考虑剪切方向的形貌参数[16]。

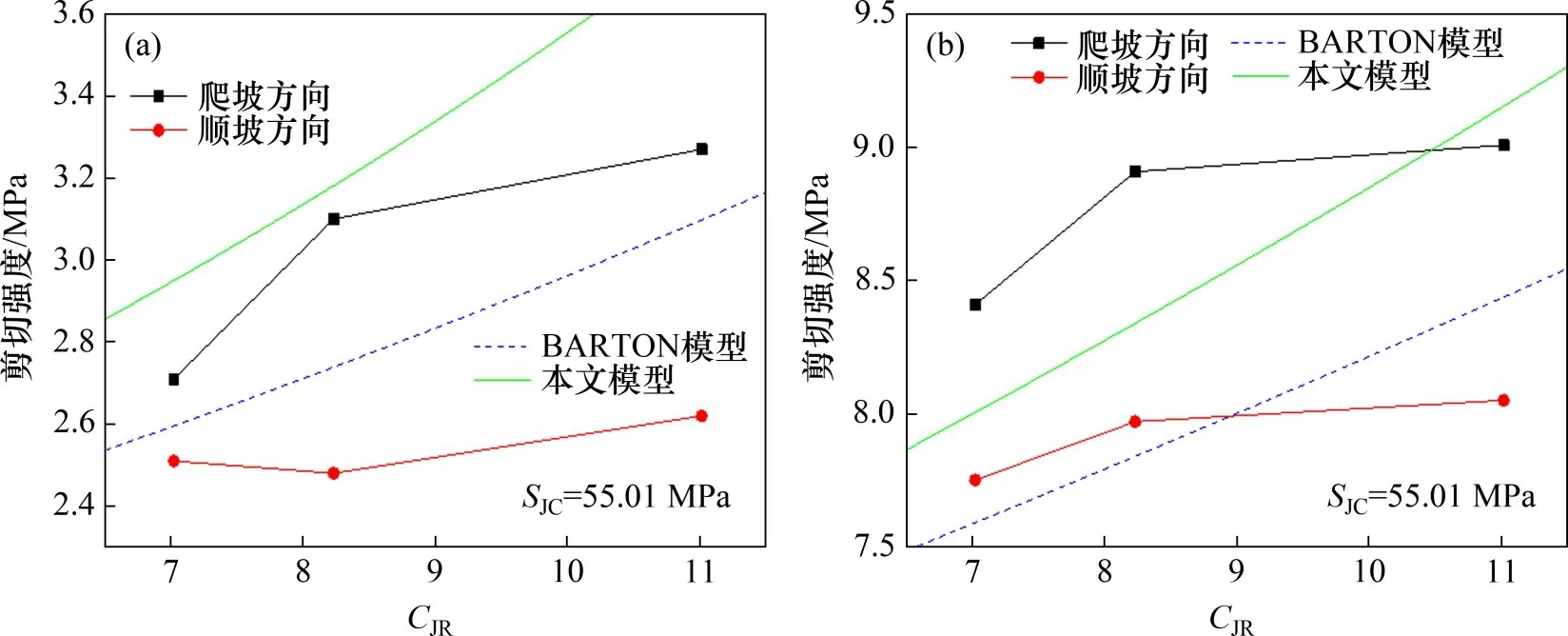
图10 改进模型的应力比与试验数据的对比Fig.10 Comparisons between stress ratio of tested data and proposed model

4 结论

1)结构面的变形破坏过程主要表现为2 种形式：在低法向应力条件下，应力位移曲线关系表现为剪切滑移型，残余强度和峰值剪切强度相差不大；当法向应力较高时，应力位移曲线关系多表现为峰值剪断型。

2)结构面峰值剪切强度随结构面粗糙度参数、结构面壁材料强度和正应力水平的增加而提高，结构面粗糙度参数的对剪切强度影响在高正应力条件下趋于减小。

3)本文模型能够更好地反映CJR对剪切强度的影响，提高了在高正应力条件下的预测精度。