基于蠕变损伤演化模型的深部高地应力隧道双层初期支护力学特性研究
马杲宇,何川,陈子全,马春驰,杨文波,赖孝辉
(1.西南交通大学交通隧道教育部重点实验室,四川成都,610031;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都,610059)
穿越高地应力软岩地层的隧道在施工过程中可能会遭遇严重的挤压性大变形。传统的隧道支护形式难以满足对围岩变形控制的需求,因此,会出现围岩变形侵限、钢拱架扭曲、二次衬砌混凝土开裂等病害[1]。此外,位于高地应力场中的软弱岩体具有显著的流变特性[2],国内大量软岩隧道的工程实践表明,隧道支护结构自身位移和承受的围岩荷载在施工期及建成初期就呈现出随时间延长持续增加的趋势[3−5]。陈宗基等[6]认为隧道周边岩体的膨胀和流变效应是导致隧道在施工过程中发生挤压性大变形的重要因素。如果不采取合理的支护措施,隧道衬砌在施工和运营过程中将面临严峻的失稳破坏风险。
目前,人们对高地应力软岩隧道的支护措施和施工期围岩的时空效应进行了大量的研究:BARLA 等[7]利用黏弹塑性本构模型,通过有限差分法计算了一种让压支护体系在里昂—都灵隧道斜井软岩段施工期间的力学特性,分析了数值结果和现场监测数据。汪波等[8]分析了目前软岩大变形隧道主要采用的及时强支护、分层支护和让压支护的承载机理,并提出了这3种支护型式的优缺点和适用范围。张德华等[9]依托西成专线阜川隧道,通过现场监测和数值计算研究了炭质页岩段双层初期支护的支护效果,优化了支护结构的参数和第二层初期支护合理的施作时机。孙钧等[10]利用线−弹性模型和弹−黏塑性模型分别模拟隧道开挖时围岩的空间效应和时间效应,并结合现场监测数据比较了采用不同施工工法时隧道的变形规律和力学特性。
软弱岩体内部层理面、结构面等损伤发育具有一定的各向异性,不再满足均一性假设。随开挖卸荷作用及围岩蠕变变形的不断加剧,岩体内部损伤将持续发展,传统的黏弹塑性本构模型已难以反映工程实际。针对这一问题,人们引入蠕变损伤演化模型,并通过室内试验等手段研究裂损岩体的力学特性。朱维申等[11]考虑节理对岩体力学特性的影响,利用基于西原模型的蠕变损伤本构,计算了地下洞室群开挖后变形的长期发展情况。HAQUE 等[12]基于2 种不同的蠕变损伤模型,计算了不同应力加载水平下试件变形的时效特性,并通过试验结果对计算进行了验证。KABWE等[13]利用能描述各向同性损伤的分数阶弹簧−黏壶元件构建蠕变本构模型,并利用该模型分析了位于挤压性大变形地层中的隧道变形量及围岩损伤的分布范围。黄耀英等[14]分别建立了岩体和节理的流变损伤演化函数,并编写了相应的有限元计算程序,对某节理岩质边坡开挖后的位移进行了分析。CAO 等[15]根据断裂力学理论,考虑岩体内部裂隙和空洞的发展,推导了能反映从瞬时弹性变形到加速蠕变变形全过程的蠕变本构,并计算了岩体在不同荷载等级下的时效变形特性。
然而,现有的研究成果仍存在一定的不足:针对软岩隧道的新型支护措施和施工期力学特性的研究,主要采用传统的弹塑性计算和现场监测的手段,很少考虑岩体的时效特性对隧道施工的影响,这会导致计算得出的位移和围岩压力偏小,不利于隧道结构的长期安全设计。对岩体蠕变损伤的分析主要基于样本的室内试验数据,难以反映岩体所处的实际环境,缺乏具体的工程实践应用。因此,本文以成兰铁路茂县隧道为依托工程,利用蠕变损伤模型,通过有限差分软件FLAC3D对比分析单层初期支护和双层初期支护工法在隧道施工期的力学行为,并与现场监测的数据进行对比,探究双层初期支护的承载机理。研究结果可以为高地应力软岩隧道施工和支护方法设计提供一定的参考。
1 工程概况
成兰铁路茂县隧道临近龙门山断裂带,区域构造运动强烈,隧址区最大水平主应力约为37 MPa。隧道的设计长度为9 955 m,最大埋深约为1 650 m。茂县隧道所处区域水文地质环境较为复杂,隧道沿线主要分布志留系茂县群炭质千枚岩、泥质灰岩、绢云母千枚岩和砂岩等。这些岩体的单轴抗压强度较低,自稳能力弱,在高地应力场中具有显著的蠕变特性。此外,受到西南区域多次强烈地震的影响,岩体内部存在大量震裂损伤,结构面和节理发育,茂县隧道的纵断面如图1所示。

图1 茂县隧道纵断面图Fig.1 Profile of Maoxian tunnel
茂县隧道穿越的F1 茂县—汶川断裂为活动断层,宽度约为400 m,断层整体与水平面夹角为73°,其对隧道施工的稳定性有较大影响。掌子面揭露的F1 断层处的围岩为近似竖直的陡倾层状炭质千枚岩,其倾角为87°,岩体结构破碎,层理面极为发育,图2所示为断层斜井掌子面处揭露的千枚岩岩体。室内试验测得此段千枚岩样本的单轴抗压强度为2.41 MPa,围岩的强度应力比为0.11,尽管位于该断层破碎带处的茂县隧道1号斜井埋深相对较浅约480 m,但在施工中仍出现了严重的挤压变形,并出现了混凝土开裂、钢拱架扭曲和锚杆垫板松脱等病害,如图3所示。

图2 隧道掌子面破碎千枚岩Fig.2 Brokenphyllite at tunnel face

图3 隧道挤压大变形示意图Fig.3 Schematic diagrams of large squeezing deformation of tunnel
2 现场实测
为研究双层初期支护的承载机理和施工期隧道支护结构的力学行为,在茂县隧道F1 断层正洞试验段分别选择单层初期支护断面(K127+832)和双层初期支护断面(K127+936)对支护结构的受力开展长期监测,双层初期支护的施工过程如图4所示。

图4 第二层初期支护现场施工示意图Fig.4 Schematic diagram of construction of second primary support
监测项目主要包括利用土压力盒测量围岩压力、双层初期支护之间、初期支护和二次衬砌之间的接触压力以及通过应变计测量二次衬砌混凝土应变,监测元件的布置方式如图5所示。

图5 监测元件布置图Fig.5 Distributions of monitoring instruments
2.1 单层初期支护的力学特性
由于F1 断层处的千枚岩为陡倾产状,支护结构左、右两侧的围岩压力近似呈对称分布,因此,仅选取拱顶以及左侧测点的监测结果。当采用单层初期支护工法时,监测断面处的接触压力曲线如图6所示。

图6 采用单层初期支护时的接触压力Fig.6 Pressures with single primary support method
由图6(a)可知:在陡倾层状岩体的影响下,茂县隧道围岩的挤压作用主要位于层理面法线方向。现场调研结果显示,隧道变形和破坏的位置均集中在拱腰位置,拱腰处的最大围岩压力为1 301 kPa。围岩压力的最小值出现在顶处位置,为638 kPa。隧道施工后围岩压力迅速增大,施作二次衬砌后,围岩压力的增长速度随之降低。拱顶位置的围岩压力最快趋于稳定,而拱腰处围岩压力增长速率的降幅最小,在二次衬砌施作后250 d时拱腰处的围岩压力仍保持增长趋势。
由图6(b)可知:初支与二衬之间的最大接触压力仍位于拱腰位置,为831 kPa,拱脚、拱肩和拱顶处的接触压力分别为721,593和512 kPa。在二次衬砌施作后的75 d 内,荷载的增长较迅速,而后增长率逐渐降低并趋于稳定。由于隧道周边千枚岩体自承能力不足,二次衬砌分担的荷载占围岩总压力的69.1%,比采用传统新奥法施工隧道的荷载分担比例大,二次衬砌成为隧道的主要承载结构。在隧道运营期间,若围岩的蠕变变形持续发展,则二次衬砌作为安全储备的功能将下降。
2.2 双层初期支护的力学特性
第二层初期支护的施工滞后第一层初期支护约25 d,其结构形式与第一层初期支护完全相同,二次衬砌在第二层初期支护施作后的第55天施工。双层初期支护断面的现场监测结果如图7所示。
由图7(a)可知:当采用双层初期支护时,最大围岩压力与单层支护的断面相比明显下降。第一层初期支护拱腰、拱肩、拱顶处的围岩压力分别为1 029,799和564 kPa,与单层初期支护断面相比,拱腰处的围岩压力降低了20.9%,各测点围岩压力平均降低了15.6%;监测断面围岩压力的增长速率在二次衬砌施作后迅速降低,最终在隧道开挖200 d左右趋于稳定。这表明双层初期支护通过分步卸荷作用,降低了围岩内部的应力,进而减小了高地应力环境中千枚岩的流变特性。
由图7(b)和(c)可知:初期支护之间的接触压力从拱腰到拱顶依次为789,624和394 kPa,约占围岩总压力的26.7%。二次衬砌与初期支护在拱脚、拱腰、拱肩、拱顶的接触压力分别为406,471,367和330 kPa。二次衬砌分担的围岩荷载比例约为49.6%,与单层初期支护断面相比降低了28.2%。由此可见,双层初期支护能够承担较大的围岩荷载,二次衬砌承担的荷载比例显著降低,隧道在运营期可以获得更多的安全储备。

图7 采用双层初期支护时的接触压力Fig.7 Pressures under double primary support method
3 数值计算
3.1 蠕变损伤演化本构模型的定义
软弱岩体的蠕变变形主要包括瞬时卸荷变形和时效变形[16−18]。为了全面反映千枚岩的蠕变及损伤演化的过程,本文参照此前研究[19]所提方法,在Burgers 模型的基础上,串联黏塑性元件(Bingham体)和加载塑性元件(莫尔库仑体),如图8所示。

图8 自定义蠕变模型Fig.8 User-defined rheological model
由于茂县隧道F1断层处的岩体内部节理发育,并广泛分布震裂损伤,根据岩石力学相关内容[20],通过切割度反映岩体的损伤程度。设岩体的体积为V,x方向上各节理平均距离为L,第i个节理面的面积为ai,则x方向上的切割度Xx为

同理可得岩体在y方向和z方向上的切割度Xy和Xz,定义岩体总损伤张量X为

物体的总体应变可分解为应变球张量和应变偏张量。其中应变偏张量反映了物体形状的变化,黏塑性偏应变引起的物体几何形状的改变是导致损伤发展的原因。以z方向上的节理平面为例,应变偏张量对节理损伤演化的影响如图9所示。

图9 损伤演化原理Fig.9 Principle of damage revolution
z方向上的切割度增量dXz可表示为节理面积改变量与平面面积之比,如式(3)所示,更新后的损伤变为

式中:e为偏应变。
岩体裂隙不能传递全部压应力和剪应力,定义传压系数Cn和传剪系数Cs。考虑损伤演化的本构方程为:

式中:为有效应力张量;Slk为偏应力张量;I为单位二阶张量;σm为球应力张量;H(*)为判别式,当球应力张量取不同数值时,该数值直接判别为0 或1;δij为柯西符号张量,当σm>0 时,H(σm)=1,当σm≤0时,H(σm)=0。
在数值计算过程中,根据实际应力求得反映岩体损伤的有效应力,将有效应力代入蠕变本构模型中计算岩体的黏弹塑性变形,更新岩体的损伤加以储存,并不断进行迭代计算,即可在FLAC3D中实现岩体的蠕变损伤演化计算。
3.2 数值模型的建立
图10所示为通过FLAC3D创建的茂县隧道计算模型。为了消除边界对计算结果造成的误差,将模型的长×宽×高设为120 m×120 m×3 m,使隧道外轮廓与边界的距离比5倍洞径大。对模型的底部和四周边界进行约束,令其不产生垂直于边界的位移,并根据隧道埋深施加自重应力场。隧道采用钢拱架锚喷联合支护形式。其中,初期支护厚28 cm,为C25喷射混凝土;钢拱架为H175型钢间距为0.6 m,钢拱架的支护作用通过提升初期支护整体刚度进行等效;砂浆锚杆的长度为4.5 m,环向间距为1.2 m,纵向间距为0.8 m。二次衬砌为C35 模筑钢筋混凝土,厚度为60 cm。支护结构的物理力学参数如表1所示。
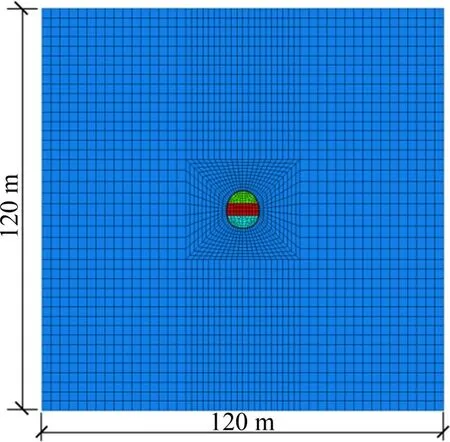
图10 茂县隧道数值模型Fig.10 Numerical model of Maoxian tunnel

表1 隧道支护结构的物理力学参数Table 1 Physical and mechanical parameters of supporting structures
在数值模拟过程中,锚杆采用cable单元模拟,二次衬砌采用shell 单元模拟,围岩和初期支护为实体单元。为了简化计算,假设初期支护和二次衬砌的应力、应变满足弹塑性本构关系,围岩的应力、应变关系符合自定义的蠕变损伤本构模型。
陡倾岩体隧道,左右拱腰的变形较大[21],茂县隧道周边为陡倾千枚岩,围岩的节理面垂直于数值模型的x轴,因此,在计算中开启x方向的蠕变损伤。
3.3 蠕变参数反演
获得符合工程实际的计算参数是进行数值计算研究的前提,茂县隧道F1 断层处斜井的断面形式与开挖工法和正洞相同,仅施作一层锚喷支护,其埋深约为409.6 m。依据李磊等[22]所得茂县隧道1号斜井XJ1K0+570 处的千枚岩位移监测结果,将遗传算法(GA)的思想引入粒子群算法(PSO)[23−24],反演本构模型中和蠕变有关的参数。破碎千枚岩岩体的物理力学参数由室内试验确定,如表2所示。

表2 破碎千枚岩岩体的物理力学参数Table 2 Physical and mechanical properties of broken phyllite
粒子群算法是一种模仿鸟类群聚行为的智能算法[25],在算法中单个粒子称为“个体”,粒子的集合称为“种群”。在迭代过程中,各粒子的位置和速度根据下式进行调整,迭代求出最优解:

式中:vin和Xin分别为第n次迭代中第i个粒子的速度和位置;w为惯性权重;c1和c2为学习因子;r1和r2为(0,1)上的随机数;pbestni和gbestn分别为个体最优值和全局最优值,根据适应度函数f(x)判断。本文的f(x)为计算结果u(x)和实测围岩位移u误差的二范数:

为了避免粒子群算法后期出现陷入局部最优的情况,在算法中引入变异的概念,改进后的GA-PSO算法的具体步骤如下。
1)在Matlab 中设置初始种群中各粒子的随机位置和速度,粒子的位置X=(Ek,ηk,Em,ηm,ηB),并将参数导出为符合FLAC3D格式的赋值命令流。
2)调用有限差分软件FLAC3D进行数值模拟,设定蠕变计算时间为400 d,记录茂县隧道1 号斜井拱顶和拱腰处的位移和相应的蠕变时间,并计算每个粒子对应的适应度。
3)更新记录个体极值pbestni和全局极值gbestn的矩阵,根据粒子群算法的计算原则更新各粒子的速度和位置,并对更新后的粒子执行变异操作;重复上述迭代过程,直到计算误差满足精度要求为止。
图11所示为1 号斜井拱顶、拱腰位移计算曲线与实测位移曲线的对比。由图11可知:计算结果和现场实测结果较吻合,反演出的参数能较好地反映破碎千枚岩岩体的工程特性。千枚岩的蠕变参数如表3所示。

图11 计算结果与实测结果对比Fig.11 Comparison of numerical and measured results

表3 破碎千枚岩岩体的蠕变参数Table 3 Creep parameters of broken phyllite
4 计算结果分析
将斜井变形数据反演得出的F1 断层千枚岩蠕变参数应用到茂县隧道正洞开挖计算过程中。应力解除法测得正洞试验段K127+936断面拱腰位置的竖向应力σV为12.7 MPa,最大、最小水平主应力σH和σh分别为21.4 MPa和15.1 MPa。将初始地应力场施加到数值模型上,利用蠕变损伤演化模型计算F1 断层正洞施工期,单层初期支护和双层初期支护断面,围岩的位移、二次衬砌内力和岩体内部损伤随时间的演化规律。
4.1 围岩位移分析
图12所示为分别采用单层初期支护和双层初期支护工法的F1 断层正洞断面,周边岩体测点位移随时间的变化曲线。图中拱肩、拱腰和拱脚处围岩的水平收敛以及拱顶沉降均设为正值。

图12 隧道周边围岩位移Fig.12 Deformation of surrounding rock
由12 图可知:开挖后围岩各测点处的位移迅速增加,在第一层初期支护施作后的25 d 内,各测点处围岩位移的平均增长速率约为4.03 mm/d,其中拱腰位置的收敛值增长最快,拱顶沉降的增长速率最慢。对于采用单层初期支护工法的断面,隧道周边围岩各测点位移的增长率直到二次衬砌施作后才显著下降,但围岩的变形仍缓慢增长,平均增长率约为0.30 mm/d。在二次衬砌施作后,围岩的变形并未达到稳定。在断面开挖300 d后,拱腰收敛的位移为0.28 m,拱顶沉降的位移为0.16 m。
对于采用双层初期支护工法的断面,第二层初期支护施作后,围岩各测点的位移增长率的平均值降低至0.71 mm/d,且位移的变化逐渐趋于稳定。在二次衬砌施作后隧道周边围岩的位移几乎不再增加,平均增长率仅为0.04 mm/d。开挖300 d后,拱腰收敛位移为0.14 m,拱顶沉降的位移为0.09 m,相比于单层初期支护工法分别降低了45.4%和49.9%。由此可见,采用双层初期支护工法能够有效地控制隧道周边围岩的变形。
4.2 二次衬砌内力分析
4.2.1 采用单层初期支护工法的内力
二次衬砌的内力是反映隧道长期安全的重要指标,图13所示为采用单层初期支护时,二次衬砌轴力和弯矩的现场监测及数值计算结果随时间的演化曲线。其中,轴力以二次衬砌混凝土截面受压为正,弯矩以支护结构内侧受拉为正。

图13 单层初期支护的二次衬砌内力图Fig.13 Internal force of the secondary lining with single primary support method
与普通围岩隧道相比,高地应力软岩隧道的内力较大。由图13可知:采用单层初期支护工法的断面,二次衬砌轴力在施工75 d 内迅速增大;受围岩蠕变效应的影响,在二衬施作后的240 d内,轴力并未达到稳定;最大轴力出现在拱顶位置,为8 610.9 kN,最小轴力出现在拱腰位置,为5 192.6 kN;二次衬砌弯矩随时间的变化趋势与轴力演化规律类似;受陡倾层状岩体水平挤压作用的影响,最大正弯矩位于拱腰位置,监测240 d时,为527.9 kN·m;最大负弯矩出现在拱顶位置,为−294.3 kN·m。
与未考虑围岩损伤的拱顶和拱腰轴力演化曲线相比,考虑损伤的拱顶轴力的数值计算结果与实测结果更为接近。在二次衬砌施作240 d时,前者计算出的拱顶、拱腰轴力分别为7 427.1 kN和4 508.7 kN,后者计算出的拱顶、拱腰轴力分别为8 987.6 kN和5 275.4 kN。
4.2.2 采用双层初期支护工法的内力
图14所示为采用双层初期支护工法时,二次衬砌轴力和弯矩的现场监测及数值计算结果随时间的演化曲线。
由图14可知:采用双层初期支护工法的断面,二次衬砌轴力与单层初期支护相比显著降低;在二次衬砌施工后的第240天,拱顶和拱腰处的轴力分别为4 635.54 kN和2 830.23 kN,各测点轴力的平均值降低了47.4%。二次衬砌施作75 d后,轴力的增长率迅速降低,并在250 d 内逐渐趋于稳定,围岩的蠕变效应得到了有效控制。最大正弯矩位于拱腰位置,为331.31 kN·m,最大负弯矩位于拱顶位置,为−216.27 kN·m,与采用单层初期支护工法的断面相比各测点的平均弯矩降低了31.9%。

图14 双层初期支护的二次衬砌内力图Fig.14 Internal force of the secondary lining with double primary support method
对于采用双层初期支护工法的断面,二次衬砌施作240 d 时,未考虑损伤的拱顶、拱腰处轴力的计算结果分别为3 778.5 kN和2 643.2 kN,考虑损伤的拱顶、拱腰处轴力计算结果分别为4 727.6 kN和3 195.8 kN,考虑损伤时轴力计算结果的平均值增长了23.0%。
数值模拟结果表明,计算初期蠕变损伤模型的计算结果与实测结果相比偏小。这可能是由于除了x方向外,围岩的y和z方向也存在一定的损伤,而在计算过程中仅考虑了x方向的损伤。与不考虑损伤的蠕变本构模型相比,蠕变损伤演化模型能够更好地反映高地应力层状陡倾千枚岩隧道的力学特征。传统的计算方法会导致最终的计算结果偏小,从而影响隧道支护结构的安全设计。隧道最危险截面位于拱腰,采用单层初期支护工法和双层初期支护工法的断面,拱腰混凝土截面的安全系数分别为1.57和3.13,前者处于较危险的状态。
4.3 围岩内部损伤
在计算完成后,反映岩体损伤的指标Xs将作为特征值存储在模型的实体单元中,可以通过自定义命令“z_prop(pnt,’damage’)”等提取各实体单元中围岩的损伤结果和位置坐标。开挖300 d后,隧道周边围岩的损伤演化云图如图15所示。
由图15可知:陡倾层状千枚岩岩体的损伤主要集中在拱腰位置,拱顶和仰拱处的损伤发展相对缓慢,这会导致拱腰处首先发生钢拱架扭曲和二次衬砌开裂等病害,与现场观测的结果相符。开挖300 d 时,围岩的最大损伤均贴近拱腰外侧,其数值分别为0.18和0.34。采用双层初期支护工法的断面围岩损伤最大值减少了47.1%,这表明双层初期支护工法有效地降低了围岩内部损伤积累演化的速度,提高了隧道施工和运营阶段的安全性能。

图15 隧道周边围岩损伤演化示意图Fig.15 Schematic diagrams of processes of damage evolution growth in surrounding rock
此外,采用单层初期支护工法时,围岩损伤受隧道开挖影响的范围显著增加,在水平方向上损伤增长区域的宽度为24.5 m,面积为222.1 m2。而采用双层初期支护工法时,损伤增长区域的宽度为19.6 m,面积为162.9 m2,与采用单层初期支护方法相比,横向宽度和面积分别减小了20.0%和26.7%。从形状上看,采用双层初期支护工法时,围岩损伤增长区域在隧道洞周的分布更加均匀,这有利于避免隧道周边围岩在某处提前发生屈服破坏,从而提升了围岩整体自承能力。计算结果表明,双层初期支护具有的分步让压特性和更高的支护刚度有效地限制了围岩变形,减小了塑性和黏性变形占围岩总体变形的比例,从而控制了围岩损伤和后期蠕变的发展,提升了支护结构在运营期的稳定性。
4.4 双层初期支护的承载机理
图16所示为采用及时强支护措施和分层支护措施时的围岩−支护特征曲线。当采用及时强支护措施时,支护结构的整体刚度很高,可以将围岩的变形控制在较低的水平(位移d1),但是围岩变形产生的压力几乎全部由支护结构承担(支护力s1)。考虑围岩的流变效应,隧道运营期间支护结构承担的围岩荷载将持续增加,现有的施工材料很难满足强支护方案的强度要求,采用及时强支护的施工方法往往不能取得预期的效果。双层初期支护工法施加的第一层初期支护为锚喷柔性支护和强支护措施相比刚度较低,围岩可以通过变形释放部分压力。在隧道周边围岩和衬砌结构破坏之前(曲线ACD),施加第二层初期支护,加强支护系统整体的刚度和强度,将围岩内部的损伤控制在一个较低的水平,使围岩和支护体系可以在E点达到新的平衡状态。此时围岩的变形位移为d2,支护应力为s2,围岩内部应力显著降低,支护结构的安全储备有所提升。因此,分层支护工法对具有显著蠕变效应的高地应软岩隧道具有较好的适应性。

图16 双层初期支护的承载机理Fig.16 Mechanism of double primary support method
5 结论
1)高地应力陡倾层状软岩隧道主要受到水平挤压作用,支护结构承受的最大围岩压力位于拱腰位置,采用双层初期支护工法的断面所受围岩压力较低,能在更短的时间内达到稳定状态。此外,隧道二次衬砌承担的荷载比例显著降低,提高了隧道支护结构在隧道运营期的安全储备。
2)采用GA-PSO 算法,通过软件间的互相调用,可以充分利用不同软件的优势处理复杂的工程问题。基于茂县隧道F1 断层破碎带斜井处的位移监测数据,通过对计算结果多次迭代,能够有效地逼近各参数在定义域范围内的最优解。自定义的黏−弹塑性蠕变损伤演化本构模型能够较好地反映高地应力场中陡倾层状千枚岩岩体的变形特性。
3)隧道的最大变形位于拱腰位置,拱顶的变形最小,隧道的最大正弯矩和最大负弯矩分别位于拱腰和拱顶处。采用双层初期支护工法能够显著减小隧道周边围岩的变形和二次衬砌内部的轴力和弯矩,缩短变形和内力增长的时间,使其在较短的时间内达到相对稳定状态。
4)隧道周边岩体的损伤主要集中在拱腰位置,拱顶和仰拱处的损伤发展相对缓慢。当采用双层初期支护工法时,隧道周边岩体内部的损伤分布更加均匀,与单层初期支护工法相比,围岩内部损伤的最大值和分布区域的面积分别降低了47.1%和26.7%,有利于提高隧道周边围岩的强度,发挥其自承能力,从而减缓隧道长期蠕变的发展进程。

