深部矿井频繁微扰动下煤巷损伤累积演化规律

魏明尧，刘春，刘应科，满忠毅，王强，牛宏伟

(1.中国矿业大学矿山互联网应用技术国家地方联合工程实验室，江苏徐州，221116；2.中国矿业大学江苏省城市地下空间火灾防护高校重点实验室，江苏徐州，221116；3.潞安化工集团有限公司，山西长治，046200)

煤矿井下围岩体受采动影响产生变形、破断等现象，对采矿矿井、地表建筑和环境具有重大影响。冲击地压是围岩体在高应力环境下的局部失稳，轻则造成了矿井巷道变形、支护失效、片帮冒顶、设备损坏等，重则造成重大人员伤亡和地面建筑物严重破坏等事故[1]。冲击地压灾害是预测和治理难度最大的灾害之一，对深部煤炭资源的高效、安全开采造成巨大威胁。随着地下矿山开采深度的增加，冲击地压对矿业生产的威胁有日益严重的趋势。因此，对冲击地压灾害的诱发机制和对围岩的破坏过程的研究十分迫切。

从力学的观点来看，冲击地压与巷道围岩的应力状态、岩性及周围的动力扰动等因素有关，其发生过程是煤岩体在多种因素作用下的瞬间失稳破裂过程[2]。在深部煤层开采中，爆破、机械振动、水力压裂、相邻岩爆产生的应力波、顶板断裂和地震波等动态应力都可能成为触发冲击破坏的诱因[3]。对于深部的煤岩体，由于巷道周边的应力集中更加明显，故动态扰动对于岩爆的触发作用也更加突出。许强等[4]认为当地质体的演化处于临界稳定状态时，微小的扰动便可以诱发地质灾害的发生；当地质体的演化仅处于接近临界稳定状态时，强烈的扰动也可以诱发地质灾害提前发生。谢勇谋等[5]分析了开挖爆破产生的应力波在围岩中的传播及对围岩的影响，爆破产生的横波和纵波分别在围岩中形成垂直和平行围岩表面的张拉破裂面，它们为冲击地压的发生提供了物质基础。在数值模拟方面，秦昊等[6]采用非连续离散元软件UDEC 对应力波扰动诱发冲击矿压形成发生全过程、巷道埋深及扰动应力强度对围岩稳定性的影响进行了数值模拟，得到了巷道围岩在应力波扰动过程中响应速率、响应变形及岩体破损范围，以及发生冲击矿压的临界深度和临界扰动应力强度。左宇军等[7]采用动态版岩石破裂过程分析系统RFPA2D分析了动力扰动对深部岩巷破坏过程的影响，从细观角度分析了不同深度或受不同静压力的岩石巷道在动力扰动下的破坏规律。ZHU等[8]采用RFPA2D 软件模拟了不同侧压力系数和不同扰动波形条件下动态扰动触发深部巷道发生失稳破裂的整个过程，并揭示动态扰动触发巷道岩爆的力学机制。陈建功等[9]研究了深部洞室围岩分区破裂化的冲击破坏机制，认为岩体开挖引起围岩径向应力产生了间断面，当此间断面压力差满足产生冲击波条件时，即产生局部冲击破坏。雷光宇等[10]采用LS-DYNA 软件对扰动应力波作用下巷帮围岩层裂破坏结构的形成过程、扰动应力波强度对层裂结构形成的影响进行了有效的数值模拟，得到了一定巷道围岩应力状态下巷帮围岩层裂结构的形状、厚度等特征。余伟健等[11]理论分析了掘进爆破扰动应力传播规律及其影响，认为爆破扰动次数越多，邻近巷道围岩变形越严重。宫凤强等[12−13]研究了预静载条件下硬岩受动力扰动的断裂特性变化规律，结果表明高频扰动有利于岩石的断裂破坏，而且冲击强度与应变率指数相关。LI等[14]分析了动静加载的能量释放机理，认为静载应力是影响岩石破坏形式的主要因素，外部动力扰动是重要的诱因。试验方面，尹光志等[15]进行了动态往复加载的层状复合煤岩体的破坏试验，发现扰动型复合动力灾害发生时的破坏程度和抛射动能均明显大于高静载型复合动力灾害。刘涛等[16]试验研究了高应力条件下受低频循环扰动条件下的力学特性，发现高应力的循环扰动造成复杂的破坏形态。王春等[17−18]进行了一维高静载频繁动态扰动试验，研究了弹塑性能、反射能、透射能与扰动冲击次数的关系，发现冲击扰动过程中岩石处于释放能量的状态。唐礼忠等[19]采用改进的SHPB动静加载装置，测试了频繁动力扰动对高储能岩体动力学响应，发现在低轴压下动态峰值应力和弹性模量随着动力扰动次数增加先升高后降低，较高轴压时均表现为下降。现场实测中，陈亚楠等[20]采用地质雷达测得了多次爆破振动下围岩松动圈逐渐增大，距离爆破点远区影响很小。孙金山等[21−22]采用声波测试了爆破后巷道围岩波速，结果表明，随着爆破次数的增加，巷道围岩逐步发生松动劣化，损伤逐步累积，呈非线性趋势增长。

虽然目前对动力扰动下的煤岩体损伤研究较多，但对于低强度的频繁扰动研究较少，尤其是缺少频繁扰动影响下的深部围岩稳定性研究。本文作者将岩石视为非均匀介质，并考虑煤岩体损伤和峰后应变软化特性，采用FLAC3D 软件动力计算模块，对多次动态扰动下深部巷道的变形与破裂过程进行数值模拟，分析煤层动力扰动致使裂隙发展过程以及损伤区的演化规律，并就扰动频次和埋深因素对围岩破坏的影响进行深入分析，探讨频繁动力扰动下围岩损伤破坏以及诱发围岩大范围破坏的过程，能够对动力扰动严重的巷道开挖和支护提供指导。

1 煤体损伤本构模型及应变软化特征

煤岩体的变形响应是由外界荷载决定的。在外部荷载小于一定值时，煤岩体应变与应力为线弹性关系；当荷载超过弹性极限，应力−应变关系则不再是理想弹性状态，即煤岩体某些部分的应力状态逐渐进入塑性状态。在小变形假设条件下，含瓦斯煤岩的总应变εij同样可以表示为弹性应变与塑性应变的总和：

考虑塑性应变的理想弹塑性本构关系可以写为

式中：σij为应力张量；Eijkl为材料的弹性刚度张量；εij和分别为应变张量和塑性应变张量。煤岩体的损伤主要是由微裂纹的萌生和扩展引起的，这些微裂隙发展会导致的煤岩体的体积膨胀，因此可以用弹性体积应变及塑性体积应变表征岩石的损伤增量，采用如下损伤演化方程[23]：

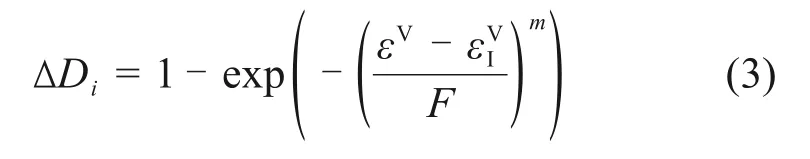
式中：ΔDi为第i次动力扰动产生的损伤增量；εV为动力扰动产生的最大体积应变；εVI为体积应变损伤阀值，即体积应变达到阀值时才开始产生损伤，反映了岩体损伤的合理初始损伤起点问题[24]；F为煤体强度参数，反映了煤体宏观统计平均强度大小；m为常数，反映了煤体强度分布的集中程度。建立的损伤演化方程是标量形式的损伤增量，把单元体内损伤均匀化处理，减小了计算量。

重复动力扰动作用下导致围岩损伤的累积，由单次扰动产生的损伤增量叠加表示，建立了多次扰动下的增量型损伤演化方程为：

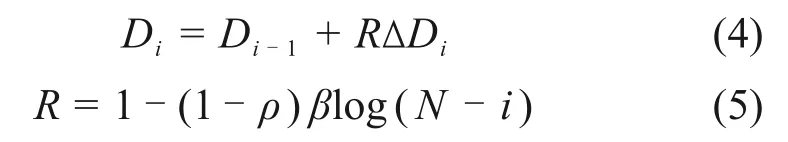
式中：R为名义应力比；ρ和β为材料疲劳寿命常数；N为疲劳寿命。R代表了不同扰动荷载次数下的损伤累积系数，随着扰动次数的增加，样品实际承载能力下降，单次造成的损伤增量增加[25]。

基于Lemaitre应变等价性假说[26]，损伤对应变行为的影响通过有效应力来体现，因此可以建立煤岩体损伤本构关系如下：

理想弹塑性材料屈服后就开始产生塑性流动，变形无限制的发展，直至破坏。这种过程不存在强化效应，在加载状态时，理想弹塑性材料屈服面的形状、大小和位置都是固定的，而强化材料在加载过程中，随着应力状态和加载路径的变化，后继屈服面(也称为加载曲面)的形状、大小和中心的位置都可能发生变化[27]。煤岩体等强化材料在加载过程中，当内变量改变时，屈服面也将随之发生变化，不同的内变量对应着不同的后继屈服面。在目前广泛使用的强度准则中，基本强度参数是材料的黏聚力和摩擦因数。岩石试件在试验加载的过程中，一定会经历应变软化的过程。大量的室内试验和现场测试结果表明[28]，在应变软化的过程中，岩石的强度参数会发生变化。因此，采用塑性应变进行煤体材料黏聚力软化，表征黏聚力随塑性应变增加的变化过程。从力学观点看，脆性材料失效的过程就是材料颗粒间黏结强度的降低，黏结强度会随着岩体的裂隙错动和剪切形成新的裂隙而逐渐降低[29]。因此，煤体材料的黏聚力和塑性应变密切相关。根据实验结论，HAJIABDOLMAJID[30]建立了如下的黏聚力软化模型：

式中：c0为初始黏聚力；cr为残余黏聚力；εP为有效塑性应变参数；εPc为黏结强度。有效塑性应变εP和裂隙的扩展过程有关，决定了目前和历史的裂隙情况，表达式为

式中：dεP1，dεP2和dεP3分别为第一、第二和第三主塑性应变增量。

当材料受到超过其强度的压力时，会发生失效而失去承载能力，脆性材料的失效一般表现为断裂。一般煤岩体的压缩强度要远大于剪切强度和拉伸强度，因此，岩体的破坏多是以剪切和拉伸破坏形式为主。煤岩体发生破坏后即进入塑性变形阶段，流动法则给出了塑性应变增量的方向和大小，因此采用流动法则描述煤岩体的非线性塑性特征。本文模拟时采用Mohr-Coulomb 计算模型[31]，计算过程中分别对发生剪切和拉伸破坏单元进行相应的应变量塑性修正。

裂隙煤体抗剪强度一般采用Mohr-Coulomb 准则，剪切破坏准则基本形式为[31]：

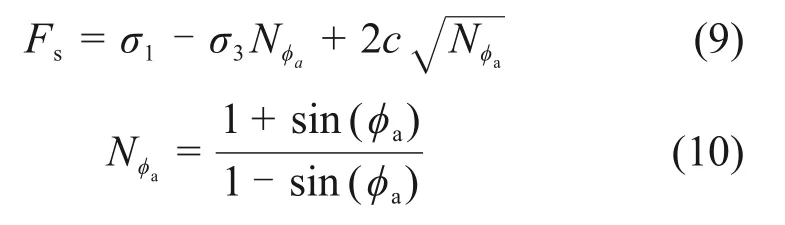
式中：Fs为剪切破坏包络线；σ1和σ3分别为最大主应力和最小主应力，MPa；φa为摩擦角，(°)；c为黏聚力，MPa。

拉伸破坏准则为：

式中：Ft为拉伸破坏包络线；σt为抗拉强度，MPa。

建立的屈服函数代表了在有效应力空间内的一个空间曲面，它决定了材料失效的状态，即判断单元的应力状态，Fs小于0时，认为此单元发生剪切破坏，Ft大于0时，认为此单元拉伸破坏。

以上建立的破坏准则可以有效判定单元的破坏类型，对于破坏后的单元采用非关联流动法则进行塑性修正[31−32]，并进行相应的应变塑性修正，同时考虑了损伤影响下的有效应力变化，从而得到合理的应力。

2 数值计算模型

为了通过数值方法求解损伤本构模型，基于采用FLAC3D 软件的本构自定义功能加入损伤本构模型。FLAC3D程序能够准确地模拟材料的塑性破坏和流动。FLAC3D的二次开发环境提供了开放用户的接口，自带的uDM 工具可以提供一般情况下的模型修改与开发。自定义本构模型开发采用C++语言，且编译成DLL文件(动态链接库)，动态链接库文件能在需要的时候随时加载上去。对于自定义本构模型的编写主要工作是修改头文件(.H)文件和程序文件(.CPP)[33]。在头文件中进行新的本构模型派生类的声明，修改模型的ID、名称和版本，修改派生类的私有成员，包括模型的基本参数及程序执行过程中主要的中间变量。在程序文件中需要进行的修改有以下几个方面：1)修改模型结构(UserModel::UserModel(bool bRegister):Constitutive Model)给头文件中定义的所有私有成员赋初值；2)修改UserModel::Properties( )函数字符串进行模型参数赋值；3)修改UserModel::States()函数进行计算过程中的状态指示；4)按照派生类中定义的模型参数变量修改UserModel::GetProperty( )和UserModel::SetProperty( )函数；5)修改UserModel::Initialize()函数执行参数和状态指示器的初始化，并对派生类声明中定义的私有变量进行赋值；6)根据单元应力情况对单元状态指示器进行修改UserModel::Run( )；7)修改UserModel::SaveRestore( )对计算结果进行保存；8)在程序文件中加入return()语句调试程序。

采用VC++2005软件编写了累积损伤本构模型的动态链接库文件Damage_model.dll，损伤本构模型的计算流程如图1所示。通过C++语言编译程序生成本构模型的dll 文件，在FLAC3D 程序中必须使用CONFIG cppudm 命令设置配置以接受dll 模型。然后模型的dll文件通过命令“MODEL LOAD Damage_model.dll”运行时被载入，此后FLAC3D程序和FISH都能够识别模型及其特征名。

图1 损伤本构模型计算流程Fig.1 Flow chart of computation process for damage constitutive model

3 循环快速加载实验测试

循环动力扰动能够引起煤体微裂隙的开裂和扩展，为研究频繁微扰动引起的煤体损伤规律，进行了煤样在循环扰动下的实验测试，采用的实验设备如图2所示。煤样采自山西长治李村煤矿，煤品为贫煤，样品为直径5 cm、高10 cm 的圆柱体。首先把样品装入橡胶套内，前后端分别安装好轴向端头，采用高压柱塞泵进行环向围压的加载。由于柱塞泵的加载速度慢，无法实现快速加载，故轴压方向采用气体压力控制阀进行气体脉冲加载，实验过程环压保持3 MPa不变，轴压采用3 MPa—1 MPa—3 MPa 的循环加卸载，每个循环间隔为1 s。此时，静载状态下的轴压要小于抗压强度，外部动载为样品损伤的主要因素。由于无法直接测量和评估循环加载对样品造成的损伤程度，采用样品的渗透率间接反映损伤规律。在实验开始后，首先采用脉冲衰减法测定样品渗透率，然后采用气体压力脉冲对轴压进行加卸载，每500次加载循环后测量一次渗透率。

图2 循环加载设备示意图Fig.2 Schematic of cyclic loading equipment

为了验证新建立模型的准确性，采用FLAC3D软件对循环加卸载实验进行了数值模拟，得到不同加卸载次数与损伤的关系，然后根据损伤与渗透率的关系[34]得到渗透率变化规律，并与实验数据进行对比分析，如图3所示。模拟选取的煤体体积模量为5 GPa，剪切模量为3 GPa，黏聚力为4.5 MPa，抗拉强度为1 MPa，剪胀角为5°，密度为1 500 kg/m3。样品加载前，渗透率为0.04×10−3μm2，在加载次数为500时，渗透率降低至0.022×10−3μm2，这是由于动力扰动造成轴向煤颗粒间密实，降低了渗透性能。随着加载次数增加，渗透率逐渐上升，当加载到2 000次时，渗透率增加到了初始值的7倍。数值模拟计算得到的煤体损伤随加载次数增加而缓慢上升，每次加载扰动造成样品的损伤逐渐累积。造成单个测试点的渗透率和模拟结果不一致的原因：一方面为压力传感器和压力控制器的精度产生的渗透率测量误差，另一方面冲击破坏产生的煤粉也影响测试结果。但是，渗透率与加载次数的变化趋势与模拟结果一致，单个实验测试点不影响整体规律。通过损伤与渗透率的关系模型计算得到的相应渗透率变化趋势与实验结果基本一致，基本呈指数增加，即扰动较少时对渗透率影响较小，随着加载次数增加造成渗透率升高幅度也增加。由此可以证明，建立的力学模型能够反映煤体在外部循环扰动下的损伤演化规律。

图3 煤样渗透率与循环加载次数的关系Fig.3 Relationship between coal permeability and number of cyclic loading

循环加载2 000次后，将样品卸压，取出后的样品及表面微观显微照片如图4所示。从图4可以发现：样品产生2处断裂面，垂直样品轴向产生裂纹较多，且角度基本为90°，且断裂面较完整(图4(b))；多次加载卸载产生拉伸裂纹，裂纹面光滑，且能看到镜质体上的翼状拉伸裂纹(图4(d))，表明循环加载造成轴向的拉应力叠加，超过煤体拉伸强度后产生拉伸破裂面。由于新生破裂面垂直于流体流动方向，因此，拉伸破坏对渗透率的影响较小。

图4 煤样表面微观显微照片Fig.4 Micrographs of coal surface

4 频繁微扰动对围岩损伤破坏规律

以某矿区的采矿地质条件为背景，选取巷道断面作为计算实例。该处煤层巷道埋深600 m，水平地应力约为垂直地应力的1.3倍。为减少模型尺寸，简化模型结构，节约计算时间，可以视巷道围岩为平面应变问题，同时假设整个模型中煤层厚度很大，忽略了支护结构和岩层的影响。计算模型的长×宽为24 m×24 m，巷道几何形状为拱形，宽度为4 m，最大高度4 m，计算区域总共划分为2 200个6面体单元，如图5所示。设置模型两侧边界和底边界为垂直边界方向的链杆约束，在上边界为覆岩作用于该边界的分布载荷。模拟时先进行地应力平衡，对巷道开挖，然后进行计算应力重新分布的过程。

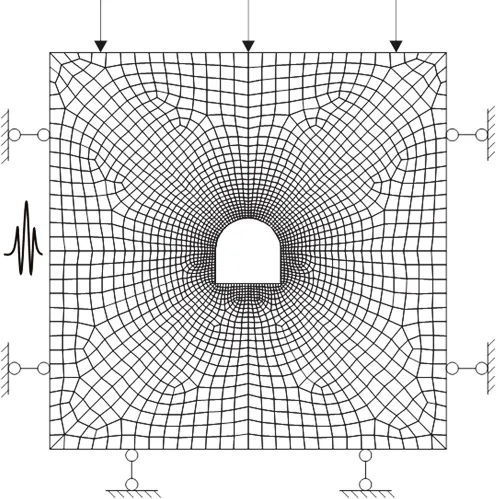
图5 模型及边界条件示意图Fig.5 Schematic diagram of numerical simulation model

煤岩体具有非均质特性，因此假定单元的力学参数服从Gauss分布，煤岩体的力学参数的平均值如表1所示[35]，标准方差均为5%。其他参数如表2所示，围岩力学参数取自矿区资料和相关文献。

表1 煤岩体的Gauss分布参数[35]Table 1 Gauss distribution of parameters for coal

表2 模型中煤体力学场参数Table 2 Modeling parameters for numerical simulation

采用微震监测仪对井下开采导致的顶板断裂震源进行了数据监测采集，现场监测施工过程受场地限制，选择了距离震源200 m 处设置传感器，此位置完全能够获得准确的微震信号，而且能够避免工作面的信号干扰。为了模拟顶板断裂产生的外界动力扰动对巷道的作用机理，模型中将得到质点振动速度数据作为模型的扰动源(图6)，在FLAC3D中通过在左侧边界施加位移应力波，并按不同扰动次数施加动载。模型力学阻尼选用瑞利阻尼形式，其中最小临界阻尼比为0.005，最小中心频率为25 Hz，边界条件设置为静态边界[36]。

4.1 频繁动力扰动造成的围岩破裂特征

巷道掘进后对围岩应力场产生影响，造成应力重新分布。而动力扰动应力波在巷道围岩的应力分布上进行叠加，增大了围岩应力，进一步加剧了围岩的变形和破坏。图7所示为频繁动力扰动后巷道围岩的变形情况，动力扰动次数为100 次。从图7可以看出：巷道围岩受应力波扰动发生变形，其中，巷道左帮围岩受扰动影响最大，产生较大位移，并在约离左帮0.5 m范围内的围岩发生严重的变形破坏。而巷道右侧由于受扰动影响较弱，产生的变形量小。同时，顶底板也产生较大变形量，底板中部向上鼓起，顶板偏左部也产生了较大下沉。

图7 巷道围岩位移示意图Fig.7 Schematic diagram of displacement

动力扰动造成围岩破坏，同时还引起煤体损伤发展。当发生塑性变形时，岩土类材料产生的一个重要特征是剪胀效应，即外部剪切作用下导致材料体积膨胀。图8所示为多次动力扰动后围岩的损伤规律示意图。从图8可以看出：围岩内存在多条贯通的损伤破坏区。由于动力扰动源位于巷道左侧，因此，在左侧底脚处，围岩的损伤最大，说明此处煤体破碎严重。沿着左右底脚，在底板形成连接的损伤带，同时，在顶板也存在类似损伤带，这说明较大的水平应力造成顶底板位置破坏严重。在左侧围岩内，受动力扰动作用，距离左帮约2 m处形成一条上下贯通的损伤带。在动态扰动过程中巷道左帮围岩变形破坏，形成贯通的损伤带，随着扰动次数的增加，造成围岩破坏加剧，形成多条贯通的损伤带，极易发生瞬间失稳，形成片帮甚至围岩的冲击破坏。同时，围岩大范围进入塑性状态，尤其受动力扰动影响强烈的左侧围岩。在远离巷道顶部、底部和左帮的围岩多为剪切破坏，靠近巷道左帮附近围岩和巷道底板为拉伸破坏。由于扰动应力波在巷道壁面发生反射，造成左帮围岩内破坏形式复杂，煤体破坏严重。

图8 巷道围岩损伤示意图Fig.8 Schematic diagram of damage

4.2 扰动次数对围岩破坏的影响

煤层围岩受微动力扰动导致微裂纹的萌生和扩展，而多次的扰动将导致损伤的逐渐累积，微裂纹贯通形成宏观裂纹，致使围岩损伤程度和损伤范围的增加。图9所示为不同扰动次数下的围岩损伤情况。从图9可以看出：在未受到动力扰动时，巷道掘进导致应力的重新分布，围岩产生拉伸或剪切破坏，进入塑性损伤状态，距离巷道越近损伤程度越高。巷道底帮破损较严重，底板损伤造成底鼓。当巷道遭受扰动次数为20 次时，造成巷道左侧围岩损伤程度明显增加，损伤范围也增加。同时，左侧底部的损伤区域向内部延伸。随着扰动次数的增加，围岩整体损伤程度和范围都增加，而损伤破坏带继续向围岩内部延伸，底板下部损伤程度也进一步加剧。当扰动次数达到60 次时，损伤区域更加集中，而且损伤程度明显大于其他区域损伤程度。当扰动次数达到100 次时，损伤带贯通，围岩内部形成多条带状破坏区，而巷道壁面位置损伤程度较小。因此，扰动次数超过临界点后，围岩损伤程度大幅增加，形成贯通的损伤带，易引起围岩区域性的严重破坏。当扰动次数继续增加，在左帮和顶底板出现大面积损伤区，呈现区域性损伤破坏，并且贯通的损伤破坏区整体向巷道内变形。

图9 动力扰动次数对巷道损伤增量的影响(箭头方向代表单元体位移矢量)Fig.9 Effect of numbers of disturbance on damage increment

动力扰动造成围岩损伤的增加，图10所示为模型中不同测点损伤增量与扰动次数的关系，监测点1 位置位于巷道左侧，距离壁面2.5 m，监测点2位于距离底板2.5 m处。从图10可以看出：随着扰动次数的增加，围岩损伤程度呈增加趋势，且损伤增幅增加，在200次扰动时，围岩损伤增加50%。不同测点对扰动次数的响应也不同，在扰动次数较少时，底板测点的损伤增量小于左侧围岩的损伤增量，随着扰动次数增加，底板位置损伤程度显著增加。由于井下真实环境中扰动源复杂，对围岩的损伤难以定量测定，本文与徐世达等[37]进行的爆破震动后围岩钻孔声波实测数据(如图11所示)进行对比分析。由于爆破产生扰动强度大，对围岩损伤程度高，仅测得6 次扰动后围岩损伤量。选取的3 个声波测孔孔口距离巷道底板1.5 m 处，测孔垂直于巷道帮壁，水平向下倾斜5°，钻孔深度设计为3.5 m，钻孔直径为50 mm。从图11可以看出：随着扰动次数增加，造成围岩损伤增加，且损伤增量也增加，该趋势与模拟结果一致。此外，爆破产生的强冲击在较少扰动次数就导致围岩产生10%左右损伤增量。当扰动强度较小，但扰动次数足够多，同样也会造成较严重的围岩损伤破坏。对比图10和图11可以看出：模拟和实测的损伤增量变化趋势是一致的，但由于测点3位置岩性不同和测量误差的存在，其损伤增量与测点1和测点2的差别较大。

图10 不同扰动次数的测点损伤增量曲线Fig.10 Damage increment of observation points under different times of disturbance

图11 现场实测不同爆破扰动次数下损伤增量曲线[37]Fig.11 Damage increment of field monitor points under different times of blasting[37]

4.3 埋深对围岩破坏的影响

煤层埋深决定了地应力水平，埋深越大，地应力越高。通过设置不同煤层埋深，得到了不同埋深条件下围岩破坏规律。图12所示为不同埋深条件下巷道围岩遭受100次扰动后损伤分布。从图12可以看出：埋深越大，围岩损伤程度和范围越大。在埋深为400 m时，在顶底板围岩内损伤范围仅位于顶底板。随着埋深增加，最大损伤程度增加，而且损伤范围也增大。在埋深为800 m时，围岩内出现多条贯通的损伤带，并且逐渐向深部围岩内扩展，形成损伤破坏带。受动力扰动影响，左侧围岩内损伤发育要明显比右侧的高。当埋深达到1 000 m时，左侧围岩损伤程度严重，左帮底脚已出现严重破坏。损伤破坏带延伸至深部，在水平方向上围岩损伤破坏范围约是4 m，垂直方向上达8 m。对比不同深度围岩损伤程度和范围可以发现：在深部埋深时外部扰动造成围岩的最大损伤程度更大，而且损伤范围更广。这说明了埋深的增加导致围岩整体应力水平更高，更易产生破坏进入塑性损伤状态，且损伤带更易贯通，造成围岩的整体失稳破坏。

图12 不同埋深围岩损伤增量示意图Fig.12 Damage increment of coal in different depth

5 结论

1)频繁动力扰动造成巷道左帮破坏严重，围岩产生较大位移，围岩损伤破坏导致形成多条贯通的损伤破坏区。在地应力和频繁扰动应力共同作用下，左帮围岩受动力扰动破坏影响，塑性区内裂隙大量扩展和发育，引起煤体的损伤累积，在顶底板围岩裂隙贯通，形成多条连通的损伤带。最主要的损伤贯通带距离左帮约2 m，由底板延伸至巷道左侧上部，与顶板损伤带交汇于巷道左上方。

2)动力扰动次数决定了围岩损伤的累积量，造成围岩破坏形态的不同。随着扰动次数的增加，左侧围岩损伤程度明显增加，损伤范围也增加。左侧底部的损伤区域向内部延伸。损伤区域更加集中，而且损伤程度明显大于其他区域的损伤程度。扰动次数超过临界点后，围岩损伤程度大幅增加，易引起围岩区域性的严重破坏。

3)不同埋深下频繁动力扰动造成围岩破坏特征不同。在埋深较小时，围岩变形和破坏较轻，损伤破坏不明显。随着埋深增加，围岩地应力增加，在扰动应力的叠加作用下，导致围岩最大损伤程度增加，而且损伤范围也增大加剧，损伤带延伸距离更远。埋深的增加导致围岩整体应力水平更高，更易产生破坏进入塑性损伤状态，且损伤带贯通范围增大，更易造成围岩的整体失稳破坏。