基于阶跃响应的设备建模实验方法研究

鲁 博， 张寿明

(昆明理工大学电子信息与自动化学院，云南 昆明 650500)

1974年，P.E.ykhoff定义：“辨识问题可以归结为用一个模型来表示客观系统(或者将要构造的系统)本质的一种演算，并用这个模型把对客观系统的理解表示成有用的形式”，辨识要有三个要素—数据、模型、准则，辨识就是按照一种准则在一组模型类中选择一个与数据模型拟合最好的模型，辨识方法有阶跃响应法、脉冲响应法、频率响应法、最小二乘法、极大似然法，神经网路辨识等，本文对由模拟电子元器件组成的基本一阶系统，输入端给阶跃输入，应用示波器采集输入、输出信号，应用实验数据及阶跃响应法的两点法、MATLAB辨识工具辨识，及最小二乘法辨识对象，然后和计算结果进行比较，能给出较好的辨识参数。

伐木与木质加工设备要想实现生产的产品品质高，绿色化、能源节约化，就必须对设备进行建模，才能更加稳、准、快地进行生产调控，王艳伟等在木材干燥技术研究中提出干燥设备需要通过建模才能达到绿色节能控制，汪海涛等研究了免疫控制器在木材干燥系统中的应用，提高了板材品质，宋洋等研究一阶系统，利用改变电枢电压的方法完全可以实现对电机堵转转矩的控制，从而实现对机械臂的位置控制。

通过模拟器件构建一阶电路，应用模拟电路来代替实际系统，然后测量其阶跃响应曲线，根据曲线识别系统参数，同时采集输入/输出数据，应用两点法、最小二乘法、辨识工具箱、神经网络法实现系统建模。

1 方法及原理

一阶系统模拟电路原理图如图1所示(用multisim仿真完成，可得到系统输出)，主要器件由ua740y运算放大器组成，是由积分反馈环节组成的反向一阶环节和反相器组成，理论结果为一阶系统。

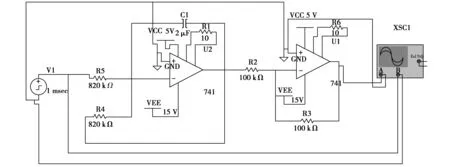
图1 一阶系统模拟电路原理图

对于运算放大器基本理论i0=i1-i2，得：

(1)

(2)

画出方框图，其中T=RoC，后面再级联一个反相器，所以有：

(3)

令ui(t)=1(t)，即Ui(s)=1/S，则系统的输出为：

(4)

取拉式反变换，可得：

(5)

带入数据T=RoC=820×103Ω×2×10-3F=1.64。

所以对象函数为：

2 两点法辨识法

所谓两点法，就是利用阶跃响应yt上两个点的数据去计算T和τ，由机理分析知此模拟电路是最常见的一阶系统，因为器件的滞后性，设对象的传递函数为：

(6)

式中：K为系统增益；T为时间常数；τ为迟延时间。在t=0时，施加阶跃信号：

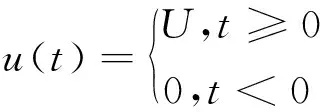
(7)

在系统输入端、系统输出端收集信号，迟延时间τ可以从输出响应曲线上直接读出，从而一阶迟延系统的阶跃响应为：

(8)

通过拉氏变换得：

y(t)=KU(1-e-(t-τ)T)，t≥τ

(9)

系统稳态值为y(∞)=KU，从而可以得到：

(10)

当t→∞时，将阶跃响应归一化，选取两个观测点数[t1，y(t1)]、[t2，y(t2)]，据此得到关于T和τ的方程：

y(t1)=1-e-(t1-τ)/T

(11)

y(t2)=1-e-(t2-τ)/T

(12)

求解方程组得到一阶迟延系统传递函数参数估计为：

(13)

(14)

选定特定观测数据，如y(t1)=1-e-1/2=0.393 47，y(t2)=1-e-1=0.632 12，此时有：

(15)

(16)

从阶跃响应曲线中读出时刻t1和t2(稳定值的39.347%、63.212%对应的时刻)，从而得到T和τ的估计值为：

(17)

(18)

3 最小二乘法辨识法

最小二乘法(least square，LS)在1795年由高斯提出，后来成为估计理论的基石，最小二乘法原理简单、收敛较快、易于编程，所以在系统参数估计中得到广泛应用，这种方法是运用最小二乘的原理，目标函数为广义误差的平方和，通过使目标函数最小来确定模型的参数。

结论为有L组输入输出观测数据{y(k)，u(k)，k=1，2，…，L}，利用批处理方法得到系统参数的最小估计值为：

(19)

式中：

4 BP神经网络辨识法

神经网络不仅具有很快的自学习速度和局部逼近的能力，它还具有原理简单、容易在工程上应用的优势。在神经网络通过学习辨识对象输入输出数据的基础上，且误差函数也能满足要求的前提下，可得到一个能够描述对象输入输出关系的系统模型。

4.1 BP神经网络结构及辨识算法

该研究应用SISO三层BP神经网络结构如图2所示，BP神经网络辨识结构如图3所示。

图2 BP神经网络结构

图3 BP神经网络辨识结构

(20)

(21)

输出层神经元输出为：

(23)

网络输出与期望输出的误差为：

e(k)=y(k)-ym(k)

(24)

式中：y(k)、ym(k)分别为网络输出和期望输出。

取性能指标函数为：

(25)

隐含层输出权值为：

(26)

此式考虑积累经验，其中a为动量因子。

(27)

输入层至隐含层权值为：

(28)

此式考虑积累经验，其中a为动量因子。

(29)

4.2 辨识步骤

(1)输入系统初始数据，设置BP网络初始权值；

(2)采样期望输出y(k)，并用式(20)～(23)计算当前网络输出ym(k)；

(3)应用式(27)和式(29)计算权值增量；

(4)应用式(26)和式(28)计算权值；

(5)返回第二步，继续循环。

5 实验过程

5.1 实物连接测试过程

连接电路如图4所示，首先将阶跃信号连接示波器调输出为1 V大小，然后调节运放的调零端，再将输入加在一阶电路的输入端，用示波器测量输入、输出。

图4 实物连线图

通过示波器测量，显示如图5所示，同时可通过选择usb得到相应csv格式数据。

图5 示波器慢滚动显示图

5.2 两点法辨识过程

5.3 MATLAB辨识工具辨识

应用MATLAB的ident辨识工具，拟合对象及辨识参数，步骤如下：

在MATLAB命令窗口输入ident或者在MATLAB左下角选择对应的stat中选择toolboxes，到选择identification 中的ident GUI，然后在窗口中选择采集的数据分别为输入和输出数据，models选择带滞后环节，最终得到图6图像和辨识拟合度为99.27%，及图7所示传递函数。

图6 辨识图像及拟合度

图7 辨识工具辨识所得传递函数

其中K为10 146，将输入1 V换算成MV，对应输入K为1.046，Tp=1.961，Td=1.0672，其传递函数为：

结果与两点法辨识结果基本相同。

5.4 最小二乘法模块辨识

通过x=lsqnonlin(fun，x0)从矩阵x0中找到一个x矩阵使函数的平方和最小，同时编写M函数迭代调用，同样可以得到相应函数，如图8所示。

图8 最小二乘法辨识所得传递函数

其中K为10 145，将输入1 V换算成MV，对应输入K为1.045，Tp=1.961，Td=1，其传递函数为：

5.5 BP神经网络辨识

应用BP神经网络辨识效果和全局误差如图9所示。

图9 BP神经网络辨识效果和全局误差

可以看出应用BP神经网络辨识效果非常好，神经网络输出值紧紧跟随实际输出值，并且只需要训练35步就可以达到误差基本为零。

6 结论

通过三种辨识方法的输出图像可以发现不管哪种辨识方法，其T大小都基本接近理论方法，同时也可以发现系统有一定的滞后性，辨识结果都有τ存在，这个也符合过程控制中对象存在时滞性的问题；但是两点法相比用辨识工具法和二乘法(批处理)得到的τ参数相差较大，从两点法的τ推理过程可以发现，τ与起始点没有关系，所得参数τ较小，而辨识工具辨识和最小二乘法得到的τ参数较大，比较合理，同时应用BP神经网路辨识效果较好，简洁、快速。