基于氧化铝陶瓷磨削实验的超薄金刚石砂轮三维建模研究

庄朋,张幼军,冯双,胡涛

（沈阳工业大学机械工程学院,辽宁沈阳 110870）

现阶段精加工领域对磨削加工后的表面质量要求越来越高,如与现在科技发展密切相关的半导体行业,硬脆材料中的玻璃、陶瓷和单晶硅等材料使用磨削加工为最后的材料加工成型步骤,将加工后的表面粗糙度,单位面积内的崩边数量等损伤参数作为评价参数[1].氧化铝陶瓷是典型的硬脆材料[2],因其具有高强度、高耐磨性、良好的化学稳定性等优异性能,在机械、电子、国防和航空航天等领域应用广泛[3],而且氧化铝陶瓷是目前世界上使用范围最广、产量巨大,应用范围最广的陶瓷之一.氧化铝陶瓷主要成分以α-Al2O3粉体为主,并且其备料简单,原料充足，对于钢铁而言其重量轻、密度较小[4-8].

在国内熊万里等学者对氧化铝陶瓷进行了高速磨削实验,其实验结果说明在提高砂轮线速度的同时,加工过程中的磨削力更为平稳,相较于以往传统工艺的表面质量比较,磨削完的表面质量较高[9].黄含在进行同样的磨削实验时使用了树脂金刚石划片,对氧化铝陶瓷进行了高速精密切割实验，揭示了氧化铝陶瓷等硬脆材料的磨削机理,在此基础上还研究了高效率磨削氧化铝陶瓷的力学公式[10-12].谢桂芝等学者对氧化铝陶瓷加工进行了工艺参数的分析,对包括表面质量,磨削温度等性能进行了表征[13].对磨削氧化铝陶瓷的刀具进行研究发现,磨粒等脱落程度对金刚石砂轮的使用寿命影响更大[14].李曙生对金刚石磨粒的排布问题进行了研究,从金刚石刀具角度研究了磨削机理[15].

氧化铝陶瓷作为一种重要的超硬材料，其应用极为广泛,在结构陶瓷、电子陶瓷、光学陶瓷中都有着举足轻重的地位[16].氧化铝陶瓷由于性能优良、密度小质量轻、加工精度高等特性且具备形成薄膜涂层优势,在半导体基板、封装材料、介电元件和绝缘膜等方面被广泛应用[17].由于其自身特性导致传统加工工艺方法难以满足现阶段的精度要求,所以氧化铝陶瓷加工需要一种新的方法.

超薄金刚石砂轮切割片作为新兴的磨削工具,其磨削过程主要通过磨粒的二面角在工件的表面进行划擦去除材料,利用其去除材料少的特点,得到符合加工要求的表面质量.

本文研究超薄金刚石切割片表面的三维建模,通过ABAQUS 软件对氧化铝陶瓷进行磨削仿真[4],最后进行磨削实验验证三维模型的准确性.

1 超薄金刚石砂轮切割片表面的三维建模

1.1 砂轮表面的微观形貌

使用扫描电镜对超薄金刚石砂轮切割片进行微观形貌观察,图1 为200 μm 单位下微观形貌,砂轮表面的磨粒是随机分布的,其刃露出量也各不相同,在建立模型时需要考虑磨粒在表面排布的随机性[18],可以看出在200 μm 单位面积内,同一行参与磨削的磨粒数多为3～4 颗,图2 为50 μm 单位下微观形貌,可以明显看出金刚石磨粒,且形状为不规则的多面体.说明经过后期研磨,去除毛刺,切割片外圆修整效果优异,金刚石磨粒明显露出,随机分布在结合剂之上,形貌较为完整.

图1 砂轮200 μm 微观形貌Fig.1 Micromorphology of grinding wheel at 200 μm

图2 砂轮50 μm 微观形貌Fig.2 Micromorphology of grinding wheel at 50 μm

1.2 磨粒几何参数的确定

结合磨粒形状表面形貌观测,由于磨粒形状具有一定的不规则性,提高了模拟的难度.本文简化金刚石磨粒为多面体形状,实验采用的超薄金刚石砂轮切割片中磨粒目数为400 N,换算得出其单颗磨粒直径大约为37 μm 左右,使用Python 语言对ABAQUS 软件进行二次开发,首先建立一定范围直径的磨粒,规定磨粒最大与最小直径使用[Dmax,Dmin]代替,利用Python 语言中的random.uniform 函数生成[Dmax,Dmin]内的随机数,保证其磨粒粒径在合理范围,利用圆外切线生成不同菱形缺口的切割件,对正方体进行不同方向、不同次数的随机切割,进而生成不同形状的磨粒,其流程大体如下:

(1)在全局坐标系原点建立直径在[Dmax,Dmin]范围内的圆.

(2)利用Python 语言中的random.randin 函数选取输入直径圆上[45°,89]任一角度,设角度为θ,使用X=sin(θ),Y=cos(θ)确定圆上的一点,通过切线方程求出交于Y 轴的点,利用这两点确定一条直线,同理选取[91-149]圆上的一点,确定切线方程,利用几何关系求出两条切线的交点,利用此原理,接着选出4 个交点.

(3)在ABAQUS 后台程序中使用s.Line(point1=(x,y),point2=(x,y))命令给串联取出的四个交点形成菱形.

(4)利用ABAQUS 内核rectangle 语句生成矩形,拉伸形成切割件.

(5)建立Dmax 为边长的正方体.

(6)将切割件与被切割件拉进装配模块,进行中心移动Dmax/2 的距离,使两个部件中心在坐标原点处,使用PYTHON 中的random 函数,让切割件分别绕X,Y,Z 轴进行随机角度的旋转,确定切割位置.

(7)切割后的磨粒如图3 所示.

图3 不同切割次数、不同形状的磨粒Fig.3 Abrasive particles with different cutting times and shapes

1.3 砂轮几何参数的确定

在二次发开的程序中使用For 循环函数中的for i in range(N),N 代表磨粒数目,跟据实际情况输入相应的磨粒数进行备用.使用s1.Circle By Center Perimeter(center=(x,y),point1=(x,y))中心为原点,点1 中的X 坐标为砂轮半径,依据命令建立砂轮基体,将两者放进装配模块,确定磨粒位置前使用PYTHON 中的|[0|360°]函数确定随机角度,使磨粒分别绕自身的X,Y,Z 轴进行随机角度的旋转,模拟磨粒与结合剂反应时自身位置.为简化模拟磨粒在砂轮表面位置的随机性,避免磨粒相互重叠,采用前文中在圆上取点命令(X=sin(θ),Y=cos(θ))进行类似斜齿轮的磨粒排布,接着采用固定磨粒中心在砂轮外表圆的方法,即在砂轮外表面选取的圆上均匀布点[19],并随机选取磨粒放置在相应的点上,实现砂轮的三维建模,如图4 所示.由于仿真实验条件限制,简化建立宽度为100 μm,截取外径为58 mm 模型中的1°为磨削工具,结果如图5 所示.

图4 整体砂轮建模Fig.4 Modeling of integral grinding wheel

图5 外径(58 mm)的1°砂轮Fig.5 1° grinding wheel with outer diameter (58 mm)

2 切割氧化铝陶瓷仿真实验与设置条件

研究所采用试验材料为氧化铝陶瓷材料,模拟切削试验条件如表1 所示.砂轮整体设置为刚体,氧化铝陶瓷在磨削时呈现脆性断裂,因此,在目前的有限元分析中采用ABAQUS 显式脆性开裂本构模型,当材料中的最大主应力超过其抗拉强度时,材料发生分离[20-21].如图6 所示,实验部分采用DS610 精密划片切割机,此机型主要用于硅集成电路,纤维复合材料,氧化铝等类型的陶瓷,蓝宝石等硬脆性材料的精密切割,其技术性能如下,控制系统由工业计算机和轴卡安装组成,由于转台为圆形,其最大加工尺寸为6英寸.转台经过磨床加工,平整度在±0.006 mm,X 轴采用伺服电机驱动,调速范围为0.1～500 mm/s,Y 轴采用直线导轨,滚珠丝杠和光栅反馈闭环控制,全程定位精度<0.004 mm/160 mm.Z 轴采用直线导轨和滚珠丝杠传动方式,重复定位精度0.003 mm.θ 轴采用伺服电机驱动,精密360°转角机构,其分辨率可以达到0.000 5°.高清的CCD 与高倍显微镜组成图像系统,状态实时显示,操作方便.如表2 所示,实验采用SDC400N25M超薄金刚石砂轮切割片用作切削工具,结合剂为铜锡组合,采用热压方式进行压制,然后经过修磨成型.工件单片规格为5*40*40 mm 尺寸的氧化铝陶瓷.

图6 实验工作台Fig.6 Experimental bench

表1 氧化铝陶瓷仿真参数Tab.1 Simulation parameters of alumina ceramics

3 氧化铝陶瓷切割仿真与实验结果分析

3.1 主轴转速对氧化铝陶瓷切割力的影响

图7 为不同主轴转速切割氧化铝陶瓷的实验与仿真磨削力点线图,由图可知,五种不同转速下磨削力整体趋于下降,随着主轴转速增加,磨削所需要的磨削力越来越小,主轴转速由20 000 r/min 增加到30 000 r/min 时,磨削力下降幅度变小,但在25 000 r/min 主轴转速后磨削力稍微上升,结合图8 磨削力起伏程度,分析原因主轴转速的提高及主轴振动增加及切割片离心力的作用造成砂轮本身的弹性变形,最终导致磨削力的增加,仿真由于边界条件的设定导致整体磨削力比实验中的磨削力高,因为忽略振动与温度影响导致在30 000 r/min 时实验的磨削力高于仿真的磨削力.

图7 不同转速下实验与仿真磨削力对比Fig.7 Comparison of experimental and simulated grinding forces at different speeds

图8 不同转速下磨削力波动过程Fig.8 Grinding force fluctuation process at different speeds

3.2 主轴转速对氧化铝陶瓷切割表面质量的影响

图9 为氧化铝陶瓷在主轴转速20 000 r/min,进给量4 mm/s,切深0.2 mm 的磨削条件下的材料断裂情况.很明显,随着磨粒施加力逐渐增强,磨粒楔入能有效地去除断裂的材料,并且将断裂的材料沿切线方向推出，不会造成磨削区域发生明显的弯曲,但对邻近的材料影响范围较大.由于砂轮表面磨粒的刃露出量不同,造成硬脆材料的崩边,显示切口不平整,磨削完的表面高度不同,与图10 同等实验条件的现实结果相似,验证了三维模型的准确性.

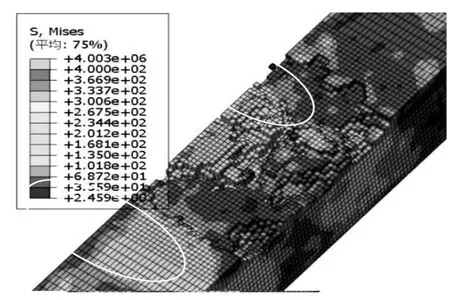
图9 仿真结果Fig.9 Simulation results

图10 实验结果Fig.10 Experimental results

如图11 所示,随着主轴转速的增加,材料边缘大于25 μm 背崩边数逐渐下降,当转速达到25 000 r/min时,背崩边数达到最少,但之后继续增加主轴转速,崩边数反而增加.分析原因是转速增加,切割片与工件之间磨削热的积累降低切割片锋利程度.说明在主轴转速为25 000 r/min 时氧化铝陶瓷表面质量最好,对应图8 主轴转速下切割力较为稳定.

图11 大于25 μm 背崩边数Fig.11 >25 μm back edge collapse number

3.3 进给速度对氧化铝陶瓷切割力与表面质量的影响

如图12 所示,固定主轴转速为24 000 r/min,切割深度0.2 mm.随着进给速度的增加,磨削力大小从0.24 N 左右上升到0.5 N 左右,但当进给速度达到6 mm/s 时,磨削力下降为0.3 N 左右.并且可以看到进给速度为4 mm/s 时,磨削力波动程度更大,结合图13 其崩边数量也是最多,表面质量最差.分析原因除却材料本身的不均匀因素,可以得出金属金刚石切割片在4 mm/s 进给速度下进行磨削时,刀具与工件之间的磨削热积累更快,磨粒脱落程度更高,造成整体磨削力变大,并且波动程度最大.

图12 不同进给速度磨削力变化Fig.12 Grinding force changes at different feed rates

图13 边缘大于25μm 背崩边数Fig.13 Back edge collapse greater than 25 μm

3 结论

通过圆外切线的方法建立多面体磨粒,使用扫描电镜观察切割片表面形貌,利用PYTHON 语言中的随机函数确定磨粒最终角度,采用均匀布点的方式确定磨粒的排布,可以建立较为准确的三维模型.

进行氧化铝陶瓷的仿真实验,磨削力随着主轴转速的增加而减小,由于边界条件影响,相同条件下的仿真结果大于实验结果,但与同等实验条件的现实结果相似,验证了仿真模型的准确性.

结合仿真,主轴转速在25 000 r/min 时磨削力最小,波动也最平稳,观察实验后的崩边情况,证明此转速下切割氧化铝陶瓷效果最好,与其他工艺相比,利用超薄金刚石砂轮切割片加工氧化铝陶瓷更加容易满足精度要求.