基于改进PSO的压铸自动化生产线优化调度

陶丽华，迟晓晨，谷东伟

（长春工业大学 机电工程学院，长春 130012）

0 引言

随着信息技术和人工智能的发展，智能制造作为“中国制造2025”国家战略的重要举措，已经引起各个行业的广泛关注[1]。铸造行业作为制造业的重要基础产业，迫切需要进行智能化转型升级，压铸自动化生产线（Die casting automatic production line，简称DAPL）已成为现代压铸企业提高生产效率、消除重体力劳动和清洁环境的重要举措。多品种小批量DAPL智能调度属于一类带有运输机约束的并行机调度问题（Parallel Machine Scheduling Problem，PMSP），运输机作为原料供应站与压铸机之间的纽带，确定合适的运输机速度，优化原料到各压铸机的调度序列，实现原料在各压铸机之间无障碍流转，减少压铸机的空闲等待时间，对于压铸企业实现清洁生产、提高生产效率、降低成本具有重要的现实意义。

1 基于多目标的DAPL调度数学模型建立

1.1 问题描述

某铝制品DAPL由一台运输机和多台不同类型的压铸机组成，运输机为各压铸机服务，每次运送一个坩埚的高温铝液到某一压铸机进行压铸生产。DAPL调度问题是一类带有运输机约束的异构并行机调度问题，可描述为：1）有多台机器，每台机器生产与自身模具对应的一种类型的铝件，产出的铝件可自动进入后续产线。2）每个坩埚的铝液只在一台机器上压铸生产，产出一定数目的某类铸件。所有坩埚的铝液容量是相同的，每个坩埚的铝液可被运往机器集中的任一台机器上生产。3）同一时刻一台压铸机只能对单位坩埚铝液进行操作加工。4）每个坩埚的铝液在机器的生产过程中是不可中断的。5）假定运输机是匀速的，运输机每次从供应站运送一个坩埚的铝液到机器，然后，运输机返回供应站继续运输，运输机在供应站和机器之间的运输过程是不可中断的。

1.2 符号定义

为了准确描述DAPL调度问题的数学模型，定义符号如下：hT为每日工作时间；M为机器集合；m为机器数量；N为hT内完成的坩埚铝液集合，坩埚数量nc；n为铝件的类型数，n等于m；OMj为单位坩埚铝液在机器j上的产出铝件数；nj为j机器计划产出铝件数量，假定数值是OMj的整数倍；v为运输机速度；vmin为运输机速度最小值；vmax为运输机速度最大值；DSj为供应站与j机器的距离；yTj为运输机在供应站和j机器之间的运输时间；mTi，j为i坩埚铝液在机器j上的压铸时间；BTi，j为i坩埚铝液在机器j的开始时间，i=1，2，...，nc，j=1，2，...，m；ETi,j为i坩埚铝液在机器j的完成时间，i=1，2，...，nc，j=1，2，...，m；aBTi,j为运输机运送i坩埚铝液从供应站到机器j的出发时间，i=1，2，...，nc，j=1，2，...，m）；aETi,j为运输机运送i坩埚铝液从供应站到达机器j后，返回供应站的时间；Mi为i坩埚铝液的加工机器；Cj为机器j上最后一个坩埚的完工时间；xi,j=1时，i坩埚在机器j上生产；xi,j=0时，i坩埚不在机器j上生产。

1.3 DAPL多目标调度数学模型

在DAPL中运输机速度的改变直接影响运输机运送铝液到达机器的时间，从而影响坩埚铝液的生产调度。为了提高DAPL的效率，需要确定合理的运输机速度和坩埚铝液的机器调度序列，避免因运输机速度过快而造成铝液溢出，并避免因速度过慢而增加机器的空闲等待时间，在规定的时间段和机器计划产量的约束下，以机器总空闲时间最短、设备负荷均衡、最大化产出铝件数和最小化运输机等待时间为目标，并采用加权平均法建立DAPL优化调度的多目标数学模型。

1）以所有压铸机的总空闲时间最少作为优化目标f1如式（1）：

其中：式（2）表示每台机器的结束时间，式（3）指运输机匀速运行，式（4）指第1个坩埚铝液进入系统的时刻0，式（5）指运输机在供应站和机器之间运输过程不可中断，式（6）指每坩埚铝液一旦开始生产就不能中断，式（7）指每台机器同一时刻只能加工一个坩埚铝液，式（8）和式（9）指速度和时间限制。

2）设备负荷的均衡程度定义为优化目标f2，如式（10）所示，设备负荷的均衡程度用各机器负荷的方差表示，各机器负荷的均值如式（11）所示：

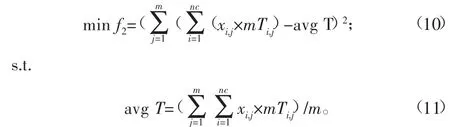
3）以所有机器产出的铝件数为优化目标f3，由于f1和f2这两个目标的优化是求解最小化问题，为了使f3目标的优化与f1和f2保持一致，将f3目标的最大化问题转化为最小化问题，如式（12）所示。其中，B为忽略运输机的所有机器在hT时间段产出铝件的数量，如式（13）所示，式（14）指每台机器产出铝件的数量受制于计划产量要求：

4）在运输过程中，为了使铝液在坩埚中保持尽量平稳，运输机的速度越小越好，运输机速度越小，运输机总等待时间越短，定义运输机的总等待时间为优化目标f4，如式（15）所示：

2 改进粒子群算法设计

2.1 改进粒子群算法流程

为了提高压铸自动化生产效率，减少设备的空闲等待时间，实现一个流的均衡生产和清洁生产，依据1.3节数学模型，在标准粒子群算法（Particle Swarm Optimization，简称PSO）的基础上提出一种改进的粒子群算法求解DAPL中运输机速度及调度优化问题。在粒子进化过程中，速度的更新依赖个体极值和群体极值，容易造成算法的提前收敛，因此将一定数量的较好的个体极值和群体极值保存起来，分别建立个体极值库和群体极值库。针对每一个当前粒子，分别将个体极值库中的每一个个体极值和群体极值库中的每一个群体极值配对，利用每一对个体极值和群体极值对当前粒子进行速度和位置的更新，可得到多个临时粒子，并采用模拟退火算法（Simulated Annealing，简称SA）对每个临时粒子进行局部寻优，根据优化后的临时粒子更新个体极值库，并将最优临时粒子作为当前粒子的新一代粒子。以每一代粒子群的个体极值库更新群体极值库。个体极值库、群体极值库的建立与基于SA的优化改进提高了PSO的搜索效率和寻优能力。改进粒子群算法流程如图1所示。

图1 改进粒子群算法流程

2.2 改进粒子群算法的操作设计

1）粒子的编码和初始粒子群的生成。每一个粒子的位置采取一维实数进行编码操作，实数值即为运输机的运输速度。给定粒子位置和速度的搜索范围，为了保证初始粒子群的多样性，在该范围内随机生成初始位置与初始速度[2]。

2）适应度函数的设计。以综合目标值的大小评价粒子的优劣[3]，适应度函数G(v)定义见式（20）：

3）粒子的更新。粒子的更新分为粒子的速度更新和位置更新[4]，速度更新如式（21）所示，位置更新如式（22）所示。在速度更新中，通过扰动因子δ干预个体极值和群体极值，避免算法提前收敛，提高算法的开发能力，并引入动态惯性权重w均衡算法的搜索能力，w的取值与进化代数gen有关，如式（23）所示。动态惯性权重w使算法在进化的早期以较大惯性继承粒子当前的速度，搜索力度较大，从而实现全局搜索；在后期算法以较小惯性继承粒子当前速度，使算法尽快收敛于全局最好解[5]。

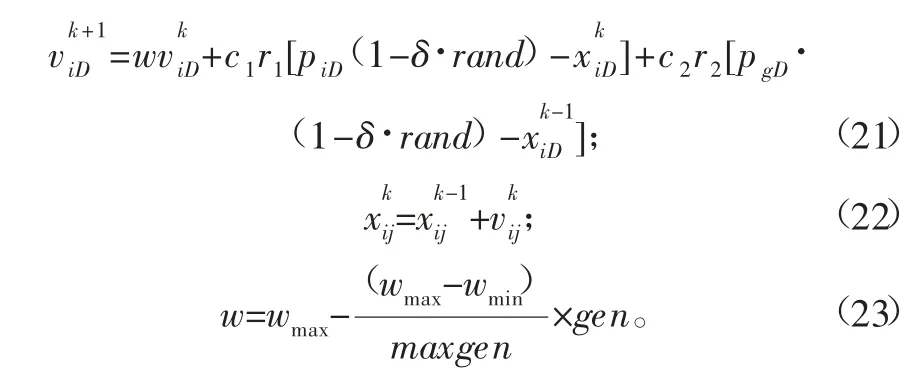
式中：wmin∈(0,1]；c1和c2为学习因子；piD为i粒子的个体极值；pgD为群体极值；gen为当前代数；maxgen为最大代数。

4）基于SA算法的局部寻优[6]。在粒子的更新过程中，将当前粒子作为初始解，采用SA算法对当前粒子进行小范围细致搜索，以提高算法的局部寻优能力。

5）保优策略。在每一代粒子更新后，通过个体极值库的更新记录粒子到目前为止遍历过的10个最好位置，并根据所有个体极值库的最优粒子中的前4个粒子更新群体极值库，使得全局最优粒子始终保留在群体极值库当中，避免了最优粒子在算法进化过程中丢失。

6）停止准则。当算法运行至最大代数时终止，输出最优粒子对应的运输机速度和该速度下运输机运送坩埚的最优调度序列。

3 实验仿真

3.1 实例验证

某铝制品压铸自动化生产线由5台压铸机、1台运输机和1个供应站组成，运输机负责将高温铝液运送到各压铸机，设备信息如表1所示。采用本文提出的改进粒子群算法确定运输机的最佳速度和每日各坩埚铝液的调度分配序列。

表1 设备信息

假定每日工作时间为8 h（即480 min），各优化目标权重及比例系数如表2所示，粒子群规模为50，学习因子c1和c2均为1.494 45。惯性权重w取值范围为[0.4,0.9][7]，扰动因子为0.01，运输机速度范围为[10，30] m/min，个体极值库的规模为10，群体极值库的规模为4，算法运行100代。SA的初始温度为100 ℃，停止温度为20 ℃，降温速率为0.9，等温链长为30。各目标的收敛曲线如图2所示，其中星号代表最优解，括号中左侧数据为目标最优时的代数，右侧数据为目标值。

表2 目标的权重及比例系数

由图2可见，随着代数的增加，算法运行到第4代时总目标收敛于最小值717.5194，此时运输机最佳速度收敛于21.9968 m/min，机器总空闲时间收敛于38.197 min，各机器负荷的方差在第1代就收敛于24，各机器产出铝件数在第1代就收敛于622个，运输机等待时间在第4代收敛于274.53 min。坩埚铝液在各机器上的最优分配序列如表3所示，表3显示当日58个坩埚铝液的设备分配情况，基于设备的调度甘特图如图3所示。

图2 各目标收敛曲线

图3 基于设备的调度甘特图

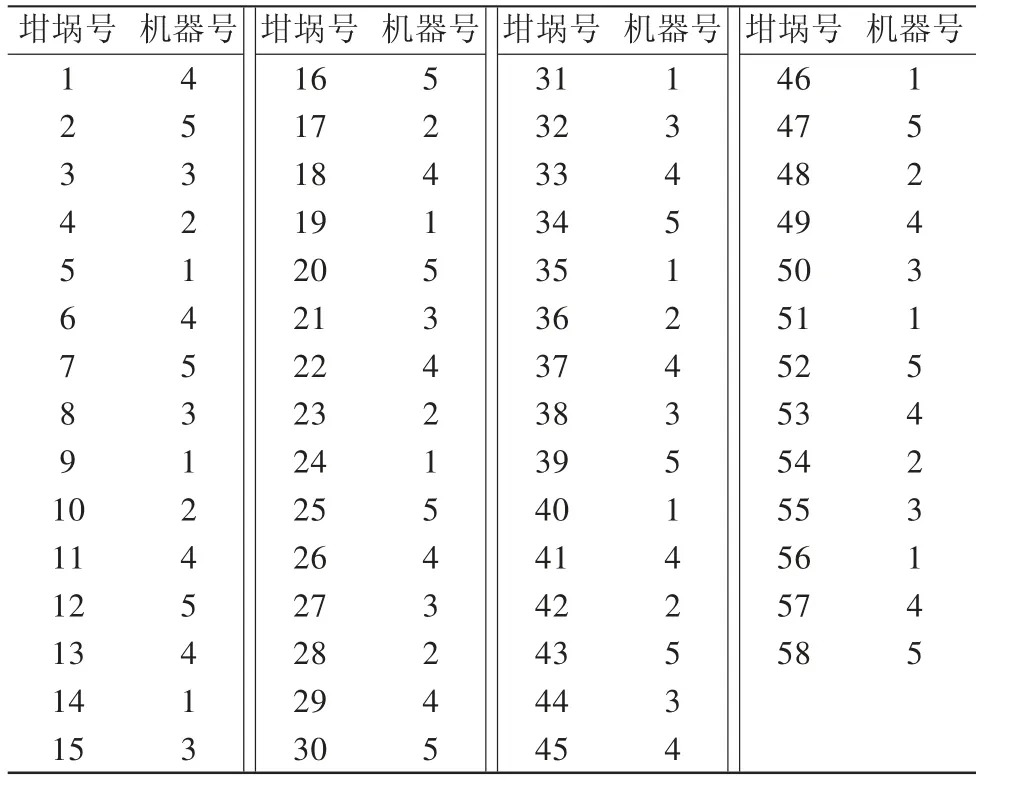
表3 坩埚-设备的调度分配

由图3可见，运输机和压铸机的调度采用不同的颜色表示，在压铸机上每个矩形框代表某坩埚铝液在机器上的停留时间，上边的数字代表坩埚铝液的序列号，例如压铸机1生产坩埚铝液的顺序依次为5、9、14、19…。由图3可直观看出，在运输机速度达到21.9968 m/min时，各机器几乎满负荷工作，总空闲时间较少，仅为38.197 min，各机器负荷比较均衡，在8 h内各机器共完成58个坩埚铝液的生产，共产出铝件数622件。运输机作为瓶颈设备需要不停地在各机器间流转，运输机上每个矩形框代表运输机为了运送某坩埚铝液到机器，从供应站到机器再返回到供应站的时间，虽然运输机比较繁忙，但当运输机达到最佳速度21.9968 m/min时，运输机的总空闲时间最短为274.53 min。因此，采用本文提出的改进粒子群算法较好地解决了某压铸自动化生产线运输机最佳速度的求解问题，降低了各压铸机的总空闲时间，实现了压铸自动化生产线一个流的均衡生产。

3.2 算法的性能验证

Rosenbrock函数又称为香蕉函数，是用来评价算法搜索性能的著名测试函数[8]，函数式如式（24）。该函数的特点是在[100,100]n上只有一个全局极值点，且在全局极小点临近的狭长区域内取值变化极为缓慢[9]，如图4所示，常用该函数评价粒子群优化算法的搜索性能：

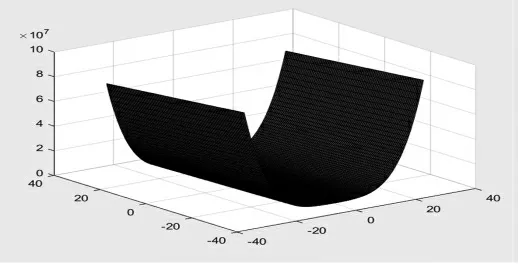
图4 Rosenbrock函数图

为了测试本文提出的改进粒子群算法的寻优性能，利用本文提出的改进粒子群算法分别求解维度为30、100、500、1000的Rosenbrock函数的极值点，粒子群规模为30，算法进化500代，SA的初始温度为100 ℃，停止温度为20 ℃，降温速率为0.9，等温次数为30，运行100次。运行结果与文献[10]之间的对比如表4所示，文献[10]采用花授粉算法求解各维度下的Rosenbrock函数问题。由表4可见，在求解不同维度的Rosenbrock问题时，本文提出的改进粒子群算法在100次运行结果的均值、最好解、最差解和标准差都远远优于文献[10]的算法。由此可见，本文提出的改进粒子群算法具有较强的寻优性能和稳定性。

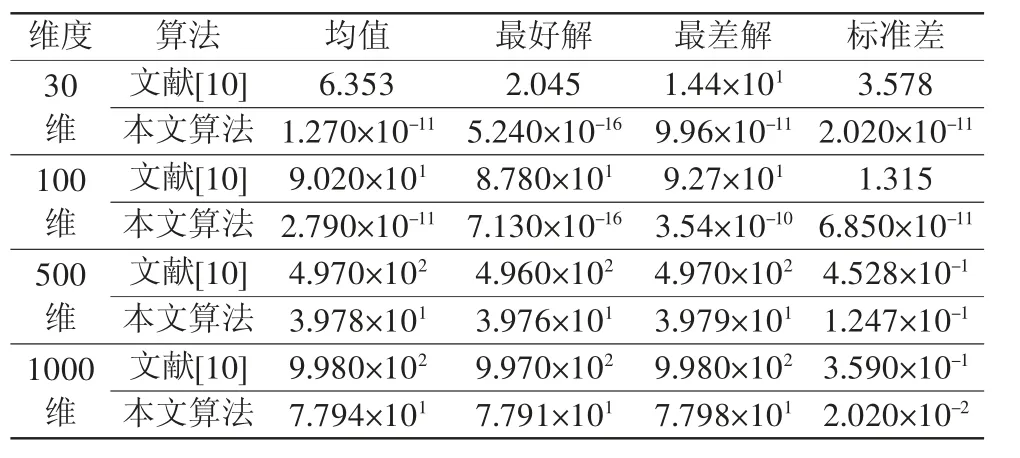
表4 两种算法数据对比

4 结论

压铸自动化生产线属于典型的异构并行机调度问题，其运输机最佳速度的确定直接影响生产线的效率和生产环境。本文以设备总空闲时间、设备负荷均衡、产出铝件数和运输机等待时间为目标，建立了DAPL多目标优化调度数学模型，提出了一种性能和寻优效率较好的改进粒子群算法对DAPL优化调度问题进行优化求解，满足了压铸自动化生产线一个流的均衡生产需求。在实际生产过程中，由于运输机的速度不一定是匀速的，若将运输过程中的加速和减速过程考虑进去，将更符合DAPL的生产实际。