等间距平行线辅助机器视觉实现工件尺寸测量

邱国清

（1.闽南师范大学 计算机学院，漳州363000；2.闽南师范大学 福建省粒计算及其应用重点实验室，漳州363000）

在机器视觉系统中，光源、相机选取的优劣是决定机器视觉成功与否的关键［1］，传统的成像系统都会有少量的畸变，图像会不同程度的拉伸变形，造成图像边缘轮廓失真，影响轮廓测量精度.栅格数据用一定的分解力把制图表像按行、列进行划分，从而得到离散的基本像元，与制图物体的空间分布特征有着严格而直观的对应关系，对物体的可探性强，为增强应用机器视觉效果提供了可能性.尺寸测量是机器视觉技术最普遍的应用领域，圆测量需要对圆的外形轮廓进行识别和拟合，在得到圆的方程之后即可根据数学方法获取相关的各种参数，如直径、圆心位置等.哈夫变换法是利用三维空间参数聚类提取圆的经典方法，图像空间中的圆对应着参数空间中的一个点，而图像空间中的一个点（x1，y1）对应着参数空间中的一个三维直立圆锥，该点约束了通过该点的一个圆锥面的参数（a1，a2，r）.最小二乘法的原理是先选择曲线的数学模型，再通过采样点的Y值与f（x）之差的平方和最小值来确定f（x）的系数［2］.但这两种算法计算量非常大，运算速度慢.而等间距平行线算法［3-5］通过绘制若干条平行线，计算每条平行线与轮廓交点坐标来测量工件的精度，计算量少，速度快.

1 等间距平行线算法

等间距平行线算法是在圆内绘制一组等间距平行弦，每条弦与工件轮廓交点可以利用勾股定理求出，利用这个原理对轮廓进行圆的拟合.该算法分两个主要内容：

（1）对一个工件轮廓区域进行轮廓跟踪，求出区域的边界像素点.

（2）根据像素点序列绘制一组等间距平行线，依次判断每条弦的两个端点是否满足勾股定理，如果满足则端点不用拟合，否则需要拟合.

1.1 绘制等间距平行线

（1）坐标Y轴与等间距平行线相互平行且多边形轮廓点均位于第一象限，设等间距平行线与原坐标系的y轴之间夹角为θ(-90°≤θ≤90°)，新坐标系下轮廓点的转换计算如下：

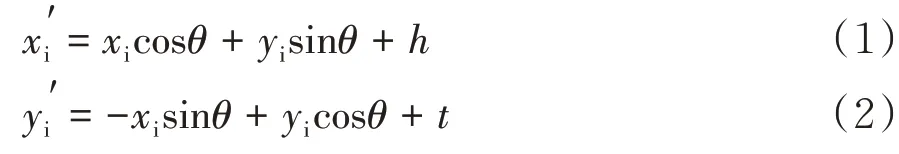
（2）为了能让每条平行线穿过区域内点，约定等间距平行线之间的间距等于栅格数据二维网格的大小，在工件轮廓边界像素点序列中求新坐标系中轮廓点横坐标的最小值和最大值，取轮廓点中横坐标最小值，d为等间距平行线的间距（等于网格大小），首先选定一条平行线开始推算，该平行线与新坐标系Y轴之间的距离称为a值，也就是第一条平行线的横坐标，即

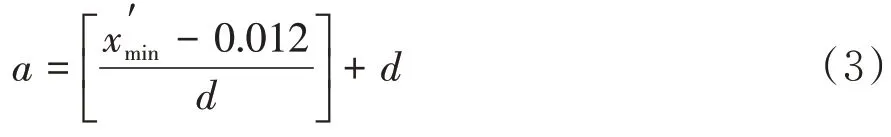
其中，［］为取整符号.

（3）成对读取边界像素点序列里的坐标值，绘制等间距平行弦，每条弦与轮廓两个端点计算如下：

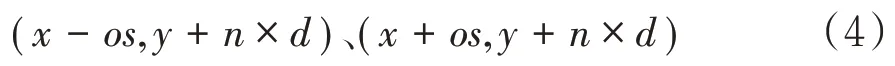
1.2 算法描述

（1）设置间距值，绘制平行线，扫描工件轮廓边界像素点序列中的横坐标值，找出最大值和最小值，按式（3）计算与工件轮廓相交的第一条平行线的横坐标值［6］.

（2）根据式（4）计算新的平行弦与工件轮廓的两个端点，判断是否需要拟合，如果不需要则执行第3步，否则执行第4步.

（3）计算下一条平行线的横坐标值，返回到第2步.

（4）按照式（4）计算每条弦求解出的圆心坐标和半径.

（5）判断a的值是否大于X的最大值，如果小于则返回第3步，否则直接退出.

1.3 等间距平行线算法流程图

基于栅格与等间距平行线原理算法，首先依次采集区域边界顶点的坐标，找出其中横坐标的最小值作为等间距平行线的初始值，同时按设定的精度值将整个区域栅格化，轮廓区域进行轮廓跟踪，求出区域的边界像素点.栅格单元划分的越细，尺寸参数计算效果越明显，引入一组等间距平行线，根据每条平行线与所有边界的交点来确定由该条平行线计算出的圆心和半径值，因为平行线间距大小均是一致的，所以可以很快在所有平行线条件下求解出圆心和半径值，整个过程完全由计算机程序自动完成，具体的算法流程如图1所示.

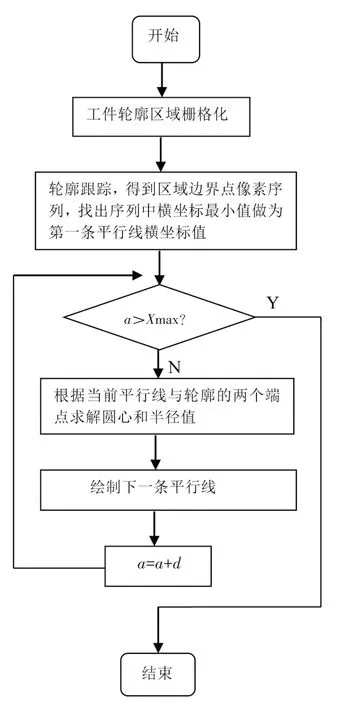
图1 栅格间隔为5个像素

2 基于等间距平行线检测圆

2.1 轮廓跟踪求解边界像素点序列

首先输入工件轮廓图，扫描工件轮廓边界像素点，依次读取轮廓所在栅格单元的行列值，建立边界像素点集合，如图2所示.

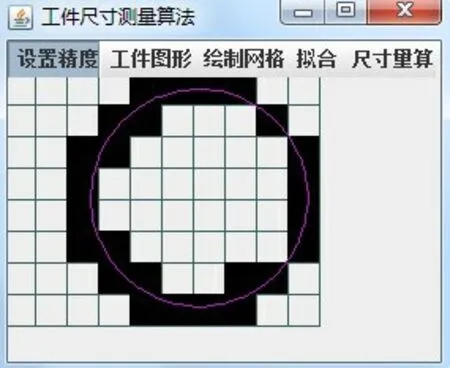
图2 栅格间隔为20个像素

根据图2可以计算出工件轮廓边界像素点序列，如表1所示.

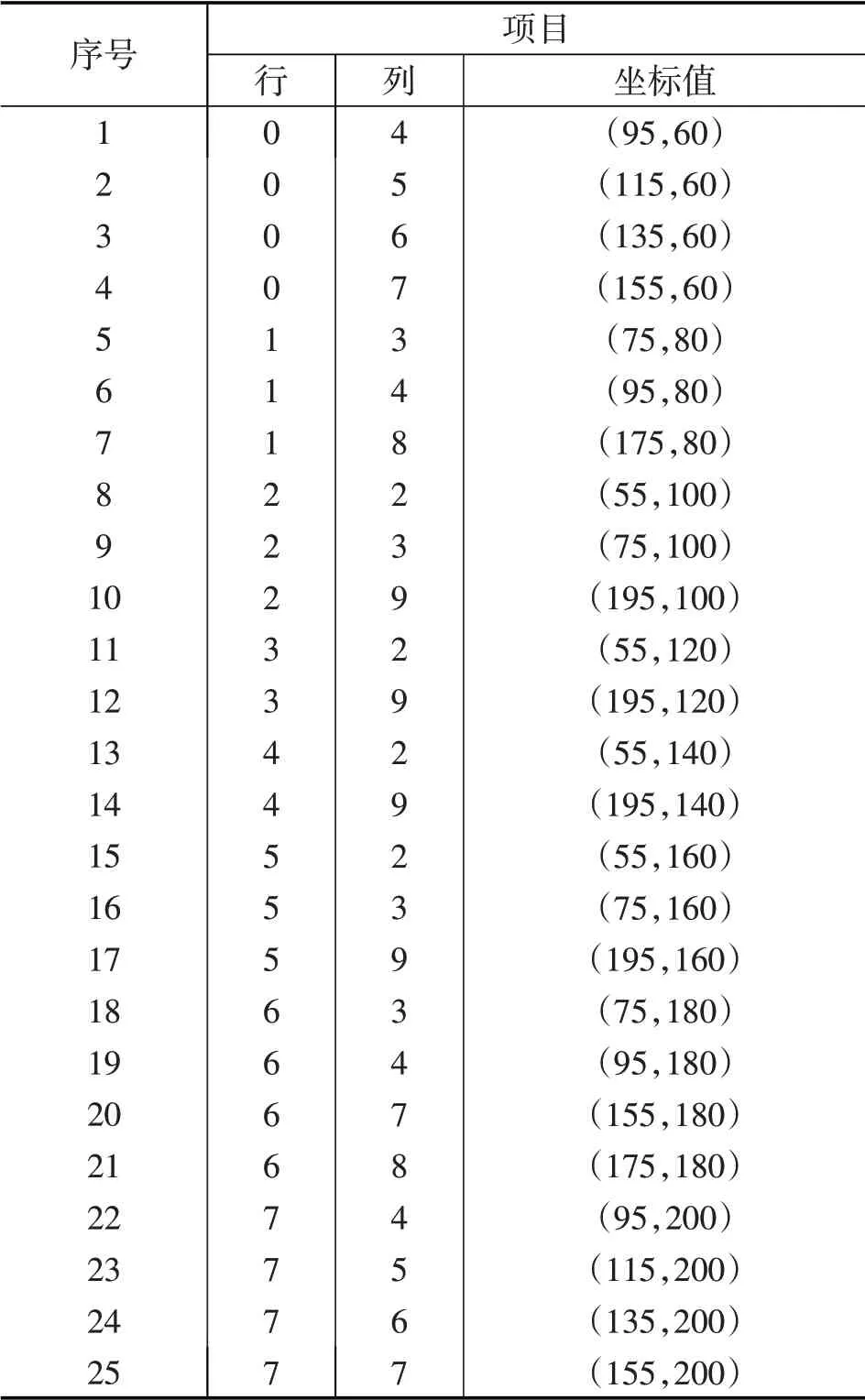
表1 工件轮廓对应的坐标值

表1中工件轮廓边界点的坐标值是以边界点所在的栅格单元中心点为准.

2.2 等间距平行线拟合圆

利用等间距平行线方法可以拟合圆，如图3所示，其原理是：搜索轮廓边界点像素序列，在工件轮廓内绘制一组等间距平行线，利用勾股定理计算每条弦与轮廓两个端点坐标.

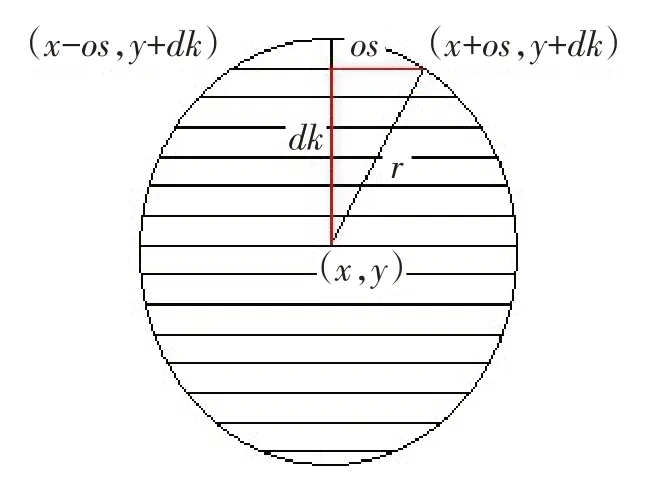
图3 等间距平行线与圆周的几何关系

在进行圆检测时，先从像素点序列中获取当前弦与轮廓两个端点的坐标值，根据端点坐标值计算出该条弦求解出的圆心坐标和半径，以此类推，当所有的平行线与轮廓端点求解出相应的圆心和半径值，与原始的圆参数对比查找出不同值，说明该条弦对应的端点需要拟合.

3 数据验证

3.1 刚性圈数据验证

圆测量是尺寸测量技术中应用较为广泛的测量方式，传统物理方式测量精度低，基于机器视觉技术则可以大大提高测量速度和精确度.图4（a）中内侧圆是标准的尺寸，外侧是产生了少许畸变的圆，对工件轮廓的区域栅格化，获取轮廓边界点像素点的值.

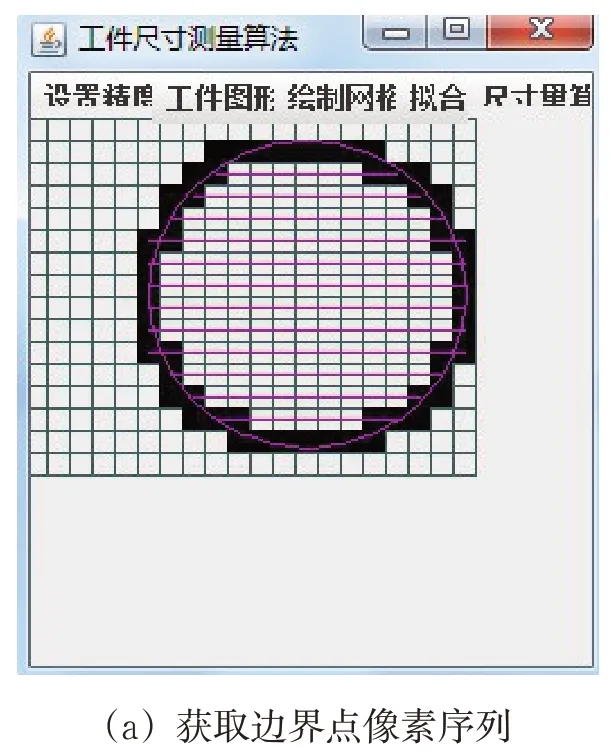
对工件轮廓区域栅格化，跟踪轮廓得到边界点的栅格单元值，以栅格单元中心点作为边界点的值，故边界点像素序列如下：

（90，65）、（100，65）、（110，65）、（120，65）、（130，65）、（140，65）、（150，65）、（160，65）、（80，75）、（90，75）、（160，75）、（170，75）、（180，75）、（70，85）、（80，85）、（180，85）、（190，85）、（70，95）、（190，95）、（60，105）、（70，105）、（190，105）、（200，105）、（60，115）、（200，115）、（60，125）、（200，125）、（60，135）、（200，135）、（60，145）、（200，145）、（60，155）、（70，155）、（190，155）、（200，155）、（70，165）、（190，165）、（70，175）、（80，175）、（180，175）、（190，175）、（80，185）、（90，185）、（100，185）、（160，185）、（170，185）、（180，185）、（100，195）、（110，195）、（130，195）、（140，195）、（150，195）、（160，195），根据边界点像素序列绘制一组等间距平行线，从序列中可以看出，在指定y值的平行线上有若干个像素点，弦与轮廓两个端点的值等于该条平行线的两个像素点的值，如y=155，两个端点分别为（60，155）、（200，155）.

利用勾股定理和每条弦与轮廓的两个端点坐标值计算圆心坐标和半径值，如表2所示.

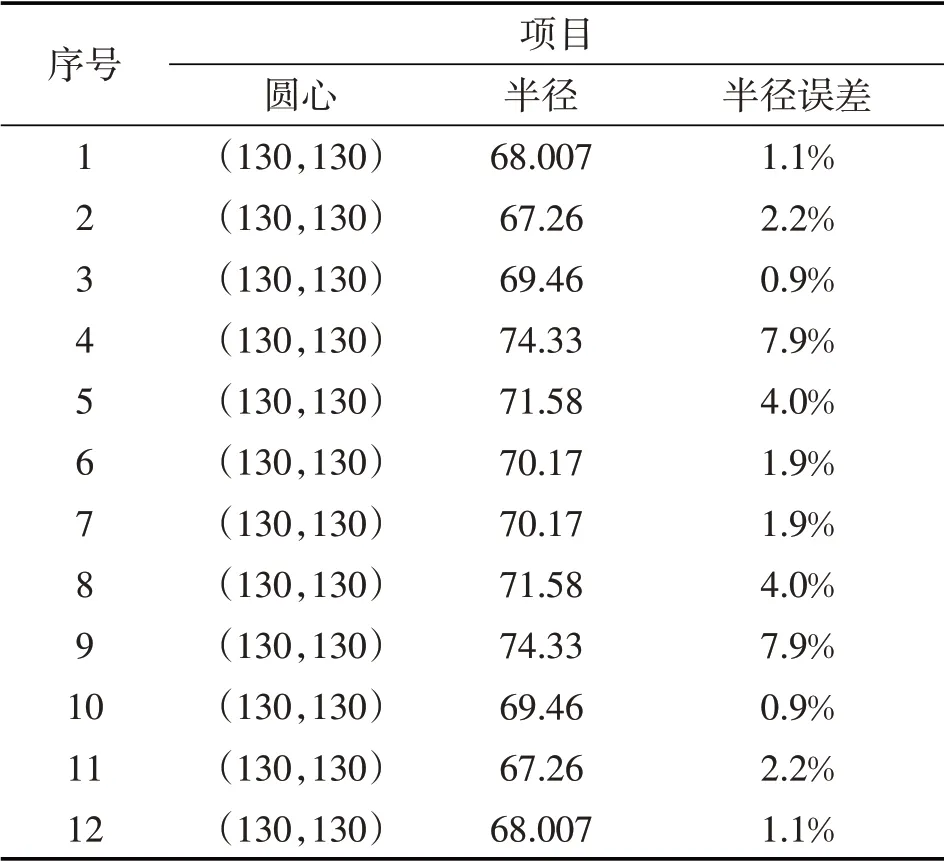
表2 刚性圈不同间隔值测量参数

圆的真实圆心为（128.83，128.83），半径值为68.83.从表2中可以看出，工件轮廓内有12条平行线，其中第3、10条弦计算出的半径值与实际值误差最小.由于在获取边界点像素序列是取栅格中心点坐标值，栅格宽度越小，精度越高，但计算量越大.在半径误差设定的阈值内，决定哪些端点需要拟合.拟合的方法是通过移动端点的栅格位置来调整.

3.2 圆的拟合

在表2中，第4条弦计算出的半径值误差最大，假设半径误差阈值为1%，此时，在图4（a）中，栅格宽度为10个像素单位，把第4条弦的右端点所在栅格单元向左移动一个单元，此时两个端点坐标为（60，105）、（190，105），重新计算半径值为69.64，半径误差为1.1%，虽然大于阈值，但精度有较大提高.此时还可以通过缩小栅格宽度，进一步提高精度值，经过拟合后的轮廓如图4（b）所示.

图4 工件尺寸测量

在图4（b）中，黑色轮廓是拟合后的效果图，栅格单元宽度为10个像素.

3.3 柔性密封圈数据验证

随着电子工业的蓬勃发展，橡胶产品正被越来越多的应用在更高要求的工业产品领域.橡胶密封圈、橡胶按键等都是很常见的配件，但橡胶零件的品质控制不像金属、塑胶材质的产品一样方便直接，因为橡胶产品本身是有弹性的、外力接触会发生形变，测量的时候传统接触式测量根本没办法实施.橡胶密封圈横截面是圆形，轮廓是内/外圆且往往因为形变等原因内外圆轮廓的尺寸会发生改变.对于密封圈内外圆半径值的测量，同样采用等间距平行线原理，首先对工件轮廓区域栅格化，分别识别出内外圆边界点像素序列，根据内外圆边界点像素绘制一组等间距平行线，取值时应保证内外圈像素处于同一线上，这样就可以保证同一条线与内外圈的各自两个端点都处于同一水平或垂直方向.设定半径误差阈值，根据勾股定理，分别计算每条弦对应的内外圈半径值.

3.3.1 误差分析

橡胶密封圈横断面通常是圆形，横断面的长度等于外圈与内圈差值，在对密封圈进行参数测量时，应在横断面的精度误差的范围内，同时也要把内外圈半径误差控制在阈值内.为了控制横断面和内外圈半径精度，在对内外圈拟合时，应根据每条弦计算出的内外径进行判断，如果外径偏差则拟合外圈，如果内径偏差则拟合内圈，这样可以控制横断面精度，如图5所示.

图5 密封圈尺寸测量

在图5中，标准的外圈半径值为68.83，内圈半径值为58.83，横断面宽度为10，根据勾股定理计算前6条弦结果如表3所示.

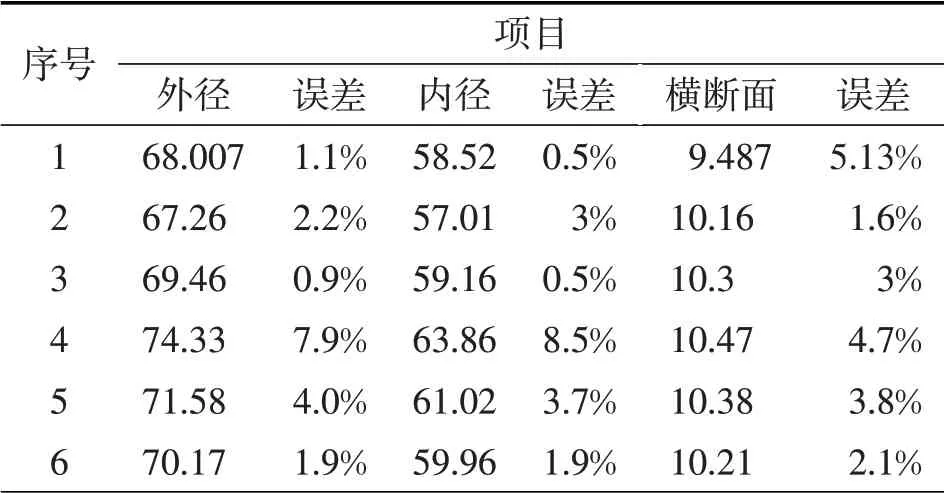
表3 柔性圈不同间隔值测量参数

造成误差的原因有以下两点：

（1）在对工件轮廓区域栅格化时，栅格单元的大小直接影响到测量精度，栅格越小精度越高，但计算量越大.

（2）传统的成像系统都会有少量的畸变，此时可以通过拟合圆来减少畸变对精度的影响.

3.3.2 算法复杂度分析

计算复杂度包括空间复杂度和时间复杂度.空间复杂度一般指存储量的问题，时间复杂度则是指计算的工作量问题［7］.基于多级格网辅助机器视觉曲面测量，随着网格划分越细，存储空间也会增大，但测量精度也提高.对于时间复杂度，由于该算法主要是判断栅格集合中每一个轮廓点行列值，采用多重循环语句结构，随着网格划分密度的增大，计算量会有所增加，但对于时间的复杂度影响有限.

4 结论

基于等间距平行线辅助机器视觉实现曲面轮廓参数测量，可以根据测量精度要求调整网格宽度大小，从而提高测量精度，在工程应用中具有一定的应用前景.