不平衡电网电压下双馈异步风力发电机组控制策略研究

陈凯杰，赵葵银，任晓红，唐勇奇，朱积嘉

（湖南工程学院 电气与信息工程学院，湘潭411104）

随着化石能源的不断枯竭，以风能为代表的可再生能源在世界能源中的地位愈显重要.近些年来，随着国家政策支持和商业价值的提升，风力发电在整个电力系统中的渗透率越来越高［1］.由于风力发电机组大多安装在风能资源丰富的偏远地区，其电网分支与主干电路距离远，电力系统维护不及时且难度大，易出现电网电压不平衡问题［2］.当电网电压不平衡时，采用PI控制策略的DFIG会出现输出功率和直流母线电压倍频波动的问题，影响DFIG的运行安全和可靠性.尤其对兆瓦级的大型风电场而言，不平衡电网电压下的输出功率和直流母线电压倍频波动，会极大地冲击电力系统，损坏电力设备，增加维护成本，甚至易造成安全事故［3］.因此平抑不平衡电网电压下的输出功率和直流母线电压倍频波动问题，成为亟待解决的技术难题.

国内外学者对于DFIG和变流器在不平衡电压下的运行控制做了大量的研究.文献［4］提出了一种典型的正、负序双d-q、PI电流控制方案，其基本方法是将不对称系统分解成正、负序对称分量，再实行各自的d-q轴解耦控制.文献［5］提出了一种扩展矢量控制策略，在双旋转坐标系下对双馈发电机转子电流的正、负序分量分别进行控制，取得了较好的控制效果，采用同样的方法用于不平衡电压下网侧变流器的控制.文献［6-7］提出了基于正转同步速旋转坐标系中比例积分谐振（PIR）电流调节器的矢量控制系统，在传统基于PI控制器的控制方法下引入谐振环节，针对二倍频脉动的负序分量进行消除，该方案优点在于无须对转子电流实现正负序分量分离，可对其进行统一调节且比例积分参数可按照传统PI调节器进行设计，有效保证了系统电流调节的精度和稳定的动态性能.

针对不平衡电网电压下的输出功率和直流母线电压的倍频波动问题，本文提出一种基于模糊-比例谐振控制器（Fuzzy-PR）的矢量控制策略，建立了不平衡电网电压下DFIG和网侧变换器的数学模型，通过仿真分析，突出Fuzzy-PR矢量控制策略在维持系统稳定上的优越性.

1 双馈异步风力发电系统的结构

双馈异步风力发电系统的结构如图1所示，DFIG通过齿轮箱与风轮机连接，将风轮机侧的低速旋转转化为高速旋转，进而实现风力发电.发电机的定子绕组直接连接电网，转子侧通过背靠背的双PWM变换器与电网相连，中间通过直流电容连接，进而实现交流励磁从交流到直流再到交流的转换［8］.

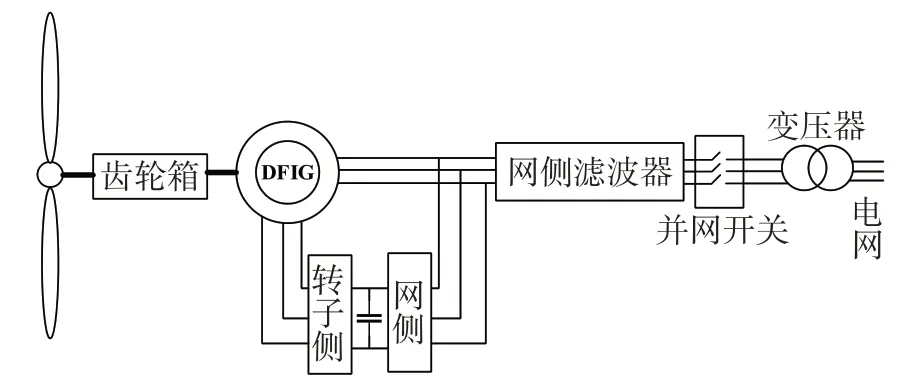
图1 双馈风力发电系统的结构图

2 电网电压不平衡时的DFIG风电系统建模

2.1 电网电压不平衡的DFIG建模

DFIG为三相三线制，其中点未与地面连接，处于断路状态，无须讨论零序分量对系统的影响，即可假设无零序分量，DFIG的等效电路可用正序电路和负序电路之和的形式表示.建立呈“T”形的正、负序等效电路模型，如图2所示.

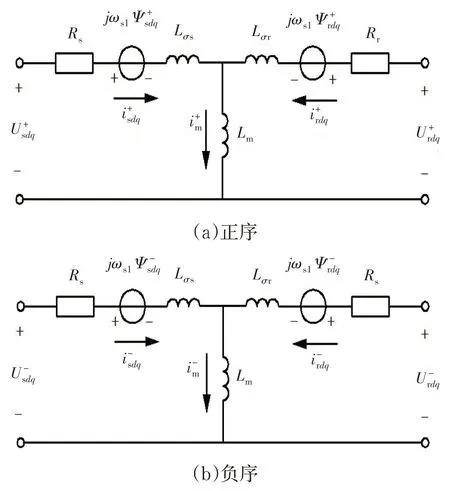
图2 DFIG的正、负序等效模型

参照三相平衡电压下DFIG的数学模型建立方法，将同步旋转坐标系d-q轴分为正d、q轴和负d、q轴，在基于正、负同步旋转坐标系上建立双馈异步风力发电机的电压方程和磁链方程［9］.

基于正序d-q坐标系，建立DFIG的正序电压方程和磁链方程：

1）电压方程

2）磁链方程

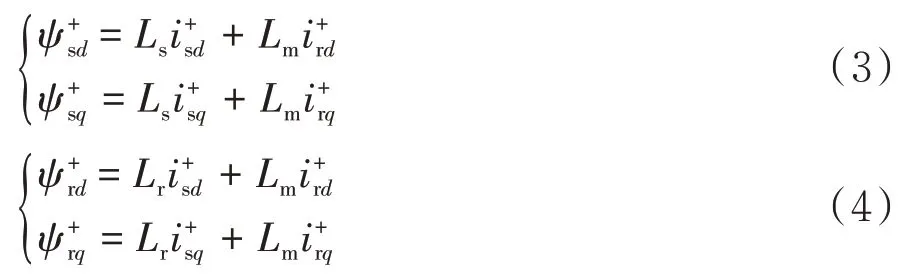
式中Lm为d-q轴定子、转子绕组的互感；Ls为d-q轴定子绕组的自感；Lr为d-q轴转子绕组的自感.式中各参数上标“+”号代表其为正序分量.

同理，基于负序d-q坐标系，建立的DFIG负序电压方程和磁链方程.各参数上标为“-”以代表其为负序分量.

2.2 电网电压不平衡的网侧变换器的建模

由于网侧变换器经滤波设备与电网直接连接，电网电压不平衡时，导致其运行性能受到影响.参照DFIG建模，网侧变换器的连接结构与DFIG同属三相三线制，因此其零序分量也可以忽略.建立不平衡电网电压下的网侧变换器的正、负序电路等效模型.

建立基于正、负序坐标系的网侧变换器模型，其正序d-q坐标系模型如式（5）方程式

同理，网侧变换器负序d-q坐标系模型与正序模型类似.各参数上标为“-”以代表其为负序分量.

3 电网电压不平衡时的DFIG风电系统控制

电网电压处于不平衡状态时，传统控制策略下的双馈风机系统会出现电机三相绕组不均匀发热、引发过电流现象；与电网直接相连的网侧变换器交流侧引入负序电流，直流侧存在倍频波动；电机有功功率、无功功率和电磁转矩中存在二倍频波动，严重影响系统的安全稳定运行［10］.

传统控制策略难以对电网电压不平衡时的风电系统进行有效控制，因此提出基于Fuzzy-PR的控制策略来解决传统控制方式产生的倍频波动问题.

3.1 基于Fuzzy-PR控制的转子侧变换器控制系统设计

电网电压不平衡时，对转子侧变换器而言，其能用于控制的变量有.根据式（1）到式（4）中电网电压不平衡时的DFIG正序数学模型，令原式中的ωe=0，进而得到两相静止坐标系下的电机电压和磁链表达式：

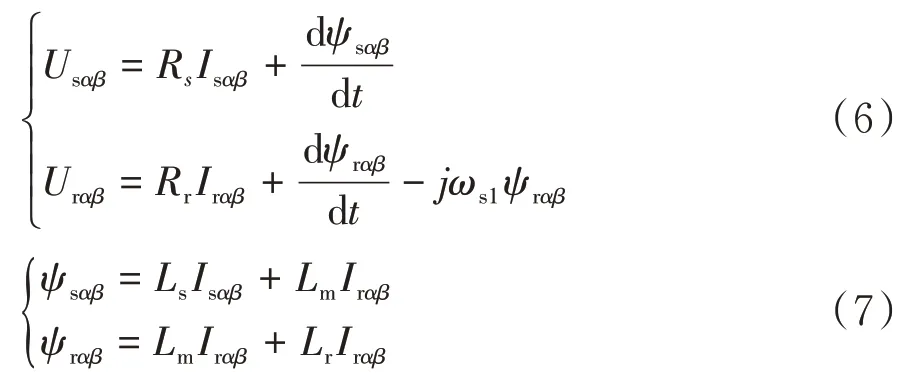
式中，Usαβ、Urαβ为定、转子α-β轴的电压；Isαβ、Irαβ为定、转子α-β轴的电流；ψsαβ、ψrαβ为定、转子的α-β轴的磁链.

根据上述式子，可建立两相静止坐标系下DFIG等效电路，如图3所示.

图3 两相静止坐标系下DFIG等效电路图

根据DFIG等效电路，得到基于α-β坐标系的不平衡电网电机转子电压方程式：

由于电网电压在不平衡时，转子电流可分为角频率为ω0的正序和负序的电流分量，如式（7）所示.因此可以利用PR控制器来对转子电流分量进行统一的调节.通过对Irαβ的求导，可得基于转子侧的准PR控制器在α-β坐标系上输出的控制电压参考值可通过准PR控制器设计为：

其中

式中krp、krr为转子侧PR控制器的比例、谐振系数，ωr1为转子侧PR调节器的截止频率.

建立电网电压不平衡条件下的转子侧变换器控制系统，如图4所示.1

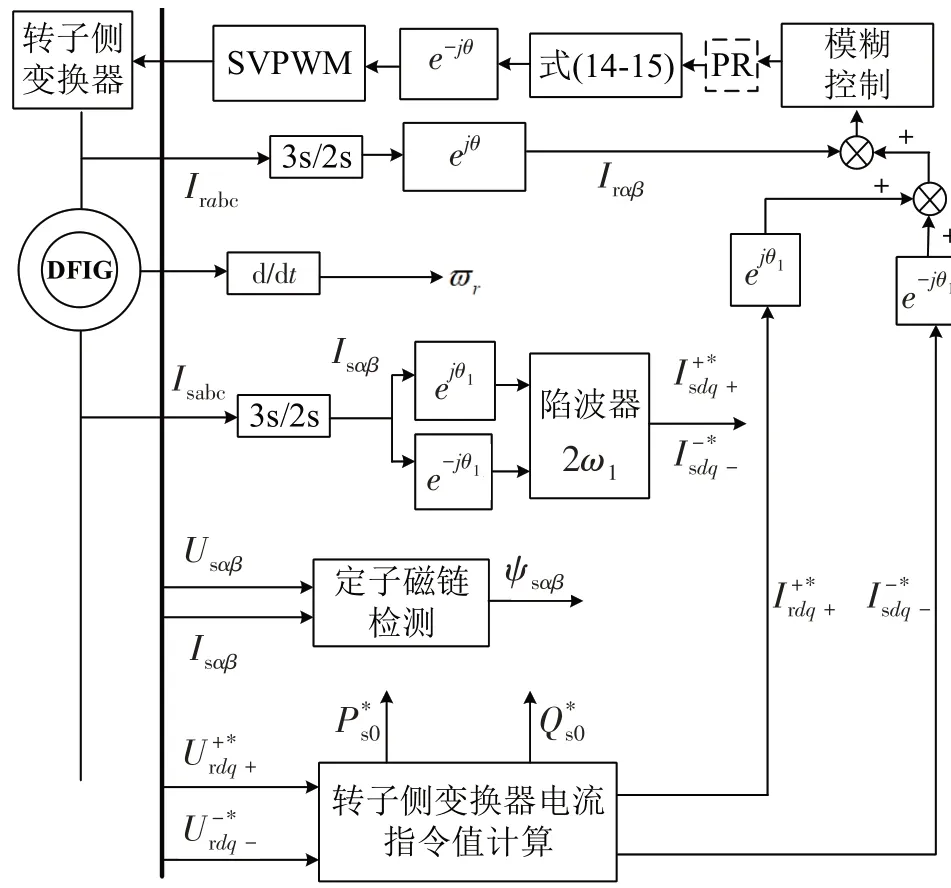
图4 转子侧变换器控制系统框图

3.2 基于Fuzzy-PR控制的网侧变换器控制系统设计

电网不平衡下的网侧变换器，交流侧有功、无功功率均出现了二倍频脉动，可参考电流为和.根据网侧变换器的数学模型建立不平衡电网电压下的网侧变换器数学模型，令原式中的ωe=0，可得到两相静止坐标系下的网侧变换器电压表达式为：

将上式写成矢量形式为：

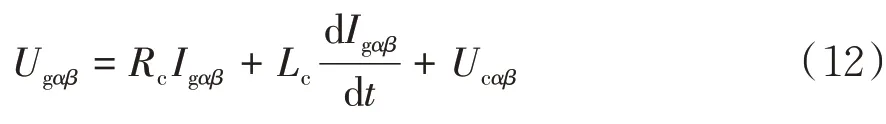
对Igαβ进行求导，可得基于网侧PR控制器在α-β坐标系上输出的控制电压参考值通过PR控制器调节可得到：

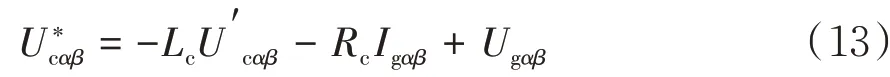
其中：

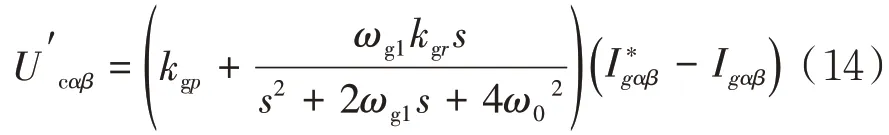
式中kgp、kgi、kgr为网侧PR控制器的比例、积分、谐振系数，ωg1为网侧PR调节器的截止频率.

建立电网电压不平衡条件下的网侧变换器控制系统，如图5所示.

图5 网侧变换器控制系统框图

4 仿真模型的建立与分析

4.1 仿真模型的搭建

根据图1所示的双馈异步风力发电系统结构图，结合DFIG和网侧变换器不平衡电网电压下的数学模型和本文提出的基于Fuzzy-PR的控制策略，通过Matlab/Simulink仿真平台，搭建双馈异步风力发电系统的仿真模型.

电机内部参数设置：电机额定功率为1.5 MW，额定频率为50 Hz，磁极对数为3，定子电阻和转子电阻设置为0.023 pu、0.016 pu，定、转子互感为2.9 pu，定子和转子的漏电感设为0.18 pu和0.16 pu.直流母线电压设为1200 V，直流电容设为18000μF，网侧变换器等效电感设为2 mH，等效电阻设为0.01Ω.

针对不平衡电网电压下，电流负序分量导致系统的不稳定波动，提出Fuzzy-PR控制策略，实时整定控制器参数，消除负序电流分量.

4.2 仿真分析

在0 s到1.5 s接入理想电网电压，电网电压对称平衡.在1.5 s到4 s设置A相电压跌落，为便于观察改进控制策略的效果，将不平衡度设置为5%.在0 s到2 s内，仿真采用传统基于PI的矢量控制策略；2 s到4 s采用基于模糊-谐振控制的矢量控制策略，通过对比，更能直观的分析仿真结果.设置电网电压仿真波形如图6所示.

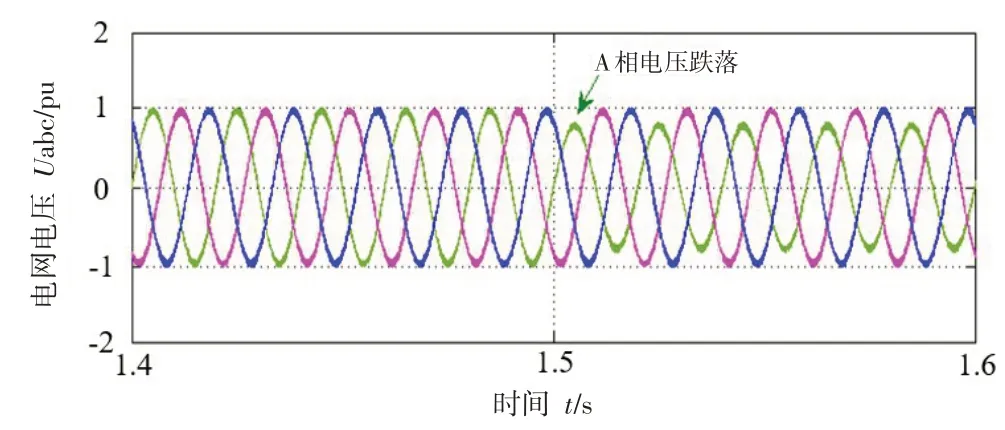
图6 电网电压仿真图

如图6所示，1.5 s时电网电压发生不平衡，发生电压跌落现象.因此在2 s时引入本文的改进控制策略，通过陷波器提取正序电压.d-q坐标下的定子电压u sdq，如图7所示.

图7 d-q坐标系下定子电压u s dq仿真图

其中d轴、q轴的定子电压正、负序分量仿真图，分别如图8、图9所示.

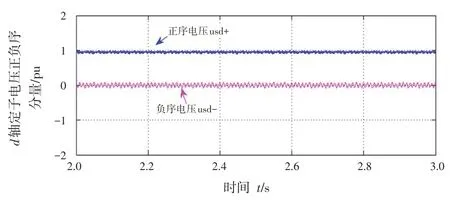
图8 d轴定子电压正负序分量仿真图

图9 q轴定子电压正负序分量仿真图

分析图8、图9，在电网电压不平衡的系统中，前1.5 s采用传统控制策略下的仿真波形出现较为明显的失真，2 s后，由于采用改进的控制策略，在短时间的过渡后，消除负序电流的影响，波形趋于稳定.

图10、图11分别为转子和定子电流仿真图.

图10 转子电流仿真图

图11 定子电流仿真图

分析图10、图11，在1.5 s到2 s采用传统控制策略下的转子和定子电流波形出现明显的失真现象，倍频脉动明显.2 s后使用本文提出的基于Fuzzy-PR控制的策略，对波形进行迅速调节，在极短的时间内稳定波动，很好地消除了负序电流的影响，波形逐渐趋于平衡对称.

分析图12，在1.5 s时由于电压跌落，传统策略下的功率波形呈现出明显的振荡；在2 s时采用改进得控制策略，振荡明显减弱.

图12 有功和无功功率仿真图

通过对比，本文提出的基于Fuzzy-PR的控制策略可以有效地平抑不平衡电网电压下DFIG产生的输出功率和直流母线倍频波动，保证系统的稳定运行.

5 结论

针对电网电压不平衡时，采用传统PI控制策略的DFIG风电系统的输出功率和直流母线电压出现倍频波动问题.本文通过对不平衡电网电压下的数学模型分析，建立基于Fuzzy-PR控制策略的控制模型，通过仿真分析验证了本文的改进控制策略可以较好地对倍频波动进行控制，保证电网的安全稳定运行.