项目驱动的Python编程教学设计
钱逸舟 方璐


项目驱动式教学的理念一经提出便在全球范围内获得广泛关注,不同的国家和地区纷纷根据本地的教育现状对项目驱动式教学进行本土化尝试。项目驱动式教学重视从真实情境中提取驱动型问题,将学科内容与真实问题解决情境有机整合,旨在锻炼学生的高阶思维与问题解决能力,这与我国新课改理念不谋而合。以信息技术课程为例,《普通高中信息技术课程标准(2017年版)》提出,信息技术课程要注重培养学生的信息素养、问题解决能力等多种高阶思维。同时,当前高中信息技术课程中越来越多地引入Python编程作为教学内容,而项目驱动式教学便是帮助学生综合使用已经学到的Python编程知识,锻炼问题解决能力的一种教学方式。因此,根据驱动式教学理念对高中信息技术课进行重构具有可行性和必要性。本文将以“蒙特卡洛法求圆周率”一课为例,介绍此类教学的主要流程。
● 前期分析,选择项目
项目驱动式教学的核心在于寻找一个合适的探究项目。笔者认为,一个好的探究项目应具有以下特点:①项目解决的是一个真问题,具有真实的生活或学科背景;②项目的难度和内容适合本年龄段学习者的能力;③项目具有可探究性,问题的结论通常无法直接获得,需要经过科学实验或计算机建模等手段推导得出。
本文选择的“蒙特卡洛法求圆周率”问题就符合以上特点。首先,蒙特卡洛法求圆周率指的是在单位正方形内构造单位圆,随后在整个区域内投点,根据落在圆内的点数与投点总数的比值求出圆周率的方法,其中,为保证精确,投点总数通常较大,因此计算落在圆内点数显得较为困难,此时就可以自然引入计算机模拟的方式协助探究。学生在探究过程中,既可以复习学科知识,又能够锻炼问题解决和高阶思维能力。其次,本项目并非零散的知识拼接活动,而是对已学知识的有机整合与灵活运用。在本项目中,学生将运用Python编程中的循环结构、选择结构、随机模块(Random)以及计算函数等知识点,解决依托于真实情境的问题,检测自身对Python编程的掌握程度。因此,本项目是一个非常好的能够帮助学生学以致用的项目。需要指出的是,蒙特卡洛方法同时也是一种经典的统计学方法,在使用蒙特卡洛法解决问题时,学生也可以同时锻炼数学学科中的“概率与统计”单元的内容,一举多得。
如图1所示,本项目在教学中主要经过“问题导入,激发动机——梳理流程,测试程序——拓展问题,自主探究”三大步骤,下面详细介绍具体的流程。
● 导入问题,激发动机
在正式教学前抛出导入问题,有助于激发学生的学习动机,调动课堂学习积极性。以“蒙特卡洛法求圆周率”为例,教师可以邀请学生一起回忆之前学习的与圆周率有关的内容,随后让学生思考并讨论以下问题:提供一个直径为1的圆,怎样尽可能精确地求得圆周率的值?学生自由讨论约3分钟后,请想出不同方法的学生介绍自己的想法,并穿插介绍如“割圆术”“测量法”等多种方法。接着,教师在单位圆外做外接正方形,可得圆面积为圆周率除以4,正方形面积为1,那么圆面积与正方形面积的比值为圆周率除以4。也就是说,只需要找到另一种可以代表圆面积与正方形面积比值的方式,就可以求出圆周率的值。
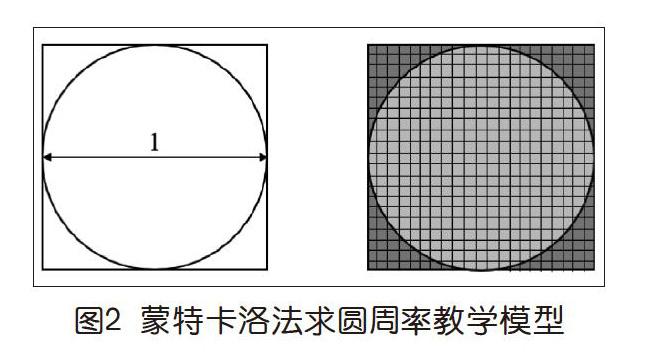
隨后,教师展示如图2所示的教学模型,从模型中观察可知,圆的面积可以用圆内小正方形的数量表示,而外接正方形的面积则等于总 的小正方形数量。同时不难看出,总的小正方形数量N是影响结果的关键值,N越大,小正方形越趋于一个点,得到的圆周率值越准确。因此,可以将无限缩小的小正方形比作一个个小点,推导可得到如图3所示的等式。推演过程不需要所有学生掌握,学生只需要了解推演结果即可,在后续的编程训练中会继续深入学习。
● 梳理流程,测试程序
在介绍完蒙特卡洛法求圆周率的数学推导过程后,邀请学生尝试使用蒙特卡洛法在白纸上测算圆周率的近似值,随后思考自己使用蒙特卡洛法求圆周率的流程,画出流程图。这一步可以帮助学生进一步理解知识点,同时也可以把复杂的过程分解为可编程的子问题。同时,在纸上推演得到的圆周率值通常与真实的圆周率值相差较大,因此可以自然引入Python编程进行更为精确的模拟。在这一环节中,蒙特卡洛法求圆周率问题可以被分解为三个子问题:①如何用代码模拟在单位区域内投点的过程?②如何计算圆内的点的数量?③如何将圆内的点的数量转化为圆周率值?
在明确问题的分解与模型的抽象后,教师需要引导学生结合学习过的Python编程知识,将先前绘制的流程图转化为如图4所示的示例代码。其中,子问题一可以采用Random函数产生随机数代表投点坐标;子问题二可以结合数学知识,如果投点的坐标到原点距离小于1,则证明投点位于圆内,同时结合判断和循环语句完成多次计数;子问题三则采用换算公式完成。学生此时不需要写出具体的代码,只需要针对流程图对程序简单勾勒。
● 拓展问题,自主探究
在完成对程序的简单设计后,学生可以上手进行编程。此时教师要注意,虽然学生已知晓程序的主要结构,但由于学生对知识点的掌握程度以及自身能力不尽相同,应根据个体差异性为不同的学生布置不同的任务。对学习基础较好的学生,可以只提供函数名称和输出部分的内容;对学习基础较薄弱的学生,可以采用“填空”的形式,如抹去第10行与第8行代码,只要求写出重点代码即可。
对学习基础较好的学生,应当鼓励其进行更深层次的探究。此处的探究方向有二:其一,可以将程序作为探究圆周率值的实验工具,鼓励学生改动重复次数,画出“圆周率值—重复次数”的函数图像,对蒙特卡洛法有更深入的了解;其二,布置学习迁移任务,学习迁移任务的难度不应过高,应与本节课知识紧密相关,同时在学生的最近发展区内。本例中采用“套环为什么总是套不中”这一案例作为提升学习的问题。下面对套环问题进行简单介绍。
套环问题来源于真实的生活情境:在生活中随处可见的套环游戏,规则是将套环整个套中设定的物体就算胜利。它听上去非常简单,但事实上的胜率总是不理想。这其中是否暗含着一些数学或科学原理?可以将套环问题视为如图5所示的数学模型,假设以原点为中心、直径为1的圆为需要套中的物体,设定直径为2的套环。套环是否套中物体就可以看作套环的圆心到物体圆心(原点)的距离是否在[0,1/2)的范围内。根据蒙特卡洛方法,只要重复次数足够多,就可以得到较为准确的投中物体概率值。
● 总结
本文以“蒙特卡洛法求圆周率”一课为例,介绍项目驱动式的信息技术课的主要实施流程。总体来说,项目式学习主要包括“导入—流程—程序—拓展”四个步骤,而Python只是作为辅助建模与实验工具。与此同时,笔者认为,项目驱动下的信息技术课堂若要具备可实施性,可以尝试深度整合其他学科,针对其他学科课标内的重难知识点进行扩充与复习,如本文中介绍的信息技术与数学学科的整合案例。这样设计出来的课程不但对信息技术学科的学习有帮助,而且可以反哺于其他学科的掌握。当然,由于笔者并未进行教学实践,本文的观点也不过一孔之见,期待未来有更多优秀的信息技术整合其他学科的教学案例可供参考。

