频率稳定约束条件下风电并网能力的确定方法

谢 岩，马世英，唐晓骏

（电网安全与节能国家重点实验室（中国电力科学研究院有限公司），北京 100192）

近年来，我国风电装机容量的不断攀升，使得电网格局发生重大变化，也对电力系统的惯量水平和频率特性造成了显著影响。双馈感应发电机DFIG（doubly fed induction generator）作为应用最为广泛的风力发电机型，具有转子转速与电网频率解耦的特点，无法响应电力系统频率的变化，不具备调频能力[1-2]。因此，在风电高渗透条件下，电网频率稳定问题日益凸显，并成为制约风电并网容量的主导约束因素，迫切需要开展电网频率稳定约束下新能源并网能力的评估方法研究。

分析风电接入对系统惯量水平的影响是研究含风电系统频率稳定性的关键和前提，部分文献对此开展了研究。文献[3]计及风电和负荷的波动概率，建立了一种考虑风电接入比例对系统惯性时间常数影响的概率模型，进而对风电并网对于系统调频体系的影响进行了定量分析；文献[4]考虑到风机接入替代同步机的情况下，系统中同步机装机容量随之下降，得到惯性时间常数随风电接入比重递减的结论；文献[5]定性地分析了风电并网对同步机的不同影响情况下对系统惯量水平的冲击，但没有给出定量关系的推导。文献[3-5]的分析在一定条件限制下都有一定的合理性，但分析过程考虑因素不够全面。

随着风电并网比例的提高，频率的暂态变化率增加，造成最大频率偏差加大，系统抵抗扰动的能力不断减弱[6]。文献[7]以火电机组的频率特性模型为基础，指出当由风速变化等因素造成风功率的波动值达到5%时，会引起电网的频率变化1%；文献[8]以负荷扰动期间系统的稳态频率偏差不超过±0.2 Hz为限制条件，以IEEE39节点系统为例，得到了系统可承受的最大风电并网比例；文献[9]以某电网数据为基础，通过仿真分析了系统出现不平衡功率情况下，频率偏差达到0.5 Hz 时的新能源占比。文献[7-9]均以仿真结果为依据，给出了一些具有指导意义的定性结论，但是由于缺乏严格的理论推导，其适用范围有失一般性。

本文提出了一种在频率稳定约束条件下确定风电并网能力以及合理替换同步机比例的量化分析方法。从理论上推导风电并网系统的等值惯性时间常数和同步机单位调节功率表达式，以及衡量系统暂态频率响应指标与风电渗透率和替换同步机比例的关联关系，在此基础上依据电力系统对电网最大频率跌落值和稳态频率偏差指标的要求，研究电网频率稳定约束制约新能源并网能力的机制，以实现量化评估电网对新能源的承载能力和合理的风机替换同步机比例。

1 电力系统频率变化特性

电力系统频率调节作为闭环控制系统，主要包括发电机组、负荷、汽轮机及其调速器。研究电力系统的频率特性一般不考虑系统各节点频率变化差异与功角稳定问题。当出现功率缺额导致系统频率发生变化时，发电机的调速器和负荷将参与有功平衡，频率暂态变化特性可列写为

2 风电并网系统的频率响应变化特征

DFIG 的定子直接与电网相连，转子通过励磁变换器进行交流励磁，其采用变速恒频运行方式进行最大风能追踪控制，通过调节转子的励磁电流，确保风电机组输出频率的恒定且不受电网频率变化的影响。这种与电网的柔性连接特性，使得风机不能像同步机那样参与电力系统频率响应过程中的惯性响应。因此在分析风电并网系统的惯量和频率变化特性时，可以将风机作为功率注入源处理。

2.1 风电并网系统的等值惯量特性的变化

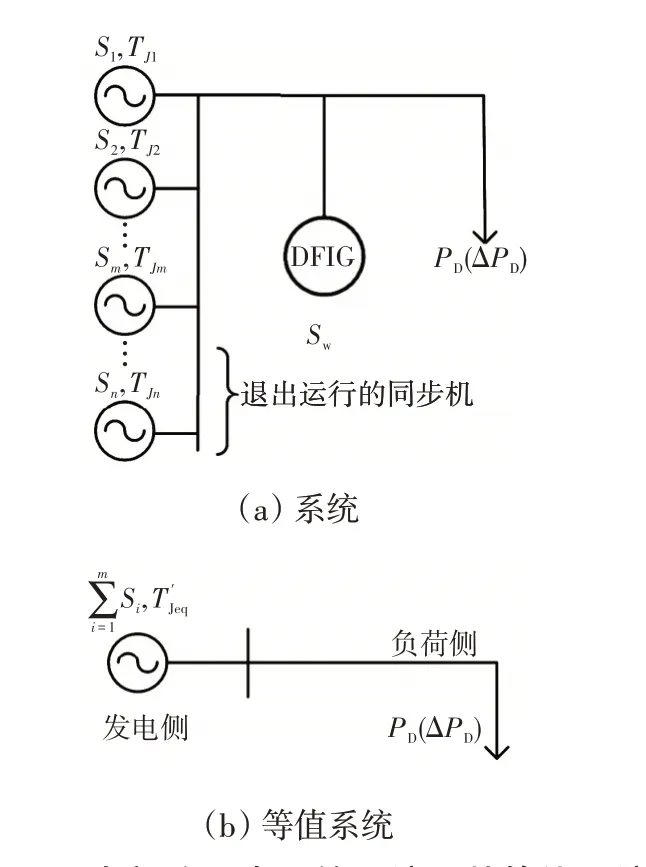
图1 退出部分同步机的系统及其等值系统Fig.1 System and its equivalence after cutting off part of synchronous machines

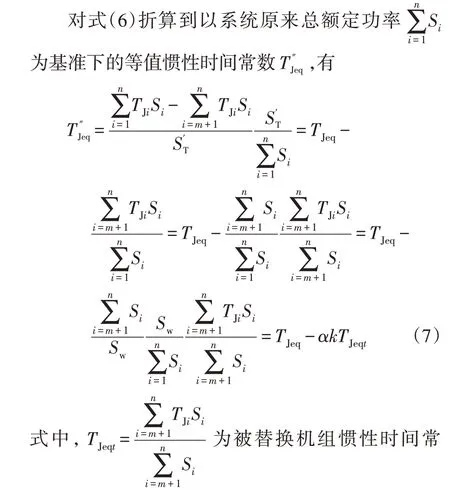
2.2 风电并网系统的机组功率调节能力的变化

考虑风电并网后，在切除部分同步机而剩余m台机组改变出力时，机组等值单位调节功率在标幺值体系下的计算公式为

同样地，随着风电渗透率的提高，等值机组单位调节功率会随之削弱，不利于系统频率的恢复，增大了稳态频率偏差。另外对于仅影响同步机出力的情况，风电并网不会对系统等值同步机的单位调节功率产生影响，因而同步机组的一次调频能力不变。

2.3 风电并网系统的频率响应指标量化分析

根据系统频率响应的过程的动态变化特征，本文从扰动发生时刻的初始频率变化率、最大频率跌落值和稳态频差3 个衡量系统频率响应的指标对风电并网系统的暂态频率变化进行量化分析。

2.3.1 初始频率变化率

在系统出现功率失衡ΔPL的情况下，系统的加速转矩可用系统总惯量与角加速度Δα的乘积来表示，可得

可以看出，系统的频率的初始下降速度主要由系统总的惯量大小决定，惯性能力强对应的等值惯性时间常数就大，将延缓频率下降的速度。但是，风电并网削弱了系统的惯量特性，加快系统的频率变化率，对系统的频率稳定带来不利影响。另外，并网比例k相同时，随着替换比例α的提高与被替换部分同步机惯量水平TJeqt的增大，对初始频率变化率的影响逐渐增大。

2.3.2 电网最大频率跌落值2.3.3 稳态频差

风电并网前后的系统稳态频差(Δf∞(t))be和(Δf∞(t))af之比为

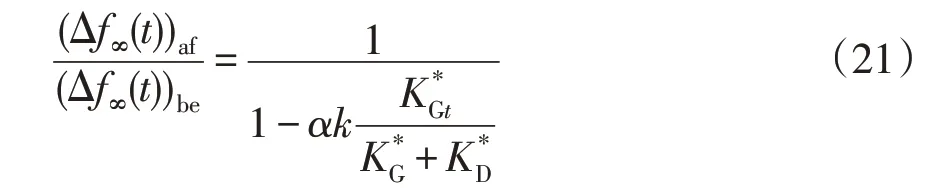
可见，风电接入比例k相等的情况下，系统稳态频率偏差会随着替换比例α的增加而增大，同时所替代部分同步机的单位调节功率越大，对稳态偏差的影响也会越大。

3 考虑频率稳定约束的风电并网能力确定

为提高风电渗透率系统的运行经济性，有必要使风电对原有同步机进行合理替代。由前面分析可知，这势必会使系统的惯量水平以及一次调频能力下降，亦即TJeq与K*G随α、k的提高而衰减，反映系统频率暂态响应特性的关键指标Δfmax与Δf(t∞)也随之恶化，使电网频率稳定问题凸显，并成为制约新能源并网容量的主导约束因素。电网运行准则规定系统需满足最大频率跌落值不超过1.0 Hz 且稳态频率偏差不超过0.2 Hz，即Δf(t∞)≤0.2 Hz。为了保证高风电渗透率电网的运行安全，合理确定电网频率稳定约束下风电并网能力是关键。

本文给出一种在频率稳定约束条件下确定风电并网能力的方法。首先从理论上推导出风电接入比例k和同步机的替换比例α与Δfmax、Δf(t∞)的关联关系，以满足电网最大频率跌落值和稳态频率偏差不越限为约束条件，计算出可以等容量替换同步机的风电接入最大值（或临界值）kcri以及风电接入比例k和同步机替换比例的制约关系，基于此可以确定与任意风电渗透率相适应的合理替换同步机的比例α，使高风电渗透率电网并网能力的量化评估得以实现。

3.1 考虑最大频率跌落值约束的风电并网能力

由式（7）、式（9）及式（19）可知，最大频率跌落值是关于α和k的函数，在频率稳定约束下两者存在如图2所示关系，其反映了最大替换比例αmax1随风电渗透率的提高而变化，显然同步机替换比例须满足α≤αmax1。根据式（22）可得等容量替代的临界比例kcri1，当风电并网比例k≤kcri1时，风电等容量替代同步机不会使最大频率跌落值越限，即αmax1=1。但当风电渗透率不断提高，当k>kcri1后，为保证运行安全性，不能再等容量替代，要减少风电替换同步机的容量，即αmax1随之减小，αmax1与k将受到式（22）约束，且满足

因此，当风电接入比例越过临界值kcri1后，按照频率稳定约束要求，可以按照式（21）合理地确定出同步机最大替代比例αmax1。

3.2 考虑稳态频率偏差约束的风电并网能力

同样，风机并网后，系统的等值发电机单位调节功率变为K*G″，且它与α、k有关，系统频率恢复的稳态频差因α、k变化而变化。考虑稳态频率频差这一约束条件后，有

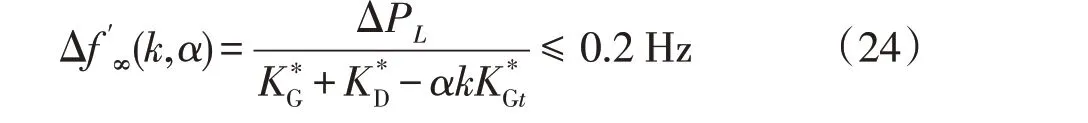
由式（7）、式（9）及式（20）可知，稳态频率偏差也是关于α和k的函数，在频率稳定约束下两者仍存在如图2所示的关系。

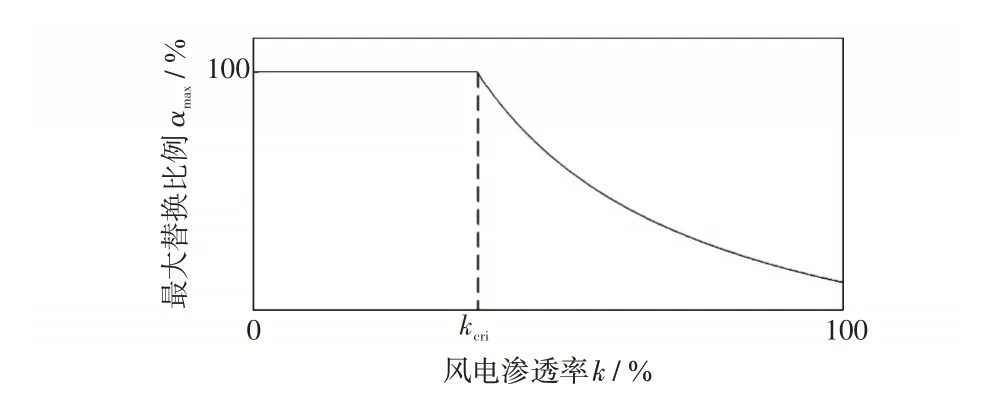
图2 最大替换比例与风电渗透率的关系Fig.2 Relationship between maximum replacement ratio and penetration rate of wind power

针对考虑稳态频率偏差约束的分析过程与考虑最大频率跌落值约束的分析类似，这里不再赘述。根据式（24）可求得在稳态频率偏差约束下等容量替换同步机的临界比例kcri2。当风电并网比例k≤kcri2时，风电等容量替代同步机不会使稳态频率偏差越限，即αmax2=1；当k>kcri2时，αmax2与k将受到约束，且满足

以此关系可确定风电接入比例越过临界值kcri2后对应的同步机最大替代比例αmax2。

3.3 考虑频率稳定约束的并网能力的确定

在分别分析了最大频率跌落值和稳态频率偏差约束条件下风电并网能力的基础上，为保证系统安全稳定运行，2个约束条件需要同时满足规定要求，可以确定风电并网的最大等容量替换比例kmax为

为提高含风电系统的运行经济性，希望尽可能实现等容量替代同步机，但是一定要以保证电力系统安全运行为前提，也就是说，当k≤kmax时，等容量替代同步机能够兼顾安全性与经济性。但当并网比例k>kmax后，由于不能再对同步机进行等容量替代，经济问题将成为制约风电并网规模的重要因素。此时替代同步机最大比例αmax可以依据kmax来确定，即

因此，在新能源系统规划中，可以在保证安全性的条件下，综合考虑风电并网给系统带来的附加投入与同步机减少发电量所节约的成本，确定系统中新能源可以并网的容量。

4 仿真分析

本文以三机系统为例进行仿真来验证所提分析方法的正确性。选取的3 台同步机的额定容量均为200 MW，等值惯性时间常数均为6.0 s，所接入系统风电场的单台风机额定容量为1.5 MW，2个负荷分别为200 MW和250 MW。设在1 s时的有功缺额为18 MW。所考虑的系统频率稳定约束条件如下。

约束条件1：系统最大频率跌落值约束。依照电网运行准则取1.0 Hz，考虑裕度时取0.8 Hz；

约束条件2：系统稳态频率偏差约束。依照电网运行准则取0.2 Hz。

4.1 风电并网等容量替换同步机

风电并网后通过减少同步机的出力实现功率的重新平衡。当风电并网等容量替换同步机时，除被替换同步机外其余同步机出力不改变，仅通过同步机退出实现功率的重新平衡。

（1）考虑约束条件1。等容量替换时αmax1=1，最大频率跌落值约束1.0 Hz 所对应的风电渗透率临界值为kcri1=38.3%。频率响应时间变化过程如图3所示。若风电渗透率进一步提高，最大频率跌落值将超过1.0 Hz的约束限值。图4示出了最大频率跌落值随风电渗透率的变化情况。若考虑一定裕度以确保不至于引起低频减载装置动作，将最大频率跌落值的约束缩小至0.8 Hz，可求得同步机等容量替换的风电接入临界值为21.6%。

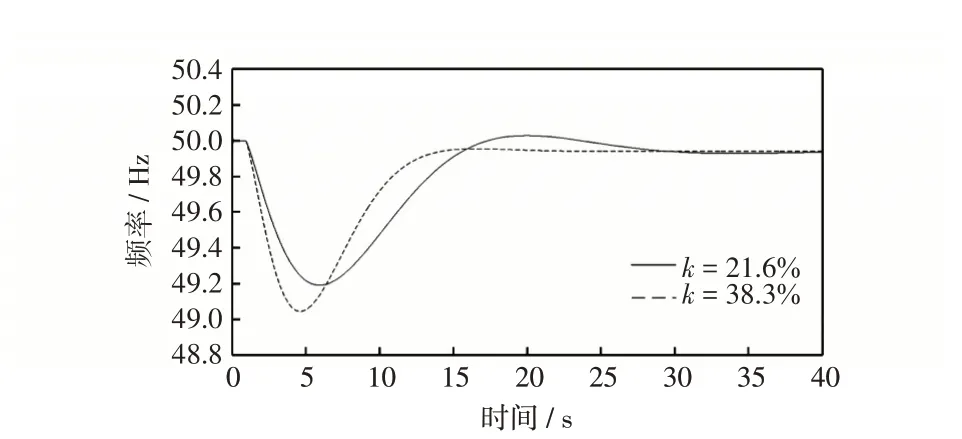
图3 约束条件1 下等容量替换同步机频率响应曲线Fig.3 Frequency response curve of equal capacity replacement synchronous machine under constraint 1

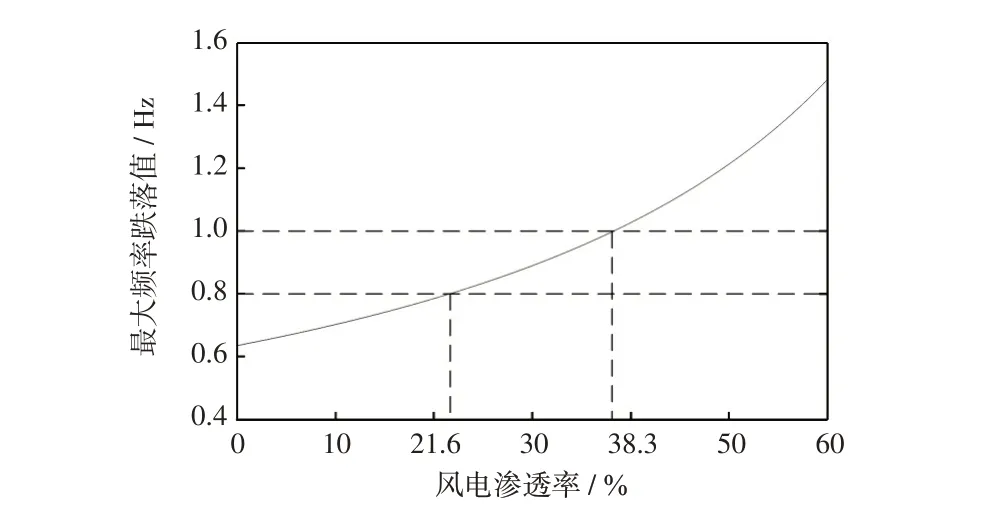
图4 最大频率跌落值与风电渗透率关系Fig.4 Relationship between maximum frequency drop and penetration rate of wind power

（2）考虑约束条件2。等容量替换时αmax2=1，稳态频率偏差约束为0.2 Hz 所对应的风电渗透率临界值为kcri2=67.5%。频率响应时间变化过程如图5所示。若风电渗透率进一步增大，稳态频率偏差将超过0.2 Hz 的约束限值，图6 为稳态频率偏差随风电渗透率的变化情况。

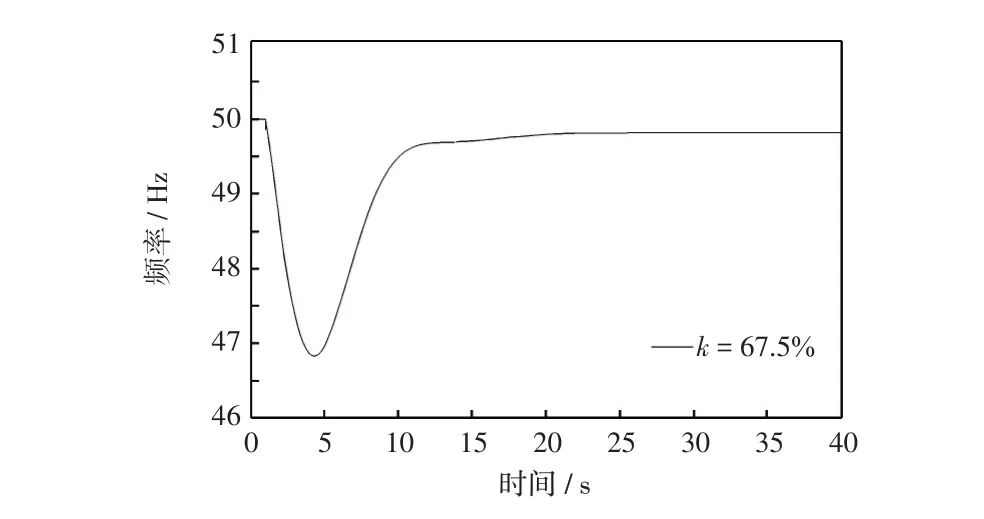
图5 约束条件2 下等容量替换同步机频率响应曲线Fig.5 Frequency response curve of equal capacity replacement synchronous machine under constraint 2

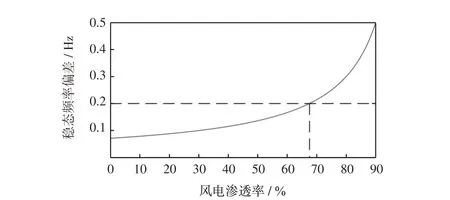
图6 稳态频率偏差与风电渗透率关系Fig.6 Relationship between steady-state frequency deviation and penetration rate of wind power

综合考虑2 个约束条件，可确定不计裕度时等容量替换同步机的风电并网能力kmax为38.3%。

（3）不同惯量水平下的并网能力。为了说明系统不同惯量水平下风电并网对系统暂态频率变化特性产生影响的差异性，本文给出了在满足系统稳定频率约束下，不同的等值惯性时间常数所对应的风电渗透率（或最大替代比例）的临界值，如表1所示。可以看出，3 种情况中稳态频率偏差约束对应的风电最大并网比例相同，最大频率跌落约束是限制风电并网能力的主导因素。

表1 不同惯量水平的风电渗透率的临界值Tab.1 Threshold values of penetration rate of wind power at different inertia levels

4.2 风电并网替换任意比例同步机

对于风电并网替换任意比例同步机的情况，为满足频率稳定约束，剩余功率缺额将依靠改变同步机出力来平衡。

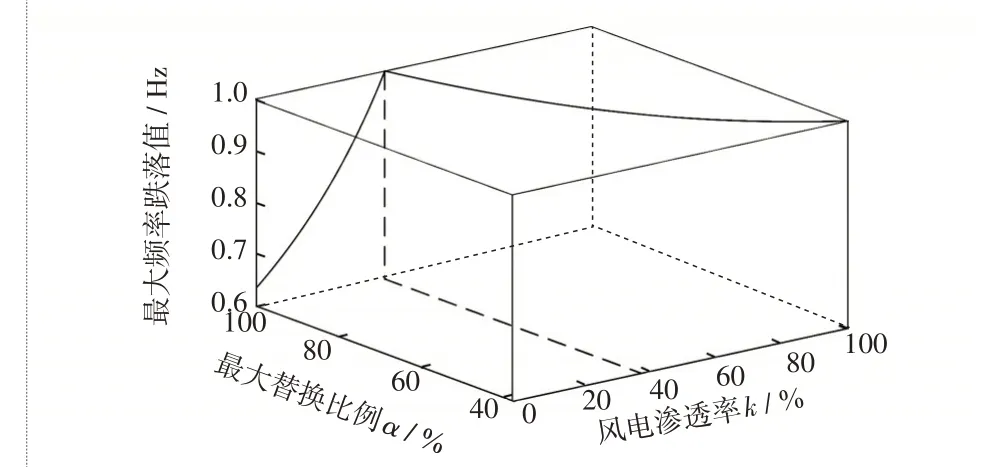
图7 约束条件1 下最大频率跌落值与k、α 的关系Fig.7 Relationship between maximum frequency drop value，k and α under constraint 1

（2）考虑约束条件2。满足该约束条件下稳态频率偏差与风电渗透率、最大替换比例的关系如图8 所示。同样，在达到风电渗透率临界值kcri2=67.5%之前，αmax2始终为1，Δf′∞随渗透率的提高不断增大，在渗透率超过kcri2以后，αmax2将从1 开始减小，以保证Δ不超越0.2 Hz。

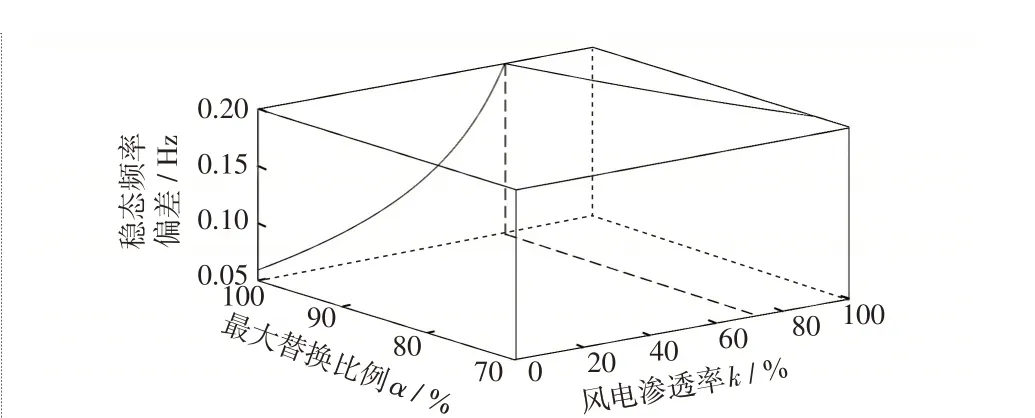
图8 约束条件2 下稳态频率偏差与k、α 的关系Fig.8 Relationship between steady-state frequency deviation，k and α under constraint 2

综合考虑两约束条件即可得到考虑频率特性约束的最佳风电渗透率kmax。

对于高风电渗透电网而言，风电接入比例可能会大于可等容量替换的临界值，利用图8 和图9 所示关系，可以确定出实际风电渗透率所对应的最大替换同步机比例αmax=min{αmax1,αmax2} 。

5 结 论

本文开展了风电并网系统的暂态频率特性和并网能力的评估，结论如下。

（1）理论推导了反映风电并网系统频率响应特性关键指标的时域表达式，给出了风电接入比例和同步机替换比例对系统频率特性的影响关系。

（2）提出了一种考虑频率稳定约束的风电并网能力的确定方法。在满足系统最大频率跌落值和稳态频率偏差的稳定约束要求的条件下，通过寻找到等容量替代同步机的风电临界接入比例，可以确定出与风电接入比例相应的最大替换比例，为高风电渗透率电网并网能力的量化评估提供了途径。

（3）本文所提出的风电并网能力分析方法，有效解决了风电渗透率与同步机替换比例这一矛盾，可为高风电渗透率电网在功率扰动时的同步机投切提供指导，对新能源并网规划设计有一定参考价值。