基于幂次变速趋近律的逆变器环流滑模控制

叶佳卓，邓双喜，周宁博，樊承阳，周朝霞，罗盎捷

（1.湖南大学电气与信息工程学院，长沙 410082；2.长沙轨道交通运营公司，长沙 410082）

随着能源枯竭与电力需求与日俱增，新能源发电技术得到迅速发展。基于新能源的分布式发电系统常采用逆变器多机并联方式，系统容量组合灵活，使远距离和重要负荷供电得到保障，且并网时能减轻主网供电压力，因此逆变器控制技术成为近年来的研究热点。

并联系统中逆变器交流侧因直连而形成通路且线路阻抗较小，当各输出电压矢量存在偏差时易形成环流，产生输出电流畸变、系统损耗增加以及功率分配不均等问题；环流过大时导致逆变器因过载而退出运行。逆变器接入系统或大功率负载投切均会引起输出大幅调整而形成冲击环流，因此采取快速有效的环流抑制策略尤为重要。

针对并联逆变器环流问题，研究学者主要从输出电压控制[1-2]、调节器参数设计[3-5]、输出阻抗[6-7]和参数整定补偿[8-9]等方面抑制削弱环流。文献[2]引进电流反馈量来修正补偿逆变器间电压差使其接近零而达到环流抑制；文献[8]通过递归神经网络控制器并采用对角递归神经网络DRNN（diagonal re⁃anrrent neural networks）参数自整定技术，使准比例谐振QPR（quasi-pportional resonant）参数自整定实现奇偶次谐波抑制从而使输出无静差；文献[9]基于输出电压双傅里叶分析提出载波相位补偿策略来抑制因其不一致产生的环流。

上述方法对系统近似线性化易产生误差，而滑模控制[10-12]作为特殊非线性控制方法，控制精度较高，具有强鲁棒性，对内部参数变化不敏感，抗干扰能力强，且动态响应快。在实际逆变器控制中，文献[11]基于虚拟阻抗滑模控制使系统状态反馈线性化解耦从而消除环流二倍频负序分量；文献[12]基于载波幅度条件的滑模控制方案来控制不平衡三相非刚性径向配电系统的负载总线电压。

本文首先分析系统调整过程中电压幅值、相角变化率与输出功率时间微分的非线性关系式，通过滑模面实现解耦减少线性化误差，针对传统滑模控制中边界层内外趋近速度单一、动态响应慢的问题，设计新型幂次变速趋近律，根据系统当前状态自动调整趋近速度，快速削弱幅值相角波动从而缩小输出差异达到显著环流抑制效果。最后通过仿真验证了该方案抑制环流的快速有效性。

1 并联逆变器环流产生机理分析

假定三相输出电压无磁路耦合且中性点未偏移，则三相逆变器可拆分为3个单相电路，以A相为例，逆变器并联系统环流产生机理如图1所示。

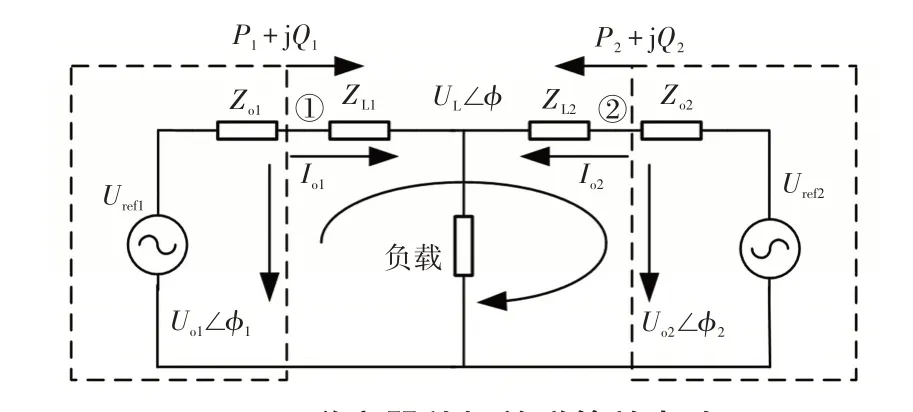
图1 逆变器单相并联等效电路Fig.1 Single-phase parallel equivalent circuit of inverter

图中：Urefn(n=1,2)为逆变器等效参考电压，Zon为逆变器等效输出阻抗，Pn、Qn为逆变器输出有功、无功功率，ZLn为逆变器与公共母线间的线路阻抗，UL为负载电压。当逆变器间电压输出出现差异，可得环流的计算公式为

由式（3）可知，环流与逆变器参考电压、等效输出阻抗及线路阻抗均相关，其中线路阻抗与连接线长短有关而不可控，逆变器等效输出阻抗与频率有关且远大于线路阻抗；参考电压在传统下垂中由控制器结合功率反馈给出。

因此，为抑制产生较大环流，需快速削弱系统调整过程中电压与频率变化，故本文围绕此需求提出基于滑模变结构的环流抑制策略。

2 环流与电压频率功率关联机制

2.1 幅值及频率差异对环流的影响程度分析

基于上述分析知，环流大小与阻抗、参考电压差异等因素有关，而阻抗、电压幅值受频率影响，因此可分析频率与幅值对环流的影响程度。令

2.2 功率波动与电压、频率变化的关联分析

功率/下垂控制作为逆变器并联主要控制方式，通过功率回馈有差调节参考电压与频率使输出达到稳定，且“即插即用”无需互联线。图1等效电路中位置①、②输出复功率为

3 环流控制策略

传统下垂控制策略中下垂系数固定不变，对可变负载调节性能差、计算精度较低，调节过程输出振荡过大导致较大环流，因此为改善动态过程在下垂控制中引入滑模控制并改进趋近律来提高快速性。

3.1 滑模控制模块设计

3.1.1 滑模面设计

3.2 新型幂次变速趋近律

系统状态点趋近滑模面时，可达性条件只保证运动点能到达切换面，而对趋近轨迹与时间没做任何限制。s′表示在当前控制量v下滑模面s趋近变化速度，即有

为判断此趋近律下系统是否存在可达性，取Lyapunov函数为

当状态变量Uref、φ趋于稳定时，由于滤波参数与控制参数的一致性，各逆变器输出电压幅值相位同步。由式（6）分析可知环流得到较好抑制，系统运行稳定性得到保障。

图2 滑模变结构控制框图Fig.2 Control block diagram of sliding-mode variable structure

4 仿真分析

为验证滑模变结构控制下的环流抑制策略可行性，本文在Matlab/Simulink 环境下搭建3 台逆变器并联运行仿真系统。其中2台为实验对象，另一台为模拟实际并网中已有DG单元。每台逆变器设置相同参数，线路阻抗差异明显，并附有不同负载。分别在基于幂次趋近律和新型幂次变速趋近律的2种滑模控制、传统PI下垂控制模型下进行仿真对比研究。仿真参数如表1所示。

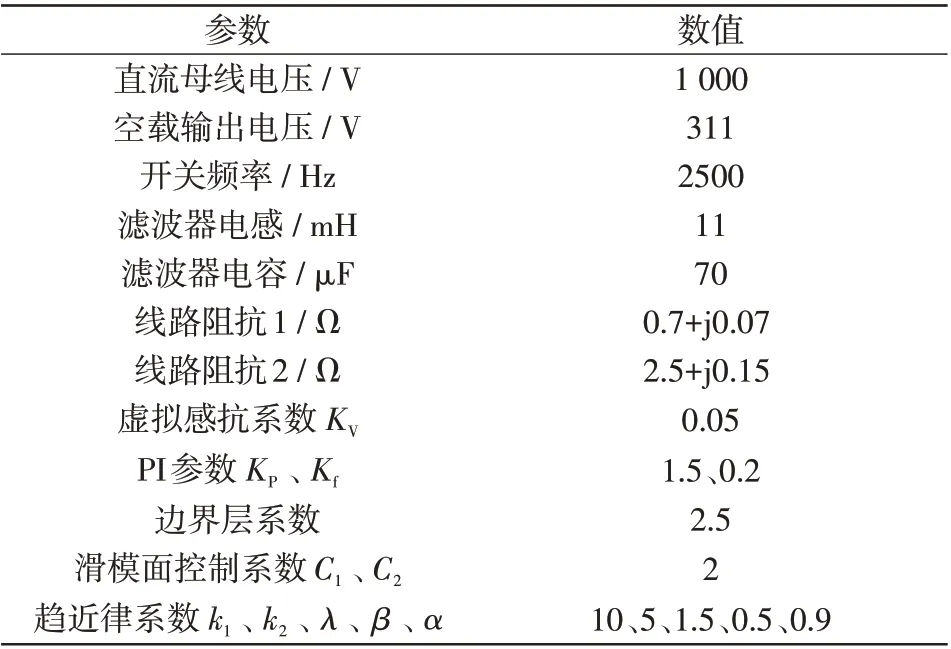
表1 系统仿真参数Tab.1 Simulation parameters of system

4.1 逆变器并入系统仿真分析

系统仿步长为1 μs。图3为传统下垂控制模式与加入滑模模块系统接入时输出电压差、频率差异以及环流变化情况。

图3（a）中，传统下垂控制中输出电压差异波动剧烈，范围在-50～100 V 之间；且因下垂系数为定值，动态调整用时为0.04 s 左右，是加入滑模控制方式的1.5 倍。而新型趋近律因变速项的存在，相较于幂次趋近律，在调整前半段能迅速降低输出差异，在0～0.02 s 之间其电压差值为幂次趋近律的2/3；调整后半段即进入边界层时新型趋近律调整平滑，抖振幅度也明显低于幂次趋近律；整体调节时间节省15%左右。频率差值变化如图3（b）所示，新型趋近律下调节幅度低，且系统稳定更快。

逆变器并网稳定前因各电压存在差异而产生环流。图3（c）中传统下垂的初始环流波动大且最高达到10 A易烧毁功率开关器件，稳定时环流周期性波动但幅值较大。新型趋近律环流在0.035 s 步入稳定，相较于幂次趋近律的0.050 s，缩短1/3且幅值低，与前文分析相符合。新型趋近律系统响应更快，初始动态环流抑制性能优越。

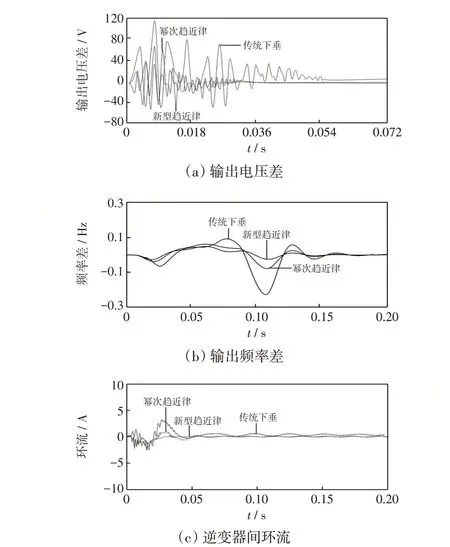
图3 并入系统时观察量变化曲线Fig.3 Observation curve when connected to the system

4.2 负载投切干扰实验仿真分析

为探究滑模控制系统抗干扰能力，在系统平稳运行至0.3 s时投入恒功率负载（有功功率9 000 W，无功功率1 000 var），观察系统输出电压幅值差和环流情况。负载干扰实验分析如图4所示。

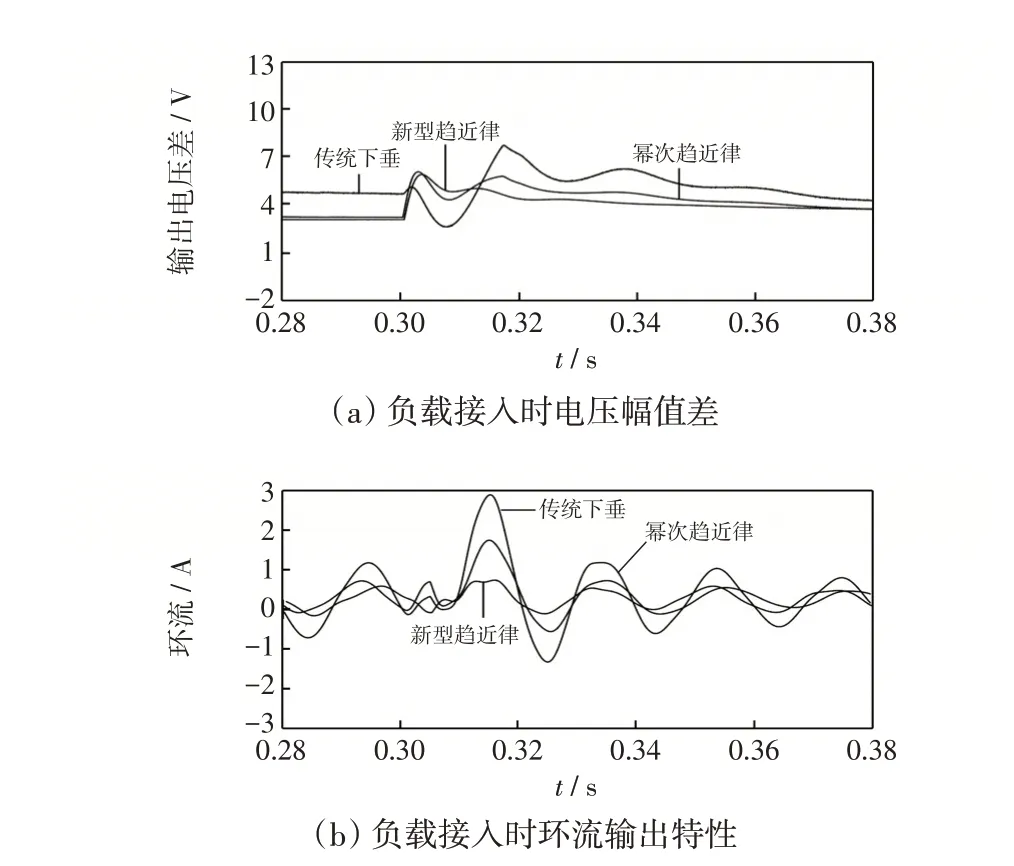
图4 负载干扰实验分析Fig.4 Analysis of load disturbance experiment

由图4（a）、（b）中可见，系统稳定时因线路阻抗差异输出间仍存在微小差异。0.3 s时负载接入，传统下垂控制在调整过程中电压差与环流均较大；而滑模控制下各输出电压差与环流波动降低50%，同时新型趋近律在受到干扰后相较于幂次趋近律提前步入新稳态，超调量全程降低。

4.3 新型趋近律参数调整仿真分析

新型趋近律中变加速项主要受参数k1和λ影响，为探究上述参数对环流抑制效果与影响程度而进行仿真分析，结果如图5所示。

图5 参数调整仿真分析Fig.5 Simulation analysis of parameter adjustment

由图5（a）可知，当其余参数一致时k1越小，则干扰情况环流调整波动越大，但所需调整时间与波动趋势并未明显改变，且稳态精度基本一致。在图5（b）中，系数λ过大或过小在初始调整时波动均较大，但0.32～0.38 s后续调整期间环流波动幅度越小且更快恢复到稳态。

综合分析，幂次变加速项中参数k1只影响系统初始超调量，但对快速性无明显改善；而参数λ对系统超调量呈抛物线下降趋势，但系统快速性能随参数增大而提高，响应时间呈负相关。

5 结 语

本文针对系统调整过程时所产生的过大动态环流，提出一种新型趋近律下的滑模控制策略。该策略基于滑模控制并基于系统状态点自动调整输出变化速率与幅值，趋近律中所设计幂次变加速系数能有效降低系统输出变化幅度，调整平滑且响应更快，系统鲁棒性得到有效提升。仿真结果验证本文所提控制策略环流抑制快速有效。