GeoGebra在验证猜想中的应用
俞 翔 李 更
(宁波市奉化区江口中学 浙江 宁波 315504)
物理教师应用GeoGebra软件辅助教学的能力日渐娴熟,由《物理通报》近几年发表的文献可见微知萌,在2017至2019年共有文献4篇,2020年有文献6篇,2021年截至4月已有4篇.纵观这些文献,GeoGebra多应用于物理场景的建立和疑难问题可视化的研究,如陈林老师借助3D绘图实现对电场电势的三维建构,艾亮老师利用微积分思想研究v-t图像中的面积.现就一改编题,借助GeoGebra应用于对未知规律的探寻和验证.
1 等时圆模型的应用
【例题】如图1所示,ad,bd,cd是竖直面内3根固定的光滑细杆,a,b,c,d位于同一圆周上.每根杆上都套着一个小滑环(图中未画出),3个滑环分别从a,b,c处释放(初速为零),用t1,t2,t3依次表示滑环到d所用时间,则( )

图1 例题图
A.t1
C.t3>t1>t2D.t1=t2=t3
解析:鉴于d点并非圆周的最高点和最低点,要应用等时圆模型,需构建等时圆.以d点为圆周的最低点,过b点做圆,如图2所示.此圆与ad和cd轨道相交于a′和c′,由等时圆模型的规律可知,若小滑环自a′,b和c′由静止开始下滑至d点所用的时间相等.从而可见,自ad下滑的时间t1小于自bd下滑的时间t2.同理,自bd下滑的时间t2小于自cd下滑的时间t3.所以,选项A正确.

图2 借助等时圆模型巧解例题
2 等时圆模型的拓展
由于题目中并未明确表明d点的位置,不妨将d点向下移动,如图3所示.

图3 研究普适规律
移动d点并不会变更题目本意,即应有不变的结果t1 图4 滑轨处于圆心侧上方 得 对于确定的d点而言,β为定值,所以当α角度逐渐减小时,t值增大. 如果ad弦低于圆心O,如图5所示,则有 当α角度逐渐减大时,t值仍增大. 图5 滑轨处于圆心侧下方 从而可见,只要落点d相同,开始下滑的位置越高,所用时间越小,即始终有t1 “圆时间规律”的结论t1 细细推敲等时圆模型的规律和“圆时间规律”均没有问题.猜想在d点下移的过程中,尽管下滑的时间会变化,且各轨道所用时间t1,t2,t3不等,但与之同时t1,t2,t3之间的差值在逐渐减小. 为验证猜想,采用GeoGebra制作动画研究时间差.做一个半径为5的圆,并按题设在圆周上取a,b,d点建立下滑轨道,设置顶角γ用以记录d点在圆周上位置的变化,d点越接近于圆周最低点,角度γ越小.借助Length指令获取两个轨道长度,借助角度工具获取斜面倾角.利用匀变速运动公式计算下滑时间,并求时间差,如图6和表1所示. Δt=t2-t1=1.86 s-1.56 s=0.3 s 图6 圆和轨道 表1 通过软件获取研究所需数据 在d点代数区设置其“增量”为5,“速度”为3的情况下启动动画.观察d点下移过程中,不同轨道下滑的时间差,并借助“记录到表格”功能以获得数据列表.从数据清晰可见,伴随着d点的下移,γ角趋向于零,t1与t2的数值逐渐逼近,即Δt=t2-t1趋向于零. 将动点d的“速度”降低到0.1,以获取更多的数据,并在GeoGebra中以Δt为横坐标,γ角(弧度值)为纵坐标创建点阵,如图7所示.由图7可见,在d点下移到最低点的过程中,通过不同轨道下滑的时间差趋向于零. 通过研究可知,若在圆周一侧取一位置略低的d点,作为斜面底边的端点,从圆周另一侧选取一些点作为光滑斜面的顶点,让物体自各顶点下滑,下滑的时间和各顶点到d之间的高度差有关,高度差越大,时间越小.其成立的条件是d点不能是圆周的最低点. 图7 γ-Δt点阵 该测试题改编自2004年高考全国理综卷Ⅰ,原题中“d点为最低点”,正确选项是D.借助于GeoGebra的探究,也发现改编题默认d点为一侧点的做法略有不当,在试题中增加一条“d点非最低点”的条件,让试题更为严谨.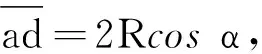


3 问题的产生 猜想与论证




