二维大地电磁主轴各向异性理论模型反演

张双全，李桐林

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

大地电磁法(maganetotelluric method，MT)利用天然存在的大地电磁场，能反映出地壳和上地幔范围内的地下电性结构，具有其他勘探方法无法比拟的优势。电性各向异性是指电导率随方位变化的现象。Wannamaker[1]详细论述了电性各向异性在地电模型和地球动力学解释中的重要作用，还说明了各向异性介质普遍存在于地球内部。但在实际应用的大地电磁数据采集和分析解释流程中，通常直接简单地将地下介质设定为各向同性情况而忽略电性各向异性现象，这样很容易漏掉甚至得到不真实的地质信息[2]。

20世纪60年代末对电导率各向异性的理论研究逐渐发展起来。Reddy et al.[3]首次对二维电性各向异性偏微分方程用有限元法做了数值计算，对后世的理论研究留下了尤为深远的影响。进入20世纪90年代在计算机技术的辅助下，电磁数值模拟技术飞速发展，电各向异性研究也取得重大突破[4]，有限元法和有限差分法被广泛用于二维大地电磁各向异性的正演模拟中[5]。其中Pek J et al.[6]

在Reddy et al.[3]基础上，将前人Haak[7]，Brewitt--

中国关于电性各向异性的研究虽然晚于国外，但也取得了许多成果。Li[11]公布了二维各向异性电磁法有限元算法，并在后来与Pek J用自适应的网格剖分法将算法做了改进[12]，是二维各向异性有限元电磁模拟中影响较为重大的研究成果。杨长福等[13]在Pek J的理论基础上，将电导率简化为对称各向异性介质，反演了甘肃天祝永登一带的大地电磁资料数据并取得了不错的效果。胡祥云等[14]将Pek J的研究方法应用到新疆某地的大地电磁资料处理中，做了二维正演拟合解释，验证了算法的实用性和理论的正确性。由于各向异性反演较为复杂，单纯利用大地电磁各向异性的应用案例较少，笔者编写了Matlab计算程序，并反演计算了多个二维模型，为更广泛地应用大地电磁各向异性提供了理论依据。本研究存在一定局限性，只是考虑了主轴各向异性的情况，忽视了各主轴与构造的夹角，而且反演的是较为简单的理论模型，没有研究大地电磁实测数据资料。介于目前国际上还未出现成熟的、可同时反演3个主轴电阻率和旋转角的算法，且各向异性识别方面的研究也不够完善，导致电性各向异性在实际生产资料处理中应用不多，因此不考虑旋转角，只计算主轴电阻率，不失为一个较好的突破口，也有一定的应用价值，能为今后处理解释复杂的大地电磁资料的电性各向异性现象提供思路和方法。

1 方法理论

1.1 正演算法

本文使用的二维大地电磁各向异性有限差分正演理论来自Pek et al.[6]的研究方法，已有许多学者验证了其正确性。

对任意各向异性异常体，假设在笛卡尔坐标系中，其走向平行于x轴，y轴垂直于x轴，z轴垂直于xy平面且向下为正向。地表水平且对应z=0，地表上空是空气层，来自高空的平面波垂直地表向下传播，有：

它可分解为3个主轴方向的电导率和一个由3个Euler’s空间旋转角αL、αD和αS组成的旋转矩阵。将其带入麦克斯韦方程组，忽略位移电流后，可得到以下一组关于电场分量Ex和磁场水平分量Hx的二阶偏微分方程(严格来说在各向异性情况下，电场和磁场分量耦合，已不存在“纯粹”的TE模式与TM模式，不过为表述方便，下文依然将电场沿走向的E极化模式称作“TE模式”，将磁场沿走向的H极化模式称作“TM模式”)：

TE模式：

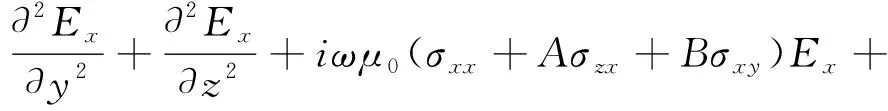
(1)

TM模式：

(2)

从以上两个公式可见，任意各向异性情况下，

TE模式：

(3)

TM模式：

(4)

从公式(3)和(4)可以看出，电场分量Ex和磁场分量Hx已成功解耦，为单独反演电场分量和磁场分量提供了提论依据。TE模式只反映σxx且在形式上公式(3)与二维各向同性介质相同，只是在物理意义上公式(3)中反映的是沿走向方向的电导率值，这意味着此时二维各向同性介质的数值模拟方法甚至程序可直接利用，还可推广至反演[13]。二维大地电磁各向同性介质的正反演已非常成熟，因此本文不再研究二维各向异性TE模式的计算。相比各向同性介质，二维各向异性介质情况下的TM模式就复杂一些，公式(4)可以看出TM模式依然同时与σyy和σzz两个电导率值相关，且σyy≠σzz，各向同性介质下的计算程序无法直接使用。

相应地， TE模式下每个节点列方程时的10个系数只剩下和电场分量有关的5个，TM模式下的14个系数也只剩下和磁场分量有关的5个。

1.2 反演算法

针对反演问题已有多种数值优化技术，如Occam、非线性共轭梯度、高斯牛顿、拟牛顿法和最小二乘法等[4]。本文采用最小二乘法，使用基于先验模型的最光滑模型约束。

反演的总目标函数可以表示为：

Pα(m)=‖[dobs-F(m)]‖2+α‖Wm(m-mref)‖2

(5)

式中：Pα(m)表示总目标函数；α是正则化因子；F表示正演响应，Wm是光滑度矩阵，或称模型权系数矩阵；mref是先验模型。

Pα(mk+1)=‖[dobs-dk-JkΔm‖2+α‖Wm(mk-mref)‖2

(6)

上述函数对Δm求导并令它等于0，写成迭代形式为:

[dobs-dk+Jmk-Jmref]

(7)

J是雅可比矩阵，也称灵敏度矩阵，代表每个数据对模型参数的偏微分。雅可比矩阵可用差分或伴随阵等方法计算得到。对公式(7)进行反演迭代，将计算得到的优化模型改变量不断更新，重复计算目标函数，直至目标函数减小到符合精度要求即可。

2 二维主轴各向异性模型计算与分析

模型1

图1 理论模型1Fig.1 Theoretical model 1

计算时将模型剖分为72×24的剖分单元(垂向24个剖分单元，不用包含空气层)，测点数为72个(即地表的网格节点处)，采用25个周期点(0.01，0.03，0.05，0.07，0.1，0.3，0.5，0.7，1，3，5，7，10，30，50，70，100，300，500，700，1 000，1 300，1 500，1 700，2 000，单位s)。反演初始模型设置为与介质1完全相同的各向同性均匀半空间。

从反演结果来看(图2)，y轴方向上成功反演出了异常体的水平位置和深度。在实际异常区域内值大约为160 Ω·m，略小于真实值200 Ω·m，这是因为MT平面波的性质，即极化电场和磁场在水平方向衰减，且在高阻中衰减缓慢。z轴方向上反演的ρzz与真实模型不一致，而是与背景空间接近。

(a)y轴方向电阻率反演结果；(b)z轴方向电阻率反演结果。图2 理论模型1的反演结果Fig.2 Inversion results for theoretical model 1

模型2

从反演结果来看(图3)，与图2类似，y轴方向上的效果好于z轴。y轴方向上除了较好地反演出了异常体的位置，还成功反演出了异常体的真实值为20 Ω·m，而z轴方向上则没有取得较好的效果。

(a)y轴方向电阻率反演结果；(b)z轴方向电阻率反演结果。图3 理论模型2的反演结果Fig.3 Inversion results for theoretical model 2

模型3

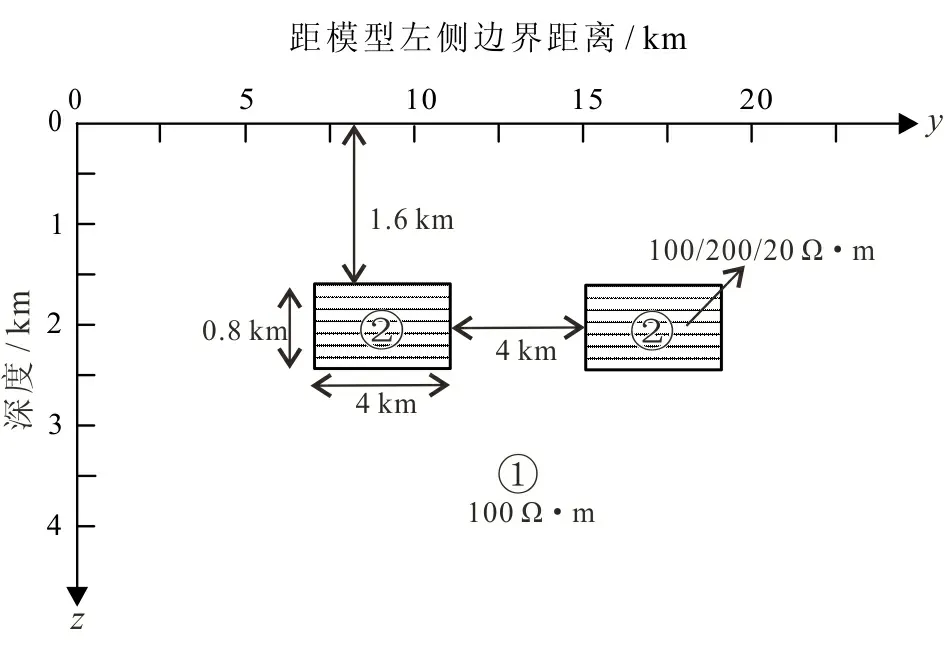
图4 理论模型3Fig.4 Theoretical model 3

计算时将模型剖分为52×24的剖分单元(垂向24个剖分单元，不用包含空气层)，测点数为52个(即地表的网格节点处)，采用25个周期点(0.01，0.03，0.05，0.07，0.1，0.3，0.5，0.7，1，3，5，7，10，30，50，70，100，300，500，700，1 000，1 300，1 500，1 700，2 000，单位s)。反演初始模型设置为与介质1完全相同的各向同性均匀半空间。

从反演结果来看(图5)，y轴方向上成功反演出了两个异常体的水平位置和深度。ρyy在实际异常区域内值大约为150 Ω·m，略小于真实值200 Ω·m。z轴方向上反演的ρzz与真实模型不一致，而是与背景空间接近。

(a)y轴方向电阻率反演结果；(b)z轴方向电阻率反演结果。图5 理论模型3的反演结果Fig.5 Inversion results for theoretical model 3

模型4

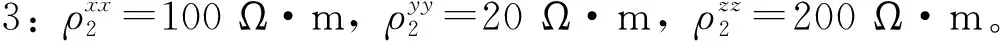
从反演结果来看(图6)，与模型3类似，y轴方向上成功反演出了两个异常体的水平位置和深度；z轴方向上反演的ρzz与真实模型不一致，而是与背景空间接近。右侧高阻模型的ρyy在实际异常区域内的值约为140 Ω·m，小于真实值200 Ω·m，且小于模型3中的150 Ω·m，说明右侧的高阻体受到了左侧低阻体的影响；左侧低阻模型的ρyy在实际异常区域内的值约为20 Ω·m，与真实值相等。

(a)y轴方向电阻率反演结果；(b)z轴方向电阻率反演结果。图6 理论模型4的反演结果Fig.6 Inversion results for theoretical model 4

综合以上4个反演结果，可见MT响应对低阻异常更为敏感。相较高阻，反演能更有效地恢复低阻电阻率；相较纵向，水平方向异常体的范围圈定要更准确些。同时这4个模型还说明了在二维各向异性反演中恢复ρzz几乎是不可能实现的，这是由于其非固有唯一性导致的。Yin[15]证明了主轴各向异性情况下ρzz不可能反演恢复；Chen[16]在二维各向异性反演中得到了相同的结论。

3 结论

本文编程实现了二维大地电磁各向异性“TM”模式下理论模型的最小二乘反演。反演计算了单个异常体模型和多个异常体模型，在y轴方向上均得到了较好的反演结果：位置圈定上，异常体的范围与理论模型非常接近，水平方向上的范围极为准确，纵向上稍差一些；电阻率上，高阻体会受到低阻体的影响，低阻的电阻率恢复相较高阻更加准确。反演结果同时验证了前人关于z轴方向上的电阻率由于ρzz不敏感，无法成功恢复的研究结论。

致谢感谢捷克科学院地球物理研究所Josef Pek教授对正演算法的提供。