重力场欧拉反褶积最优化滑动窗口选择

杨博，曹书锦,，毛雅静，周勇，朱自强，陈新跃

1.湖南科技大学 页岩气资源利用湖南重点实验室，湖南 湘潭 411201；2.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411201；3.中南大学 地球科学与信息物理学院，长沙 410083；4.湖南文理学院 资源环境与旅游学院，湖南 常德 415000

0 引言

欧拉反褶积法能使用少量先验信息且不需要准确的解释模型，即可快速准确地圈定异常源的基本轮廓或标识异常源中心，特别适合大尺度重磁位场数据的快速解释。欧拉反褶积法一般通过一定大小的滑动窗口在整个勘探区域移动，根据人工经验或枚举构造指数，在滑动窗口内基于欧拉齐次方程构建线性方程组[1--7]。该线性方程组由人为设定大小的滑动窗口内的观测数据构建，其条件数极大，这导致欧拉反褶积易于受到观测数据噪声、异常源形态及其空间位置和滑动窗口尺寸等因素的影响。

在实际地质情况中，地质构造一般为多个不同形态异常源的组合，传统欧拉反褶积解释工作流程中仅使用单一构造指数易于导致欧拉解发散，而通过枚举构造指数易于导致欧拉解集过于庞大[8--14]，单一过滤标准又将忽视其他异常源[1]。张季生等[15]针对欧拉反褶积方法易受高频干扰的问题，提出低阶的欧拉反褶积与解析信号相结合的位场反演方法，将高频噪声的干扰减少到可以控制的水平[16]。此外，将重力梯度张量解析信号引入欧拉反褶积，或将重力梯度张量数据进行联合欧拉三维反演，以提高欧拉反褶积解的收敛性[17--18]。

对于欧拉反褶积在具体实施过程中最优化窗口选择的问题，周文月探索了小窗口多数据对欧拉反褶积方法的影响，在一定程度上解决了采用大窗口时解的平滑问题，以及不同场源混叠相互干扰引起的解的不精确问题[19]。Krahenbuhl et al.[20]指出过小的滑动窗口难以获得地下异常源信息，而过大的滑动窗口易于引入相邻异常源的干扰，但没有给出如何选择最优滑动窗口大小的策略。研究最优滑动窗口大小确定方法，可以有效地捕捉地下异常源信息、减少欧拉反褶积解集大小和提高工作效率[1, 21--22]。

为此，针对超定的欧拉齐次方程组易于受到多种因素的干扰，笔者引入截断误差对欧拉反褶积解的优良性进行评价，并引入模糊聚类对欧拉反褶积解集进行划分[3]，在此基础上，当异常源尺寸一定时，以不同深度的异常源、不同尺寸的滑动窗口和欧拉解集中优解的比例等三者为研究对象，分析滑动窗口尺寸和异常源尺寸间的比例关系，以此选择最优化窗口。最后，数值算例进一步表明了方法的有效性。

1 欧拉反褶积

重力场欧拉齐次方程可以写为[23]：

fx(x-x0)+fy(y-y0)+fz(z-z0)=Nf(x-x0,y-y0,z-z0)+NB

(1)

式中：f为位于点(x，y，z)的异常源在观测点(x0，y0，z0)处产生的异常响应；fx、fy和fz为f沿x、y和z轴向的梯度，可通过离散傅立叶变换或离散余弦变换获得；N为异常幅值随场源深度衰减变化“陡缓”的量度，即构造指数；B为正常场存在的偏差，主要是为消除区域背景场的影响而引入的一个代表背景场的参数。在传统欧拉反褶积法中，一般通过人工经验选择或枚举构造指数N求解式(1)，但单一构造指数N易于导致欧拉解发散或无解；而在一定范围内，如0～3，以某一步长枚举构造指数N易使欧拉解解集过于庞大，导致解释工作量剧增。为此，将构造指数N作为待求参数，将式(1)重写为：

xfx+yfy+zfz+Nf=x0fx+y0fy+z0fz

(2)

由于B数量级很小，故此，在式(2)中已将B略去。在欧拉反褶积中，一般利用长宽均为wx的滑动窗口在勘探区内移动。对于每个滑动窗口而言，以滑动窗口内的n=wx×wx个观测值根据式(2)构建线性方程组，并求解该方程组以获得欧拉解(x，y，z，N)。

将构造指数N当作未知数求解可在一定程度上避免欧拉解发散，但式(2)本质上仍然是求解超定的欧拉齐次方程，因而欧拉解仍然存在发散的趋势。为此，以截断奇异值分解法得到的误差来估计欧拉解的优良性，以聚类分析来划分欧拉解解集，并评价欧拉解解集中各簇的优良性。在此基础上，分析滑动窗口的尺寸与地下异常源尺寸的关系，研究最优滑动窗口大小选择标准，以满足在反演地下不同尺寸异常源的同时，减少相邻干扰信息的侵入，控制欧拉解集的大小，降低欧拉反演的后续处理工作量。

2 截断误差估计

将滑动窗口内n个观测值f代入到式(2)所得到的线性方程组写为矩阵的形式：

Gm=b

(3)

式中：G为[fxfyfzf]；b为x0fx+y0fy+z0fz构成的向量；m=[x，y，z，N]T为欧拉解。

式(3)为超定方程组，因而在勘探区内移动滑动窗口时，欧拉反褶积可能因为式(3)条件数过大而导致无解(即解为非数的情况)，或有解但不为正确解/优解(如欧拉解的空间位置不在勘探区内、构造指数不在合理范围内等)。为此，这里采用截断奇异值分解法对式(3)的误差进行估计，并在此基础上，构建一个估计函数εr以过滤欧拉解集中的缪解：

(4)

式中：ε为截断奇异值分解法对式(3)的误差估计值。

3 模糊聚类原理

为判定不同大小的滑动窗口反演地下异常源的能力，特引入聚类分析方法将欧拉解集按相似性分类，以标示地下多个不同的异常源。在多种聚类分析方法中，基于划分的模糊聚类分析不需要训练样本，仅通过无监督学习达到自动分类的目的，最终能够获得比较客观地反映地质构造的簇。模糊聚类不但能从原始数据中提取特征，而且能在提取特征之后，进一步提供最近邻原型分类器和提取空间划分特性等。为把p个向量xi(i=1，2，…，p)分类成c个簇，并使得目标函数最小，求得簇的分类信息和簇的中心，以模糊聚类算法构建如下目标函数：

(5)

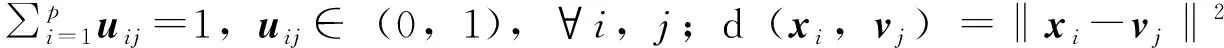
(6)

(7)

由模糊聚类得到的欧拉解簇的聚集程度可由下式计算得到：

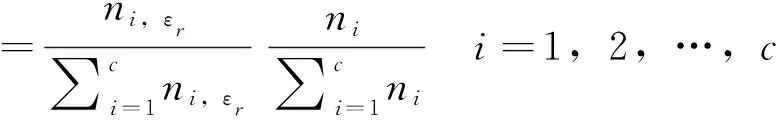
(8)

式中：ni为第i个欧拉解簇中元素的个数；ni,εr为第i个欧拉解簇中优解的个数。

4 模型试验

4.1 算法验证

为验证本文欧拉反褶积算法和基于截断奇异值分解法设计的估计函数的正确性，特基于有正演解析解，且构造指数易于确定的立方体模型，构建如下地球物理模型I：在地下均匀半空间内，存在一个大小为500 m×500 m×500 m、顶板埋深为200 m、底板埋深为700 m且剩余密度为0.3 g/cm3的异常体。以大小50 m×50 m×50 m的网格离散该地球物理模型，网格沿着笛卡尔坐标系三轴向的剖分数nx、ny和nz分别为32、32和16；观测点间距为50 m×50 m，观测点个数为nx×ny=32×32=1 024，即勘探区尺寸为1 550 m×1 550 m，观测点高度为地面上25 m。

首先，通过解析解计算立方体异常源的重力异常响应f，并在f中添加3%的高斯噪声作为观测数据，继而利用快速傅立叶变换计算得到fx、fy和fz。在此基础上，应用式(3)计算异常源的空间位置及其构造指数，利用聚类分析对欧拉解集进行分类，并采用估计函数εr对欧拉解的优良性进行判定。

图1为孤立异常源的欧拉解分布示意图，滑动窗口尺寸wx为5。从图中可以看出构造指数趋近于2(立方体异常源构造指数的理论值为2)的欧拉解聚集于异常源中心，这表明了本文算法的正确性。

图1 孤立异常源欧拉解分布示意图Fig.1 Scatter plot of Euler solutions for a single anomalous sources

进一步，以εr>0.25为标准过滤孤立异常源的欧拉解，其分布如图2所示。通过与图1进行对比，可以发现基于εr过滤后的欧拉解能有效的标示异常源的空间位置，而且尽可能的保留了一些构造指数偏离理论值的欧拉解，如N≤1.5的欧拉解。这表明本研究提出的估计函数的正确性。

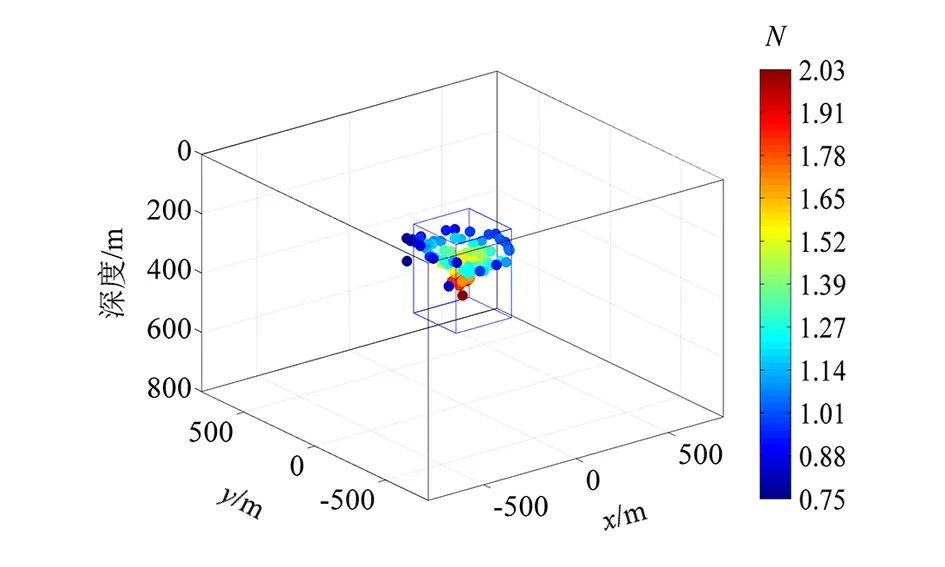
图2 孤立异常源的欧拉解以εr>0.25为标准过滤后的分布示意图Fig.2 Scatter plot of Euler solutions for a single anomalous sources filtered by εr>0.25

4.2 不同尺寸滑动窗口提取不同深度孤立异常源的能力分析

为研究不同尺寸滑动窗口提取不同深度孤立异常源的能力，在其他参数与地球物理模型I保持一致的前提下，将地球物理模型I以步长Δz沿Z轴向下移动从而生成一系列不同深度的孤立异常源模型II，其中勘探区尺寸与4.1小节中一致。

解率为欧拉解集中不为非数的解与欧拉解个数的百分比。在欧拉反褶积中，滑动窗口wx最小为3。在勘探区域内，滑动窗口沿着x和y轴移动的最大步数分别为nx-wx和ny-wx，滑动窗口移动次数最大为(nx-wx)×(ny-wx)，且欧拉解集中解的个数小于或等于这一数字。因而，对于固定大小的勘探区域，随着滑动窗口尺寸不断增大，解的数目在不断的减少。

由图3可见，当滑动窗口较小时，即滑动窗口尺寸小于勘探区域的1/4时，浅部异常源对应的有解率比深部的要大；当滑动窗口尺寸约为勘探区域的1/4～1/2时，深部异常源对应的有解率比浅部的要大；而当滑动窗口尺寸大于勘探区域尺寸1/2时，不同深度的异常源对应的有解率几乎一致。

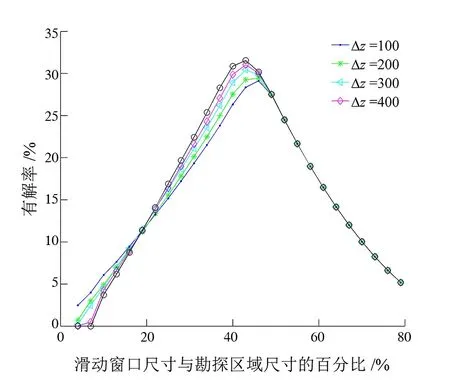
图3 不同尺寸滑动窗口下不同深度孤立异常源的有解率曲线Fig.3 Different moving window sizes for Euler solution rate of isolated anomalous sources with various offset Δz

优解率为欧拉解集中优解(排除空间位置不在勘探区内、构造指数不在合理范围内的欧拉解)与欧拉解集中不为非数的解的个数的百分比。图4为利用估计函数εr对不同深度孤立异常源的欧拉解进行过滤后的优解率曲线。当滑动窗口很小时，浅部异常源对应的欧拉优解率占优；随着滑动窗口的增大，这一关系仍然得以保持；当滑动窗口尺寸大于勘探区域的1/2时，不同深度异常源对应的优解率趋于一致。

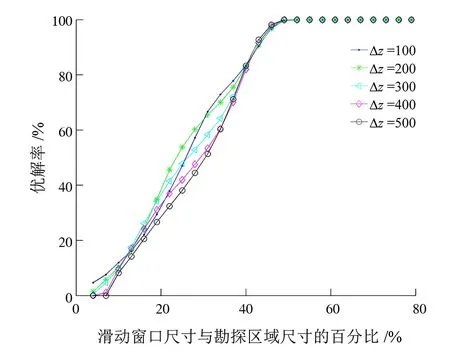
图4 不同尺寸滑动窗口下不同深度孤立异常源的优解率曲线(3%高斯噪声)Fig.4 Different moving window sizes for optimal Euler solution rate of isolated anomalous sources with various offset Δz, survey data contaminated with 3% Gaussian noise

在图4中试验的基础上，进一步在观测数据中添加7%的高斯噪声，以对比不同噪声情况下，不同尺寸滑动窗口提取不同深度孤立异常源的能力(图 5)。当滑动窗口很小时，几乎难于提取深部异常源的有用信息；随着滑动窗口的不断增大，欧拉反褶积优解率曲线的斜率先增大后放缓，且这种趋势在深部异常上更为明显。相比于图4，随着孤立异常源的观测数据中噪声的增加，将导致基于小滑动窗口的欧拉反褶积难于提取到有用信息。

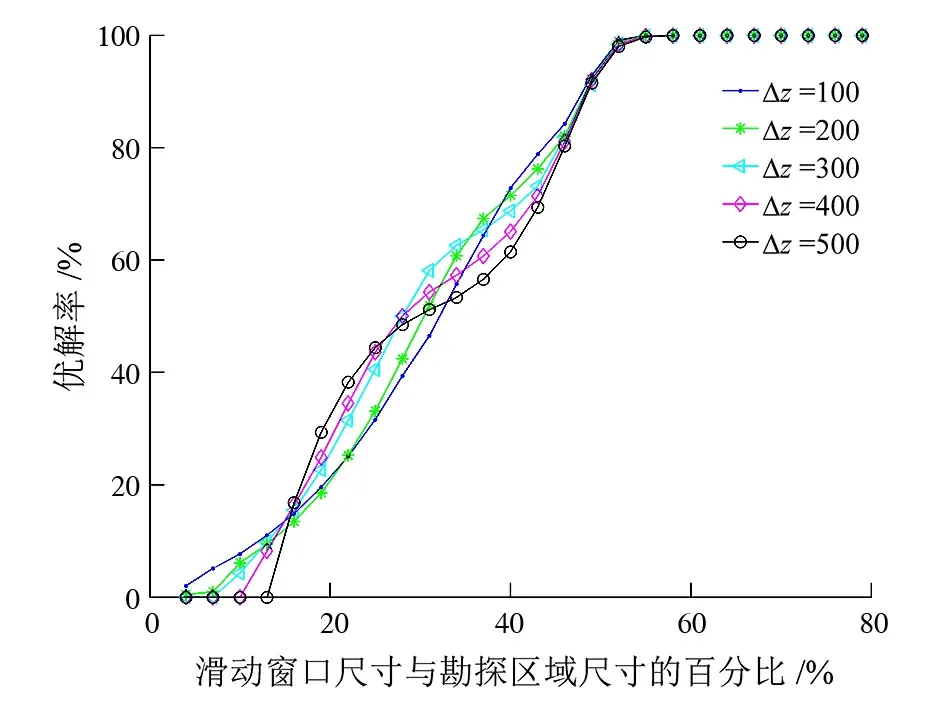
图5 不同尺寸滑动窗口下不同深度孤立异常源的优解率曲线(7%高斯噪声)Fig.5 Different moving window sizes for optimal Euler solution rate of isolated anomalous sources with various offset Δz, survey data contaminated with 7% Gaussian noise

4.3 不同尺寸滑动窗口提取不同深度组合异常源的能力分析

在上述研究的基础上，进一步研究不同尺寸滑动窗口提取不同深度组合异常源的能力，特设置如下地球物理模型III：由两个剩余密度均为0.3 g/cm3且大小均为500 m×500 m×500 m的异常源组成，两者质心分别为(0 m，-1 500 m，500 m)与(0 m，1 500 m，700 m)。以大小50 m×50 m×50 m的物性网格离散该地球物理模型，网格沿着笛卡尔坐标系三轴向的剖分数nx、ny和nz分别为101、101和50；观测点间距为50 m×50 m，观测点个数为nx×ny=101×101=10 201，即勘探区尺寸为5 000 m×5 000 m。观测点高度为地面上25 m。以步长Δz沿Z轴向下移动从而生成一系列的地球物理模型IV。

本小节中观测数据的计算与4.1小节中相同，通过式(3)获得组合异常源的欧拉解集后，利用模糊聚类对欧拉解集进行分簇，通过式(8)计算欧拉解中的优解率来判定最优的滑动窗口大小。这里优解率定义为模糊聚类的簇中欧拉优解的个数与欧拉解的个数的百分比。

图6为组合异常源中深部异常源在不同尺寸滑动窗口下的优解率曲线，总的趋势为随着异常源深度的增加，优解率在不断地降低。对于深部异常源而言，随着滑动窗口的增大，优解率先增大后逐渐减小；当滑动窗口尺寸约为异常源尺寸的3倍时优解率最大，且当滑动窗口尺寸大于勘探区尺寸的1/2时，将导致欧拉反褶积难于提取到有用信息。

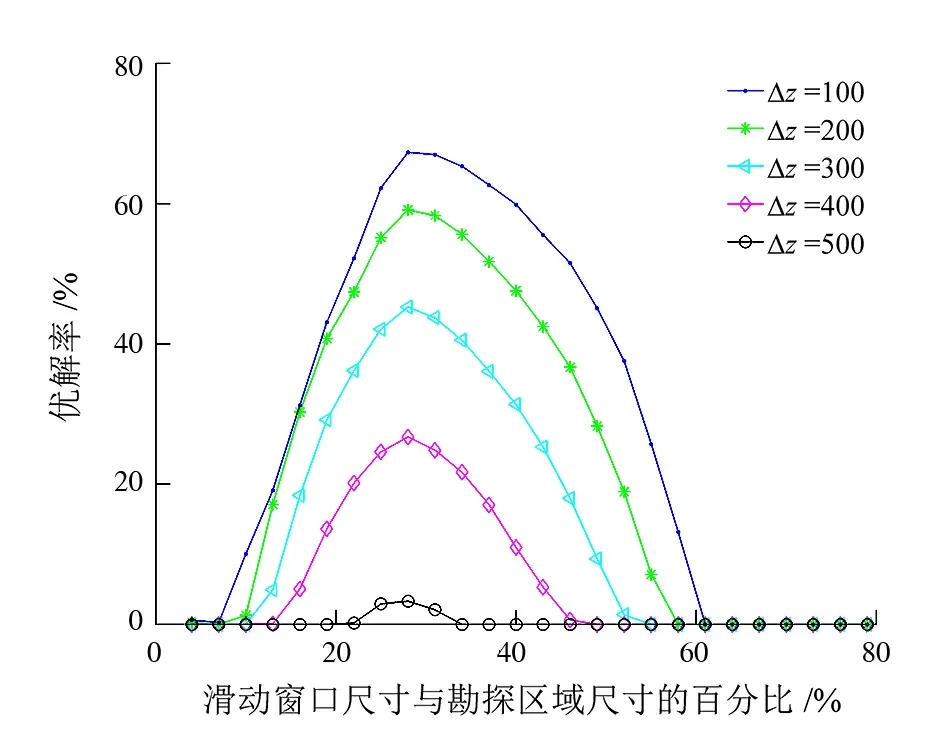
图6 深部异常源不同尺寸滑动窗口下的优解率曲线Fig.6 Different moving window sizes for optimal Euler solution rate of deep anomalous sources with various offset Δz

图7为组合异常源中浅部异常源在不同尺寸滑动窗口下的优解率曲线，总的趋势与图 6类似，随着异常源深度的增加，优解率在不断地降低。当Δz=100和Δz=200时，随着滑动窗口的增大，优解率先增大后变缓，并因受到深部异常源的干扰，出现一定的波动。当Δz=300、Δz=400和Δz=500时，随着滑动窗口的增大，优解率先增大后逐渐减小；当滑动窗口尺寸约为异常源尺寸的3倍时获得最佳的优解率。与图6相比，由于深部异常属于弱异常源，其位场总场效应相对较小，因而滑动窗口尺寸过大，易于导致欧拉反褶积难以提取有效异常。与图4相比，对于浅部异常源而言，当勘探区域内仅为孤立异常源时，滑动窗口尺寸相对较大有利于欧拉反褶积提取异常源信息；但与图5相比，对于浅部异常源而言，滑动窗口尺寸相对较大易于导致式(3)引入大量干扰信息(如观测数据噪声、相邻弱异常源干扰等)。综上，当测量点距为异常源尺寸的1/10时，最优化窗口尺寸应为异常源尺寸的3倍且小于勘探区尺寸的1/2。

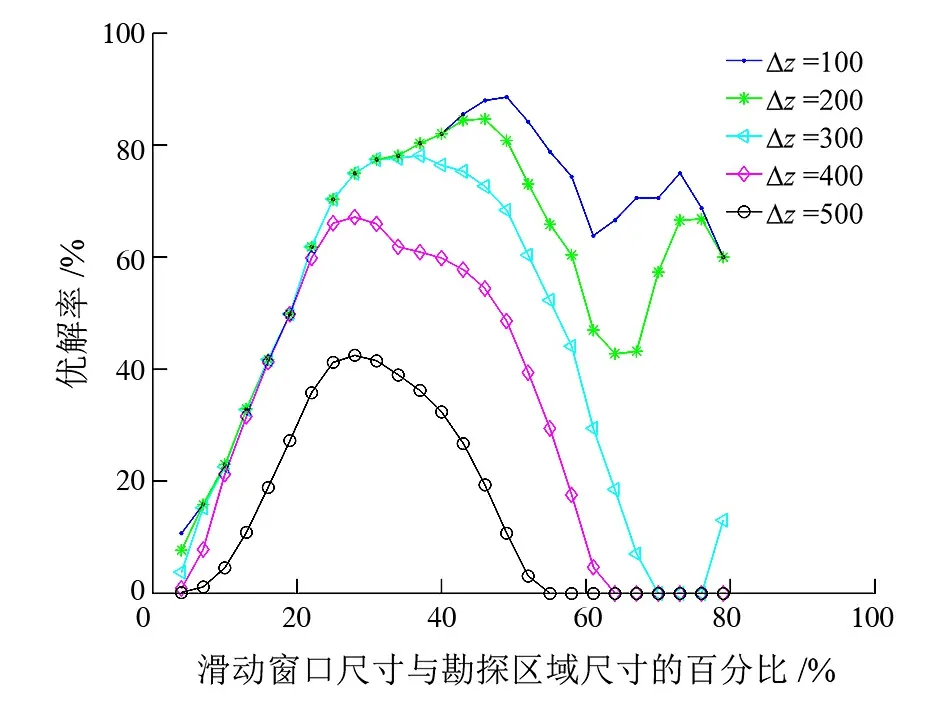
图7 浅部异常源不同尺寸滑动窗口下的优解率曲线Fig.7 Different moving windows sizes for optimal Euler solution rate of shallow anomalous sources with various offset Δz

5 结论

(1)使用单一构造指数过滤欧拉缪解，易于遗漏有用异常信息。采用估计函数εr过滤能有效的保留构造指数相对较小的欧拉解。

(2)当勘探区域大小固定时，随着滑动窗口的增大，有解率先增大后变小，当滑动窗口尺寸约为勘探区域尺寸的1/3～1/2时，有解率最大。

(3)对于孤立异常源而言，随着滑动窗口的不断增大，欧拉反褶积的优解率先稳步增大后趋于稳定；当滑动窗口很小时，浅部异常源对应的优解率占优；随着滑动窗口的不断增大，这一关系仍然得以保持；当滑动窗口尺寸大于勘探区域尺寸的1/2时，不同深度异常源对应的优解率趋于一致。

(4)对于有不同深度异常源的组合模型而言，随着异常源深度的增加，优解率在不断地降低；由于深部异常属于弱异常源，其位场总场效应相对较小，因而滑动窗口尺寸过大易于导致欧拉反褶积难以提取有效异常。对于浅部异常源而言，滑动窗口尺寸相对较大易于引入大量干扰信息。因而在欧拉反褶积中，当测量点距为异常源尺寸的1/10时，最优化窗口的尺寸应为异常源尺寸的3倍且小于勘探区尺寸的1/2。