周期开孔约束阻尼板的有限元建模与阻尼特性分析

房占鹏，刘志奇，侯俊剑，冉凯文

（郑州轻工业大学河南省新能源汽车轻量化设计与制造工程研究中心,河南 郑州450002）

1 引言

粘弹性阻尼材料不仅具有重量轻、成本低、可靠性高、易于实现的优点，而且具有良好的噪声和振动控制能力，被广泛应用于汽车、船舶、航空航天等领域［1］。通过对粘弹性阻尼材料减振机理深入分析,局部覆盖的阻尼结构更适用于工程应用的结构。周期开孔阻尼结构作为局部覆盖阻尼结构的一种,具有构型规整,对特定频段具有很好的减振降噪效果等特点［2］。文献3］对周期开孔自由阻尼管道结构进行了有限元建模，对比了全覆盖自由阻尼管道和周期开孔的自由阻尼管道的振动响应，结果表明：在某一频段内，某一频段内，周期开孔自由阻尼管道结构的减振响应比全覆盖结构的减振响应有明显的下降。周敬东等［4］研究了周期性开孔阻尼夹层板结构的声辐射特性，分析了开孔率和周期数对周期性开孔阻尼夹层板结构声辐射特性的影响。文献［5］针对传统大块敷设阻尼虽能提高隔声量，但不利于轻量化的问题，提出了二维周期阻尼结构并分析了阻尼块分布、形状等参数对薄板隔声特性的影响。在以上研究中，采用传统的有限元方法在对周期开孔的阻尼结构建模，保证计算精度，需对有限元网格细化，使建立的有限元模型单元数多，动力学分析时计算效率低。

均匀化方法广泛应用于材料的性能预测、拓扑优化和材料设计等领域。文献［6］采用均匀化理论计算了复合材料的存储模量和损耗模量，在此基础上，采用双向渐进优化算法（BESO）对粘弹性复合材料的微观构型进行了优化。文献［7］研究了粘弹性阻尼材料的最佳微观构型，改善了宏观约束阻尼梁结构的阻尼特性。文献［8］对粘弹性阻尼材料的微观结构进行了优化，有效地衰减了粘弹性阻尼结构的瞬态响应。文献［9］利用均匀化理论计算了周期胞元的等效性能，依据此对宏观的粘弹性阻尼结构进行了动力学分析，对周期胞元的布局进行了优化，以提高宏观结构的固有频率和阻尼特性。当前的研究大多集中于粘弹性阻尼层的截面由二维周期胞元构成的粘弹性阻尼结构，对截面的二维周期胞元进行均匀化分析和构型优化，对于周期开孔的约束阻尼板结构（如图1）的均匀化分析和建模研究还比较少。

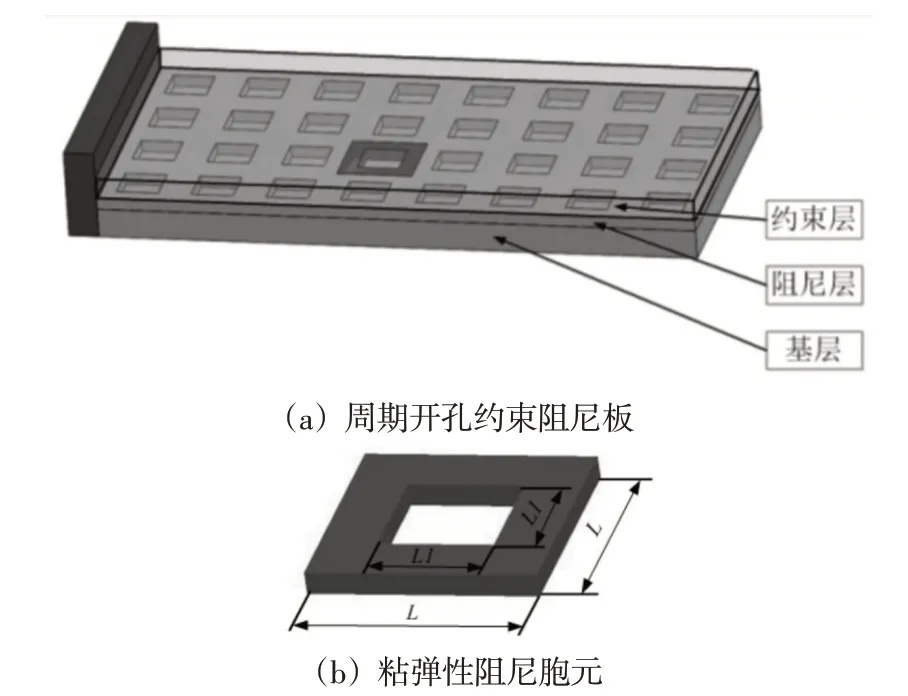
图1 周期开孔约束层阻尼悬臂板Fig.1 The Cantilever CLD Plate with Periodically Perforated Damping Material

以周期开孔约束阻尼板为研究对象，首先，采用8节点实体单元建立粘弹性阻尼胞元的有限元模型，基于均匀化理论对粘弹性阻尼胞元的等效特性进行分析，得到均匀化本构矩阵；然后，建立周期开孔约束阻尼板的有限元模型并对其进行求解，得到了周期开孔约束阻尼板的固有频率和损耗因子，最后分析了粘弹性阻尼层的剪切模量和厚度、约束层厚度和开孔率对其阻尼特性的影响。

2 粘弹性阻尼胞元的均匀化分析

约束阻尼结构的耗能主要靠粘弹性阻尼层产生的横向剪切变形，采用均匀化方法对粘弹性阻尼层胞元的等效特性分析时，需对等效横向剪切弹性模量进行计算，因而，采用8节点实体单元对粘弹性阻尼层胞元建模，均匀化本构矩阵为：

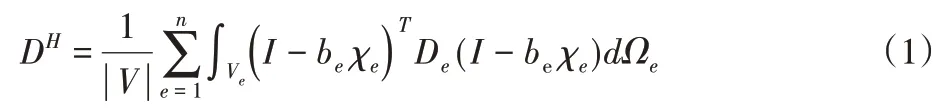
式中：I—6×6单位矩阵其可通过求解式（2）得到。

式中：n—粘弹性阻尼胞元的单元数，be、De和Ωe—单元e的应变矩阵、本构矩阵和体积，εi—给定的应变，其取值：ε1=(1,0,0,0,0,0)T，ε2=(0,1,0,0,0,0)T，ε3=(0,0,1,0,0,0)T，ε4=(0,0,0,1,0,0)T，ε5=(0,0,0,0,1,0)T，ε6=(0,0,0,0,0,1)T。在求解式（2）时，需加入周期性边界条件，并引入固定位移约束。

当粘弹性阻尼胞元为横观各向同性材料时，均匀化本构矩阵可表示为。

粘弹性阻尼胞元的等效密度可表示为：

3 周期开孔约束阻尼板的有限元模型

采用均匀化分析得到粘弹性阻尼胞元的均匀化本构矩阵之后，建立周期开孔约束阻尼板的有限元模型。周期开孔约束阻尼板的有限元模型采用4节点的复合单元，单元每个节点有7个自由度［10］。基于Hamilton原理，建立周期开孔约束阻尼板的动力学方程为：

式中：m—周期开孔约束阻尼结构的单元数基板和约束层的质量矩阵和刚度矩阵，计算方法详见参考文献［10］。根据粘弹性阻尼胞元的均匀化本构矩阵，周期开孔粘弹性阻尼层的等效质量矩阵等效刚度矩阵和等效剪切刚度矩阵可表示为：

式中：N—对应单元节点自由度的形函数，B—应变矩阵，Nγxz和Nγyz—粘弹性阻尼层剪切应变γxz和γyz的形函数向量。粘弹性阻尼层的等效本构矩阵DHv可由式（3）获得，其为：

粘弹性阻尼材料采用复常数剪切模量模型，根据文献［6］的分析，等效的复常量剪切弹性模量可表示为：

式中：ηv—粘弹性阻尼材料的损耗因子。

4 算例分析

4.1 阻尼特性分析

为了验证周期开孔约束阻尼板减振的有效性和文中建模方法的正确性，考虑一矩形周期开孔约束层阻尼悬臂板，对其阻尼特性分析。周期开孔约束阻尼板的长和宽分别为0.2m和0.1m。粘弹性阻尼层由20×10个胞元组成，胞元中心开有方孔，如图1（b）所示，开孔率p=(L1/L)2，其中L1和L分别为方孔的边长和胞元的边长，通过改变方孔的边长即可得到不同的开孔率，本算例的开孔率为1/9。粘弹性阻尼材料的剪切模量、密度、泊松比和损耗因子分别为：13.38 MPa、1200kg/m3、0.495和0.5，厚度为0.5 mm，开孔率为50%。基层和约束层均为铝，其弹性模量、密度和泊松比分别为：70 GPa、2700 kg/m3和0.3，其厚度分别为2mm和0.5mm。周期开孔约束阻尼板的一短边固支，其它边自由。

采用本文提出的建模方法，首先建立粘弹性阻尼胞元的有限元模型，对其进行静力学分析，得到等效的粘弹性阻尼胞元的本构矩阵。在建立周期开孔的约束阻尼板的有限元模型时，将粘弹性阻尼层视为均匀材料，不用考虑粘弹性阻尼层的具体结构。而采用传统的有限元方法对周期开孔的约束阻尼板建模时，为了保证计算精度，就必须根据粘弹性阻尼层的具体结构进行网格细化，其单元数就会大大增加。

采用本文提出的方法建立周期开孔约束阻尼板的有限元模型，其单元数为200个。而采用文献［10］的有限元方法建立细划分网格的周期开孔约束阻尼板的有限元模型，为了保证计算精度，其单元数为1800个。分别对有限元模型进行模态分析并提取基板层、粘弹性阻尼层和约束层的模态应变能，根据模态应变能的方法，第r阶模态损耗因子ηr可由下式计算得到：

将文献［10］和本文提出的方法计算得到的前三阶固有频率及模态损耗因子进行对比，如表1所示。

表1 前三阶固有频率和模态损耗因子Tab.1 The First Three Natural Frequencies and Mode Loss Factors

从表1可以看出，本文计算的固有频率与文献［10］的计算频率相差很小，三阶固有频率的误差最大，其为1.13%，一阶模态损耗因子的误差最大，误差为6.09%，其主要是因为粘弹性阻尼胞元开孔率为1/9时，等效剪切模量为10.5MPa，在此处，一阶模态损耗因子对剪切模量的变化较为敏感。等效剪切模量的计算误差导致一阶模态损耗因子计算误差较大。计算采用的电脑处理器为“Intel（R）Core i7”，内存为16GB，本文提出的方法计算时间为0.89秒，而文献［10］细划分网格的方法计算时间为8.15秒。可以看出，在对周期开孔的约束阻尼板进行动力学分析时，本文提出的方法计算效率远高于传统的有限元方法。

4.2 粘弹性阻尼材料剪切模量和开孔率对阻尼特性的影响

对于约束阻尼结构，存在最佳的粘弹性阻尼材料剪切模量使各阶次模态损耗因子最大［6，11］，如图2所示。

图2 模态损耗因子随剪切模量的变化Fig.2 The Modal Loss Factor Varies with the Shear Modulus

粘弹性阻尼层的剪切模量从3.34MPa逐步增加到33.4MPa，开孔率从10%逐步增加到90%，其他参数不变，分别对建立的约束阻尼悬臂板的有限元模型进行模态分析，并采用模态应变能的方法计算结构的模态损耗因子。约束阻尼悬臂板前三阶模态损耗因子的变化分别，如图3～图5所示。

图3 一阶模态损耗因子变化Fig.3 Variation of the First Order Modal Loss Factor

从图3可以看出，在研究的剪切模量的范围内，随着剪切模量的减小和开孔率的增大模态损耗因子逐渐增大。其原因是当前研究的剪切模量大于使一阶模态损耗因子最大的最佳剪切模量，粘弹性阻尼层开孔率的增大使其等效剪切模量减小，从而使等效剪切模量更接近于最佳剪切模量。

从图4可以看出，当剪切模量为3.34MPa时，全覆盖结构二阶损耗因子最大，当剪切模量为6.68MPa-33.4MPa时，二阶模态损耗因子存在峰值，并且随着剪切模量的增大，二阶模态损耗因子峰值所对应的开孔率也逐渐增大，因为随着开孔率的增大，等效剪切模量减小从而更接近于最佳的剪切模量所致。三阶模态损耗因子的变化也具有同样的规律，如图5所示，只是三阶模态损耗因子的最佳剪切模量小于二阶模态损耗因子的最佳剪切模量，当剪切模量大于26.72Mpa时，开孔率为90%时等效剪切模量仍大于三阶模态损耗因子的最佳剪切模量，因而，三阶模态损耗因子一直是增大的趋势。

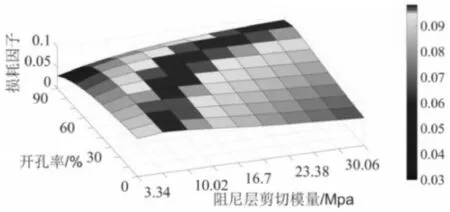
图4 二阶模态损耗因子变化Fig.4 Variation of the Second Order Modal Loss Factor

图5 三阶模态损耗因子变化Fig.5 Variation of the Third Order Modal Loss Factor

综合以上分析，当粘弹性阻尼层材料的剪切模量大于最佳的剪切模量时，可以通过周期开孔的方式，使等效剪切模量接近于最佳剪切模量，在减轻阻尼材料使用量的情况下，有效提高结构的阻尼特性。

4.3 粘弹性阻尼层厚度和开孔率对结构阻尼特性的影响

粘弹性阻尼层厚度从0.3mm逐步增加到2mm，粘弹性阻尼层剪切模量为13.38MPa，开孔率从10%逐步增加到90%，其他参数不变，分别对建立的约束阻尼悬臂板的有限元模型进行模态分析，并采用模态应变能的方法计算结构的模态损耗因子。前三阶模态损耗因子的变化分别，如图6～图8所示。

图6 一阶模态损耗因子变化Fig.6 Variation of the First Order Modal Loss Factor

从图6可以看出随着粘弹性阻尼层的厚度增大和开孔率的增大，一阶模态损耗因子都是增加的趋势，其原因是粘弹性阻尼层的剪切模量远大于使一阶模态损耗因子最大的最佳剪切模量，随着开孔率的增大，等效剪切模量逐步减小从而更接近于最佳的剪切模量，从而使一阶模态损耗因子更大。

从图7可以看出，粘弹性阻尼层的厚度为0.3mm-1.1mm时，随着开孔率的增加二阶模态损耗因子先逐渐增大，并出现峰值，开孔率进一步增大时，二阶模态损耗因子则减小；随着粘弹性阻尼层厚度的增加，二阶模态损耗因子峰值所对应的开孔逐渐变小。粘弹性阻尼层的厚度为1.3mm-2mm时，随着开孔率的增大，二阶模态损耗因子逐步减小。主要是因为随着粘弹性阻尼层厚度的增大，使二阶模态损耗因子最大的最佳剪切模量也增大。三阶模态损耗因子变化也具有同样的规律，如图8所示，不同的是，粘弹性阻尼层的厚度为0.3mm-1.3mm时三阶模态损耗因子有峰值，并且三阶模态损耗因子峰值所对应的开孔率比二阶模态损耗因子峰值所对应的开孔率要小（如表2所示），因为三阶模态损耗因子的最佳剪切模量小于二阶模态损耗因子的最佳剪切模量。

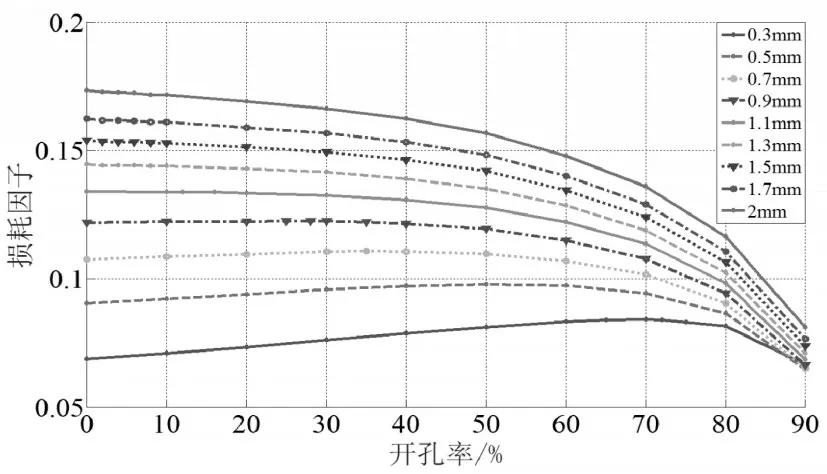
图7 二阶模态损耗因子变化Fig.7 Variation of the Second Order Modal Loss Factor

图8 三阶模态损耗因子变化Fig.8 Variation of the Third Order Modal Loss Factor

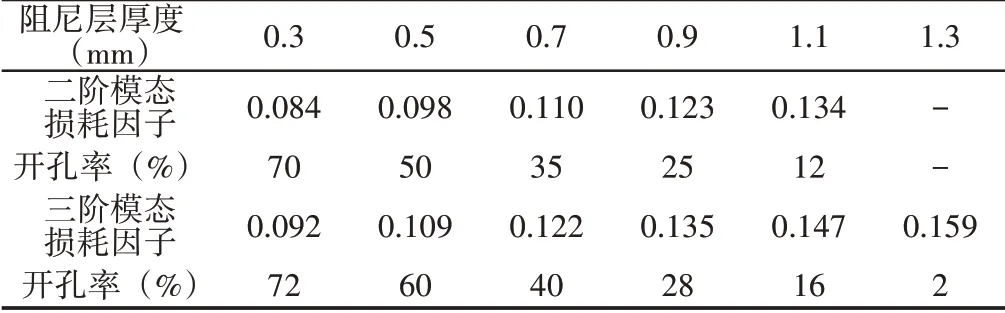
表2 模态损耗因子的峰值及对应的开孔率Tab.2 The Peak Value of The Modal Loss Factor and the Corresponding Opening Rate

5 结论

以周期开孔约束阻尼板为研究对象，采用8节点实体单元建立粘弹性阻尼胞元的有限元模型，基于均匀化理论对粘弹性阻尼胞元的等效特性进行分析；建立周期开孔约束阻尼板的有限元模型并对其进行了阻尼特性分析，研究了周期开孔阻尼板的结构参数对其阻尼特性的影响。得到如下结论：

（1）基于均匀化理论建立的周期开孔阻尼板有限元模型，由于周期开孔的阻尼层视为具有横观各向同性的均匀材料，不需要考虑粘弹性阻尼层具体结构，因而，与传统有限元建模方法比较，可有效减小有限元单元数量，可有效提高周期开孔阻尼板有限元模型在动力学分析的计算效率。

（2）通过对周期开孔的粘弹性阻尼层均匀化分析，将开孔率与材料等效剪切模量对应起来。当粘弹性阻尼材料的剪切模量大于最佳的剪切模量时，可以通过周期开孔的方式，使等效剪切模量接近于最佳剪切模量，在减轻阻尼材料使用量的情况下，有效提高结构的阻尼特性，并且粘弹性阻尼材料的剪切模量越大，最佳开孔率也越大。

（3）分析了粘弹性阻尼层厚度和开孔率对结构阻尼特性的影响，对于模态损耗因子出现峰值的阶次，随着粘弹性阻尼层厚度的增加，模态损耗因子峰值所对应的开孔率逐渐减小。