基于深度学习的小学数学模型思想建构——以图形与几何的教学为例

江苏省昆山市玉峰实验学校 顾英杰

“模型思想”是《义务教育数学课程标准（2011 年版）》提出的十大核心概念之一，也是新增加的一个核心概念，它指出“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径”。深度学习更多注重学习者积极主动，深层次理解、构建和迁移知识的学习状态和过程，更注重学习者自身对学习意义的探索，进而促成学习者学会自主学习。本文以图形与几何的教学为例，谈一些实践和思考。

一、深度学习下的感知与体验

数学模型都是具有生活背景的，特别是图形与几何的教学，教师可以从生活中找到数学实例充分利用，将情境与生活结合起来设计有效的教学活动，在感知与体验中自然建构模型。如在“用数对确定位置”一课的教学中，可设计如下教学活动：

环节一：在直线上确定位置（一维）

师：这是一堵白色的墙壁，墙上爬来了一只蜘蛛。如果要表示出蜘蛛现在的位置，可以怎么表示呢？（蜘蛛爬到底边离左边较近处，这时学生有不同的描述）

师：老师给你们一把尺，现在谁能说清楚蜘蛛的位置？

生：在1 厘米处。

师：我们就用1 来表示，下面请同学们快速地说出蜘蛛的位置。

生：5，3，0，2.5。

小结：看来，只要蜘蛛在这条线段上移动，我们就可以用一个数来表示它的位置。

环节二：在平面上确定位置（二维）

师：现在又来了一只蓝蜘蛛和一只黄蜘蛛，它们也爬到这堵墙上，不过，现在墙壁上没有尺了，你能在这堵墙上做些什么准备工作，使得它们一爬过去，就能快速地说出对应的位置呢？

学生自主探究，教师巡视了解，然后组织展示。

生1：我在墙壁的左边标上了数字，这样竖着看、横着看，就能看出蜘蛛的位置了。

生2：我还画出了横着的线和竖着的线，有了交叉点，看起来就更方便了。

师：在数学上，竖着的这些线叫做列，横着的这些线叫做行。现在请同学们看着墙，你能用列和行说说红蜘蛛、蓝蜘蛛和黄蜘蛛的位置吗？

学生交流，指名回答。

师：老师想特别介绍一下这只黄蜘蛛，它有一个超能力，能够瞬间移动，接下来，老师想请同学们想办法尽可能多的记录下它每次移动后的位置，总共会移动六次。

交流记录方法，引出数对。

通过设计蜘蛛上墙这一富有趣味性的生活情境，让学生真正经历了从“一维”描述到“二维”描述的过程。这样的学习过程，才是培养学生的创新思维，提升学生的创造力，引导学生进行深度学习的有效学习过程。

二、课本素材下的建模及创新

在小学阶段，不是所有的内容都适合培养学生的模型思想，需要对六个年段的教学内容进行整理和归纳，这也是我们课题研究中的一个子课题。在适合建模教学的内容中，尤其是图形与几何的教学，我们要充分利用好课本提供的素材，创造性地引导学生进行多层次的模型建构。如在“钉子板上的多边形”教学中，可以设计这样的教学活动：

师：四人小组，在钉子板上任意围出了不同的多边形，再计算出面积。下面，我们来展示不同小组的作品。比一比，看看谁计算面积的速度快。

分别展示作品，并比赛计算面积。

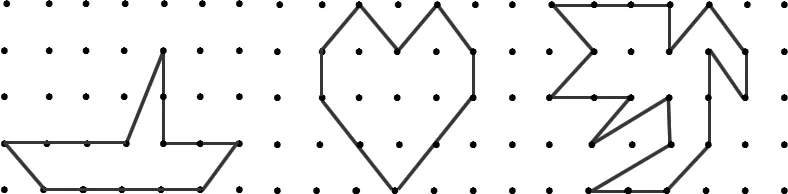
生：这里面肯定隐藏了可以快速计算面积的方法。

师：你们觉得钉子板上多边形的面积会与什么有关呢？

生1：图形边上的钉子数量。

生2：图形内部的钉子数量。

师：那钉子板上多边形的面积与它边上的钉子数和内部的钉子数到底有什么关系呢？请这一列的三组同学先分别在钉子板上围一个内部没有钉子的图形，交流讨论后填写活动单，其他几列的同学分别研究内部有一个、两个和三个钉子的图形，交流讨论后填写活动单。

各指定一组同学上台交流，并说说各组的猜想。s 表示多边形的面积，n 表示多边形边上的钉子数，a 表示内部的钉子数。

猜想一：a=0，s=n÷2-1猜想二：a=1，s=n÷2+0猜想三：a=2，s=n÷2+1猜想四：a=3，s=n÷2+2

师：现在，有了这些结论，请同学们作进一步的猜想，如果内部钉子数就是a，多边形的面积s 可以怎么表示呢？

生：s=n÷2+a-1。

师：你是怎么思考的？

生：我发现后面的数都比内部的钉子数少1。

师：你们同意这个想法吗？下面我们来进行验证，请每个小组任意选一个内部钉子数是3 以上的来进行验证。

各组分别交流各自验证的结果，最后得出结论：s=n÷2+a-1。

这样的教学，不仅使学生构建起了内容层面的模型，即“钉子板上多边形的面积=多边形边上的钉子数÷2+多边形内部的钉子数-1”，而且从方法层面构建了一个“观察猜想—操作验证—构建模型”形式化进行探究活动的方法模型。从思想层面来说，学生学会探究钉子板上的多边形这一问题并不是我们教学的最终目标，我们的目标是要让学生把探究的方法和思路进行扩展运用，从而解决一类问题。由此，引导学生进行多层次的模型构建才能真正提升学生的建模意识，从而有效地培养学生的模型思想。

三、模型思想下的探究和发现

数学建模思想下的探究和发现可以融合分类与比较的思想，借助这两者的相互结合，设计相应的教学活动，能帮助学生积累更多数学思想方法。分类与比较是确定事物异同，辨别事物相同点与不同点的基本思维过程和方法，是分析观察等活动交织在一起的复杂性智力活动。图形与几何的教学中，通过比较与分类相结合能凸显数学概念的共性与特性，帮助学生获得新的感受与体验，以及新的思维视角，从而拓展和提高对已有知识的认知度。如在“三角形的内角和”教学中，可设计这样的教学活动：

师：请第一组同学任意画一个锐角三角形，第二组同学任意画一个钝角三角形，第三组同学任意画一个直角三角形，第四组同学任意画一个三角形，用量角器量一下所画三角形的三个角的度数，并进行记录，具体内容如下：

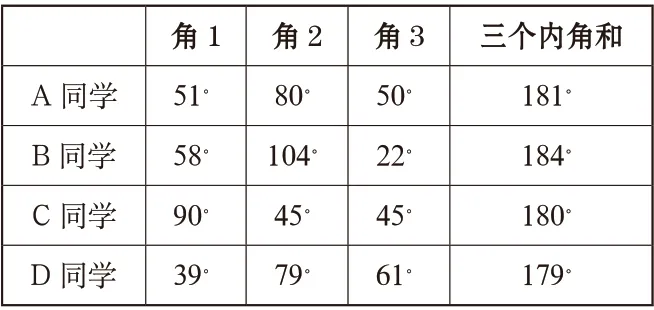
角1 角2 角3 三个内角和A 同学 51。 80。 50。 181。B 同学 58。 104。 22。 184。C 同学 90。 45。 45。 180。D 同学 39。 79。 61。 179。

师：你们发现任意三角形三个内角和有什么特点？

生：都接近180 度。

师：你们有什么好办法验证，四人小组里交流。

生1：可以通过拼接的方法验证三角形的内角和。

师：以上的验证存在误差，并不严格，谁有更好的验证方法？

生2：可以将任意三角形分割成两个直角三角形，这时我们可以发现三角形三个内角的和就是：90°+90°=180°。

师：真聪明！我们用几何画板更直观地来演示，任意拖动这个三角形的三个顶点你发现了什么？

生：通过几何画板能清楚地发现三角形内角和是180°。

这样的学习活动，将单个三角形实验研究拓展到所有三角形的研究中，能将一般与特殊相互结合起来设计教学活动，让学生对三角形以及其他图形规律有新的概括和认识。归纳出三角形内角和是180 度这一模型后，教师可以引导学生用同样的思想方法继续探索研究四边形的内角和、五边形的内角和，从而促使学生积累更多学习方法，并且适时地迁移运用拓展。

总之，教师要将模型思想有效渗透于图形与几何内容的教学中，基于深度学习，将情境与生活结合起来设计有效的教学活动，从教材提供的素材出发，引导学生从内容、方法和思想等多个层面进行思考，并结合分类与比较等多种数学思想方法进行探究和发现，才能帮助学生建立有效的数学模型，让学生逐渐形成运用模型来解决问题的习惯和技能，为终身学习和可持续发展奠定基础。