基于NSGA-Ⅲ算法的集群目标来袭火力分配建模与优化
聂俊峰, 陈行军, 苏琦
(海军大连舰艇学院 作战软件与仿真研究所, 辽宁 大连 116018)
0 引言
无人作战系统作为智能化的新型装备,具有使用灵活、全寿命费用低、作战效益高等显著特点,在军事领域应用广泛。无人机、无人潜航器、无人水面艇、无人地面车辆等无人作战系统已经成为现代战争中执行侦察监视、情报搜集、阵地防护、武装打击等任务的重要手段[1]。2018年美国国防部发布的《无人系统综合路线图(2017—2042)》,对各军种无人系统的作战需求、关键技术和无人系统之间互联互通性进行了总体规划,并指出未来各类无人系统必须具备无缝互操作能力[2]。因此,为加速战争形态向智能化演进,实现无人系统全域作战潜能最大化,无人系统的集群作战必将成为未来作战的主要形式。
上述日益复杂的作战态势对传统防御系统提出了极大的挑战,无人系统集群目标来袭的防御具有以下显著特点:首先,武器资源数量一般小于来袭集群目标数量,可通过配置合适的武器种类并选择合理的作用位置来实现火力覆盖,以达到最大杀伤效果;其次,集群目标普遍成本低廉,使得传统对其实施点对点饱和攻击效费比极低;再次,集群目标各节点之间存在互联互通,攻击目标的同时也会在一定程度上导致敌方网络节点受损,获得一定程度的网络收益;最后,集群目标呈现典型异构性,可以根据各无人系统不同性能编排组成编队,执行不同的作战任务。
火力分配是集群目标来袭防御过程中的核心决策问题,是亟需解决的关键问题。构建特定态势下的火力分配模型和开发准确高效的智能优化算法,是集群目标火力分配研究的重点和难点[3]。
在目前提出的火力分配模型中,由于单目标火力分配模型存在资源浪费、不符合实际的明显缺陷[4-5],现在主流的火力分配模型一般为多目标火力分配模型[6-8]。但多目标火力分配模型的研究重点大部分是武器数量大于目标数量的点对点饱和攻击,目标函数一般是以费效比为主,决策约束一般仅限于武器数量约束[9-11],传统的多目标火力分配模型已经不适用于集群目标来袭条件下的火力分配。因此,针对实际作战需求:张凯等[12]面向毁伤门限、安全规避、偏好指派等实际作战约束,提出了基于武器资源消耗最小和目标生存价值最小的多约束多目标火力分配数学模型;Ma[13]针对集群目标提出了涵盖目标信息、受保护对象、毁伤半径、毁伤门限等因素的约束目标聚类模型,在实例仿真中取得了较好效果。上述研究成果虽然在一定程度上深化了对集群目标火力分配问题的认知水平,但仍存在两点不足:1)模型并未充分考虑集群目标各节点之间的网络通信和武器资源自身损伤情况[14-15],未完全贴合作战实际;2)模型中对集群目标的定义表述和边界界定还比较模糊,模型的适用性仍需进一步检验。为解决以上问题,本文在充分考虑集群目标相互组网、集群目标组成异构性、集群目标个体成本低等特点的基础上,采用拓扑结构对目标攻击价值进行科学描述,以攻击效益最大、自身剩余价值最大、武器消耗最小为目标函数,以毁伤门限、武器资源总数和0-1整数约束为约束条件构建集群目标火力分配模型。
集群目标火力分配属于高维多目标优化问题。多目标进化算法是求解该类问题的有效算法,特别是非支配排序遗传算法(NSGA)系列。Deb等[16]于1995年针对遗传算法难以处理高维多目标优化问题的困境,提出了NSGA,但该算法存在计算复杂度高、效率低下等问题。基于此,Deb等[17]于2002年又提出了改进的NSGA-Ⅱ,该算法能够高效快速地求解多目标优化问题,有效降低了计算复杂度,但在3个及以上目标的高维多目标优化问题的研究中,基于拥挤度算子的NSGA-Ⅱ存在收敛性不足的缺陷。为此,Deb 等[18]于2014年提出了面向参考点选择机制的NSGA-Ⅲ,该算法在解决目标数目较多的高维多目标优化问题中取得了很好的效果。作为求解多目标优化问题的新算法,NSGA-Ⅲ具有很好的适应性,在提升运行效率、增加解空间的多样性、降低计算复杂度等方面具有显著优势,有效弥补了其他方法的诸多不足。有相关研究表明,NSGA-Ⅲ在求解3个及以上目标优化问题时表现优异:马武彬等[19]建立了以资源服务中心计算及存储资源利用率、负载均衡率和微服务实际使用率等为优化目标的微服务组合部署与调度最优化问题模型,并提出基于NSGA-Ⅲ的求解方法,在全部满足用户服务请求的约束下,该策略取得了很好的效果;蒋宁等[20]针对换热网络高维多目标优化问题,比较了NSGA-Ⅱ与NSGA-Ⅲ在实际应用中的性能,结果表明,一定条件下NSGA-Ⅲ比NSGA-Ⅱ求解收敛困难的高维多目标优化问题更具优势。
基于以上论述,本文首先构建集群目标来袭多目标多约束火力分配模型;进而基于NSGA-Ⅲ对集群目标火力分配优化进行实现;最后通过仿真实验对算法的有效性进行验证。结果表明,NSGA-Ⅲ在求解集群目标火力分配优化问题时具有更好的运行效率和收敛能力。
1 集群目标火力分配建模
1.1 模型假设
假设m个武器资源参与作战,拦截n个来袭集群目标,对应的问题变量为:己方武器集合W={w1,w2,…,wi,…,wm};目标个体集合T={t1,t2,…,tj,…,tn};目标位置集合L={l1,l2,…,lj,…,ln};武器的成本向量E=(e1,e2,…,ei,…,em);目标个体的价值向量V=(v1,v2,…,vj,…,vn);目标之间通过可靠网络相连,目标个体tj1与tj2之间的网络通信能力为dj1j2∈[0,1];第i号武器打击目标时自身损伤概率为hi;目标收益、网络收益权重分别为γt、γn.
决策变量为:武器决策向量X=(x1,x2,…,xi,…,xm),xi∈[0,1];武器作用点集合Cp={cp1,cp2,…,cpi,…,cpm}。
集群目标火力分配网络结构示意图如图1所示,图1中:Ri为武器wi的杀伤半径。

图1 集群目标火力分配网络结构示意图Fig.1 Weapon-target assignment network topology for the group targets defense
1.2 目标函数
基于拦截效益最大化、自身剩余价值最大化、武器消耗最小化3个目标函数构建集群目标火力分配模型。
1)目标拦截效益最大化函数。目标的拦截效益由攻击敌方目标得到的直接收益和导致敌方目标网络节点受损所获得的间接收益两部分构成[14]:

(1)
式中:D为目标坐标杀伤规律,在计算中一般用简化圆概率误差(CEP)[12]表示;gj1j2为tj1和tj2之间的连通性,gj1j2=1表示对tj1和tj2中任一目标的毁伤概率大于门限条件,否则gj1j2=0.
2)自身剩余价值最大化函数为
(2)
式中:ε(xi)为阶跃函数。
3)武器消耗最小化函数为
(3)
1.3 约束条件
集群目标火力分配不仅需要考虑资源总数、资源整数等基本约束,还需考虑毁伤门限等实际约束。
1.3.1 武器资源数量约束
武器资源总数和0-1整数约束为集群目标火力分配模型中的基本约束条件,资源数量之和不超过武器资源总数,且各武器资源仅存在已消耗和未消耗两种状态:
(4)
1.3.2 毁伤门限约束
为限制敌方某些关键目标节点的效能发挥,作战指挥系统往往期望将其生存概率压制于设定毁伤门限值之内[12]:
(5)
式中:α为满足不等式‖lj-cpi‖≤Ri的数量;ρ=(ρ1,ρ2,…,ρj,…,ρn),ρj为目标tj的预设毁伤门限值,0≤ρj≤1,ρj=1表示对目标tj无门限值要求。
1.4 数学模型
综上所述,构建的集群目标火力分配数学模型为
max(yt,ys,-yc),
(6)
(7)
根据(6)式和(7)式可知,集群目标火力分配数学模型属于混合整数非线性多目标优化范畴,难点在于多目标问题Pareto前沿的求解。另外,由于多约束条件的存在,也对寻优算法提出了更高要求。
2 基于NSGA-Ⅲ的集群目标火力分配优化
基于NSGA-Ⅲ求解集群目标火力分配优化问题的关键内容可分为种群初始化、非支配排序、参考点机制和性能度量4个部分。
2.1 种群初始化
种群初始化包括编码和生成初始种群两部分:
1)采用连续实数编码方式,种群个体为武器资源使用情况及作用点。
2)初始种群需具备均匀性、多样性和可行性。需在生成大量满足约束条件的均匀分布随机个体的前提下,遴选性能最优的个体形成初始种群。
2.2 非支配排序
1)随机生成种群At,通过随机选择、模拟二进制交叉和多项式变异生成子种群Bt.
从父代种群中随机选取个体P1、P2,进入交叉操作后,其子代个体Q1、Q2可计算为
(8)
式中:β与随机数μ∈[0,1]有关,公式为
(9)
ηc为交叉分布指数,ηc越大,子代个体与父代越相近。
若进入变异操作,则从父代种群中随机选取个体P3,变异产生其子代个体Q3的公式为
(10)
式中:ηv为变异分布指数,可依据进化情况予以调整;xmax、xmin分别为变量x的上、下边界。
2)父代种群At和子代种群Bt合并为Rt,|At|=N,|Bt|=N,|Rt|=2N.
3)构建新种群St,将Rt划分为若干不同非支配层(F1,F2,…),自F1开始,将各非支配层的解依次填充到St,直至|St|≥N.若最终可接受的非支配层是第O层,则舍弃在第O+1层及之后的解。
2.3 参考点机制
NSGA-Ⅲ采用参考点机制保持种群的多样性[20],归一化操作是参考点机制的核心[18],具体步骤如下:
1)生成参考点。基于Das等[21]提出的正交边界交叉算法生成参考点。
2)计算理想点。针对U维的多目标优化问题,理想点集Zmin可定义为种群在目标每个维度上最小值zi,min的集合。
Zmin=(z1,min,z2,min,…,zU,min).
(11)
3)转译目标值。转译种群S′t的目标值f′i(x)为
f′i(x)=fi(x)-zi,min,x∈St.
(12)
4)计算极值点zi,max.通过标量化函数计算第i维目标的极值点zi,max为
(13)
式中:ωi=(ε,ε,…,ωi,i,…,ε),ωi,i=1,ε=10-6.
5)构建线性超平面,其通用方程为
A1x1+A2x2+A3x3+…+AUxU=1,
(14)
式中:A1,A2,…,AU为不全为0的常数;x1,x2,…,xU为超平面上任意一点坐标。
输入每个维度上的极值点Zmax即可构建超平面,并可计算超平面截距ai.
6)种群目标值归一化,可表示为
(15)
式中:i=1,2,3,…,U;上标n表示归一化;x∈St或S′t.
7)关联参考点。将距离种群个体最近的参考线对应的参考点定义为与该个体关联。
8)个体选择。基于小生镜保留操作进行个体选择[22-23],直到满足种群规模。
三维目标的参考点机制示意图如图2所示。
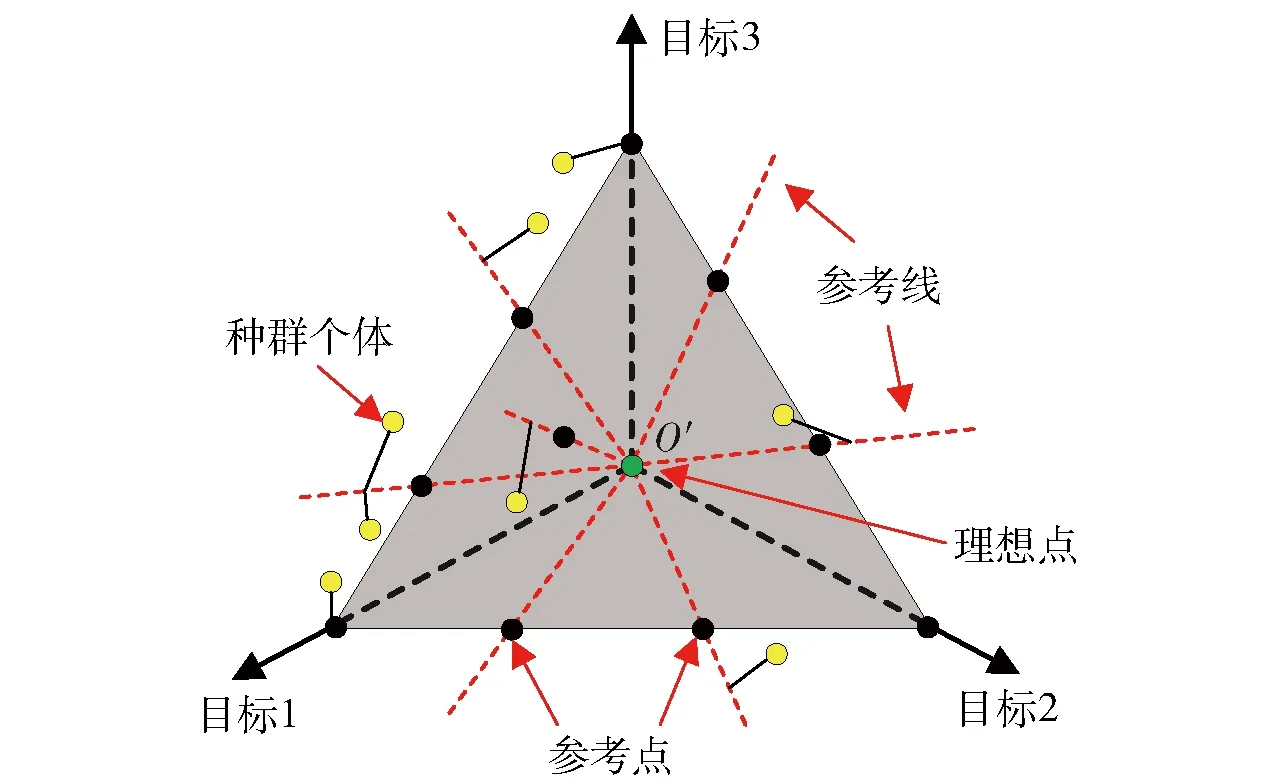
图2 三维目标的参考点机制示意图Fig.2 Reference points on a normalized hyperplane
2.4 性能度量
一般通过评估所得Pareto前沿面的收敛性和分布的均匀性对算法性能进行度量。依据Zitzler等[24]的研究结果,采用收敛性指标C和间距指标S评估。
2.4.1 收敛性指标
令P*=(p1,p2,…,p|P*|)为理想Pareto前端面上均匀分布的Pareto最优解集合,而B=(b1,b2,…,b|B|)是通过NSGA-Ⅲ得到的近似Pareto最优解集。集合B中每个解bi距离P*的最小归一化欧氏距离可计算为
(16)

(17)
式中:C值越小,得到的最优解收敛性越优。
2.4.2 间距指标
间距指标定义为
(18)

基于NSAG-Ⅲ的集群目标火力分配优化算法流程如图3所示。
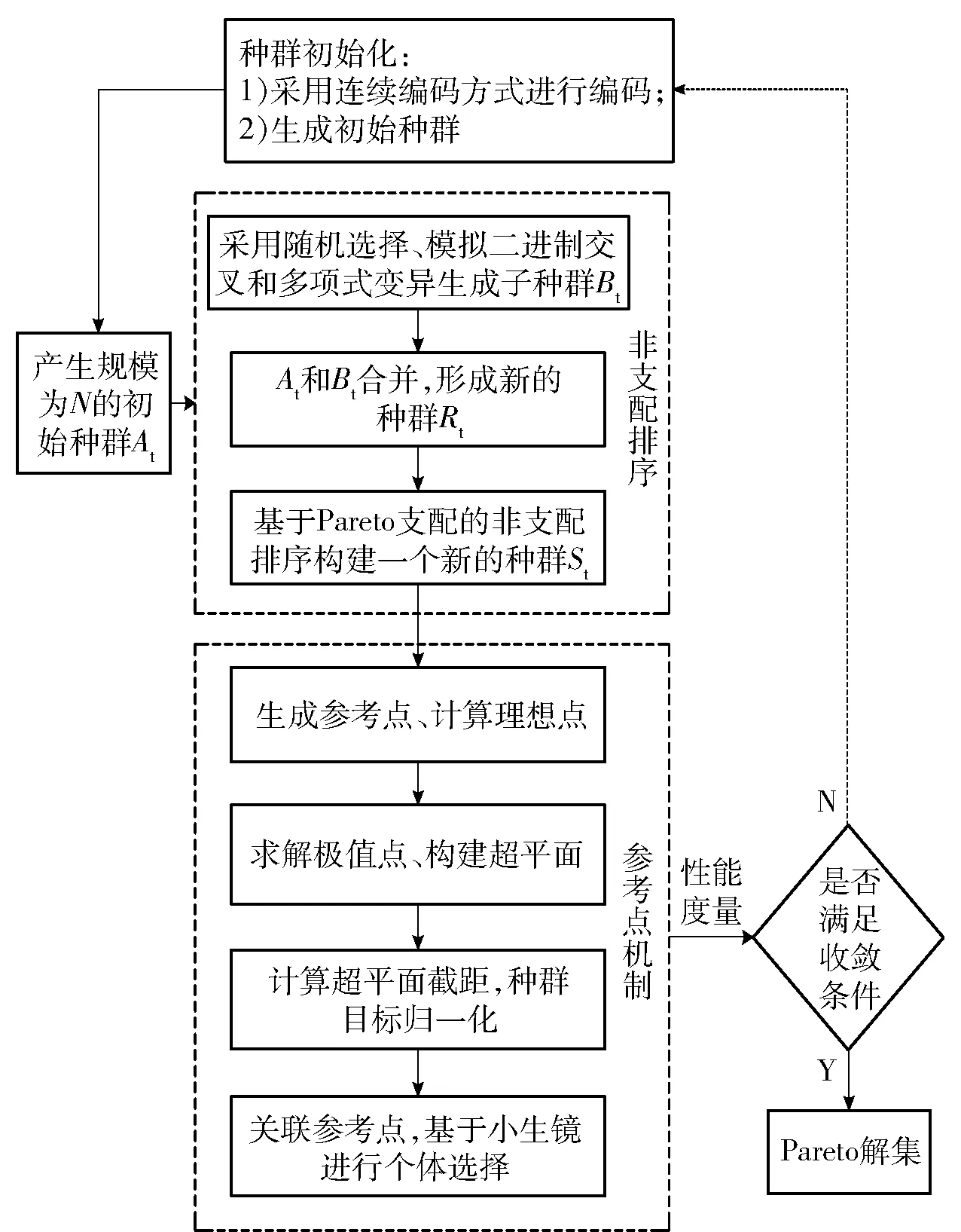
图3 基于NSGA-Ⅲ的集群目标火力分配优化算法流程Fig.3 Flowchart of optimized weapon-target assignment algorithm based on NSGA-Ⅲ
3 仿真计算及结果分析
3.1 仿真条件
为验证NSGA-Ⅲ求解集群目标火力分配优化问题的有效性,分别采用第2代强度Pareto优化算法(SPEA2)、NSGA-Ⅱ和NSGA-Ⅲ 3类具有代表性的多目标进化算法进行仿真求解,并对仿真结果进行对比分析。相关作战想定如下:假设在三维场景中,战场环境大小为10×10×10,设计3组(M1、M2、M3)仿真实验,其中M1、M2、M3中集群威胁目标个体数量分别为20个、30个、40个,己方可用武器数量均为10个。每组实验独立进行10次仿真计算,表1为威胁目标参数取值情况,表2为武器资源参数取值情况,相关数据已经归一化处理。

表1 威胁目标参数取值表Tab.1 Parameter values of threat targets

表2 武器资源参数取值表Tab.2 Parameter values of weapons
本算例中SPEA2、NSGA-Ⅱ和NSGA-Ⅲ的初始参数设置如下:
SPEA2:种群规模为50,存档集规模为50,终止代数为50,交叉概率为0.8,变异概率为0.05.
NSGA-Ⅱ、NSGA-Ⅲ:种群规模为50,终止代数为50,交叉概率为0.8,变异概率为0.05.
在Core i5 3.3 GHz、内存4 GB的计算机,MATLAB 2013a环境下进行仿真实验。
3.2 仿真结果及分析
各算法求解结果中的最优值如表3所示。

表3 各算法的最优值Tab.3 Best results of 3 kinds of algorithms
由表3可知,M1、M2、M3组求得的最优解yt、yc、ys中,虽然SPEA2与NSGA-Ⅱ各有优劣,但NSGA-Ⅲ都比SPEA2、NSGA-Ⅱ明显占优,表明基于NSGA-Ⅲ能够较好地实现集群目标火力分配优化,验证了方法的有效性。
SPEA2、NSGA-Ⅱ和NSGA-Ⅲ求解的平均计算时间如表4所示。

表4 各算法平均计算时间
由表4可知,NSGA-Ⅲ相对SPEA2、NSGA-Ⅱ,在M1组的运行时间基本持平,而在M2组和M3组的运行时间明显占优,运行效率高。一般来说,针对集群目标来袭的防御任务具有非常强的时间紧迫性,计算效率会在很大程度上影响任务的执行情况,故NSGA-Ⅲ更符合大规模集群目标来袭火力分配对时效的要求。
为定量比较SPEA2、NSGA-Ⅱ和NSGA-Ⅲ的性能指标,图4和图5分别给出了3种算法下各组C值及S值情况。

图4 SPEA2、NSGA-Ⅱ和NSGA-Ⅲ的C值对比Fig.4 Comparison of C values of SPEA2,NSGA-Ⅱ and NSGA-Ⅲ
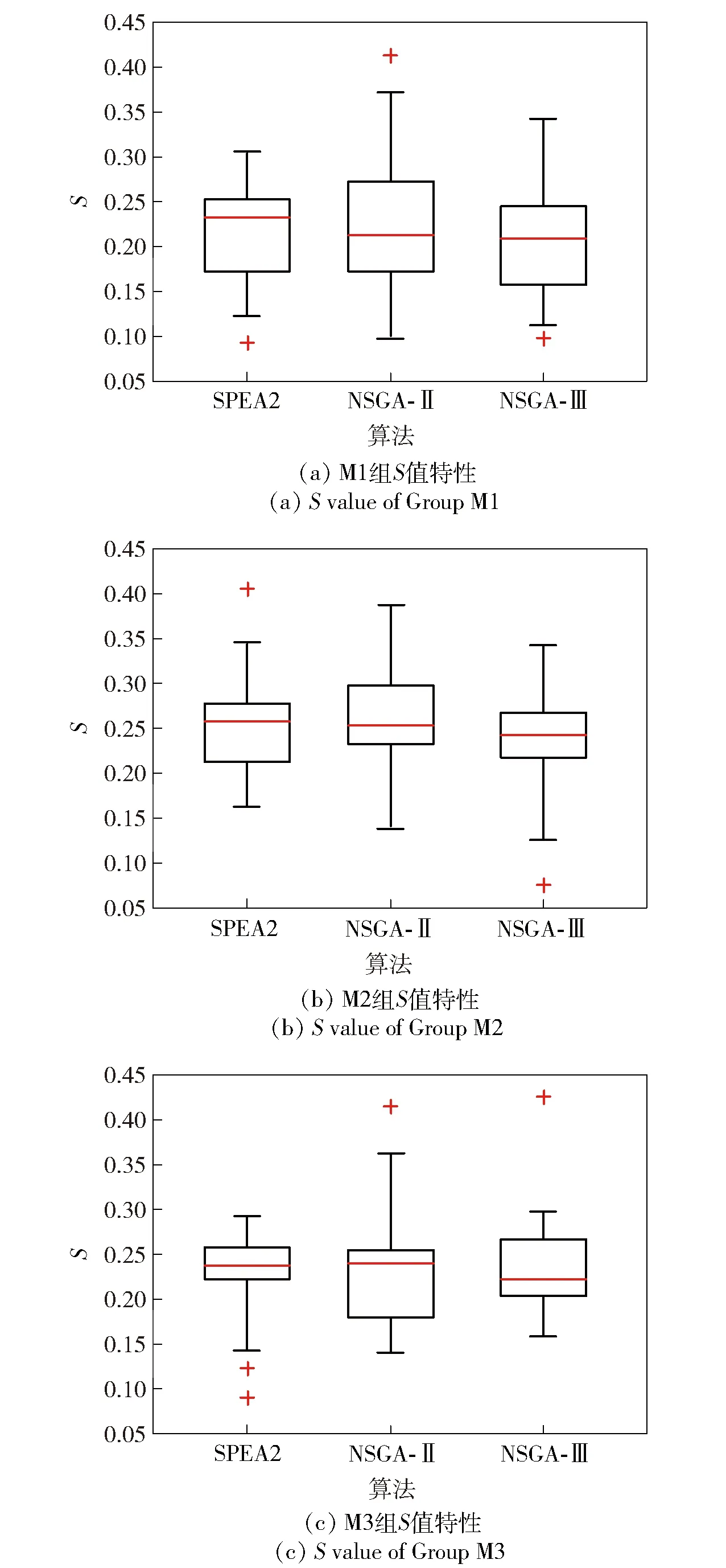
图5 SPEA2、NSGA-Ⅱ和NSGA-Ⅲ的S值对比Fig.5 Comparison of S values of SPEA2,NSGA-Ⅱ and NSGA-Ⅲ
由图4和图5可以看出,M1、M2、M3组中NSGA-Ⅲ的C值和S值都明显比SPEA2、NSGA-Ⅱ占优,表明NSGA-Ⅲ得到的近似Pareto最优解的收敛性更好,在目标空间上的分布更均匀。
4 结论
面向无人作战系统集群目标来袭条件下火力分配优化问题的研究具有重要现实意义。本文在充分考虑集群目标相互组网、集群目标组成异构性、集群目标个体成本低等特点的基础上,面向拓扑结构描述目标的攻击价值,构建集群目标下多目标多约束火力分配模型,并基于NSGA-Ⅲ对集群目标火力分配优化进行了实现。得出主要结论如下:
1)面向集群目标来袭的作战需求,以攻击效益最大、自身剩余价值最大、武器消耗最小为目标函数,以毁伤门限、武器资源总数和0-1整数约束为约束条件,构建了集群目标火力分配模型,充分考虑了集群目标来袭的特点,提高了模型的有效性和适用性,较以往模型有较大改进。
2)采用收敛性指标和间距指标对SPEA2、NSGA-Ⅱ和NSGA-Ⅲ的集群目标火力分配模型求解结果进行了对比验证,实现了闭环研究。
3)在约束可行范围内得到了分布良好的Pareto集合,可为指挥人员提供更多有价值的选择方案。

