基于卷积神经网络和模糊函数主脊坐标变换的雷达辐射源信号识别
普运伟, 刘涛涛, 郭江, 吴海潇
(1.昆明理工大学 信息工程与自动化学院, 云南 昆明 650500;2.昆明理工大学 计算中心, 云南 昆明 650500)
0 引言
雷达辐射源信号(RES)识别是电子侦察的重要组成部分,其技术水平和雷达对抗系统水平紧密相关。随着电子对抗中电磁环境愈加复杂以及复杂体制雷达的迅速发展,传统仅依靠常规脉冲描述字的5个特征,即到达时间(TOA)、载波频率(RF)、到达方向(DOA)、脉冲幅度(PA)和脉冲宽度(PW)的分选方法已经无法满足实际战场的需要,寻找新的分选识别特征参数已成为解决该问题的重要研究方向。另一方面,随着对辐射源信号先验信息认知的增强,利用新型学习算法对RES进行分选识别成为了一种可行的研究方案。
近年来,国内外专家学者对提取雷达信号的脉内特征进行了重点研究,如时频特征[1]、小波特征[2]等并获得了一定的分选效果。但人工提取特征存在耗时长且需要研究者具有较高的知识储备等问题,因此,基于深度学习(DL)的RES识别不失为一种可行的方案。DL广泛运用于模式识别[3]、图像处理[4]等领域,DL通过多层神经网络非线性映射的堆叠来提取数据更抽象、更深层次的特征[5]。其中,卷积神经网络(CNN)因其强大的学习能力在信号处理领域已得到成熟应用。文献[6]通过Choi-William分布(CWD)得到信号的时频特征图,将其输入到调试好的CNN模型并构造Softmax分类器[5]对其多类信号进行分类,取得了较好效果。文献[7]根据信号能量在不同分数阶傅里叶变换域角度上的明显变化对信号进行分离,并通过CNN提取第一分量的平滑伪仿射维格纳变换(SPWVD)图的深层特征,准确率得到了较大提高。文献[8]提取信号的双谱信息作为CNN的输入,结果表明该方法在识别率、抗噪性上都有所提升。但以上方法存在耗时长、损失的信息较多等问题,同时在低信噪比环境下的识别率也有待提高。
模糊函数(AF)提供了对信号结构信息较为完整的描述,包含了信号丰富的时频域信息。AF主脊(AFMR)作为模糊能量最聚集的部分,其分布信息体现了AF分布特性,因此,对AFMR进行研究有助于RES分选识别。文献[9]通过对AF三维分布进行投影获得其等高线,然后提取等高线的正外接矩、纵横比和方向角作为特征向量,该方法充分利用了一些海拔较高的AF地貌特征,但在低信噪比下AF地貌易受噪声干扰,导致分选效果不理想。文献[10]通过提取AFMR的旋转角、原点矩以及中心矩特征进行分选识别,在一定程度上描述了模糊能量分布特性且鲁棒性较高,但该方法计算量大、耗费时间长,不适用于实际战场中雷达信号的复杂环境。
本文提出一种基于CNN和AFMR极坐标变换的RES识别方法。该方法采用多个神经网络层提取AFMR极坐标域二维时频图的深层特征,然后通过反向传播(BP)算法对网络内部的权重和偏置进行微调,并通过正交设计实验对CNN中的参数进行优化,得到最优的参数组合。最后通过Softmax分类器对雷达信号进行分类识别。仿真结果表明,本文方法在识别率、耗时上均优于传统的雷达信号识别方法。
1 基于CNN和极坐标AFMR切面识别的理论基础
1.1 AFMR提取与极坐标转换
任意窄带RES用s(t)表示,s(t)的AF可以定义[10]为
(1)
式中:χs(τ,ξ)为AF,τ为时延,ξ为频移;s*(t)为s(t)的共轭,t为时间变量。AF提供了一个信号及其自身经时延和频移后所得信号间的相似性度量,反映了信号本身内在结构上的特性。
AF在原点处有最大值,因此过原点至少会有一条模糊能量的主要分布带,即为AFMR.Akay等[11]定义了AF和分数自相关运算的关系:
[Cα(s,s)](ρ)=χs(ρcosα,ρsinα),
(2)
式中:α为旋转角;Cα为主脊切面所在分数域uα上的分数自相关算子;ρ为uα分数域的径向距离。(2)式表明,旋转角为α的分数域的自相关等价于该分数域上AF的径向切面。因此,通过分数傅里叶变换的快速离散方法,便可计算AF任意过原点的径向切面。文献[10]构建了如下检测量:
(3)


图1 6类RES AFMR切面对比Fig.1 Comparison of AFMR slices of six types of radar signals
从图1中可以看出:无论是在信噪比为0 dB还是20 dB情况下,CON、LFM以及BFSK能明显区别于其他3类信号,而BPSK、QPSK和MSEQ则发生了混叠,这是因为该3种信号都为非线性调制信号,其中BPSK和QPSK仅仅只是相位调制的阶数不同,频域上差异不显著,因此二者的AFMR交叠明显。且信噪比0 dB时AFMR对噪声更为敏感,信号严重失真,信号间混叠更为严重。
为了解决这个问题,本文从坐标转换的角度出发,将笛卡尔坐标系的原图形映射到极坐标系当中,转换后AFMR为一个封闭的二维图像。坐标转换公式原理如下:
(4)
式中:xuα、yuα分别为AFMR在横、纵坐标轴上的值;MRS(·)为模糊函数归一化响应,因此,令uα为转换角度,MRS(uα)为半径。然而转换的二维图像有许多毛刺与突起,为了不影响图像的形状,采用两次80点滑动平均方法对图形进行降噪处理。图2所示为6类RES在信噪比为20 dB和0 dB环境下去噪后的极坐标AFMR图像。

图2 6类RES去噪后极坐标AFMR切面对比Fig.2 Polar coordinate AFMR slices after denoising of six types of radar signals
图2(a)和图2(b)与图1中相对应的图像对比可以看出,6类RES的形状、大小有明显区别,即使图像有所交叠,但CNN具有强大的学习和提取图像深层抽象特征的能力,因此采用AFMR极坐标时频图作为CNN输入的想法是可行的。
1.2 CNN基本原理
CNN由纽约大学LeCun等[12]提出,其本质是一个多层感知机,是一种带有卷积结构的深度神经网络。CNN最大的优势在于局部连接和权值共享,大大减少了网络中参数个数,有效缓解了模型过拟合问题。图3所示为假设相邻神经元节点之间是具有宽度为3的感受野时的局部连接和权值共享示意图。CNN由输入层、卷积层、激活函数、池化层以及全连接层组成。基本模型如图4所示。图4中,m表示当前层数。

图3 局部连接与权值共享Fig.3 Local connection and weight sharing

图4 CNN基本结构Fig.4 Basic structure of CNN
CNN基本结构如下:
1) 输入层:用于数据的输入。
2) 卷积层:卷积层是CNN的核心,由多个卷积核组成。卷积核以一定的步长在特征图上移动来获取图片的特征,然后传递给激活函数进行处理,激活函数将新得到的特征传递给下一层,其基本公式为
(5)
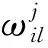
f(x)=max (0,x).
(6)
3) 池化层:激活函数输出的新特征量通过池化层进行降维,加快了计算速度,提高了模型的能力。常用的池化方法有平均池化和最大池化,由于平均池化能避免过拟合以及提高鲁棒性,故本文方法采用平均池化对特征分布进行降维。
4) Dropout层:为防止过拟合,该层使某个神经元的激活值以一定的概率停止工作。
5) 全连接层:该层的每一个节点都与上一层的所有节点相连,用来把前边提取到的特征综合起来,目的是减少特征位置对分类带来的影响。
6) 输出层:该层将全连接层整合后的向量作为输入,其输出节点数等于需要分类的类别数。本文采用常用的分类器softmax进行分类识别,其不但考虑了输入的加权和,还考虑了其他输出节点的输出值,并且更适合解决多标签的情况。它把多个神经元输出看作概率值,因为输出被其映射到(0,1)之间,输出概率的数学公式如下:
(7)

6)损失函数:CNN采用损失函数计算预测值和实际输出值的差值,并通过BP算法和梯度下降算法将该误差用来更新模型中的权值和偏置。交叉熵函数作为最常用的损失函数,其计算公式如下:
E=-dln (y)-(1-d)ln (1-y),
(8)
式中:d为训练数据的正确输出;y为输出节点的输出。
1.3 正交设计
CNN中存在许多参数,比如学习率、动量、卷积核尺寸等,参数的选取直接影响到CNN的识别率,所以寻找最优的参数组合是有必要的。
正交设计是针对多个因子进行研究分析的一种方法,其理论基础是正交性与数理统计学。该方法通过科学设计的正交表进行实验,从而得到最优的参数组合。其实验流程如图5所示。
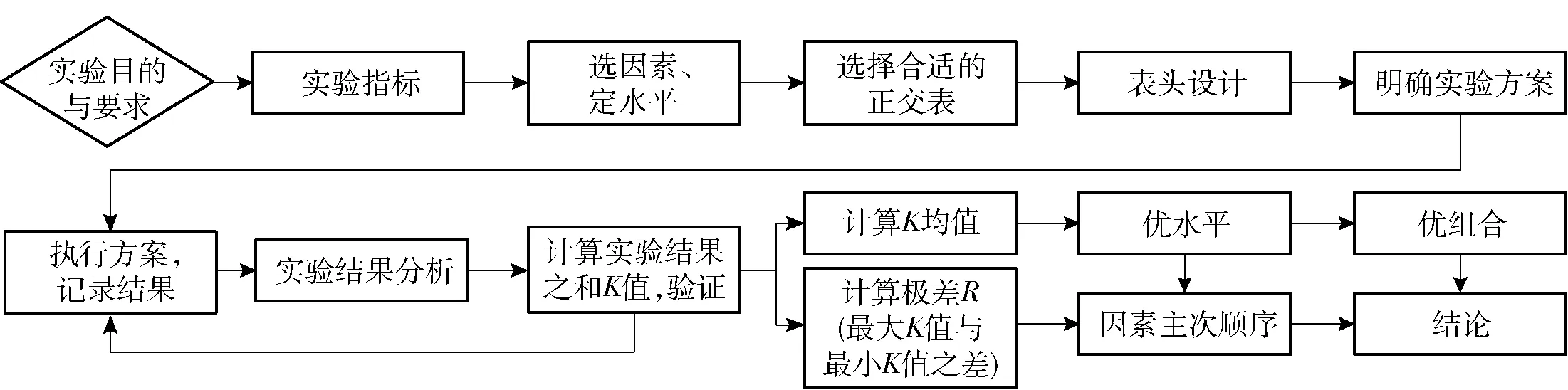
图5 正交实验流程图Fig.5 Flow chart of orthogonal test
由图5可知,正交设计主要包括实验设计和数据分析两部分,其基本步骤如下:
1)明确实验目的与要求;
2)挑选需考察的因子并确定其水平;
3)选定正交表后进行表头设计;
4)制定实验方案,执行并记录结果;
5)统计分析实验结果,确定最优组合。
2 基于CNN的极坐标AFMR切面识别方法
通过CNN学习AFMR极坐标二维时频特征分布并对信号进行分类识别的算法流程如图6所示。

图6 基于CNN和AFMR极坐标图的识别模型Fig.6 Recognition model based on CNN and AFMR polar diagram
具体步骤如下:
1)数据预处理:为保证所有信号相同长度,将RES长度重采样为N=1 024;为了提高计算速度,对所有极坐标图像作灰度化处理成维度为300×300×1的统一格式来作为CNN的输入。
2)模型搭建:CNN提取特征过程中,使用的卷积核大小为(7,7)且滑动步长为1,卷积核个数分别是6和12. 批归一化层目的是把每一层的输出均值和方差归一化,不仅加快了模型的收敛速度,而且缓解了网络梯度弥散的问题。池化层均采用大小为(2,2),滑动步长为2的平均池化进行特征降维。在卷积部分完成后,图像尺寸由300×300压缩成72×72. 具体按照表1中所示的各层详细参数构造CNN.

表1 CNN模型的细节和参数Tab.1 Details and parameters of CNN model
3)模型预训练:在前向传播时,Dropout层使某个神经元的激活值以一定的概率停止工作,而不是仅仅依赖某些局部特征;L2范数是指向量各元素的平方和,然后再求平方根,其将一些参数值进行缩小,使其影响变小。为了防止过拟合,在全连接层前加一个Dropout层以及在损失函数中加入L2范数作为惩罚项。初始化参数并将生成的训练集作为输入,通过BP算法和梯度下降算法对整个网络的权值和偏置进行微调。
4)分类识别:6类预处理好的辐射源信号AFMR极坐标时频图输入到搭建好的CNN网络中,进行分类识别,并输出识别结果。
3 实验结果与分析
实验选取CON、LFM、BPSK、QPSK、MSEQ和BFSK 6类典型RES. 其中,LFM的带宽为10 MHz,BPSK和BFSK都采用13位Barker码,QPSK采用16位Frank码,MSEQ所用伪随机序列(1011100),所有信号的PW均为10 μs,采样频率为60 MHz. 此外,除BFSK信号的两个频点分别取10 MHz和2 MHz外,其余信号载频均为10 MHz. 在-10~20 dB信噪比下,每类信号每隔2 dB产生20个信号样本,共1 440个信号作为训练集,每类信号在不同信噪比下各产生100个信号样本,即每个测试集有600个信号样本。
3.1 参数优化


表2 正交实验因素水平Tab.2 Orthogonal test factor level table
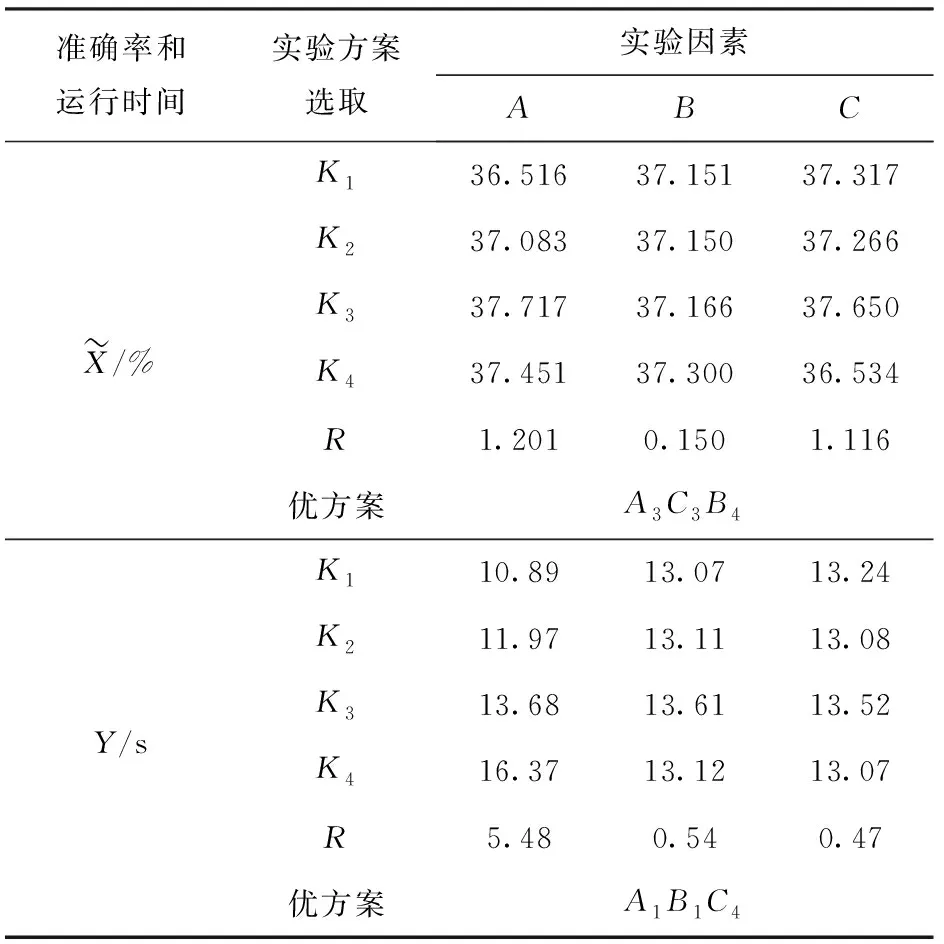
表3 实验结果分析Tab.3 Test result analysis table
如表3所示,对于准确率指标而言,结合表2可知,卷积核尺寸位于第3水平、学习率位于第4水平以及动量位于第3水平识别率最高,极差R代表因素的主次关系,R越大、因素越重要,因此准确率的最优方案为A3C3B4,同理运行时间得出的优组合为A1B1C4.然而对于RES而言,其分选的准确率最为重要,因此把准确率作为主要指标,运行一次Epoch所需的时间为次要指标。A1与A3、B1与B4、C3与C4在时间上都相差无几,最大的仅为2.79 s,然而在识别率上却相差甚远,其中A1和A3准确率相差有10%以上,考虑到准确率作为主要考察目标。因此,模型的参数最优组合为A3B4C3,将其代入到神经网络中。
3.2 本文方法与人工特征提取性能比较
本文方法与人工提取信号特征相比,CNN能够提取输入数据的隐藏抽象特征。为探究本文方法和人工提取方法在不同信噪比下的性能,选取文献[13]、文献[14]以及文献[15]3种人工方法与本文方法进行对比,结果如图7所示。
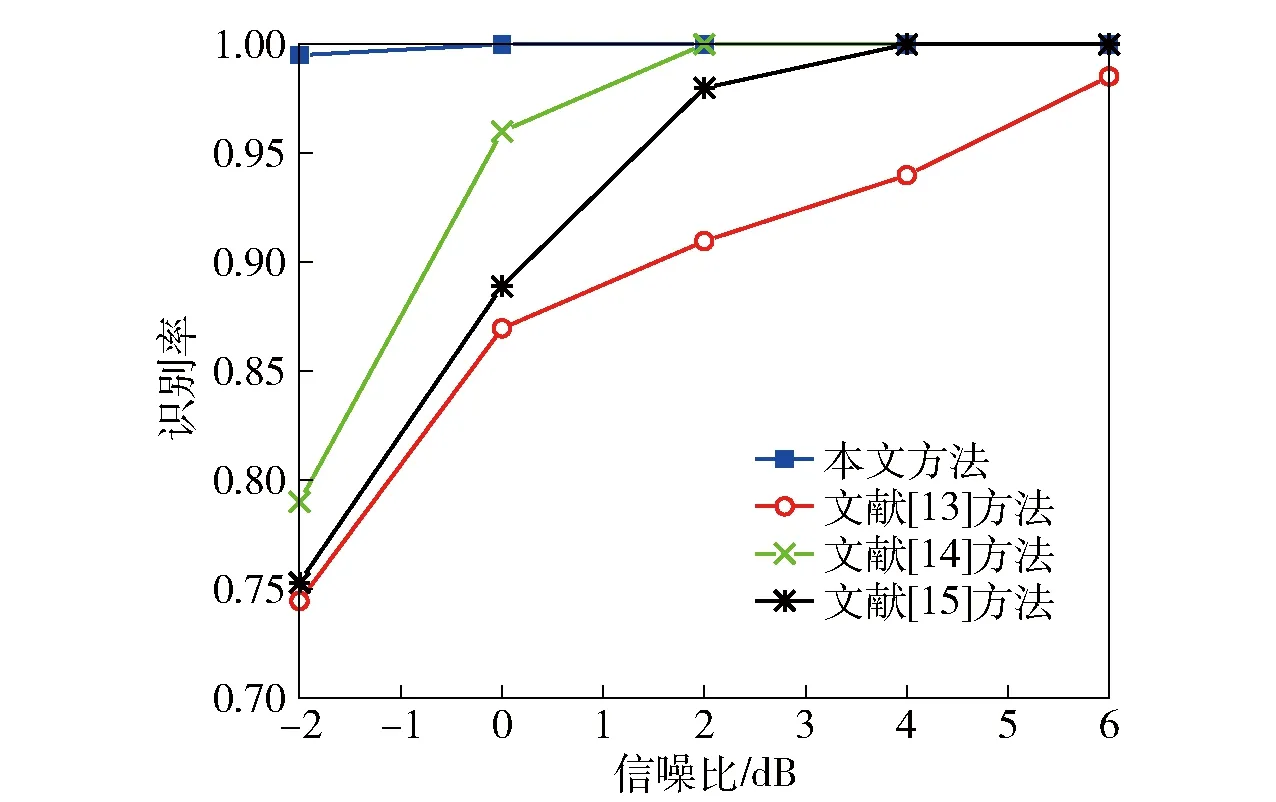
图7 本文方法与人工方法比较Fig.7 Comparison of the proposed method and manual methods
由图7可以看出:文献[13]从主视角、侧视角对AF的三维地貌进行描述,但其在低信噪比下准确率低,因为它无法同时兼顾时域和频域的信息;文献[14]使用奇异值分解对AF主脊切片包络线进行降噪,提取AF主脊切片包络线的旋转角系数和对称Holder系数作为特征,但该方法计算量大、耗费时间长,信噪比-2 dB时准确率也仅为79%;文献[15]提出的特征虽然综合了时频域的信息,但在低信噪比下其表现也不尽如人意,信噪比-2 dB时准确率为75.3%. 从这3种方法可知,人工分选方法在低信噪比下表现不佳,这是因为人工方法只能提取信号的表面信息,而信号的大部分信息在低信噪比时基本被噪声给淹没。DL虽然属于有监督学习,需要先验信息的支持,但是其能更好的描述输入信号的内在信息且鲁棒性强,抗噪性能好,大大提高了信号在低信噪比下的分选识别率。
3.3 本文方法与其他DL模型对比
为进一步探究本文方法的高效性,通过与其他的DL模型进行对比分析,结果如图8所示。

图8 本文方法与其他模型对比Fig.8 Comparison of the proposed method and other models
由图8可知:本文方法在低信噪比下识别率最高,信噪比-6 dB时也能达到94.17%,这是因为本文在对信号进行处理时几乎没有信息的损失;文献[16]虽然输入为AFMR,但是本文在此基础上进行了坐标转换,抗噪性较之有所增强,不过即便不对AFMR进行坐标转换,文献[16]在信噪比-6 dB下的识别率也远超另外两种方法,表明用AFMR进行信号的分选识别是行之有效的;文献[17]因为使用了主成分分析和随机投影对信号进行降维,在此过程当中损失的信息较多,所以识别率较低;文献[18]仅仅改变了分类器,对提高识别率没有太大效果。由此可见,本文所采取的模型有更好的泛化能力和抗噪性,本文方法是可行和有效的。
3.4 不同输入形式性能对比
通过对AFMR和其他信号输入形式进行对比,旨在探究AFMR极坐标变换的实用性。选取文献[6]和文献[8]进行对比,结果如图9所示。

图9 不同输入形式对比Fig.9 Comparison of different input forms
由图9可见,3种输入形式在信噪比0 dB以上都有90%以上的准确率,而在低信噪比环境下的表现却不尽相同。除本文方法外,其余两种输入的识别率都不尽如人意,特别是文献[6]在信噪比-6 dB时的识别率仅在70%左右。这是因为文献[6]的输入形式为CWD提取的信号时频特征图,在低信噪比下信号几乎失真,提取到的时频图信息不完备,故抗噪性能较差。文献[8]的输入则是信号双谱图,由于是在傅里叶变换的相位中提取信息,在低信噪比下双谱信息不足以支持信号的识别。而本文方法在低信噪比下的表现依旧令人满意,信噪比-6 dB时的识别率在90%以上,可见本文方法的实用性。
3.5 不同算法性能对比
为进一步探究一维AF主脊图经过极坐标变换成二维时频图后识别性能的增益,构造一维AF主脊数据集分别作为栈式自编码机(SAE)、深度信念网络(DBN)和一维CNN的输入进行测试,对比结果如表4所示。
由表4可知,本文采取的二维AFMR+CNN在不同信噪比下的识别精度和平均用时上都远高于另外3种算法,表明从AFMR的极坐标图像入手是切实可行的。这是因为6类RES的一维AFMR在低信噪比下严重交叠,已经完全分辨不出信号的具体类型,而经过极坐标变换后的二维AFMR图比极坐标变换前的AFMR曲线更加形象直观,凸显了一维AFMR的细微差别,不同信号间的极坐标图像有着明显差异,且信号经过极坐标转换后信息没有受到损耗。其次,通过采用CNN的1组、4组与2组、3组对比可知,在不考虑输入的前提下,CNN在分类问题中的表现要优于其他神经网络,这是因为CNN提取到的特征都是较高质量的特征,能够提升网络识别率,同时CNN在图像处理领域有着得天独厚的优势,能够捕获图像更复杂、更抽象的信息。而SAE和DBN对输入数据的平移不变性有很高的要求,生成模型DBN不关心不同类别之间的最优分类面的划分,所以用于分类时精度不高。另外3种方法在一次Epoch所需时间上均为本文算法的1.5倍左右,而DL又是需要进行多个Epoch学习的过程,由此可知本文算法大大加快了模型的计算速度。因此本文算法能够有效弥补其余算法精度低、训练难度大等不足,进而可以得到相对更为科学的实验结果。
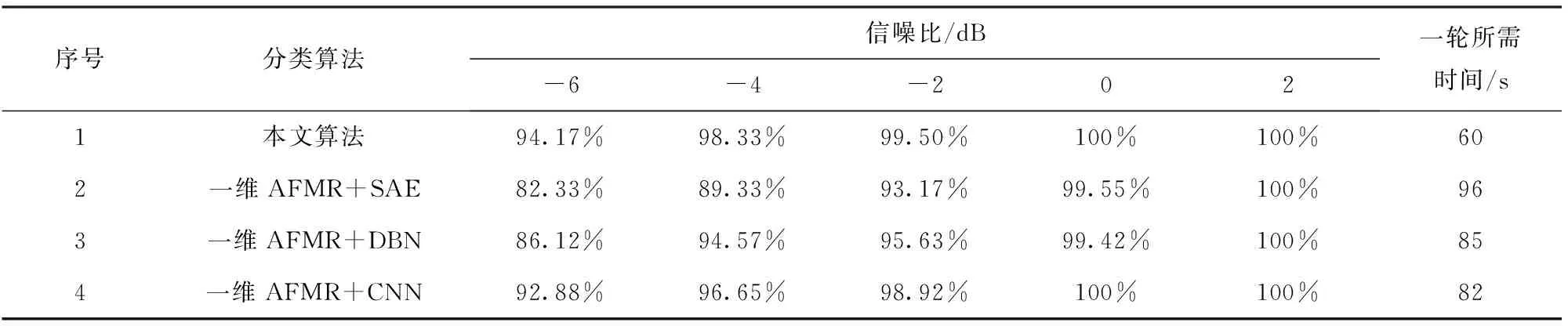
表4 不同分类算法训练情况(识别率)Tab.4 Training of different classification algorithms (recognition rate)
3.6 实测雷达数据实验
为了进一步验证本文在实际战场中的应用价值,采用某外场RES实测数据进行实验,该辐射源信号与本文6类仿真RES脉内调制情况一致。实测数据具体参数如表5所示。将实测数据输入到已经调试好的CNN网络当中,信号的识别结果如表6所示。

表5 实测雷达数据参数Tab.5 Measured radar data parameters

表6 实测数据分选结果Tab.6 Sorting results of measured data %
从表5中可以看出,实测数据当中的调制类型都不相同,而且RF和PW还存在抖动和捷变,完全符合实际战场中复杂的电磁环境要求。即便如此,本文方法对实测数据的识别率仍然能达到93.2%,由此可见本文方法在复杂多变的电磁环境中仍然具有一定的工程意义,基本满足实际战场的需要。
3.7 算法复杂度分析
算法复杂度体现在执行该算法时所经历的资源消耗上,不同算法所需的资源消耗也不尽相同,体现了各类算法计算量的差异,因此可从信号重采样长度N和计算规模的角度出发,分别对极坐标转换前后的AFMR以及文献[15]的计算量进行分析。本文二维AFMR的提取:首先,利用分数自相关计算任意角度对应的AF值,一次分数自相关运算包含一个1+P阶(P为分数域阶数)的分数傅里叶变换和一次分数傅里叶逆变换;其次,需要在[-π/2 rad,π/2 rad]范围内对AFMR进行搜索,搜索精度为0.1°时搜索次数为1 800次。因此一维AFMR的复杂度为O(18 000NlgN),而经过极坐标变换后的二维AFMR的复杂度为O(7N+18 000NlgN)。文献[15]采用CWD变换作为分形维数的提取对象,其次采用复杂度为O(N3)的奇异值分解进行矩阵相乘运算,频谱和CWD变换采用快速傅里叶变换实现,所以该文特征算法复杂度为O(N3+2N+2NlgN)。
综上所述,当信号的采样长度较长时,二维AFMR的复杂度稍大于一维AFMR,却要小于分形维数方法。然而,当信号的采样长度较短时,文献[15]的算法复杂度最低,其次是一维AFMR,但是二者在低信噪比下识别率较低,并且本文为了AFMR的搜索精度采用穷举法,大幅度增加了算法复杂度。因此,本文算法复杂度虽然略高,但是保证了搜索精度和实验结果的高准确性。
4 结论
为克服人工特征提取方法耗时长,对专家知识储备要求高等问题,本文基于DL能提取信号隐藏抽象特征的优势,提出了一种AFMR极坐标变换和CNN的RES识别方法。通过仿真实验结果分析,得出如下主要结论:
1)本文方法识别率高、抗噪性较强,在信噪比0 dB以上都为100%,即使在信噪比-6 dB时也有90%以上的识别率。
2)与AF各类处理方法相比,AFMR极坐标变换不损耗特征信息,能较好地反映信号间差异,增加了信息的利用率,有助于神经网络提取更加优异的特征。仿真实验和实测数据均表明所提方法具有较强的时效性。
本文实验仅仅在6类RES中进行,对模型的普适性还需要进行下一步的分析研究,而且DL需要先验信息,但在实际战场当中大部分都是未知的雷达信号,如何对未知信号构建有效分选参数集以及对CNN进行结构上的优化,是下一步需要研究的方向。

