针对弹载卫星导航接收机干扰方向测定的算法研究

赵怡萌，付晶晶，童 栎，庄树峰，刘 路

(1. 北京自动化控制设备研究所，北京 100074;2. 陆军装备部航空军事代表局驻北京地区航空军事代表室，北京 100012)

0 引言

在日益激烈的电子对抗中，弹载卫星导航接收机接收的卫星信号十分微弱，极易受到电磁干扰。目前，通常使用自适应空时滤波技术[1]，设计自适应抗干扰天线在干扰方向上自适应产生零陷[2]，从而达到抑制干扰的目的。自适应算法的权值是根据一段时间的信号样本计算得到的，而大动态的弹载卫星导航接收机相对干扰源的方位变化较快，造成自适应算法形成的零陷深度变浅、范围变大，进而导致接收机的抗干扰能力下降，同时影响干扰方向附近卫星信号的接收。特别是在面对突发干扰时，零陷指向会出现偏差。为此，采用波达方向(Direction of Arrival，DOA)估计技术解决干扰方向与零陷方向延迟的问题已经成为当前弹载卫星导航接收机抗干扰领域的发展趋势[3-5]。经典的子空间DOA有2个具有代表性的算法：多重信号分类(Multiple Signal Classification，MUSIC)[6]算法和旋转不变子空间(Estimating of Signal Parameters via Rotational Invariance Technique，ESPRIT)[7]算法。MUSIC算法分辨率高，但计算量大，运算速度慢[8]，不适用于高速弹载卫星导航接收机干扰方向的测定。ESPRIT算法无需谱峰搜索，计算速度快[9]，但在多干扰时，部分干扰来向的测定结果存在固定偏差，且测定精度随着干噪比降低而下降。

本文首先建立了用于DOA估计的系统模型，分析了常用的干扰测向算法,针对MUSIC算法计算量大和ESPRIT算法测定精度低的问题，提出并详细阐述了MUSIC-ESPRIT联合算法的设计原理和实现步骤。最后，将MUSIC-ESPRIT联合算法与其他干扰测向方法进行了仿真分析对比，并给出分析结果。

1 DOA估计系统模型

1.1 天线阵列接收的信号模型

假设天线阵列由M个阵元组成，则接收信号的矢量可表示为

X=ASS+AJJ+N

(1)

式中

X=[x1,x2,…,xM]T,xi(i=1,2,…,M)
S=[s1,s2,…,sq]T,si(i=1,2,…,q)
J=[j1,j2,…,jp]T,ji(i=1,2,…,p)
N=[n1,n2,…,nM]T,ni(i=1,2,…,M)
AS=[α1,α2,…,αq]M×q
AJ=[β1,β2,…,βp]M×p

(2)

X为接收信号的列向量，xi代表第i个阵元接收到的信号；S为q个卫星信号的列向量，si代表第i个卫星信号；J为p个干扰的列向量，ji代表第i个干扰；N为噪声的向量，ni代表第i个阵元的噪声，为零均值，方差σ2的高斯分布,这些噪声彼此独立，并且与卫星信号和干扰无关;AS为卫星信号的导向矢量阵;AJ为干扰信号的导向矢量阵。式中

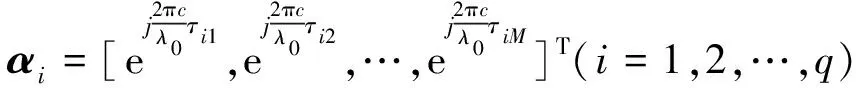
(3)

αi为卫星信号si(t)的导向矢量；βi为干扰ji(t)的导向矢量;τim(m=1,2,…,M)为卫星信号或干扰从发射端到达第m个阵元的时间延迟；c为光速；λ0为卫星信号的波长。

1.2 均匀圆形天线阵列接收的时间延迟

由1.1节的公式可知，只要知道每个阵元接收每个卫星信号和干扰的时间延迟τ的具体表达式，就可以得出阵列的导向矢量。以圆形阵列天线为例，先讨论2个阵元的情况，设其中一个为参考阵元即此阵元位于直角坐标系的原点，另一个阵元的坐标设为(x,y,z)，当信号的入射方向为(θ,φ)时[10]，则可知时间延迟为

(4)

进而可知，当以均匀圆阵的圆心为参考点，M个阵元以r为圆阵半径时，时间延迟便为

(5)

至此，圆形天线阵列的信号接收模型构建完成。

2 干扰测向算法

干扰测向将阵列天线接收信号中超过噪声功率的信号方向定为干扰方向[11]，其测定的结果可通过基于线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)准则的波束形成算法[12]应用于弹载卫星导航接收机抗干扰模块中。目前存在的多种测定干扰方向的算法中，最具有代表性的便是子空间算法。其中，MUSIC算法测定精度高，但需要进行全方位的谱峰搜索，增加了计算复杂度，这也是MUSIC算法不能直接用于弹载卫星导航接收机测向的主要原因。ESPRIT算法无需空间谱搜索，运算量小，但精度低，且干扰个数越多精度越低。

2.1 MUSIC算法

MUSIC代表多重信号分类法，是最早的超分辨DOA估计方法，其原理是利用干扰子空间和噪声子空间的正交性，构造空间谱函数，通过谱峰搜索测定干扰的来向。

其中，阵列数据协方差矩阵R可以写为

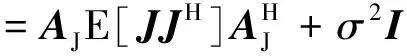
(6)

式中，RJ为干扰信号的协方差矩阵。

2.2 ESPRIT算法

ESPRIT算法采用基于相位模式激励的波束空间变换处理算法[13]，通过波束形成矩阵将阵列从阵元空间变换到波束空间。利用波束空间阵列导向矢量的分解和贝塞尔函数的递推关系得到矩阵方程，对该矩阵方程的最小二乘解再进行特征分解，即可得到干扰的方位角和俯仰角[14]。ESPRIT算法得到的是解析解，且方位角和俯仰角成对出现，计算较为简单，在二维的 DOA 估计中具有很高的实用价值。

3 MUSIC-ESPRIT联合算法

由于MUSIC算法的运算量大，而ESPRIT算法的精度不足且多干扰时存在偏差，为了克服二者的缺点同时发挥各自的优点，本文提出了MUSIC-ESPRIT联合算法。

计算波束形成矩阵Fr

(7)

其中

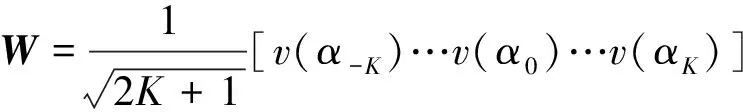
(8)

式中，K为均匀圆阵能够激励的最大相位模式数，wi(i=-K,…,K)为波束形成加权矢量。由此，空间波束输出的协方差矩阵可以表示为

(9)

取协方差矩阵Ry实数部分做特征值分解，将得到的特征向量按照特征值λ1≥λ2≥,…,≥λ2K+1>0进行排序，对应前p个特征向量构成干扰子空间J。计算干扰矩阵J0为

J0=C0J

(10)

其中

C0=diag{(-1)K,…,(-1)1,1,11,…,1K}

(11)

分区获取矩阵J(i)

J(i)=Δ(i)J0

(12)

式中，i=-1,0,1。选择矩阵分别取行数为2K-1的3个矩阵J(-1)、J(0)和J(1)。

构造矩阵

E=[J(-1)J(1)]

(13)

求解公式

(14)

式中

(15)

根据最小二乘法求得

(16)

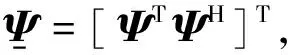
θi=cos-1(|μi|)
φi=arg(μi)

(17)

计算R的特征值，满足

(18)

将M-p个特征值为σ2对应的特征向量构成M×(M-p)维的噪声空间VN为

VN=[vp+1,vp+2,…,vM]

(19)

空间谱函数为

(20)

本文提出的MUSIC-ESPRIT联合算法的流程图如图1所示。MUSIC-ESPRIT联合算法的具体实现步骤如下：

步骤1：通过功率统计模块，判断输入信号的功率，同时计算输入信号的自相关矩阵;

步骤2：根据功率统计的结果确定MUSIC算法的搜索范围，同时计算噪声子空间，并计算出ESPRIT算法的测量值;

步骤3：将ESPRIT算法的测量结果作为初始值，进行限定范围内的谱峰搜索;

步骤4：峰值对应的方向作为最终值输出。

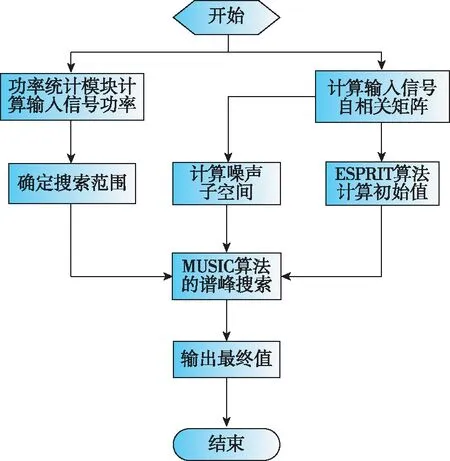
图1 MUSIC-ESPRIT联合算法流程图Fig.1 Flow chart of MUSIC-ESPRIT joint algorithm

本文提出的MUSIC-ESPRIT联合算法将ESPRIT算法的测定结果作为初始值，缩小了谱峰搜索的范围，降低了干扰测向的运算量。

4 仿真验证

为了比较MUSIC-ESPRIT联合算法与传统的MUSIC算法和ESPRIT算法的测向性能，通过仿真实验，对比分析了三种算法的干扰测向性能。选取七阵元的均匀圆阵，为减小阵元通道间互耦的影响，圆阵半径为干扰信号的半波长,同时考虑计算时间不宜过长，快拍数设为128。为了检验它们在不同干噪比下对干扰方向的测定结果，将干噪比分别设为10dB和50dB。

4.1 干噪比为10dB下干扰方向的测定

假设为双干扰情景，干扰入射方向用坐标形式表示，即(方向角，俯仰角)，干扰1 的入射方向为(120°，30°)，干扰2 的入射方向为(240°，60°)，干噪比为10dB。

MUSIC算法对干扰方向的测定结果如图2所示。为形象说明ESPRIT算法对干扰方向的测定结果，在不同干噪比的条件下分别进行3000次独立的蒙特卡罗仿真，干噪比对干扰测向精度的影响如图3所示。MUSIC-ESPRIT联合算法的测定结果如图4所示。三种算法的处理时长见表1。

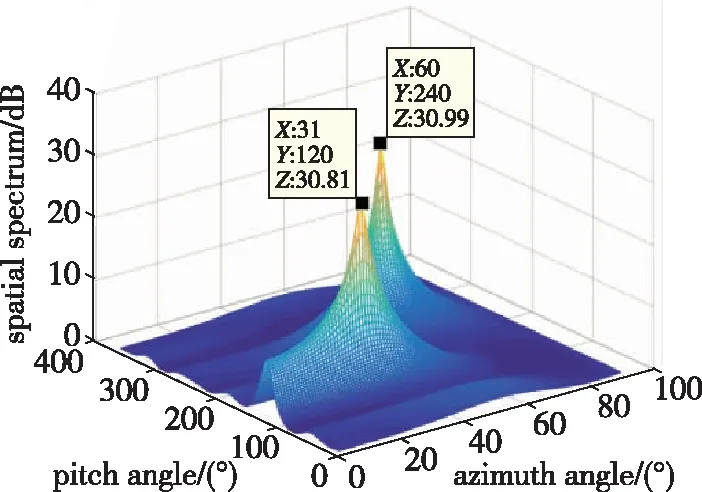
图2 MUSIC算法干扰测向结果(干噪比为10dB)Fig.2 Jamming direction finding results of MUSIC algorithm(I/N=10dB)

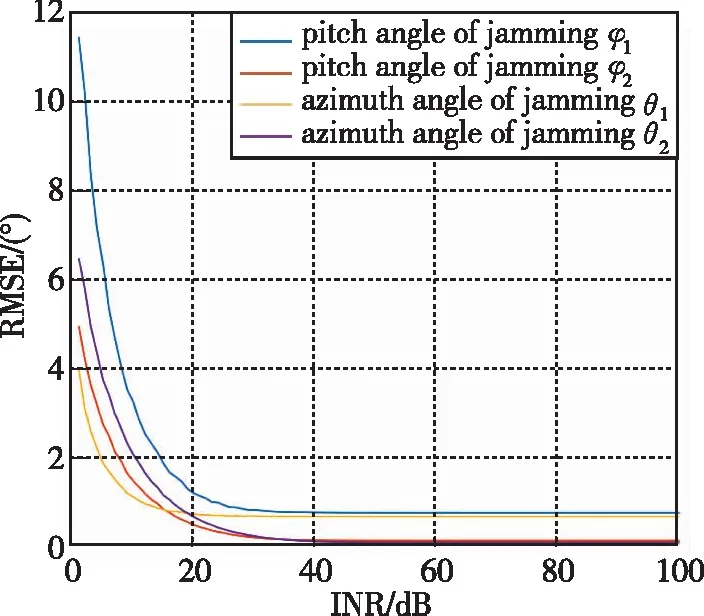
图3 ESPRIT算法干扰测向结果Fig.3 Jamming direction finding results of ESPRIT algorithm

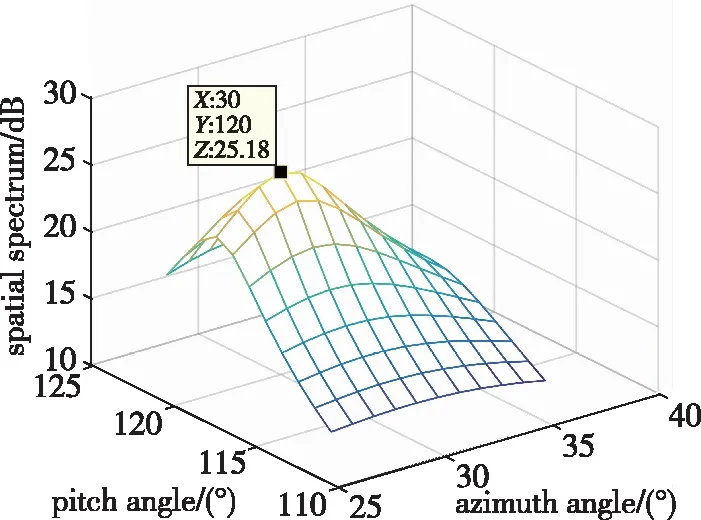
(a)干扰1的来向

由表1对比MUSIC算法与本文提出的MUSIC-ESPRIT联合算法的运算时长可以发现，本文提出的MUSIC-ESPRIT联合算法可以将运算时长降低1个量级。而从图2和图4可以看出，本文提出的MUSIC-ESPRIT联合算法对干扰方向的测定精度与传统的MUSIC算法的测向精度都可以精确到1°以内，同时满足了高动态应用条件下对干扰测向实时性和高精度的要求。

表1 三种算法的运算仿真时长

从图3仿真结果可以看出，ESPRIT算法测量精度随着干噪比的增大而提高，在干噪比接近0dB时，测出的方向角的最小误差为4°，最大甚至大于10°，故而在干噪比较低时，需要较大范围的谱峰搜索。随着干噪比的增大，测量精度有所提升，但有一个干扰的测定结果存在固定偏差。为此本文提出的MUSIC-ESPRIT联合算法需要根据输入信号的功率调整谱峰搜索范围，以保证干扰测向的精度。

4.2 干噪比为50dB下干扰方向的测定

干扰入射方向不变，将干噪比提高至50dB，其中MUSIC算法的干扰测向结果如图5所示，本文提出的MUSIC-ESPRIT联合算法对干扰方向的测定结果如图6所示。

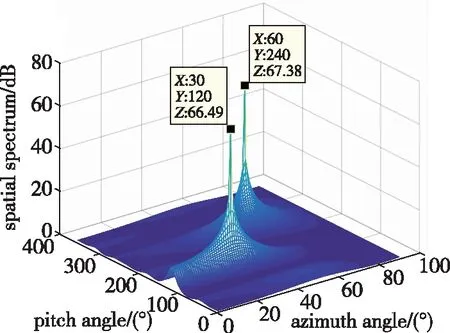
图5 MUSIC算法干扰测向结果(干噪比为50dB)Fig.5 Jamming direction finding results of MUSIC algorithm(I/N=50dB)

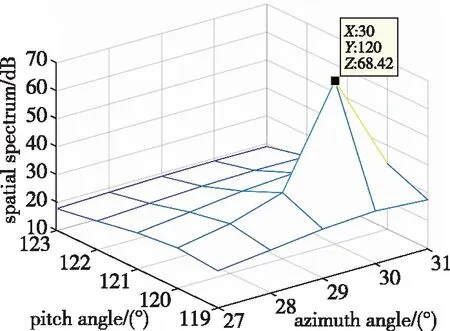
(a)干扰1的来向

针对随着干噪比增大ESPRIT算法测向误差减小的规律和固定偏差的问题，本文提出的MUSIC-ESPRIT联合算法通过较小范围的谱峰搜索，在进一步减少计算量的同时保证对干扰来向的测定精度。从仿真结果图5与图6可以看出，在干噪比为50dB的情况下，两者的测量精度在同一量级。

5 结论

针对弹载高动态卫星导航接收机干扰方向的测定问题，本文提出了MUSIC-ESPRIT联合算法。算法分析与仿真实验结果表明：

1)与传统的MUSIC算法相比，降低了干扰方向测定运算的复杂度。

2)低干噪比时，MUSIC-ESPRIT联合算法与传统的ESPRIT算法相比，提高了干扰方向的测定精度；高干噪比时，不存在多干扰测定产生的固定偏差。

3)进一步提高处理速度，是后续实现弹载卫星导航接收机对干扰方向实时测定的关键。