基于状态改变的机器人路径规划算法

陈麒杰，晋玉强，王陶昱

(海军航空大学岸防兵学院，烟台 264000)

0 引言

随着科学技术的不断进步和制造工艺的提高，机器人在军事[1]、运输[2]、救援[3]、商业、娱乐和农业[4]等领域的应用越来越广泛。机器人在执行任务过程中，合理的规划路径是实现有效避障和快速到达目标点的基本要求，也是高效完成任务的前提条件。因此，对于机器人的路径规划研究越来越成为目前研究的热点之一。

目前，机器人路径规划算法主要有以A*算法[5]、路线图法[6]、细胞分解法[7]和人工势场法[8]为代表的经典路径规划算法，以及以遗传算法[9]、粒子群算法[10]、蜂群算法[11]和布谷鸟算法[12]为代表的智能路径规划算法。经典算法在面对多障碍物、规划面积较大时，其计算量显著增加，解算速度明显降低，导致时效性降低；智能规划算法对于任务规划区域的信息获取度要求高，并需要多次学习和模拟，很难实现在未知环境中的路径规划，降低了路径规划的使用范围，减小了能够使用智能算法的任务区域。而人工势场法作为一种简单高效的经典路径规划方法，得到了广泛的研究与应用。文献[13]中将人工势场法改进后应用于机器人的路径规划，该方法的优点是在提高时效性的同时，有效降低了路径规划的难度。文献[14]中通过建立动态调节因子改进人工势场法中的斥力场，实现无人机逃离极小值点，从而到达预定目标，但需要计算的候选路径多，降低了时效性和全局性。文献[15]中利用流函数法对人工势场进行拓展，利用沿墙随机行走和改变目标引力的方法避免滞点和目标不可达问题，但该算法在设置虚拟障碍物时，需要预先获得区域内的障碍物信息，降低了实时性。文献[16]中利用神经网络的自学能力改进人工势场法的系数选择，以实现逃离局部极小值，但该方法的准确程度依赖于样本的数量和训练次数，对于样本较少、学习量低的规划区域，很难计算出有效的自适应系数，导致避障失败。文献[8]中利用搜索算法改进人工势场法，以避免无人机陷入极小值点，但在算法运算过程中，需要对极小值点内的障碍物进行全局搜索，降低了算法的时效性。

本文针对上述问题，参考电路中理想电感元件能够在直流电压变化后，由感抗状态恢复到稳定状态的现象，提出了一种基于状态改变的机器人路径规划算法。以机器人速度和方向为基础，建立机器人状态改变检测量，利用克罗内克函数实现对机器人速度状态在不同时刻的对比，确定避障时机和避障策略，从而实现机器人避障，最终到达目标点。仿真结果表明，该方法能够成功有效地实现机器人的自主避障，同时规划出符合条件设定的路径。

1 基于状态改变的路径规划算法基础

设机器人所在平面为xoy平面，空间中任一点的向量可以表示为P=(x,y)，无人机器人起始点的向量为P0=(x0,y0)，在任意时刻的位置为Pt=(xt,yt)，目标点位置向量为Pg=(xg,yg)。

本文中为了简化模型条件，对机器人和障碍物作出如下假设：

1)平面内障碍物根据其最大半径，膨胀为圆形障碍物，则圆形障碍物模型可表示为

(1)

其中，Pobsn=(xobsn,yobsn)为第n个障碍物中心点向量；rn为障碍物半径。

2)机器人运动时，可以实时获得当前时刻的位置、速度和速度方向。

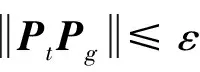
4)假设机器人的质量为1，直径为dU，行进速度为固定的巡航速度VR，且满足VR≤Vmax，其中Vmax为机器性能决定的最大巡航速度。

2 基于状态改变的二维路径规划

在二维平面中，将机器人向目标点行进作为系统的稳定状态，每一个障碍物作用的叠加则是对该稳定状态改变的激励状态。类比电路中理想电感元件在电源电压发生改变后，当电源电压稳定时，电感元件两端电压能够从感抗状态恢复到初始状态的现象。因此，提出了基于状态改变的二维路径规划算法。

假设机器人在场内任意一点受到向量场的作用向目标点前进，得到机器人在任意一点由该点向目标点的方向向量，即机器人初始的稳定状态为

(2)

当平面场内没有障碍物时，机器人将沿着由起点到终点的直线向量场前进，根据机器人本身的性能确定速度。

当平面内存在障碍物时，机器人为了尽快恢复到初始的运动状态，会选择路径较短的方向，沿着障碍物边缘的切线与目标点方向夹角小于90°的方向，通过改变机器人的前进方向，达到避障的目的。由机器人和障碍物中心所在点可得障碍物方向向量为

(3)

根据式(3)得障碍物切向量为

(4)

引入克罗内克函数[17]，该函数满足

(5)

根据式(2)、式(4)和式(5)可得单个障碍物对机器人的作用力为

Fobsn=

(6)

对于多障碍物存在的行进平面内，定义第n个障碍物的影响系数为

(7)

根据式(7)可以确定，通过改变障碍物作用半径，可以改变机器人避障时机，确保机器人的避障成功。根据式(6)和式(7)可得N个障碍物对机器人的作用合力为

(8)

则机器人的加速度变化量为

(9)

定义t时刻机器人的速度向量为

(10)

根据式(2)和式(9)可得机器人在障碍物作用下的中间变化向量为

VR+aobsN·Δt

(11)

根据机器人性能得最大转角为α，定义矩阵T为机器以最大转角逆时针转向的旋转矩阵

(12)

由式(12)可得，矩阵T作用时，机器人将按照最大转角逆时针旋转。

综上可得，机器人在t+1时刻的速度方程为

vuavt+1=(vF+vuavt·δ(〈vF,vuavt〉)·

(13)

通过对速度量的积分，可以得到机器人的下一个路径点为

Pt+1=Pt+vuavt+1·Δt

(14)

式中，Δt为计算步长。通过迭代得到每一个步长下的位置点，将每一个路径点相连，可以得到机器人前进的最终路径。

3 避障分析

3.1 单个障碍物避障分析

单个障碍物时，选取圆形障碍物的圆心位置为Pobs=(a,b)，半径为r，斥力作用半径为R，单个障碍物模型可化为

Γ：(x-a)2+(y-b)2=r2

(15)

根据式(13)可得，机器人运动分为2个状态，即直线运动状态和避障状态。

设机器人当前坐标为Pt=(xt,yt)，则直线前进阶段

(16)

当机器人首次进入障碍物作用范围内时，其路径规划方程为

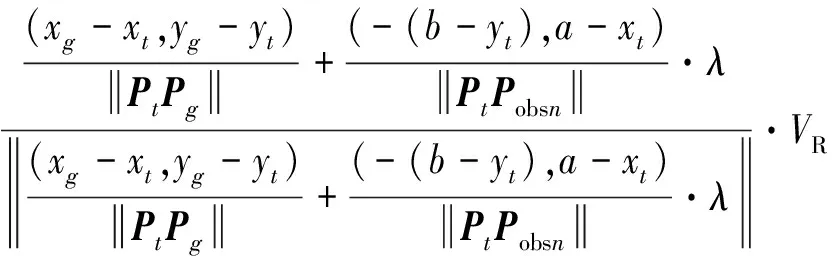
(17)

机器人在结束初次进入障碍物作用范围的运动后，其运动方程为

(18)

机器人避障成功，脱离避障区域后，其运动方程为

(19)

由以上公式可得，机器人在避障前后的状态没有改变，只有当进入到避障区域内，受到障碍物影响，状态发生改变的情况下，按照避障策略实现避障。

3.2 目标不可达问题改进

针对目标不可达问题，对避障过程中的障碍物系数添加角度和障碍物间距的判定条件，对不满足条件的障碍物，其作用系数为0 ，根据式(1)可得，在考虑机器人直径的情况下，障碍物方程可以等效为

Γ(P)：(x-xobsn)2+(y-yobsn)2=(rn+dU)2

(20)

增加判定条件Q

(21)

根据式(7)和式(21)可得,改进后的障碍物作用系数为

(22)

根据式(22)，当目标点附近存在障碍物时，机器人进入障碍物作用区域后，该障碍物作用系数为0，因此机器人能够有效到达目标点。

3.3 滞点问题改进应对策略

利用机器人对障碍物之间距离的实时检测，将滞点问题分两种情况讨论。

情况一：障碍物间距小于机器人直径的情况

当机器人运行至对称障碍物时，因为相同障碍物系数的作用，使得机器人避障失败(如图1所示)。

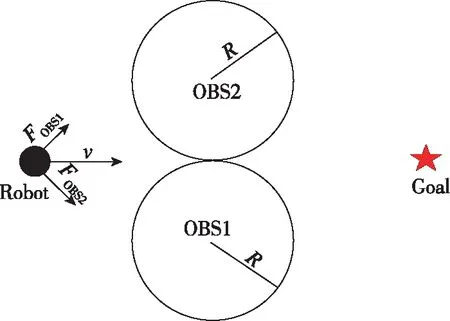
图1 极小值点示意图(情况一)Fig.1 Schematic diagram of minimum point (Case 1)

当机器人运行至图1所示位置时，障碍物产生的作用向量可由式(9)和式(13)计算得到

vuavt=

(23)

根据式(23)可得，当障碍物间距小于机器人直径时，机器人将按照最大转角实现避障。

情况二：障碍物间距大于机器人直径的情况

当障碍物间距大于机器人直径时(如图2所示)，引入作用向量为0的条件，可以实现快速路径规划，以较少的路径点到达目标点，避免陷入陷阱。

图2 极小值点示意图(情况二)Fig.2 Schematic diagram of minimum point (Case 2)

4 数值仿真

根据以上理论推导，在本算法中，主要是对机器人的状态进行检测，包括速度的方向和大小，根据其速度相较于初始状态的不同，得到算法中下一步的执行状态。算法的流程图如图3所示。

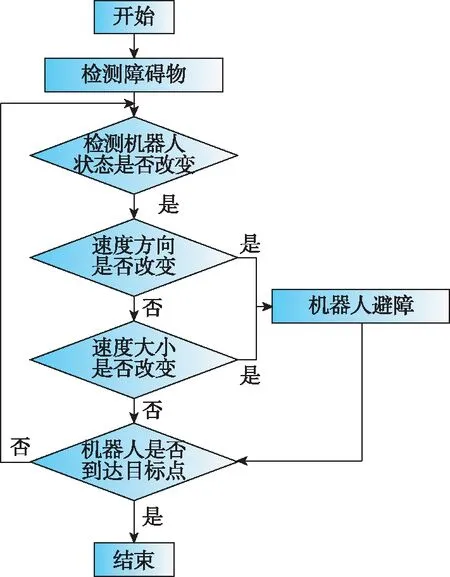
图3 基于状态改变的机器人路径规划算法流程图Fig.3 Flow chart of robot path planning algorithm based on state change

4.1 仿真环境构建

利用MATLAB按照以上流程针对不同情况对算法进行仿真，仿真条件如表1所示。

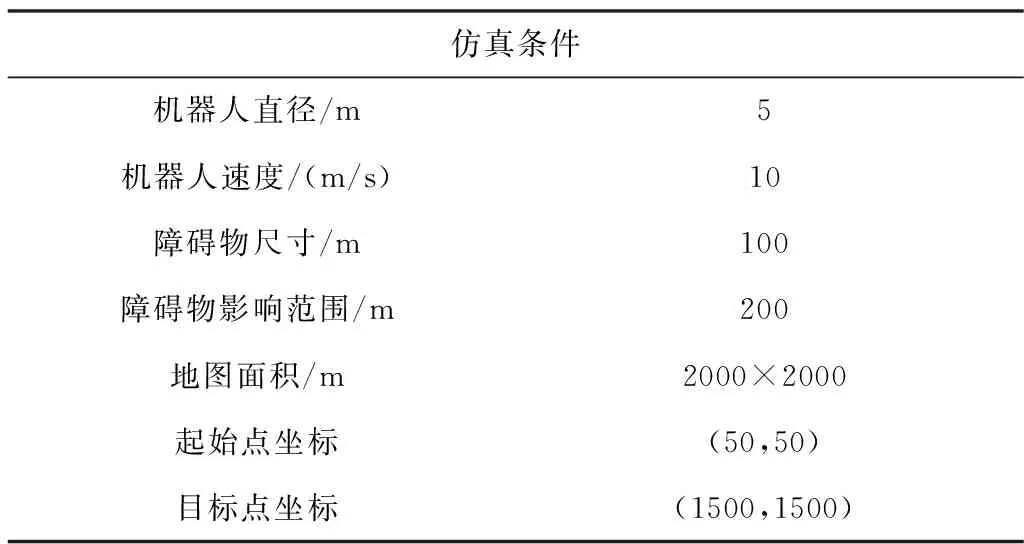
表1 仿真条件

4.2 仿真结果分析

当传统人工势场法遇到滞点时，如图4和图5所示，轨迹点会在障碍物附近徘徊，直到耗尽设定的最大步数为止；当目标点附近存在障碍物时,如图6所示，机器人会在目标点附近徘徊，直到走完所有的规划步数，不能到达目标点。

图4 人工势场法仿真图(情况一)Fig.4 Simulation diagram of artificial potential field method (Case 1)

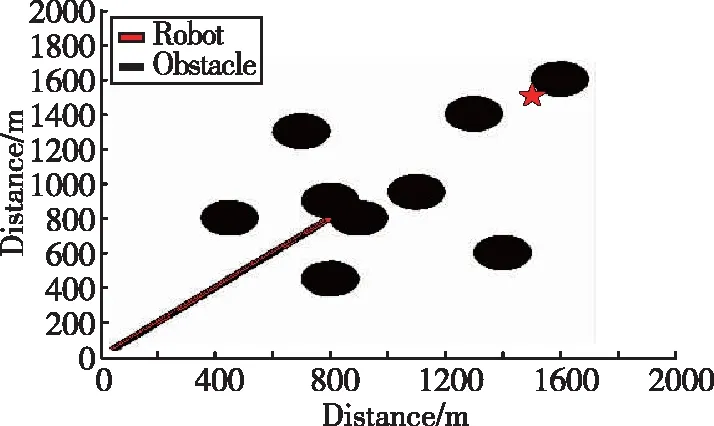
图5 人工势场法仿真图(情况二)Fig.5 Simulation diagram of artificial potential field method (Case 2)

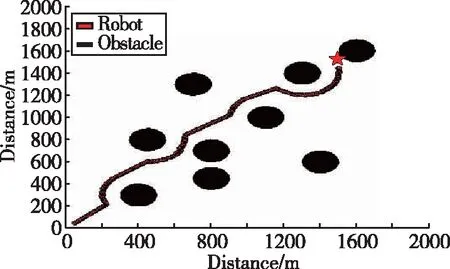
图6 人工势场法仿真图(目标不可达)Fig.6 Simulation diagram of artificial potential field method (Target unreachable)

相同环境下，采用本文算法进行规划，针对以上问题，均成功规划出一条合理的路径轨迹，如图7和图8所示。

图7 基于状态改变的路径规划算法仿真图(情况一)Fig.7 Simulation diagram of path planning algorithm based on state change (Case 1)

图8 基于状态改变的路径规划算法仿真图(情况二)Fig.8 Simulation diagram of path planning algorithm based on state change (Case 2)

由图7和图8可以看出，机器人能够避免人工势场法中的极小值点，并且能够按照不同情况实现避障。当障碍物间距小于机器人直径时，机器人按照最大转角实现避障；当障碍物间距大于机器人直径时，从障碍物中间穿过，以降低路径规划计算量；在目标点附近存在障碍物时，不受障碍物影响，能够到达目标点。

5 结论

本文借鉴电场出现外界激励后恢复到稳定状态的现象，提出了一种基于状态改变的机器人二维路径规划算法，主要完成以下工作：

1)引入机器人状态检测中间量，实现机器人避障时机和避障策略的选择；

2)引入障碍物作用条件，当满足障碍物作用条件时，机器人状态受到障碍物影响，避免人工势场法中的极小值点以及目标不可达问题；

3)引入克罗内克函数，实现对最大转角矩阵作用条件的判断，避免障碍物间距小于机器人直径时产生极小值点；

4)文中图7和图8的路径规划时间分别为23.76s和16.57s，路径长度分别为3527.334m和2918.546m，最大转角分别为75°和43°。从时间上看，本文算法能够保证路径规划的时效性；从路径长度和最大转角看，本文算法不能够保证得到的规划路径是最优路径，并且没有充分考虑机器人实际的物理性能。

通过虚拟环境的仿真实验，验证了本文算法的有效性和优越性。为下一步移动障碍物避障和路径规划研究，以及移动机器人平台上的实际应用奠定了理论基础。下一步的工作将进一步对算法进行研究，拓展算法适用的避障条件，以及对算法规划路径的平滑，降低对机器人本身条件的约束。