混合动力汽车行星齿轮式耦合器设计

刘子萌，谢建新

（青岛黄海学院，山东 青岛 266427）

前言

行星齿轮机构具有结构紧凑简单、质量轻、承载能力强等优点，其在运行过程中可以改变动力传递路线，同时可以进行多种运动组合实现多种传动比，其运行工况稳定，并且抵抗冲击能力强，所以混合动力汽车通常使用行星齿轮作为其传动系统。

1 行星齿轮设计

混合动力汽车采用的行星齿轮传动系统一般是一个两自由度单排差动行星齿轮机构，输入件为发动机，输出件分别与电动机/发电机相连，主要用于驱动车辆行驶。发电机并不是动力源而是实现调速，进行能量分流[1]。

混合动力汽车行星齿轮机构主要有五个部分组成：行星架、太阳轮、行星齿轮（一般由1～3个组成）、齿圈、固定杆。五个部分组成回转轮系，包含六个运动副分别是四个转动副、两个移动副。一般情况下输入件为太阳轮或是行星架，输出件是齿圈。行星齿轮机构中全部齿轮均为标准直齿圆柱齿轮并且有两个自由度[2]。

发动机、发电机、电动机/发电机三者与行星齿轮机构相连接的方式比较多，一般有六种情况，进过实验对比发现发动机与行星架相连接，电动机/发电机与内齿圈相连接，发电机与太阳轮相连接的连接方式具有传动效率高，速比分配合理，对发动机、电动机、蓄电池等使用性能要求低等优点[3]。普遍应用于混合动力轿车。在此中连接方式中进行行星齿轮机构的设计，其中发动机与行星架通过离合器相连接，电动机/发电机与齿圈直接连接，发电机与太阳轮通过一对减速齿轮相连接，锁止功能通过制动器完成将发电机锁止。

2 行星齿轮有限元分析

行星齿轮机构在传递扭矩过程中，齿与齿通过面接触和线接触完成力矩传递，长时间运行齿面发生磨损甚至是折断，齿轮传动失效，导致耦合器失效。在进行行星齿轮机构设计过程中需要对其进行静力学分析以验证其强度和刚度是否满足设计要求。行星齿轮机构在工作过程中除了传递力矩还受到冲击载荷作用，载荷是周期性的变化，甚至会产生比较强烈的振动，从而导致齿轮机构整体产生疲劳损失，所以需要对行星齿轮机构进行模态分析验证其设计在其工作各种工况下时都会产生共振现象[4]。

2.1 模型建立

在solidworks三维建模软件总输入所设计行星齿轮机构的各个零部件参数，建立行星齿轮中各个零部件的模型，然后将各个零部件按照一定的规则进行转配，建立行星齿轮机构模型。

2.2 静力学分析

2.2.1 强度分析

将所建模型导入ANSYS仿真软件中，运用ANSYS软件中Workbench模块对模型施加载荷进行强度分析，得到应力云图如图1所示。由图可知行星齿轮机构最大应力为301.46 MPa，最大应力处于行星齿轮与齿圈、行星齿轮与太阳轮啮合的位置，属于正常的受力位置。行星齿轮机构所选材料的屈服强度为835 MPa，最大应力301.46 MPa小于屈服强度符合设计要求，而且应力分布均匀，也符合行星齿轮载荷均衡的特点。

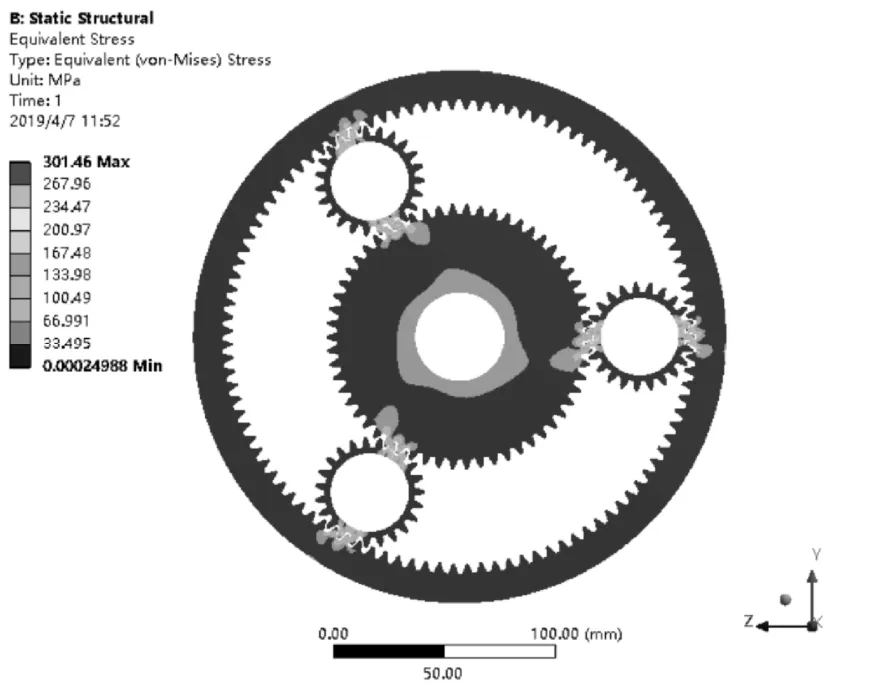
图1 行星齿轮耦合器应力云图

2.2.2 刚度分析

刚度是衡量刚性物体受力抵抗变形的能力，行星齿轮在进行力矩传递过程中，如果传递再和大于其刚度会发生弯曲变形从而发生失效，验证其刚度是非常有必要的。导入仿真软件模型施加载荷得到云图如图2所示。从图可知行星齿轮机构最大变形量为0.008 5 mm，变形出现在齿圈与两个行星齿轮相啮合的外圆周侧，而且最大变形量在外侧中间位置，符合齿圈正常运行状态，最大变形量非常小，对与齿圈的正常运行不会产生影响，可以忽略不计。

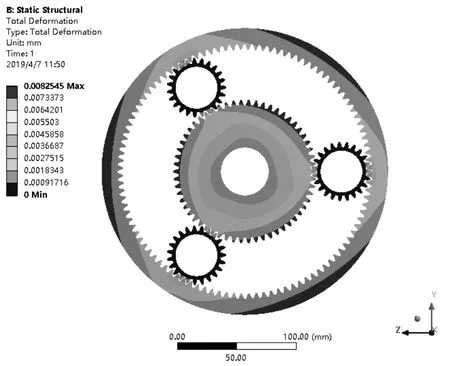
图2 行星齿轮耦合器变形云图

2.3 模态分析

为了研究行星齿轮耦合器运转时是否会发生共振的问题，需要计算行星轮系的固有频率，针对仅电机工作，发动机/电机同时工作，电磁锁死控制单元起作用三种工作状态，分别进行模态分析。一般来说，引起行星齿轮共振的主要是低阶次频率。因此，利用ANSYS中的Block Lanczos法提取了前6阶模态频率及阵型。

2.3.1 仅电机工作

行星齿轮耦合器仅电机工作时，行星齿轮结构的一阶固有频率值为1 790.1 Hz如图3所示，此时电机的转速范围为0～918 r/min，其基频为0～15.3 Hz，由转速的等效杠杆法得出行星轮的转速范围为0～2 075 r/min，其基频为0～34.6 Hz，而行星齿轮机构的一阶固有频率1 790.1 Hz远高于各部件的基频，而且由仿真结果可知随着阶次的增高，其频率值也相应增大。所设计的行星齿轮机构不可能发生共振现象。

图3 第一阶振型图（仅电机工作）

2.3.2 发动机、电机同时工作

行星齿轮耦合器在发动机、电机同时工作时，行星齿轮结构的一阶固有频率值为1 061 Hz。如图4所示，此时电机的转速范围为0～3 645 r/min，其基频为0～60.75 Hz，发动机转速范围为0～1 650 r/min，其基频为0～27.5 Hz，由转速的等效杠杆法得出行星轮的转速范围为0～7 843 r/min，其基频为0～130.72 Hz，而行星齿轮机构的一阶固有频率1 061 Hz远高于各部件的基频，而且由仿真结果可知随着阶次的增高，其频率值也相应增大。所设计的行星齿轮机构不可能发生共振现象。

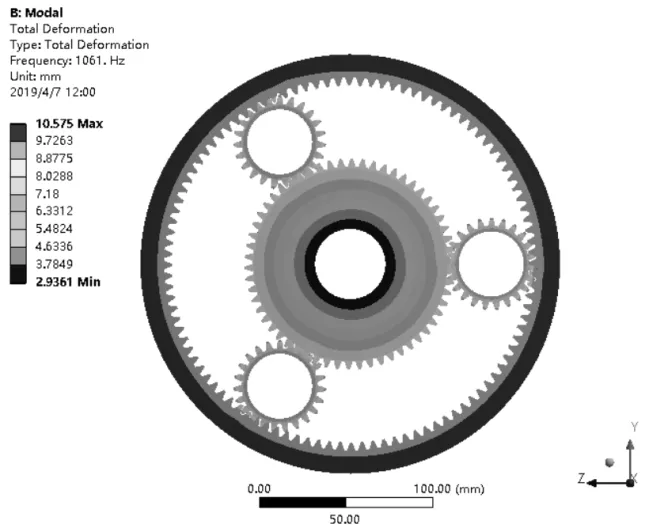
图4 第一阶振型图（发动机、电机同时工作）

2.3.3 电磁锁死控制单元起作用

行星齿轮耦合器在电磁锁死控制单元起作用时，行星齿轮结构的一阶固有频率值为9 601.4 Hz，此时行星齿轮耦合 器的转速范围为1 650～2 150 r/min，其基频为27.5～35.83 Hz，而行星齿轮机构的一阶固有频率9 601.4 Hz远高于各部件的基频，而且由仿真结果可知随着阶次的增高，其频率值也相应增大。所设计的行星齿轮机构不可能发生共振现象。

综上所述，由模态分析结果可知，无论在各个工作情况下，行星齿轮耦合器的固有频率均大于其基频，不会产生共振现象，因此行星齿轮耦合器的设计满足模态要求。

3 总结

利用Solidworks建立了耦合装置的三维实体模型，运用ANSYSWorkbench的静力分析模块，文章对行星齿轮耦合器最大载荷情况进行了强度、刚度分析，同时对各个工作状态进行了模态分析，由分析结果可以看出，行星齿轮耦合器满足各方面设计要求。