课程思政融入高数教学的探索实践

唐凤玲

[摘           要]  根据教学三维目标，解释了课程思政融入高等数学的理论逻辑;结合教学实践，从五个方面讲述了高数教学中蕴含的思政元素;在教学实践中选取高等数学中的两个知识点作为教学实践案例，并对教学实践进行了效果分析。

[关    键   词]  课程思政;立德树人;高等数学;教学内容

[中图分类号]  G642                 [文献标志码]  A              [文章编号]  2096-0603（2021）33-0006-02

课程思政，指以构建全员、全程、全课程育人格局的形式将各类课程与思想政治理论课同向同行，形成协同效应，把“立德树人”作为教育的根本任务的一种综合教育理念。[1]

习近平总书记在2016年12月全國高校思想政治工作座谈会上指出：“做好高校思想政治工作，要用好课堂教学这个主渠道”，“使各类课程与思想政治理论课同向同行，形成协同效应。”[2] 2020年9月9日，习近平总书记在第36届教师节重要寄语中指出，“希望广大教师不忘立德树人初心，牢记为党育人、为国育才使命”。

目前，将课程思政融入专业课课堂教学已成为常态，而如何使之自然融入，实现教学目标与德育目标融合，还需要不断地探索和实践。

一、课程思政融入高等数学的理论逻辑

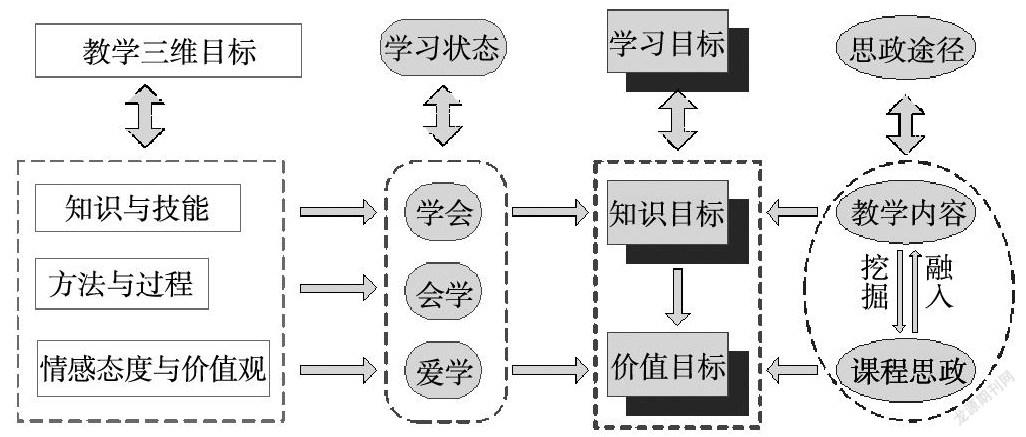
根据布卢姆的教育目标分类理论，结合我国的教育教学现状，即可制订出教学三维目标：知识与技能、过程与方法、情感态度与价值观。其中，第一维是知识目标，第三维则是价值目标。知识目标和价值目标间，并不是割裂的，而是相互联系的关系。如下图所示。

在教学时，三维目标贯穿于课堂始终。知识目标达成主要来自对教学内容的理解和掌握，而价值目标的达成则需要课程思政。教学内容和课程思政之间并不是割裂的，而是相互联系的。在教学设计时，要把课堂所讲内容和课程思政做一体化的设计。教师要善于挖掘教学内容中所蕴含的思政元素，再将思政元素润物细无声般融入教学内容中。

高等数学的课程思政，是指“对高等数学的思想政治教育因素充分挖掘整合，发挥高等数学课程的育人功能，在提高学生数学思维能力的同时，提升思想政治素质，从而内化为一种素质或能力，成为个体认识世界与改造世界的基本能力方法。”[3]这需要对高等数学教材认真钻研，体会每个知识点，从概念、性质、定理和公式等方面，挖掘出蕴含的思政元素。

通过多年教学实践，本人尝试从高等数学中提取思政元素，并将其分为家国情怀、个人品质、辩证思维、价值观和美学修养五个方面。

（一）家国情怀

我国历史上有许多杰出的数学家取得了巨大的成就。在教学中讲述我国数学家的成就，不仅能加强学生的民族自豪感和责任感，还能够激励学生为中华民族的伟大复兴而努力学习奋斗。[4]比如：数列的极限与刘徽的割圆术。

（二）个人品质

高等数学中出现的定理、公式，是数学家们经过勤奋钻研的结果。在教学中，通过讲述数学家的故事，能够吸引学生的注意力，使学生感受数学家优秀的个人品质。比如：欧拉的故事。

（三）辩证思维

数学与哲学想通，其中蕴含着许多辩证思维。在教学中，挖掘高等数学所蕴含的辩证思想，锻炼学生的辩证思维。比如：定积分与唯物辩证法中的量变与质变、否定之否定的辩证思维。

（四）价值观

通过高等数学教学，不仅要教授数学知识，还需要适时传递价值观。比如：连续性和间断点与人生的对应。

（五）美学修养

罗素曾说：“数学，如果公正地看，包含的不仅是真理，还有无上的美——一种冷峭而严峻的美，恰像一尊雕塑一样”。在教学中充分挖掘数学中的美，不仅能激发学生的学习热情，还能提高其美学修养。比如：对“最美”数学公式eiπ+1=0的介绍。

二、课程思政融入高等数学的教学实践

结合前述分析，在备课时，需要考虑教学内容与之相应的价值目标，并用合适的方式切入使目标达成。

教学实践中的两个具体案例：

（一）教学实践案例一“导数的概念”

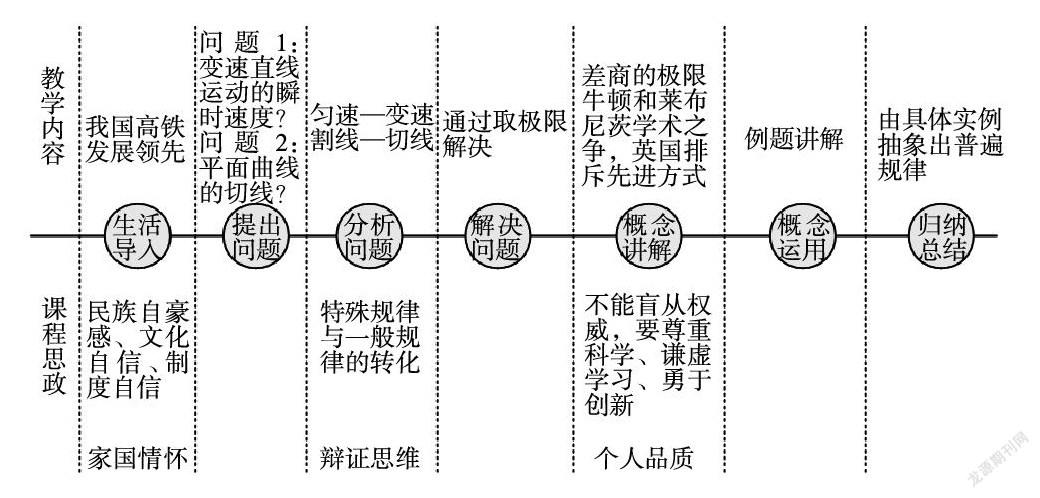
本节课设计的重点，是将课程思政自然地融入导数产生的背景及抽象的概念中去。

课堂上引导学生，从乘坐高铁时观察到的两个细节入手，采用问题驱动模式，运用极限方法开展探究。

首先，考虑到都是交通运输管理专业的学生，所以从高铁行驶短视频导入课堂。通过讲述我国高铁发展的成就，成功激发了学生的爱国情怀和民族自豪感。

其次，结合视频内容，自然提出问题：如何求解变速速率和切线斜率。引导学生通过观察思考匀速与变速之间的异同点、割线斜率与切线斜率之间的异同点，找到彼此之间的内在关系，最终用极限架起之间的桥梁。并启发学生使用辩证思维看问题，前者是特殊现象而后者是普遍现象，它们是具有特殊规律与普遍规律的辩证关系。

最后，在概念讲解中还穿插介绍了数学史：牛顿和莱布尼茨各自独立创立了微积分，但由于对微积分第一发明人地位的争议，英国人拒绝采用莱布尼茨创造的更为便捷的数学符号，导致英国数学脱离了数学发展的时代潮流达一百多年。通过这一段数学史的讲解，进一步使学生明白了不能盲从权威，要尊重科学、谦虚学习、勇于创新。

（二）教学实践案例二“第二重要极限”