动态有向网络中的时序链路预测问题研究
王瑾


摘 要:由于动态向网络具有独特的特征,在对其时序链路预测过程中存在许多问题,为此提出动态有向网络中的时序链路预测问题研究。首先针对动态有向网络特征,采用拓扑结构解决其网络定义问题;利用指数加权滑动平均法对网络时序进行分析,得到T+1时刻预测值,解决时序分析问题;利用聚类算法计算出欧式距离最短的链路路径,解决动态有效网络聚类倾向问题,以此完成动态有向网络中的时序链路预测问题研究。针对上述3个问题提出相对应的解决方法之后,该文中通过仿真实验在真实的动态有向网络中进行了验证,证明通过上述方法解决了相关问题后链路预测效果更佳。
关键词:动态有向网络;时序链路;拓扑结构;聚类算法
中图分类号:TP301 文献标识码:A 文章编号:1001-5922(2021)09-0106-04
Research on the Problem of Time-series Link Prediction in Dynamic Directed Network
Wang Jin
(Shaanxi Institute of Technology, Xi an 710300, China)
Abstract:Due to the unique characteristics of dynamic directed networks, there are many problems in the process of predicting its time-series links. To this end, research on the problem of time-series links in dynamic directed networks is proposed. Firstly, according to the characteristics of the dynamic directed network, the topology is used to solve the network definition problem; the exponentially weighted moving average method is used to analyze the network time series to obtain the time prediction value to solve the time series analysis problem; the clustering algorithm is used to calculate the shortest Euclidean distance chain Road path, to solve the problem of clustering tendency of dynamic and effective networks, in order to complete the research on the problem of time-series link prediction in dynamic directed networks. After the corresponding solutions to the above three problems are proposed, the paper verifies the real dynamic directed network through simulation experiments, and proves that the link prediction effect is better after the above methods are solved.
Key words:dynamic directed network; sequential link; topology; clustering algorithm
0 引言
对于动态有向网络的时序链路预测方法有很多种,比如基于加权算法的时序链路预测方法、基于节点度的时序链路预测方法、基于有向路径的时序链路预测方法等,这些方法有一个共同点是利用动态有向网络的拓扑信息,通过计算动态有向网络结构的相似性,进而预测出网络可能的链路[1]。传统方法虽然在实践中取得了一定的成绩,但是仍然具有一些不足之处[2-5]。传统方法虽然有着良好的实用性,在大多数网络中都能发挥作用,但是缺少针对动态有向网络类型的优化,在对动态有向网络中进行预测时,存在许多问题,因此提出动态有向网络中的时序链路预测问题研究,以提高动态有向网络时序链路预测精度[6-7]。
1 动态有向网络中的时序链路预测问题介绍
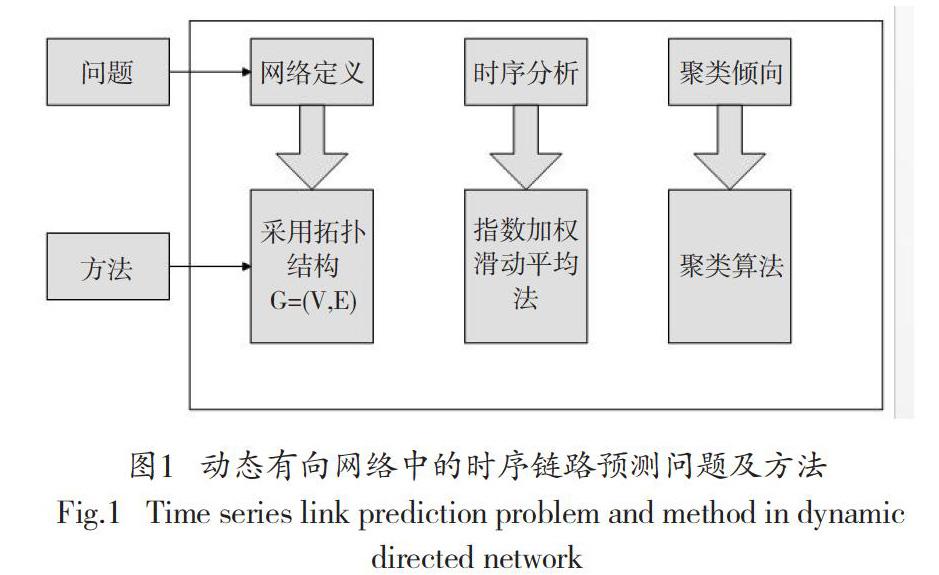
在动态有向网络中,节点之间存在固有的聚类倾向问题,导致预测过程中,很难将这种聚类倾向加以利用;在对时序链路预测过程中,由于動态有向网络不同于静态网络,需要对网络进行准确定义,关系到时序链路预测结果的精准度;面对时序会发展变化的网络,其时序分析也存在一定难度。针对以上提出的动态有向网络时序链路预测问题,提出应对方法,尽可能减小预测误差,提高预测精度。图1为动态有向网络中的时序链路预测问题及方法。
通过采用拓扑结构对动态有向网络进行定义;利用指数加权滑动平均法解决时序分析问题;利用聚类算法对动态有向网络中节点的聚类倾向进行充分利用。下文将针对以上3方面时序链路预测问题进行细致说明。
2 动态有向网络中的时序链路预测问题及对应的 解决方法
2.1 网络定义问题及其解决方法
2.1.1 网络定义问题
此次研究的是动态有向网络的时序链路预测问题,现对于静态网络的链路预测,动态有向网络预测问题更多,首先面临的问题就是网络定义问题。动态有向网络定义与静态网络定义不同,网络是会随着时间的变化而发生变化的动态网络,即在动态网络中顶点的信息与网络中心点的连接结构是随时会发生改变的,显然目前的网络定义不适用于动态网络。
2.1.2 解决方法
动态网络由顶点集合V和顶点之间的关系E组成。将动态网络映射到图论中,其拓扑结构用公式表示如下所示:
公式(1)中,V表示飞控顶点集合;E表示非空边集合。动态网络概要图分为2种,一种是有向图,图中的边都是有方向的,且两边顶点处为起点和终点;另一种是无向图,图中的边是没有方向的。由于此次提出的方法是针对有向动态网络的,所以此次对无向网络不做过多的说明,下文中使用到术语“图”均指的是有向图。有向网络定义图如图2所示。
网络结构中存在5个顶点,如果∈E,那么顶点i和顶点 j是相邻的。顶点i的所有相邻顶点集合记为L(i)。图中顶点i的相邻顶点有顶点g和顶点 j,则它的相邻顶点集合L(i)={g,j}。顶点的degree,指的是网络顶点关联的边的数量,在图中,顶点i是有向网络中的一个顶点,和顶点i关联的边的数量就是顶点i的degree,记为d(i)。图中顶点i的degree为2,记为d(i)=2。对于动态有向网络,图中每个顶点的degree由out degree和in degree组成。顶点i做始点的次数,称为顶点i的out degree,顶点i做终点的次数,称为顶点i的in degree,用数学公式表示如下:
公式(2)中,表示顶点i做始点的次数;din(i)表示顶点做終点的次数。图中顶点i到顶点 j的路径是一个时序顶点序列,路径的长度等于路径上的边的数量,第一个顶点与最后一个顶点相同的路径称之为回路。
由上述可知,此次将动态有向网络定义为一个时间上的有序图集,其拓扑结构为G=(E,V ),E和V分别为网络某时刻的顶点集和变集,E和V会随着时间的变化而变化,符合动态网络随时间变化的特征。
2.2 时序分析问题及其解决方法
2.2.1 时序分析问题
时序分析问题是此次研究的关键问题,链路预测是网络分析中的一个任务,其可以通过观察到的网络中的链路来预测出网络下一时刻链路,目前在该领域的预测方法只是根据网络特定时刻的状态来预测网络新的链路,其并不适用于动态有效网络,导致网络的时序分析成为链路预测过程中的重要问题。常用的时序分析方法有滑动平均法(Moving Average)、平均分析法(Average)、随机时序分析法(Random Walk)、线性回归分析法(Linear Regression)、指数加权滑动平均法(exponentially weighted moving average)等。
2.2.2 解决方法
由于动态有向网络中的链路预测主要是结合网络前T个时刻的信息,预测出网络第T+1时刻的边,针对上文定义的动态有向网络,需要利用时序分析方法对网络所蕴含的时序信息进行分析,针对动态有向网络的链路预测具有一定的随机性,考虑到时间间隔对网络链路预测的影响,此次选择指数加权滑动平均法对网络进行时序分析。对于一个时间序列 ,T+1时刻的预测值可以按照以下公式计算:
公式(3)中,表示动态有向网络T+1时刻预测值;xT表示时刻的观测值;α为平滑系数。对于公式(3)的求解,只需要将迭代的从网络初始时刻计算,就可以得到动态有向网络T+1时刻的预测值。由于动态有向网络初始时刻并没有对应的预测值,所以要实现上述方法对网络时序分析,还需要对网络初始时刻预测值进行取值[2]。如果动态有向网络存在较少的时间序列,则可以取T0时刻的观测值作为T0时刻的预测值,如果动态有向网络存在较多的时间序列,则可以取序列xT0,xT1,xT2的平均值作为初始时刻的预测值,以此解决对动态有向网络时序分析问题。
2.3 聚类倾向问题及其解决方法
2.3.1 聚类倾向问题
由于动态有向网络中数据节点存在聚类倾向特征,导致在时序链路预测过程中,动态有向网络存在聚类倾向。
2.3.2 解决方法
利用聚类算法得到动态有向网络中每个节点的特征,降低预测的维度,对每个网络节点进行聚类分析,解决动态有向网络聚类倾向问题,计算出T+1时刻动态有向网络最短的边,即最短路径,实现时序链路预测[3]。计算每个网络节点到所属类中心的欧式距离,其计算公式如下:
公式(4)中,表示每个网络节点到所属类中心的欧式距离;表示网络节点在顶点集合中的坐标;表示节点所属类编号的类中心坐标。在不同的类中,网络节点数量是不同的,为了方便了解在不同类中的网络节点距离其各自中心的程度,需要对每个网络节点的欧式距离指标进行规范化,使节点所属类具有相同的权重。为了保留原始网络节点的比例特征,此次采用最大规范化方法来统一网络节点,其公式表示如下:
公式(5)中,表示规范化后的网络节点间欧式距离;表示类指标的均值;表示类指标的标准差。该规范化将每个类中的网络节点规范到[0,1]区间内。基于动态有向网络中的物理现象,此处给出聚类系数计算公式:
D的取值如图3所示。
由于sdist值被规范化到[0,1]区间内,节点x和节点y之和取值为[0,2]区间内,从而聚类系数取值为正弦函数的[0,π]区间内。当两节点之和接近零,此时聚类系数值较低,表明此时动态有向网络不存在聚类倾向,动态有向网络之间两顶点之间的距离最短,此条路径为最短有效路径,将该条路径作为结果输出,精准的预测出动态有效网络时序链路。
3 实验验证
在上述环节中对动态有向网络中的网络定义问题、时序分析问题、聚类倾向问题提出相应的解决方法之后,本部分内容通过仿真实验在Facebook-wall中进行了验证,结果如图4所示。
由图4结果可知,在相同的时间窗口下,该文中在解决上述3个问题之后在动态有向网络中链路预测效果有显著的提升,证明了该文中提出的3种方法的有效性。
4 结语
此次针对动态有向网络时序链路预测过程中出现的网络定义问题、时序分析问题、聚类倾向问题进行了研究,并对其提出了相应的解决方法,将研究重点落脚在动态有向网络预测有关问题,有效提高了预测精度。此次研究仍存在优化改进的地方,比如提出的聚类系数存在较强的针对性,不具有较强的普适性,今后还需在该方面进行深入研究,为时序链路预测研究提供理论依据。
参考文献
[1]岳增慧,许海云,王倩飞.基于局部信息相似性的学科引证知识扩散动态链路预测研究[J].情报理论与实践,2020,43(02):84-91+99.
[2]吴晨程,周银座.基于图嵌入法的时序网络链路预测研究[J].杭州师范大学学报(自然科学版),2020,19(05):472-480.
[3]符汉杰,熊赟,朱扬勇.TLP:一个动态网络中的时序链路预测算法[J].计算机工程,2020,46(01):67-73.
[4]杜凡,刘群.有向动态网络中基于模体演化的链路预测方法[J].计算机应用研究,2019,36(05):1441-1445+1453.
[5]杨瑞琪,张月霞.一种时序有向社会网络中的链路预测算法[J].计算机工程,2019,45(03):197-201.
[6]潘嘉琪,邹俊韬.一种基于深度RTRBM的动态网络链路预测方法[J].计算机技术与发展,2020,30(03):1-6.
[7]冯译萱,张月霞.一种时序有向网络中的链路预测方法[J].计算机工程与应用,2019,55(21):151-157.
[8]刘书新,刘群,杜凡.基于模体演化与社区一致性的时序链路预测方法[J].计算机应用研究,2019,36(12):3674-3678+3684.
[9]刘留,王煜尧,倪琦瑄,曹杰,卜湛.一种基于博弈论的时序网络链路预测方法[J].计算机研究与发展,2019,56(09):1953-1964.

