计及风-光出力时变相关特性的输电可靠性裕度评估

高建伟，郭贵雨，郎宇彤，高芳杰，马泽洋

(华北电力大学经济与管理学院，北京市102206)

0 引 言

风电、光伏因具有绿色环保、清洁可持续等优点，现已成为我国电力的重要供应来源。但由于风、光出力存在较强的波动性、不确定性[1-3]，系统需在输电断面中预留合适的输电可靠性裕度(transmission reliability margin，TRM)来确保不确定因素干扰时系统仍能可靠传输[4]，因此，准确评估TRM对保障系统输电可靠性具有重要意义。综上，充分考虑风-光出力相关性生成风-光出力场景，兼顾系统经济性与可靠性构建TRM评估模型，具有较大研究价值。

在风-光出力相关性分析方面，因Copula 函数能较好地刻画多变量间的相关关系，许多学者将其应用在多风电场间或风电场与光伏电站间的相关性分析中。文献[5-6]基于Copula函数分别构建了多风电场间的相关风速模型、相关出力模型，并利用检验方法确定最优Copula函数。但上述文献在运用Copula理论进行分析、建模时，均未考虑场景的动态时序。文献[7-8]基于二维Frank Copula函数建立了每时段风-光联合出力分布函数，进而生成了风-光动态出力场景。上述文献虽然考虑了场景动态时序，但在刻画相关性时仍采用静态Copula函数，未能衡量出力间存在的时变相关特性；同时，在场景生成中，未能很好地刻画风-光出力存在的季节特性。

在TRM评估方面，国内外相关学者进行了较多研究。文献[9]采用固定百分比法，将TRM值按照总输电能力(total transfer capacity，TTC)固定百分比(4%或5%)取值；文献[10-11]采用重复计算法，即在各种运行情况下反复计算得到多个TTC值，其中最大值与最小值之间的差值即为TRM值；文献[12]提出了一种基于模糊随机机会约束规划的TRM计算模型。上述文献未能考虑可再生能源并网对于系统运行的不确定影响，求解的TRM值不能保证系统的可靠运行。文献[13]提出了一种基于保险理论的TRM最优决策模型；文献[14]提出了一种基于随机响应面法的TRM快速求解方法。但上述文献均未考虑TRM的时间尺度特性，不能充分衡量系统运行中的充裕性时序变化；同时，上述文献未能考虑设置TRM后系统可能存在的风险损失，不能充分保障系统的可靠经济运行。

针对上述不足，本文提出一种计及风-光出力时变相关特性的TRM评估方法。首先，考虑风-光出力的时变相关特性与季节特性，提出基于时变Copula函数的风-光24 h联合出力场景生成方法，为后续求解提供基础。其次，考虑TRM时间尺度特性的同时，通过GlueVaR和风险当量系数度量决策者不同风险偏好下的传输能力缺额风险损失，进而构建TRM期望净收益模型。最后，以某地数据为基础，利用序贯蒙特卡洛法模拟生成系统运行场景集，采用改进粒子群优化算法求解模型，验证本文方法在场景生成和保障系统可靠经济运行方面的有效性。

1 风光相关性及时变Copula函数

1.1 风光出力的时变相关特性

分析风-光出力相关性的意义在于掌握风光出力的变化规律，以便更精准地预测其出力大小。在同一区域，相邻风电场与光伏电站间的出力通常存在一定的非线性相关性，某地区一风电场与一相邻光伏电站在典型日24 h内的出力实测数据如图1所示。

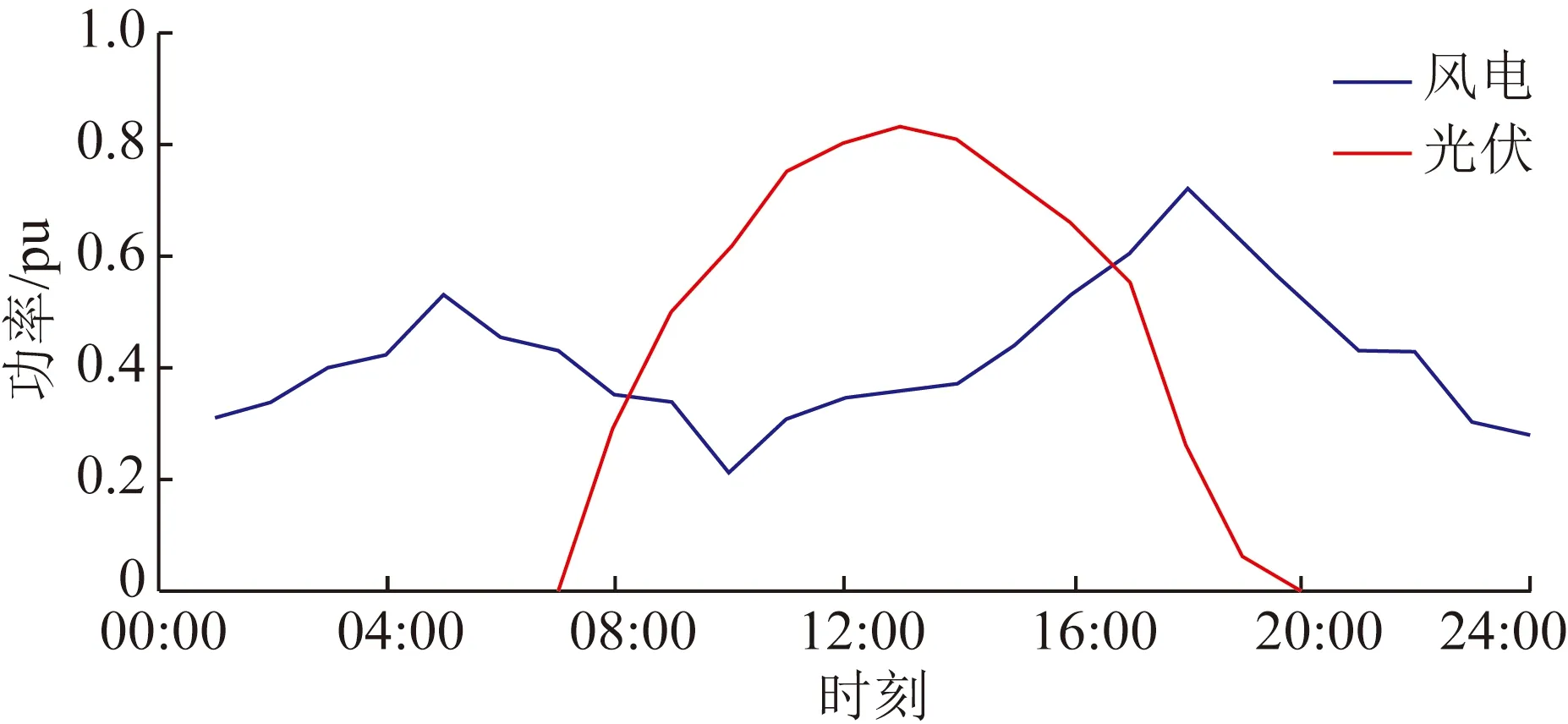
图1 典型日出力Fig.1 Typical daily power output

由图 1 可知，风电与光伏出力在时序上存在一定的相关性，07：00—10：00内风-光出力之间的相关性为负相关，10：00—13：00内风-光出力之间的相关性为正相关，即07:00—13:00内风-光出力必然存在着相关性转变，进而验证了风-光出力间的相关性会随着时间变化而变化，存在着时变特性。

1.2 Copula理论及常用Copula函数

Copula 函数是定义在N维空间内的一个多元分布函数，其实际意义是连接各变量的概率密度函数或边缘分布函数，因此也称为连接函数，理论基础是Sklar定理[15]：令F(·)为具有边缘分布F1(·)，F2(·)，…，FN(·)的联合分布函数，那么存在一个Copula函数C(·)，满足：

F(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN))

(1)

常用的Copula 函数可划分为阿基米德函数族和椭圆函数族2类，前者包括Gumbel-Copula、Clayton-Copula、Frank-Copula，后者包括t-Copula、Normal-Copula，不同Copula函数所能刻画的尾部特征不同。上述Copula均属于静态Copula函数。

1.3 时变Copula函数

静态Copula函数的参数无法跟随时间变化而变化，故仅运用于刻画静态相关性，而时变Copula函数的参数具有时变特征，可运用于刻画时变相关性。因此，本文引入并分析3种常见的时变Copula函数[16]：时变Normal Copula(N-Copula)函数、时变Rotated Gumbel Copula(RG-Copula)函数、时变 Symmetrized Joe-Clayton Copula (SJC -Copula)函数。

1.3.1时变N-Copula函数

时变N-Copula 函数由Normal-Copula 函数衍生而来，该函数不能刻画变量间的非对称尾部相依关系，即对尾部相关不敏感，表达式为：

(2)

式中：u、v为边缘分布函数；ρN,t为时变相关系数;φ-1(·)表示标准正态分布的反函数；s、r为相关变量。

1.3.2时变 RG-Copula函数

时变 RG-Copula 函数由Gumbel-Copula 函数衍生而来，该函数对下尾相关敏感；对上尾相关不敏感，即上尾相关系数为0，表达式为：

CRG(u,v|ρRG,t)=exp{-{[-ln(1-u)]ρRG,t+
[-ln(1-u)]ρRG,t}1/ρRG,t}

(3)

式中：ρRG,t为时变相关系数。

1.3.3时变 SJC-Copula函数

时变SJC-Copula 函数由Joe-Clayton Copula函数衍生而来，该函数对于上、下尾相关均敏感，故时变SJC-Copula 函数在相关性分析中的使用更为广泛，表达式为：

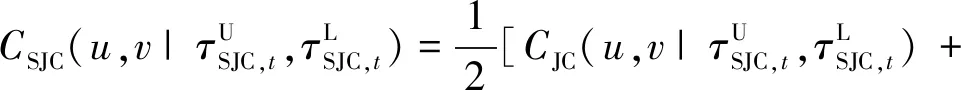
(4)

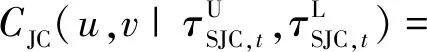
(5)

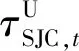
1.4 拟合优度检验方法

为确定最优Copula函数，本文利用赤池信息量准则(Akaike information criterion，AIC)[17]和贝叶斯信息量准则(Bayesian information criterion，BIC)[18]作为拟合优度检验方法，表达式为：

AIC=2k-2lnL

(6)

BIC=klnn-2lnL

(7)

式中：k为模型参数个数；L为极大似然估计值；n为样本数量。模型拟合优劣可由准则值直接体现，其大小与拟合优度成反比。

2 基于时变Copula生成系统运行场景集

计及时变相关特性，引入时变Copula函数生成风-光联合出力场景集，据此生成系统运行场景集。首先，获取历史风光出力的标幺化数据，利用AIC、BIC确定最优Copula函数。其次，利用非参数核密度估计方法生成每时段风、光出力的边缘概率密度函数，通过最优Copula函数构建风-光联合出力分布函数。然后，生成每时段累积概率值，并利用3次样条插值法求解对应时段的风-光出力值。最后，以风-光出力场景为基础，结合节点负荷及元件运行状态生成系统时序运行场景。

2.1 确定最优 Copula函数

以某地区一光伏电场和一相邻风电场2011年全年的标幺化出力数据(每小时采样1次)为基础，利用AIC、BIC对比不同Copula函数的拟合优劣，结果如表1所示。

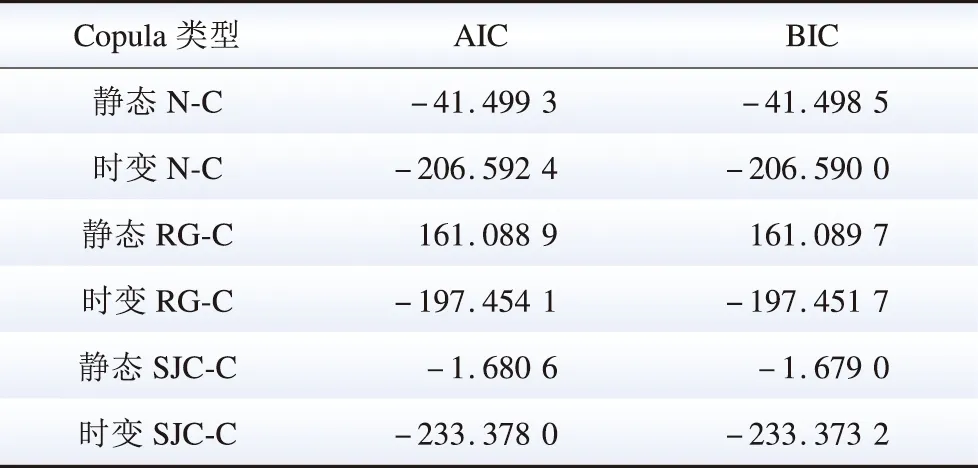
表1 拟合优度对比Table 1 Comparison of goodness of fit

从表1可知：当采用相同结构的Copula函数时，时变Copula的拟合优度明显高于静态Copula；最优Copula函数为时变SJC-Copula函数。

2.2 风-光出力场景的生成与削减

1)划分风、光出力数据。

由于风、光出力具有明显的季节特性，本文根据季节的时间尺度(春季90天、夏季91天、秋季92天、冬季92天)将全年(365天)数据划分为过渡季(春、秋两季)、夏季、冬季。

2)生成风、光边缘分布函数。

面对总量大且难以准确得到边缘分布的风、光出力数据，采用非参数核密度估计方法处理此类数据的效果最佳[19]。根据上述三段季节性出力数据，利用非参数核密度估计法生成各季节每时段风、光出力概率密度函数，表达式为：

(8)

(9)

式中：sr为某季节，具体计算时分为过渡季(ts)、夏季(su)、冬季(wi)；xt,sr、yt,sr为某季节下t时段的风、光出力，t=1,2,…,24；dsr为某季节的总天数；Xit,sr、Yit,sr为某季节下第i天的t时段风、光出力；h为窗宽；K(·)选取高斯核函数，以风电为例：

(10)

对式(8)、(9)求得的季节性风、光出力概率密度函数进行积分变换，得到对应的边缘分布函数FXt,sr(xt,sr)、FYt,sr(yt,sr)。

3)构建风-光联合出力分布函数。

考虑风-光联合出力存在时变相关特性，本文以历史数据为基础，通过时变相关系数序列和时变Copula函数构建风-光联合出力分布函数。

首先，将上述全年数据等效看作365个风-光出力场景，根据划分的三段季节，通过K-means聚类进行聚类(K=3)，得到各季节的典型出力场景并获取各场景的风、光出力时序数据。

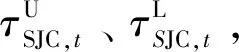
(11)

(12)

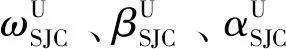
分别为上、下尾演进方程中的待估参数；Λ′(x)=(1+e-x)-1为logistic变换函数，保证其取值在(-1,1)内；m为数据窗口，默认取10；d为随机选择典型场景的某一个，d=1,2,3；xt,d、yt,d分别为第d个典型场景的t时段风、光出力值。

最后，确定选取的典型场景所代表的季节后，求得该季节各时段的风、光出力边缘分布函数，进而结合时变相关系数序列与时变 SJC-Copula函数构建第s个场景的风-光24 h联合出力分布函数，表达式为：

(13)

式中：s=1,2,…,S，S为场景总数；ut=FXt,sr(xt,sr)，vt=FYt,sr(yt,sr)。

构建联合出力分布函数的流程如图2所示。

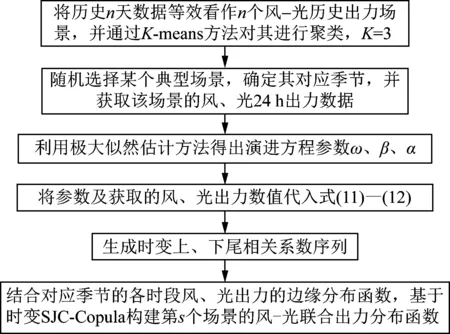
图2 联合出力分布函数的构建Fig.2 Construction of joint output distribution function

4)生成风-光出力场景。

由于利用非参数核密度估计方法得到的概率密度函数难以求解其边缘分布函数及对应的反函数，所以本文利用3次样条插值法计算第s个场景的风、光出力值[8]。

首先，利用式(8)、(9)求得第s个场景对应季节的每时段风、光概率密度曲线，并将风、光出力区间分别等分为n-1个子区间，同时，对应的累积概率区间也被等分为n-1个子区间。

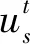
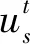
(14)

(15)

式中：i=1,2,…,n-1；ai、bi、ci、li为多项式系数。

5)生成风-光出力场景集。

上述流程3)—4)反复进行直至生成S组初始风-光出力场景。为保证后续TRM计算的速度与精度，利用同步回代消除法削减初始场景数至指定阈值H[21]，同时，生成风-光出力场景集。

2.3 生成系统24 h运行场景集

在风-光出力场景集的基础上，结合元件运行状态、节点负荷状态生成系统24 h运行场景集。

2.3.1元件运行状态模型

本文只考虑常规发电机与输电线路这2种元件的运行状态且考虑状态校正，其每时段运行状态η作为随机变量服从二次型分布，表达式分别为：

(16)

(17)

式中：η=1，表示元件正常运行；η=0，表示元件停运；KG,i为常规发电机组i停运的概率，i=1,2,…,Nk，Nk为常规发电机组总个数；KL,ij为输电线路ij停运的概率，i=1,2,…Nn，j=1,2,…Nn，Nn为节点总数。

2.3.2节点负荷模型

本文中各时段的系统节点负荷，均相互独立且服从正态分布N(μ，σ2)，表达式为：

(18)

式中：μ为期望值；σ为标准差。

基于时变Copula函数生成系统时序运行场景集的整体流程如图3所示。

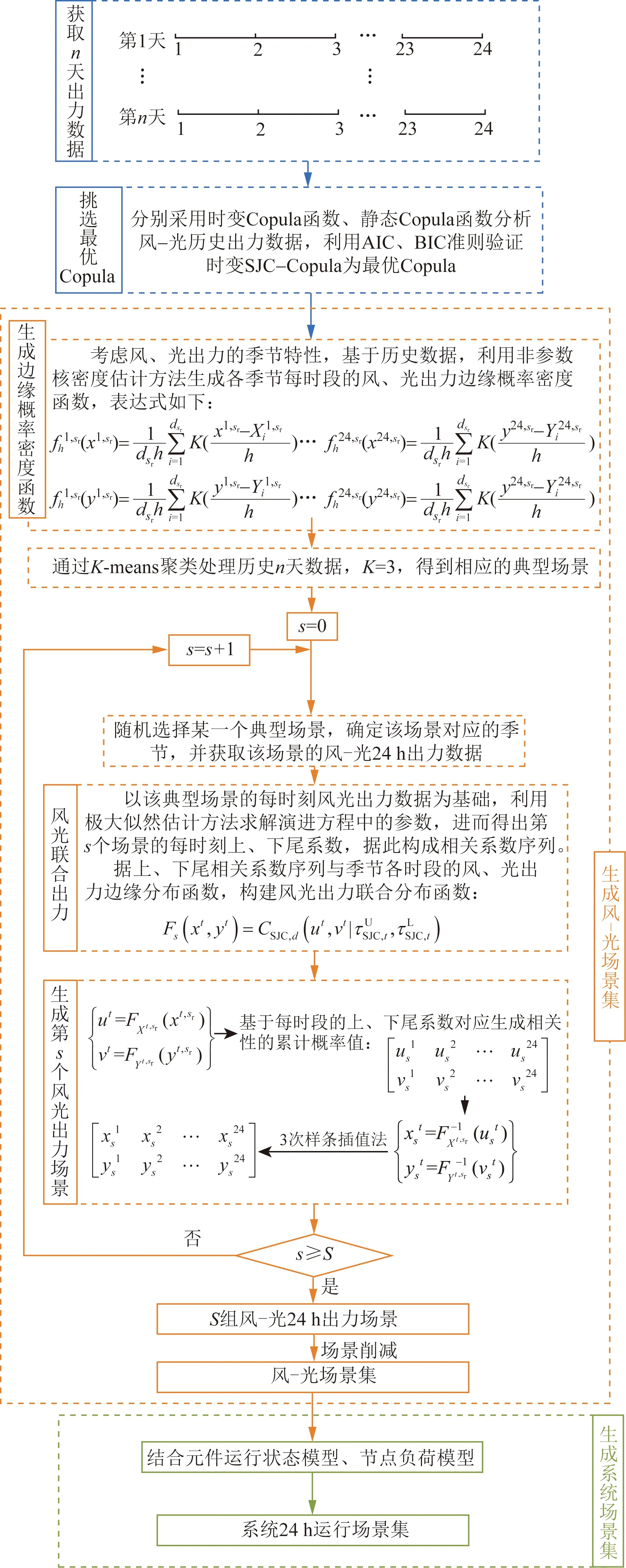
图3 系统运行场景集生成流程图Fig.3 Flowchart of system operation scenario set generation

3 TRM期望净收益模型

3.1 传输能力跌落

系统24 h运行场景中存在多种不确定因素，如风-光每时段出力、常规机组与输电线路故障停运等，这些因素会对输电断面的总传输能力产生干扰，导致断面实际传输能力低于预计传输能力，称出现“传输能力跌落”，设置TRM的实际意义即为抵御部分或全部的传输能力跌落。传输能力跌落的产生与抵御如图4所示。

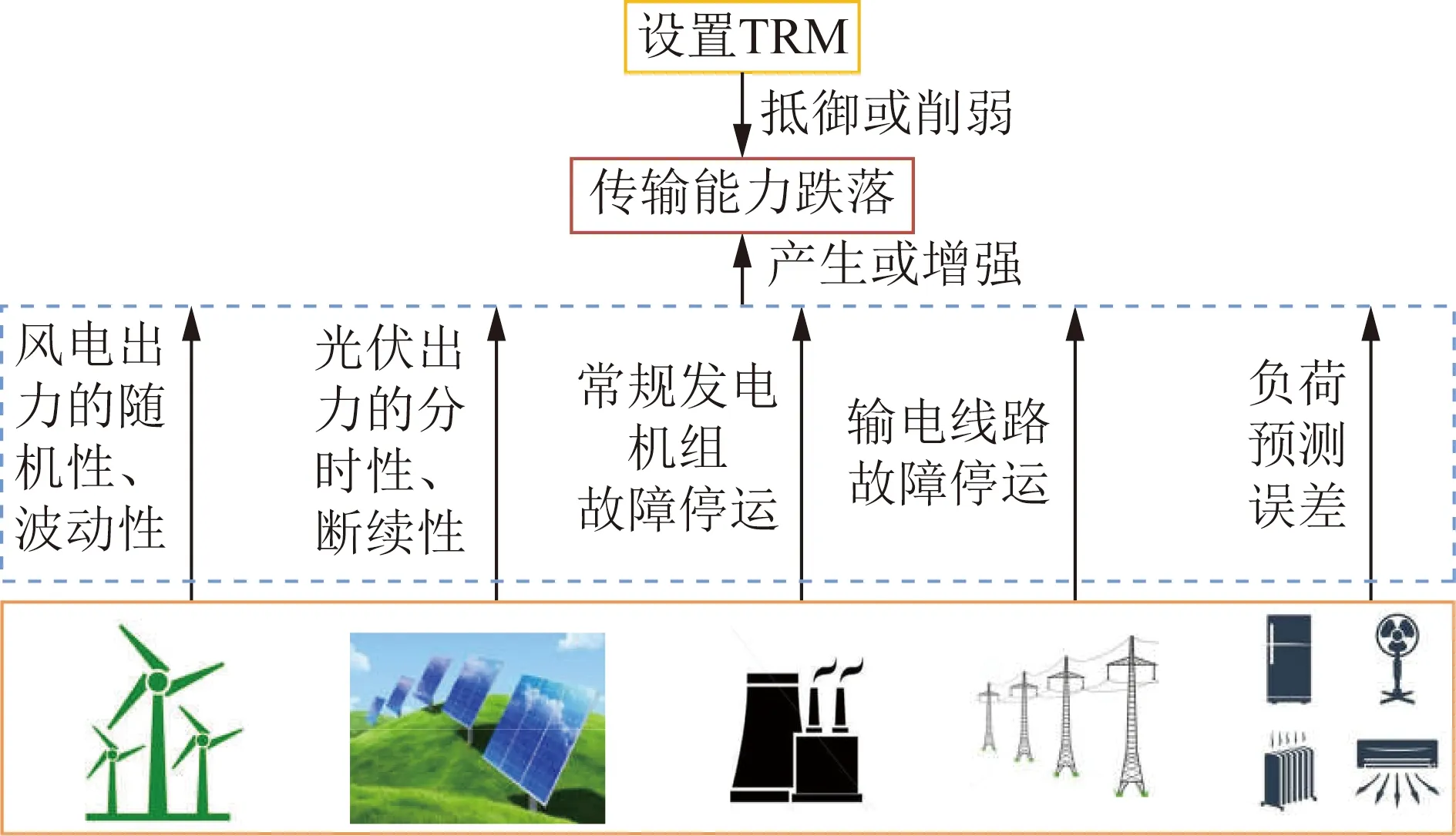
图4 传输能力跌落的产生与抵御Fig.4 Generation and resistance of transmission capacity drops

3.2 目标函数

模型以设置TRM给互联电力系统带来的期望净收益最高为目标，假定“传输能力跌落”出现的概率为pl，目标函数表达式为：

maxB(u)=pl[Bu-Ca(u)]-(1-pl)Ca(u)-Vloss(u)

(19)

各部分计算如下：

1)TRM成本。

一定时间跨度Δt内，TRM成本为预留TRM容量为u时对传输参与方的全部机会成本，记为Ca(u)，表达式为：

Ca(u)=Cg(u)+Cd(u)

(20)

Cg(u)=pguΔt-FuΔt

(21)

Cd(u)=(pd-pg)uΔt

(22)

式中：Cg(u)为发电方的全部收益损失；Cd(u)为售电方的全部收益损失；pg为上网电价；F为每MW·h发电变动成本；pd为终端销售电价。

2)TRM收益。

TRM收益Bu指设置TRM为u时抵御部分传输能力跌落所给系统带来的损失支出减少量[13]，表达式为：

(23)

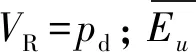
(24)

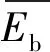
(25)

(26)

式中：H为削减后保留的场景个数；PTTC,f为区域间最大TTC；PTTC,si为场景si下实际运行TTC；K′是TRM为u裕度仍不足的场景个数；PTTC,k为裕度不足时第k个场景的实际运行TTC；PTTC,f、PTTC,si、PTTC,k均采用重复潮流法计算。

3)传输能力缺额损失。

在系统输电断面中设置TRM，若因设置TRM值过低而不足以抵御全部传输能力跌落从而导致互联电力系统产生的潜在损失，本文定义该损失为传输能力缺额损失Vloss(u)，表达式为：

Vloss(u)=ηr·QGlueVaR,u

(27)

各部分表示如下：

(1)风险当量系数。

定义风险当量系数ηr为：衡量在规定置信水平下1 MW的传输能力缺额对于系统造成的潜在经济损失。表达式为：

ηr=(pd-pg)·γ

(28)

式中：γ为风险偏好因子。当决策者为风险厌恶时，γ>1；当决策者为风险中立时，γ=1；当决策者为风险喜好时，γ<1。

(2)传输能力缺额风险。

因TRM设置不足而不能抵御全部传输能力跌落，这时输电断面实际传输能力与最大传输能力间的差额，称为传输能力缺额，表示为：

(29)

Qu={Qu,i},i=1,…，H

(30)

式中：Qu,i为第i个场景的传输能力缺额均值；Qu为各场景下传输能力缺额均值的集合。

定义Qu,i的不确定性即为传输能力缺额风险，本文引入GlueVaR[22]对其风险进行刻画。相比于其他风险度量工具，GlueVaR在满足一致风险度量条件的同时，还有效地刻画了决策者的不同风险偏好与风险度量的关系，表达式为：

(31)

式中：α、β为置信水平，0≤α≤β≤1；h1、h2为生存概率，0≤h1≤h2≤1；w1、w2、w3为权重，其值反映决策者的不同风险偏好，w1=h1-[(h2-h1)(1-β)/(β-α)]、w2=(h2-h1)(1-α)/(β-α)、w3=1-w1-w2。

(32)

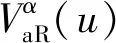
(33)

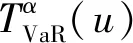
(34)

式中：QGlueVaR,u表示TRM设置为u时系统传输能力的期望缺额，即传输能力跌落风险的严重程度。

3.3 约束条件

1)等式约束。

潮流约束：

(35)

(36)

式中：Vi、Vj为节点i、j的电压幅值；θij为相角差；Pi、Qi为节点i的有功负荷值、无功负荷值；j∈i表示与节点i相连的所有节点；Bij、Gij分别为节点导纳矩阵的虚部元素、实部元素。

2)不等式约束。

节点电压约束：

Vimin≤Vi≤Vimax

(37)

线路容量约束：

Sij,min≤Sij≤Sij,max

(38)

节点出力约束：

0≤Pi≤Pr

(39)

式中：Vimin、Vimax为节点i的电压幅值最小、最大值；Pi为节点出力大小；Pr为节点额定出力；Sij、Sij,min、Sij,max分别为线路ij的传输容量及其最小、最大值。

3.4 模型求解算法

相比于非线性优化方法，元启发式算法通过一群独立的个体并行地探索搜索空间且通常不要求目标函数的可微性、连续性等特定性质，因此能够在避免局部最优的同时，提高计算速度。

在元启发式算法中，粒子群优化(particle swarm optimization，PSO)算法适合求解多约束非线性规划问题，而改进粒子群优化(improved particle swarm optimization，IPSO)算法较PSO算法改进了惯性权重因子，引入了速度系数，弥补了PSO算法容易陷入局部最优的缺陷[23]。另外，考虑序贯蒙特卡洛模拟方法可以弥补非序贯蒙特卡洛模拟方法不能衡量TRM时间尺度特性的缺陷。因此，本文采用基于序贯蒙特卡洛模拟方法的IPSO算法求解模型。

4 算例分析

4.1 算例描述

本文采用修改后的IEEE-RTS系统，基于230 kV(售电)区域至138 kV(购电)区域间的输电断面研究TRM问题[14]。为简化模型计算，购电区域的负荷增长按照各自的功率因数等比例增加，功率因数保持不变。节点19处接入风电场，节点20处接入光伏电站。模型参数：pg为65美元/(MW·h)；F为40美元/(MW·h)；pd与VR均为75美元/(MW·h)；系统参数参考文献[24]，输电线路故障率设为0.005。算法参数[23]：惯性权重因子w的取值区间为[0.4，0.9]；调整系数c为-0.9；速度因数δ为0.5；加速因子c1和c2均为2；种群规模大小为50；迭代次数为500次。修改后的系统如图5所示。

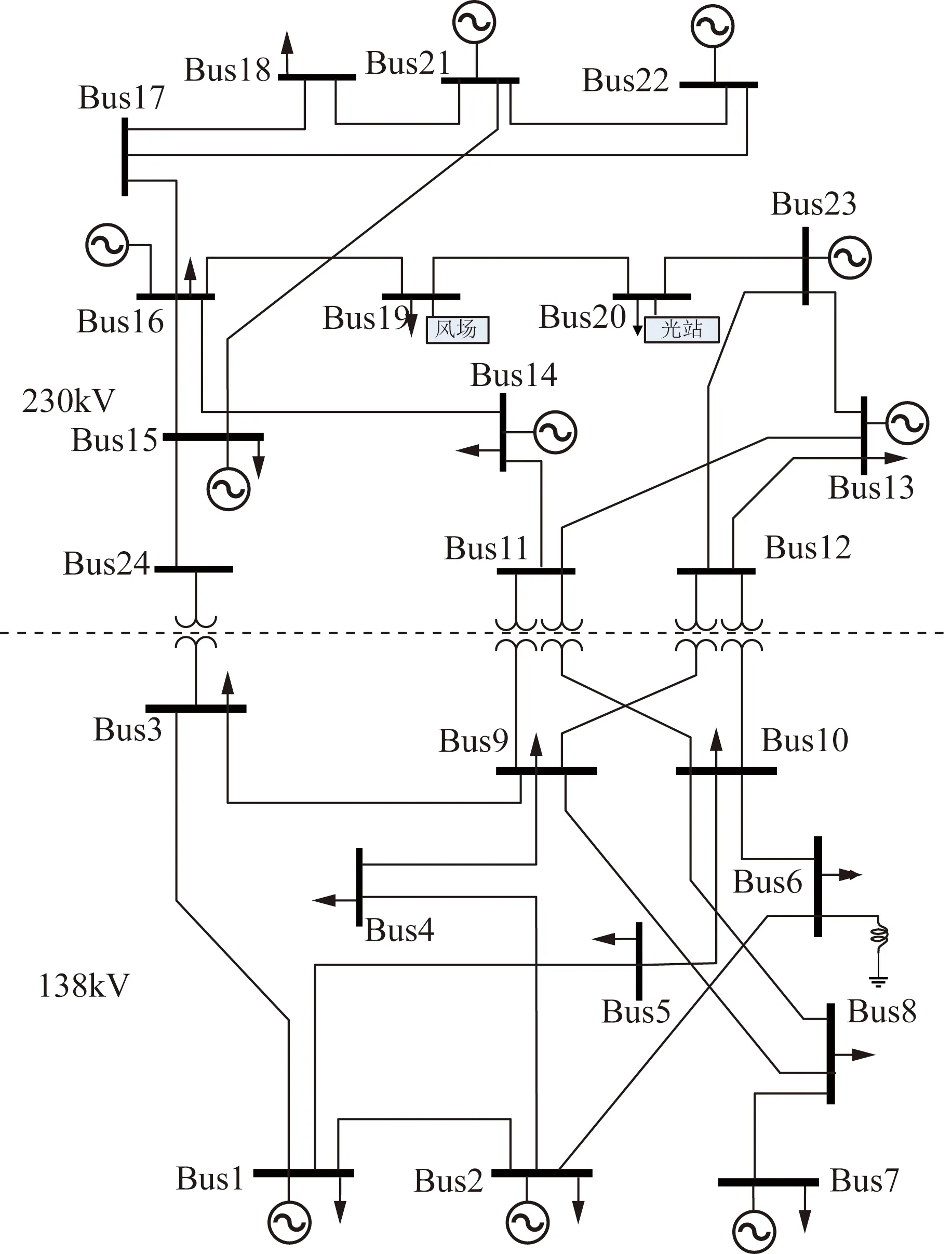
图5 IEEE-RTS系统图Fig.5 IEEE-RTS system diagram

4.2 算例求解流程

算例求解流程如图6所示。

4.3 风-光出力场景生成方法验证

4.3.1场景生成结果

首先，根据季节特性进行划分，将一年划分为春、夏、秋、冬4个季节(春、秋两季归为过渡季)。

其次，利用K-means聚类方法对4.2节的风-光场景集进行聚类处理，K=3。最后，得到3个典型风-光24 h联合出力场景，其具体出力值如图7所示。

从图7可知，每个典型场景均具有一定的时序性与季节性，且在某些时段内风-光的出力变化呈现一致或相反，体现了其时变相关特性和互补性。结合该区域的季节性出力可知：场景1风电场出力较高但光伏出力较低，具有冬季特性；场景3风电场出力较低但光伏出力较高，具有夏季特性；场景2具有过渡季特性。

4.3.2对比不同场景生成方法

静态最优Copula函数的确定对于不同场景生成方法的对比具有重要意义。Frank-Copula函数能较好地刻画风-光的负相关互补关系[7]，因此，基于2.1节中的历史数据，利用AIC、BIC准则对比表1中N-Copula函数与Frank-Copula函数确定静态最优Copula函数，结果如表2所示。

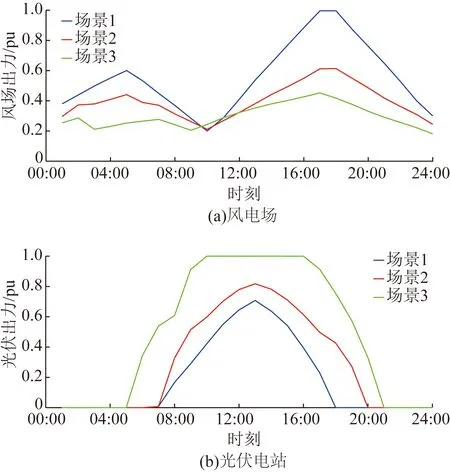
图7 风-光联合出力典型场景Fig.7 Typical scene of wind-solar joint output

表2 确定静态最优Copula函数Table 2 Determination of the static optimal Copula function

由表2可知，静态最优Copula函数确定为静态Frank-Copula函数。对比静态和时变场景生成方法的具体流程如下：

1)将全年风-光出力数据等效为365个24 h出力场景，并采用K-means对其聚类，K=3(仅考虑过渡季、夏季、冬季)。

2)利用文献[8]所提方法，基于静态Frank-Copula函数生成3 000组出力场景，同理，采用K-means对其聚类得到典型场景，K=3。

3)根据本文2.2节所提方法生成3 000组出力场景，聚类步骤、阈值与步骤2)相同。

4)将步骤2)、3)中的典型场景分别与步骤1)中对应的典型场景进行对比，分别计算各时段出力数据之间的差值并相加。本文定义该差值为距离值df-h，距离值与场景生成效果成反比，即距离值越低则场景生成效果越符合实际，其拟合优度越高。

(40)

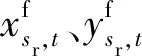
表3 不同场景生成方法距离值Table 3 Distance values of different scene generation methods

从表3可知，基于时变Copula函数所生成的场景，精度更高且更贴合实际，进而验证了本文所提方法对静态Copula方法有较好弥补，能为求解TRM模型提供更有效的场景数据。

4.4 TRM模型分析

4.4.1模型必要性

首先，风电场、光伏电站的装机容量均设置为100 MW；然后，计算每个典型场景的每时段传输容量跌落均值，在分析模型必要性时忽略负荷波动及元件故障发生，结果如图8所示。

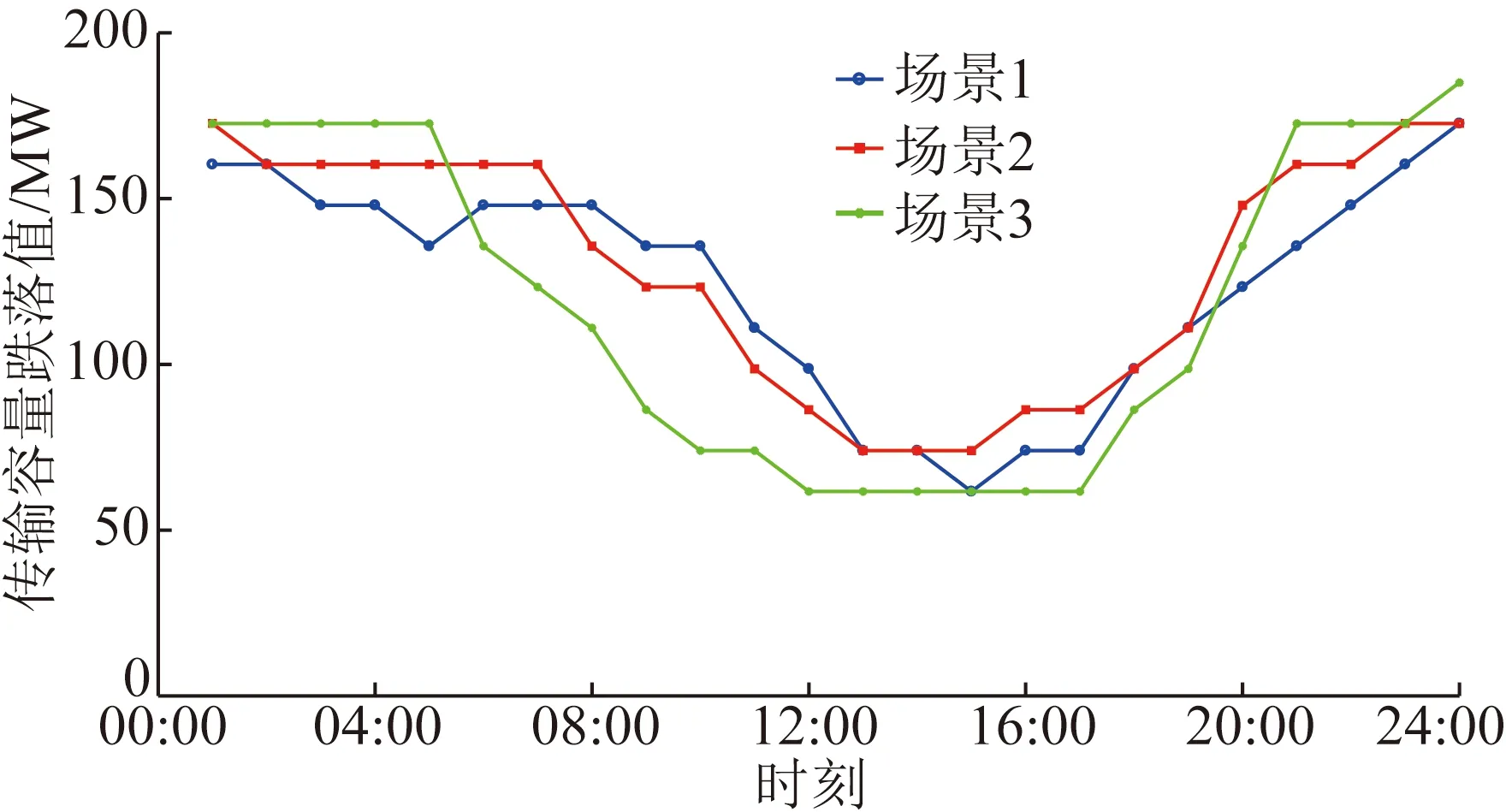
图8 典型场景每时刻传输容量跌落值Fig.8 Transmission capacity drop value at each moment in typical scenarios

从图8可知，互联电力系统由于引入风-光随机性电源，导致系统在运行期的每时段内均存在不同程度的传输能力跌落。因此，在风-光并网背景下，考虑TRM的时间尺度特性来构建经济有效的TRM评估模型具有重要意义。

4.4.2模型有效性

以4.2节中的3 000组系统运行场景为基础，计算每个运行场景的传输能力跌落均值，其中最大值为418.648 MW，故TRM取值区间设为[0,400] MW。置信水平β=99.5%，α=95%，决策者不同风险偏好可由GlueVaR中的不同权重大小来表示：当决策者为风险厌恶时，w1=1,w2=0，w3=0，γ=1.5；当决策者为风险中立时，w1=w2=w3=1/3，γ=1；当决策者为风险喜好时，w1=0,w2=0，w3=1，γ=0.5。决策者呈不同的风险偏好时，TRM与期望净收益的对应关系如图9所示。

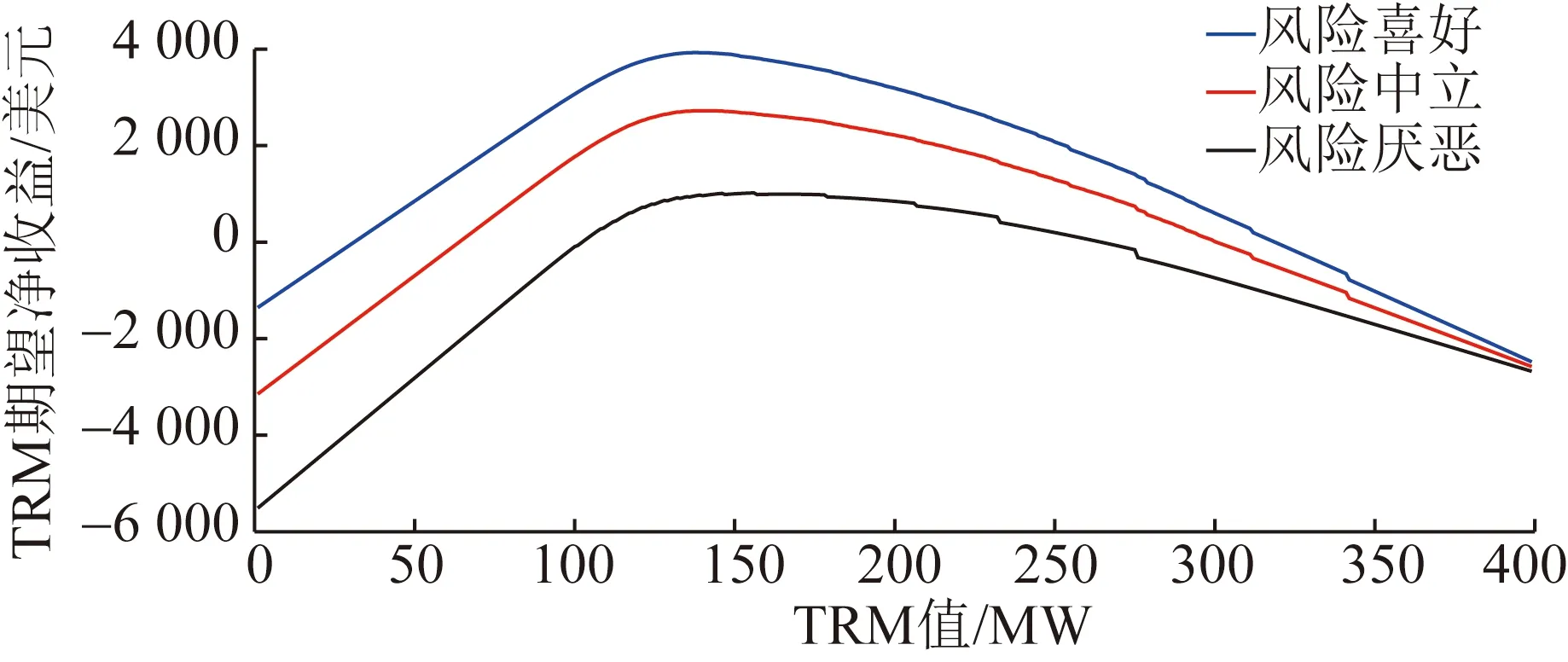
图9 TRM与对应期望净收益Fig.9 TRM and corresponding expected net income

当决策者分别为风险喜好、风险中立和风险厌恶时，通过IPSO算法求解TRM最优值，相应的迭代过程如图10(a)、(b)、(c)所示，最优TRM值和对应的期望净收益值如表4所示。

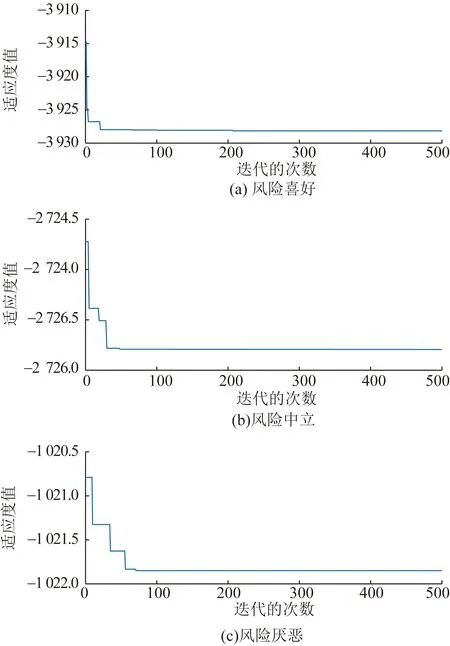
图10 不同风险偏好下的迭代过程Fig.10 Iterative process under different risk preferences

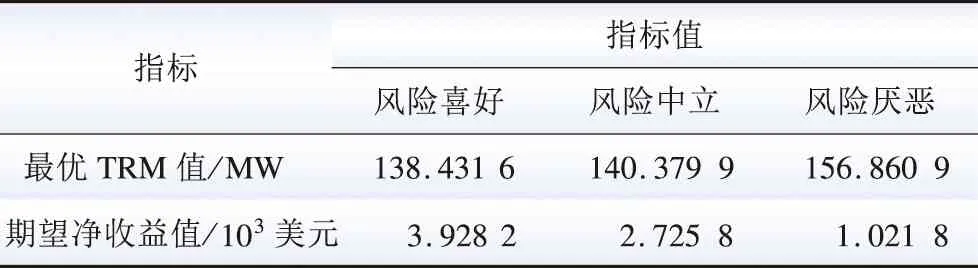
表4 不同风险偏好下的最优TRM值和期望净收益值Table 4 Optimal TRM values and expected net profit values under different risk preferences

由表4结果可知，模型能够考虑不同风险偏好下的跌落风险损失以实现TRM评估差异化，进而验证了该模型能够满足风-光并网下互联电力系统的灵活运行要求。

TRM作为充裕性资源，其意义是为保障电能在区域间的可靠传输，故在实际评估时决策者更偏向风险厌恶。为进一步验证本文模型的实际意义，当决策者为风险厌恶时，TRM分别取表4中不同决策偏好下的最优TRM值，计算对应的期望净收益值，结果如表5所示。

表5 风险厌恶下设置不同TRM的期望净收益值Table 5 Expected net profit values when setting different TRM under risk aversion

由表5可知，求解结果进一步验证了该模型具备有效性与经济性，能够在实际评估时为决策者提供一定参考。

4.4.3对比不同TRM计算方法

引入风-光等不确定性电源后，采用传统方法计算得出最优TRM值与净收益期望值，并与本文方法进行对比，如表6所示。

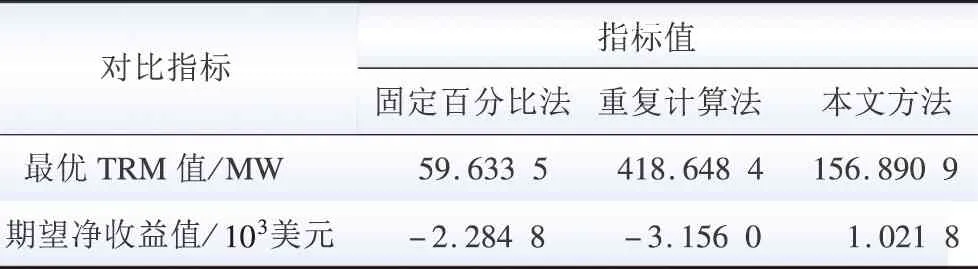
表6 不同TRM计算方法对比Table 6 Comparison of different TRM calculation methods

传统方法求解的TRM值过于保守或偏激，不能保证风-光并网形势下互联电力系统的可靠、经济运行，而本文方法得到的TRM指标值对系统运行做到了收益最大化，对以往方法有较好弥补。

5 结 论

综上，为更好保障互联电力系统的输电可靠性，本文提出了一种计及风-光出力时变相关特性的TRM评估方法。基于考虑时变相关特性和季节特性的风-光场景集，提出了区分决策者不同风险偏好的TRM评估方法，通过求解算例并对比分析，得出以下结论：

1)基于时变Copula函数的风-光场景生成方法能有效提高场景精度，拟合数据更贴近实际，并为准确求解TRM模型提供有效保障。

2)TRM期望净收益模型不仅保障了系统的可靠经济运行，而且区分了不同风险偏好以实现TRM差异化评估，满足了系统灵活运行要求。

3)考虑TRM的时间尺度特性，采用基于序贯蒙特卡洛模拟的IPSO算法求解，得到的TRM值能更好地保障系统的运行充裕性。