基于改进模型预测控制的电-气系统新能源功率波动平滑策略

余洋，贾浩，陈启维，范亚洲，米增强，袁玉宝，常生强

(1.新能源电力系统国家重点实验室(华北电力大学(保定))，河北省保定市 071003)；2.河北省分布式储能与微网重点实验室(华北电力大学(保定))，河北省保定市 071003)；3.石家庄科林电气股份有限公司，石家庄市 050222)

0 引 言

对于某些特定应用场景，集合了分布式电源、储能装置、可控负荷与常规负荷的微电网为新能源发电并网提供了诸多便利。然而，微网内风电、光伏等新能源出力具有随机性和间歇性，功率变化时间尺度小至几秒，大至数小时[1-2]，造成了联络线功率频繁波动[3]。当前主要利用储能装置对不同频率成分的波动功率予以补偿[4]，如文献[5]利用小波分解对新能源出力进行频谱分析，然后根据频率特性运用储能装置平抑新能源功率；文献[6]提出了一种平滑风电功率的混合储能控制策略，通过滤波方法将波动功率分解为不同频率成分，以超级电容补偿高频分量，蓄电池补偿低频分量。储能装置功率易调节，但是存在两方面问题：一是初期投资相对较大，二是采用大容量储能后期维护较为困难[7]。

近年来，需求侧温控负荷(thermostatically controlled load,TCL)作为优质的可调度资源，以投资小、响应速度快、调控灵活等特点，成为了平抑新能源功率波动的重要手段之一，聚合建模是首先需要解决的问题。文献[8]利用状态队列模型控制聚合温控负荷(aggregated TCLs,ATCLs)的开关状态进而控制聚合功率，代替储能装置用于平滑联络线功率波动。文献[9]研究了基于耦合Fokker-Plank方程的ATCLs双线性时间连续聚合模型。不过现有建模方法中模型参数获取较困难，且模型阶次较高。本文将以温控负荷聚合功率为变量建立ATCLs双线性模型，采用欧拉法对模型进行离散化处理，具有模型参数容易获取、计算复杂度低等优势。合理的控制方法是ATCLs参与功率调控的另一个关键点，主要有滑模控制、模糊控制、智能PID控制和模型预测控制(model predictive control，MPC)等。如文献[10]采用反推控制原理，对ATCLs与发电机励磁进行协调控制。相比其他算法，MPC具有配置容易、能在线处理约束、可有效解决非线性动态问题等优点[11-12]，适合用于ATCLs调度控制。文献[13]建立了一种ATCLs的二维状态箱模型，采用MPC对ATCLs功率进行调节，为电网提供辅助服务。然而，受用户舒适度指标约束，采用ATCLs单一手段的可调节范围有一定限制。当前，以燃气轮机为耦合的电-气互联综合能源系统快速发展，为平滑联络线功率波动提供了一个新的可行手段，如文献[14-15]引入了微型燃气轮机(micro-turbine,MT)参与功率调控，但使用的MT模型过于简单，且未考虑内部机理与具体功率控制方法。对于MT，常见的控制算法有：PID控制、反步法和MPC等[16]，文献[17]提出了基于MPC的MT功率调节方法，结果表明机组进入稳态的时间优于PID控制，且稳定性更好。可见，在ATCLs和MT的控制中，MPC均获得了广泛的应用。不过传统MPC虽解决了离散操作变量的潜在优化问题，但计算负担较重、寻优时间较长[18]，有必要对其进行改进以减少计算量、缩短寻优时间。

在对联络线功率进行经验模态分解(empirical mode decomposition,EMD)基础上，本文创新性地设计了ATCLs与MT共同抑制联络线功率波动的调控策略。同时针对传统MPC寻优时间较长的问题，采用Lyapunov稳定性理论改进传统MPC算法，提出基于Lyapunov函数的MPC方法，提高算法运算速度，缩短寻优时间，并保证控制的稳定性。通过改进MPC算法构造虚拟控制量以分别控制ATCLs和MT，有效实现电-气互联系统中新能源功率波动平滑。算例仿真表明，本文控制方法能够使它们的输出功率有效跟踪各自参考值，兼顾温度舒适度与调节范围，较好地满足联络线功率波动平滑要求。

1 电-气互联系统控制结构

本文研究对象是由电网、天然气网组成的电-气互联综合能源系统，如图1所示，MT可看作电-气互联系统的中枢，微网中有ATCLs、不可控负荷和分布式电源，分布式电源包括风电和光伏。图1中蓝色箭头代表电能流向，黄色箭头代表天然气流向，红色色块代表参与调节的可控单元，蓝色色块代表不可控单元，灰色色块代表上级电网，黄色色块代表天然气侧单元，Gf表示天然气网向MT提供的燃料量。

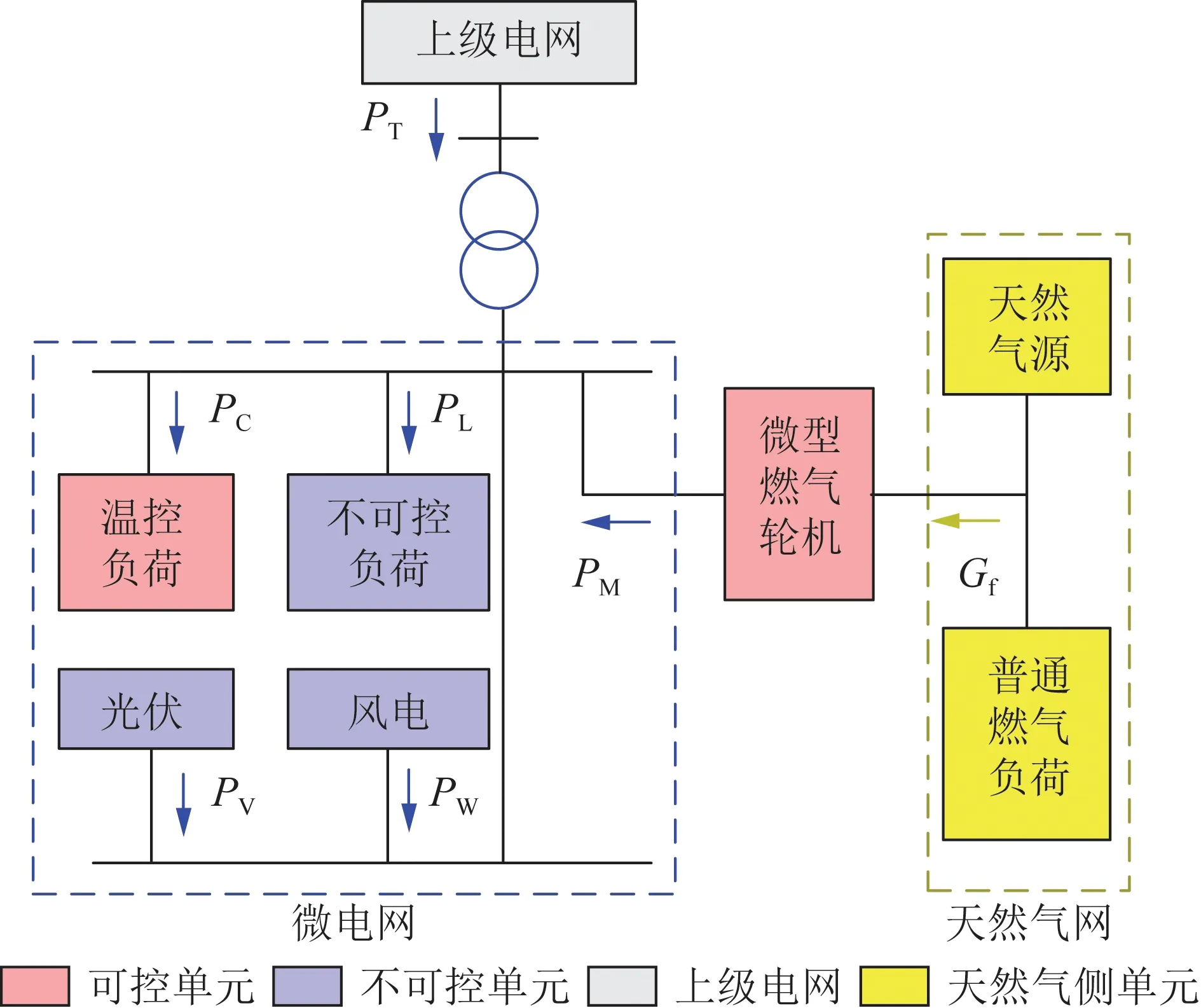
图1 电-气互联系统结构Fig.1 Electricity-gas interconnection system structure

可知微电网的功率平衡关系为：

PT+PV+PW+PM=PC+PL

(1)

式中：PT为联络线功率，取电网向微电网注入功率为正；PV与PW分别表示光伏与风电的发电功率；PM代表MT的输出功率，不参与调节时处于额定运行状态；负荷包括可参与功率调节的ATCLs功率PC和不可参与调节的常规负荷PL；PV与PW的随机变化会造成PT的波动。

图2给出了联络线功率控制流程，本文采用ATCLs与MT协调控制的策略平抑联络线功率波动，以达到用户舒适度与调节范围的平衡。首先，采用式(2)表示的EMD将原始联络线功率分解为一系列包括不同频率成分的固有模态分量(intrinsic mode function,IMF)和残差项r，然后用ATCLs平抑由前m项组成的高频成分，用MT平抑剩余分量和残差组成的低频成分。

(2)

式中：Pi表示分解后的第i个IMF分量，i=1，2，···，n，n为分解后IMF分量的总个数；r为残差项；Ch为高频分量之和，由EMD分解后前m个IMF分量求和而得；m由试差法根据MT的约束而定[13]；Cl为低频分量之和，是原信号除去Ch之后的剩余信号之和。

图2 本研究整体结构Fig.2 Overall structure of the study

波动功率的平衡关系为：

(3)

2 电-气互联系统的建模

2.1 ATCLs模型

面向控制的ATCLs双线性聚合模型具有较高的建模精度[11]，模型建立如下：

(4)

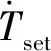
2.2 MT模型

本文选取Rowen单轴燃气轮机为研究对象，将原动机与发电机统一建模[16]：

(5)

式中：δ为发电机功角，以弧度为单位；ω为发电机相对角速度；mf为压气机排放环节输出；wf为燃烧室排放环节输出；ω0为发电机额定角速度；D为发电机阻尼系数；H为发电机惯性常数；A、B、C为燃气轮机扭矩计算模块参数；M、N为发电机功角特性系数；PG为原动机功率；E′q为q轴暂态电势；Vs为电网电压；X′d为d轴暂态电抗；Xq为q轴电抗；Tc为压气机排放延迟时间常数；c1、c2和b为模型等效简化系数；Gf为天然气网输入燃料量。

2.3 其他模型

本研究中电-气互联系统还考虑了风电、光伏等不可控电源和不可控负荷，其中不可控负荷采用恒功率模型表示。

1)风电出力模型。风力发电的随机性是由风速的随机变化造成的，其出力PW可计算如下：

(6)

式中：ρ为空气密度；S为垂直于风速的截面积；vW为风速。

2)光伏出力模型。由光伏阵列的等效电路，可得到光伏出力PV模型：

(7)

式中：I为电池组件输出电流；Iph为给定光照强度下的短路电流；I0为二极管的饱和电流；V为电池组件终端电压；VT为组件热势能；Rs为固有电阻；a为二极管理想常数；Ns为串联组件个数；Np为光伏阵列并联个数。

3)天然气及其管网模型。本研究中天然气网内有天然气源、普通燃气负荷、天然气管道等元件，其中，天然气源用燃气量无限大的恒压源模型表示；普通燃气负荷以恒流量节点模型表示；天然气流在天然气管网中的流动时延长、惯性大，故有必要对天然气管道进行单独建模，相应的模型如下：

(8)

式中：pout为管道的出口压力；pin为管道的入口压力；Mout为管道的出口流量；Min为管道的入口流量；va为天然气中声音的传播速度；Sa管道横截面积；L为发电机惯性常数；d为管道直径；f为摩擦系数。

3 应用于电-气互联系统新能源功率波动平滑的改进MPC方法

3.1 传统MPC工作原理

传统MPC控制流程一般分为预测模型、滚动优化、反馈控制3步，对于功率控制问题，在k时刻，预测模型可描述为：

P(k+1|k)=g[P(k),u(k+1|k)]

(9)

式中：P(k)为k时刻实际测量的功率值；u(k+1|k)为k时刻作用于k+1时刻的控制量；P(k+1|k)为k时刻通过预测模型得到的k+1时刻的功率预测值。同时通过式(10)可得到预测步长内所有采样点的功率预测值。

(10)

式中：P(k+i|k)为k时刻通过预测模型得到的k+i时刻的功率预测值；Np为预测步长。

在k时刻，对成本函数的优化可表示为：

(11)

式中：Pf(k+i)为k+i时刻的功率参考值；Q为权重系数。优化可得k时刻一组控制量{u(k+1|k),u(k+2|k),…,u(k+Np|k)},取u(k+1|k)作为最优控制量作用于k+1时刻。

由于输出功率预测难免存在误差，可将输出功率反馈到MPC，对预测模型进行优化，完成反馈校正。

但传统MPC存在不足之处，一方面，每一次迭代都需优化计算，且对每个采样时间的预测值还需进行成本函数评估，尤其是在较长的预测时间尺度和较高的采样频率下，将其应用于新能源功率波动平抑会面临计算量较大、寻优时间较长的问题；另一方面，传统MPC无法保证控制的稳定性。

3.2 基于Lyapunov函数的改进MPC

为解决上述问题，本文提出了基于Lyapunov稳定性理论的改进MPC方法。基本原理是基于被控对象的状态空间模型，利用Lyapunov函数直接推导出控制律，得到优化控制量，并将得到的优化控制量作用于下一时刻。

1)改进MPC用于ATCLs的高频分量控制。

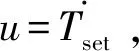
(12)

式中：T′为离散时间步长。

令聚合功率误差函数为：

(13)

则：

(14)

选取Lyapunov函数：

(15)

Lyapunov函数的变化率为：

ΔLt{e(k+1)}=Lt{e(k+1)}-Lt{e(k)}

(16)

根据Lyapunov稳定性定理，为了让输出信号准确跟踪参考信号，Lyapunov函数的变化率应为负，令：

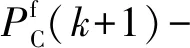
(17)

式中：λ为控制增益，取值范围为[-1,1]。

当λ取值均在[-1,1]范围内时，系统逐渐趋于稳定，可得控制律为：

(18)

2)改进MPC用于MT的低频分量控制。

令x1=δ，x2=ω，x3=mf，x4=wf，u2=Gf，则采用隐式欧拉法得到离散MT模型为：

(19)

式中：T为离散时间步长。

(20)

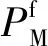
利用Lyapunov函数的变化率构造虚拟控制量，控制律设计如下。

1)设计转速虚拟控制量。

令功角误差函数为：

e1(k)=x1(k)-x1f(k)

(21)

则：

e1(k+1)=T{ω0[x2(k+1)-1]}+
x1(k)-x1f(k+1)

(22)

选取Lyapunov函数：

(23)

Lyapunov函数的变化率为：

(24)

根据Lyapunov定理，为了让输出信号能够准确跟踪参考信号，Lyapunov函数的变化率应为负，可令：

T[ω0(x2(k+1)-1)]+x1(k)-x1f(k+1)=
λ1e1(k)

(25)

式中：λ1为功角控制增益，取值范围为[-1,1]。

构造转速虚拟控制量为：

(26)

2)设计压气机排放环节输出虚拟控制量。

类似于转速虚拟控制量的推导过程，设计的压气机排放环节输出虚拟控制量如式(27)所示。

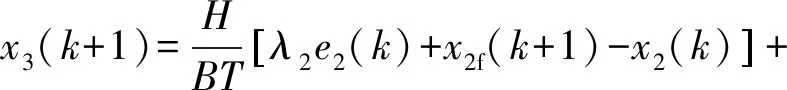
(27)

式中：e2为转速误差函数；λ2为转速控制增益，取值范围为[-1,1]。

3)设计压气机排放环节输出虚拟控制量。

压气机排放环节输出虚拟控制量见式(28)。

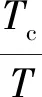
(28)

式中：e3为压气机排放环节输出误差函数；λ3为压气机排放环节输出控制增益，取值范围为[-1,1]。

4)设计实际控制律。

基于以上分析，再经过一些推导过程，设计最终的实际控制律为：

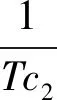
(29)

式中：e4为燃烧室排放环节输出误差函数；λ4为燃烧室排放环节输出控制增益，取值范围为[-1,1]。

3.3 改进MPC的优势

在ATCLs功率控制中，利用Lyapunov函数直接推导出控制律式(18)，得到优化控制量，在MT功率控制中，利用Lyapunov函数直接推导出控制律式(29)，得到优化控制量，并将得到的优化控制量作用于下一时刻，省去了传统MPC式(11)的复杂优化过程。

因此，基于Lyapunov函数的MPC方法避免了传统MPC通过滚动优化对每个采样点的预测值评估成本函数的过程，提升了计算速度，并且更为重要的是，还能保证控制的稳定性。

4 算例仿真及分析

根据图1所示的电-气互联系统进行仿真分析，互联系统内包括：额定功率为1 kW的空调设备共800台，室内温度舒适度范围为[20,24]℃，用户可接受的最大温度波动范围为0.5 ℃[19-20]；额定功率为300 kW的MT两台，功率运行范围为[90,300]kW，则MT总输出功率的上下限分别为600 kW和180 kW，MT模型参数见表1[21]。采样频率取为1 min，24 h的风电、光伏和不可控负荷的功率如图3所示。

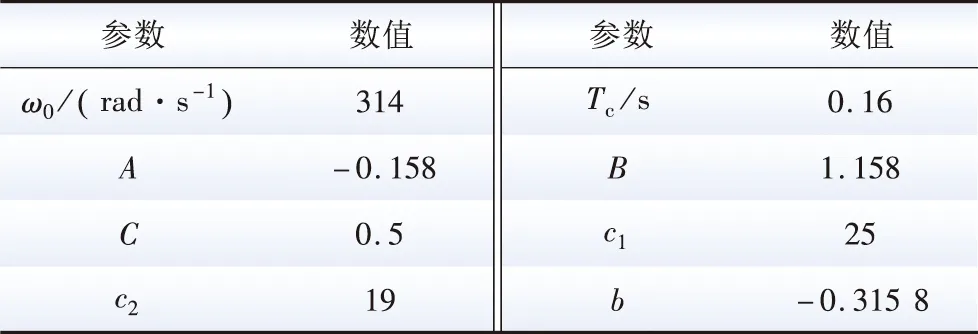
表1 MT模型参数Table 1 Model parameters of the MT

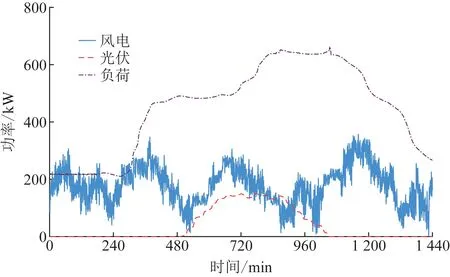
图3 光伏、风电及不可控负荷曲线Fig.3 Curves of PV,wind power and uncontrollable load

1)ATCLs阶跃响应。首先让聚合温控负荷接受阶跃响应指令，图4(a)所示为控制指令增发200 kW，当控制增益λ取[-1,1]范围内不同值时的功率响应曲线，在取值范围内控制增益越小达到稳态的调节时间越短，但误差越大。通过试错法可得同时满足调节时间要求与误差要求的控制增益取值λ=0.5，可在满足功率调节时间的基础上使功率误差最小化。

为了验证改进MPC算法对ATCLs的控制性能，图4(b)、(c)为控制增益取λ=0.5，在控制指令增发200 kW时ATCLs功率与20个温度区间内温控负荷数量的响应情况。可见，在改进MPC的控制下，随着ATCLs不同温度区间内的温控负荷数量的变化，功率逐渐变大直到达到稳态值800 kW。

如图4(b)所示，改进MPC调节时间约为3.1 s，与传统MPC相比，改进MPC算法控制效果更优。在Windows 10操作系统，Intel Core i5-8250U 1.8 GHz 处理器，8 GB RAM内存，MATLAB R2016b平台下进行仿真，改进MPC所用求解计算自用时间为0.084 s，缩短了约23%。

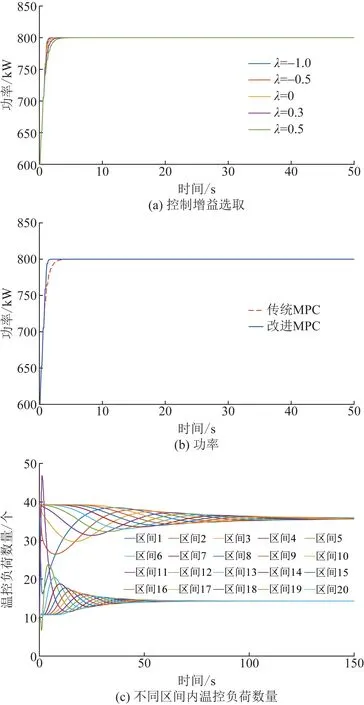
图4 ATCLs状态量曲线Fig.4 Changing curves of state variable for ATCLs

2)MT阶跃响应。让单台MT在稳定运行状态时接受阶跃响应指令，图5(a)所示为在5 s时负荷由80%上升至90%，当控制增益λ2、λ3、λ4取-1时，λ1取[-1,1]范围内不同值时的功角响应曲线，在取值范围内控制增益越小达到稳态的调节时间越短，但误差越大。通过试错法可得同时满足调节时间要求与误差要求的控制增益取值为λ1=0，λ2=-1，λ3=-1，λ4=-1，可在满足功率调节时间的基础上使功角误差最小化。

为了验证改进MPC算法对MT的控制性能，图5(b)、(c)、(d)为控制增益取λ1=0，λ2=-1，λ3=-1，λ4=-1，在5 s时负荷由80%上升至90%的MT响应情况。可见，在改进MPC的控制下，MT各状态量将随之变化，最后到达稳态，此时，天然气网供给燃料量由初始值0.136 4逐渐上升至稳态值0.170 5，压气室与燃料室排放量经过一定延时后随之上升，转速短暂上升后恢复至额定转速，功角变大直到达到稳态值，符合MT的工作机理。

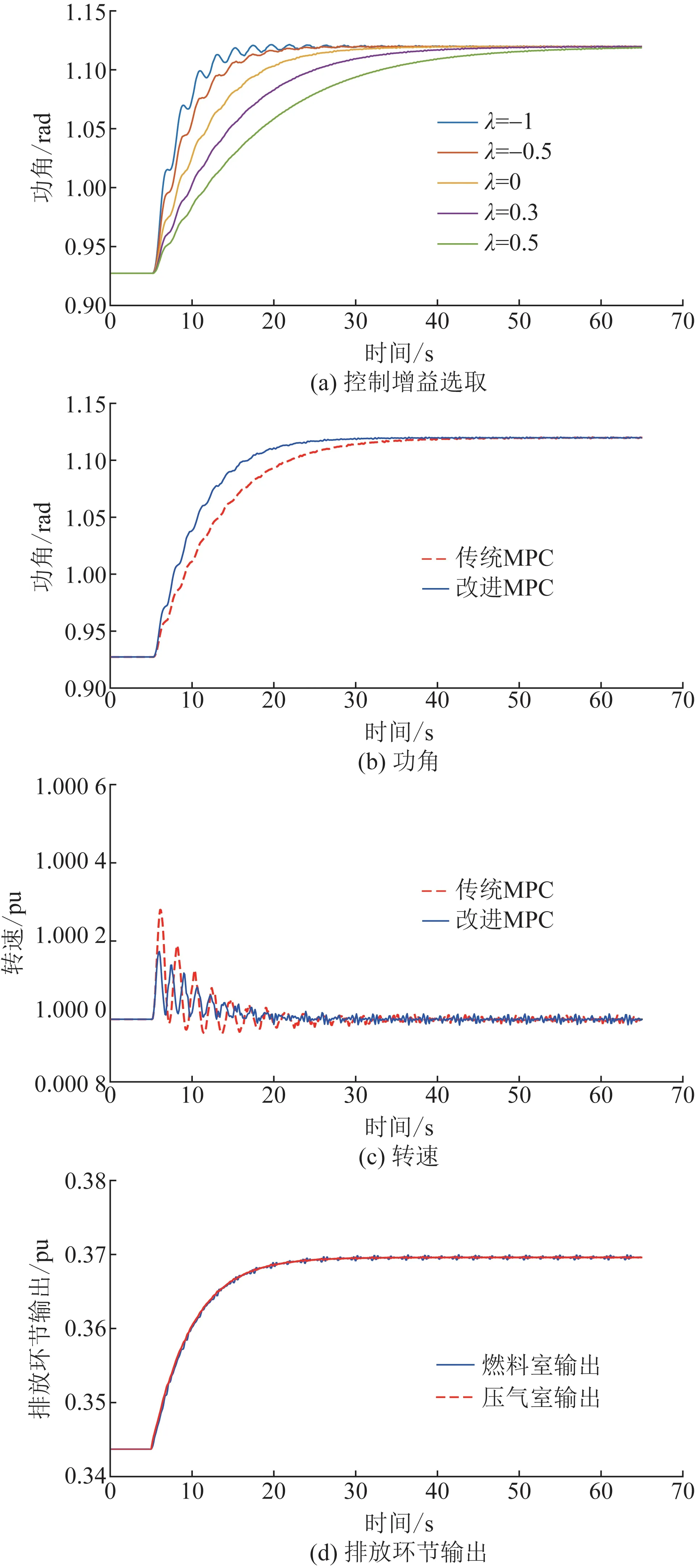
图5 MT状态量曲线Fig.5 Changing curves of state variable for MT

MT常规控制性能指标要求为功率相对控制精度0.3%，转速相对误差2%[22]，本文改进MPC方法控制性能参数完全满足常规控制性能指标，调节时间约为25.5 s，与传统MPC相比，改进MPC算法对于各个控制量的效果更优，计算时间更短，控制精度更高，且在MATLAB平台仿真求解计算自用时间为0.096 s，缩短了约25%。

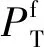
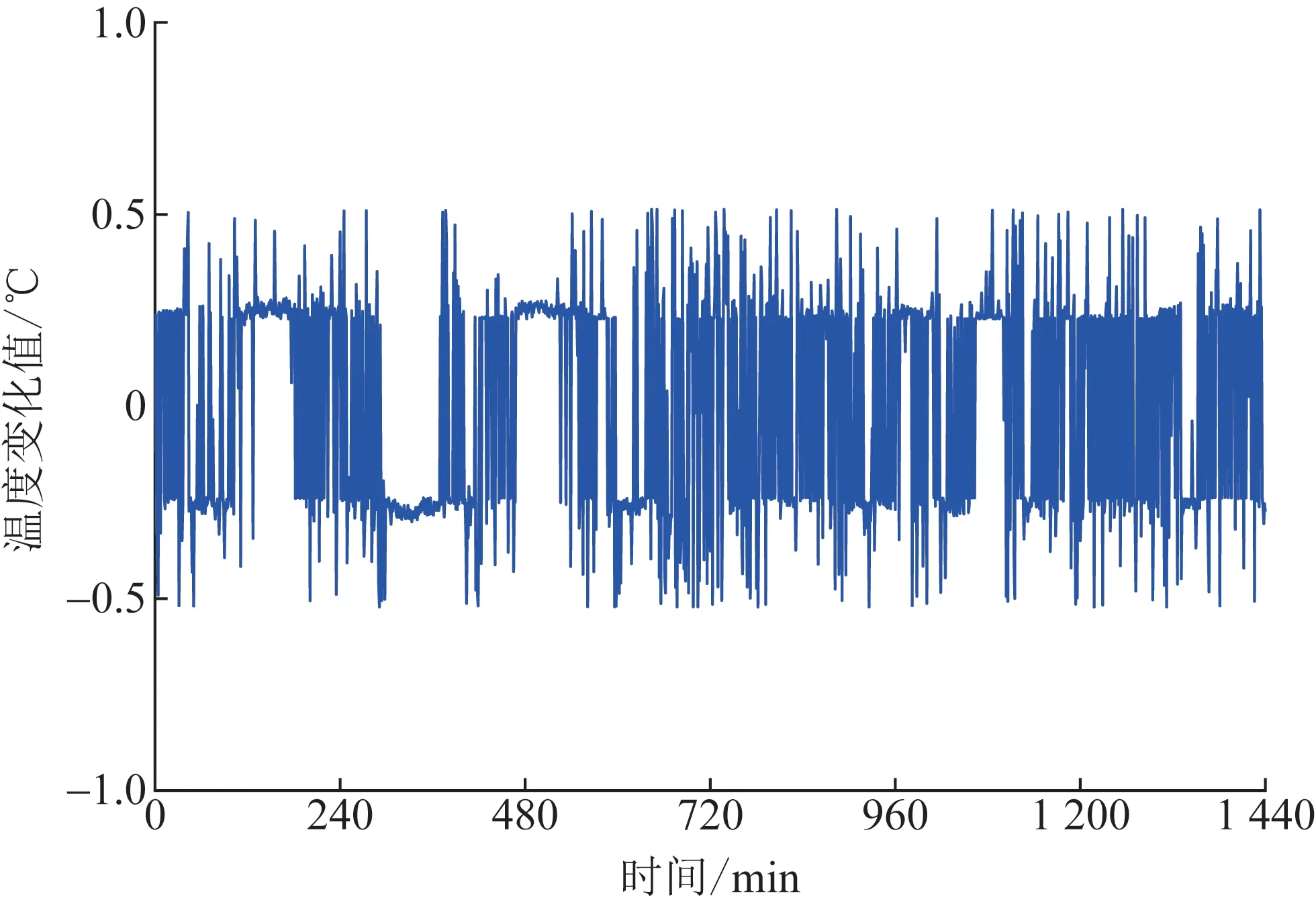
图7 温度设定值变化曲线Fig.7 Changing curve of temperature setting value for ATCLs

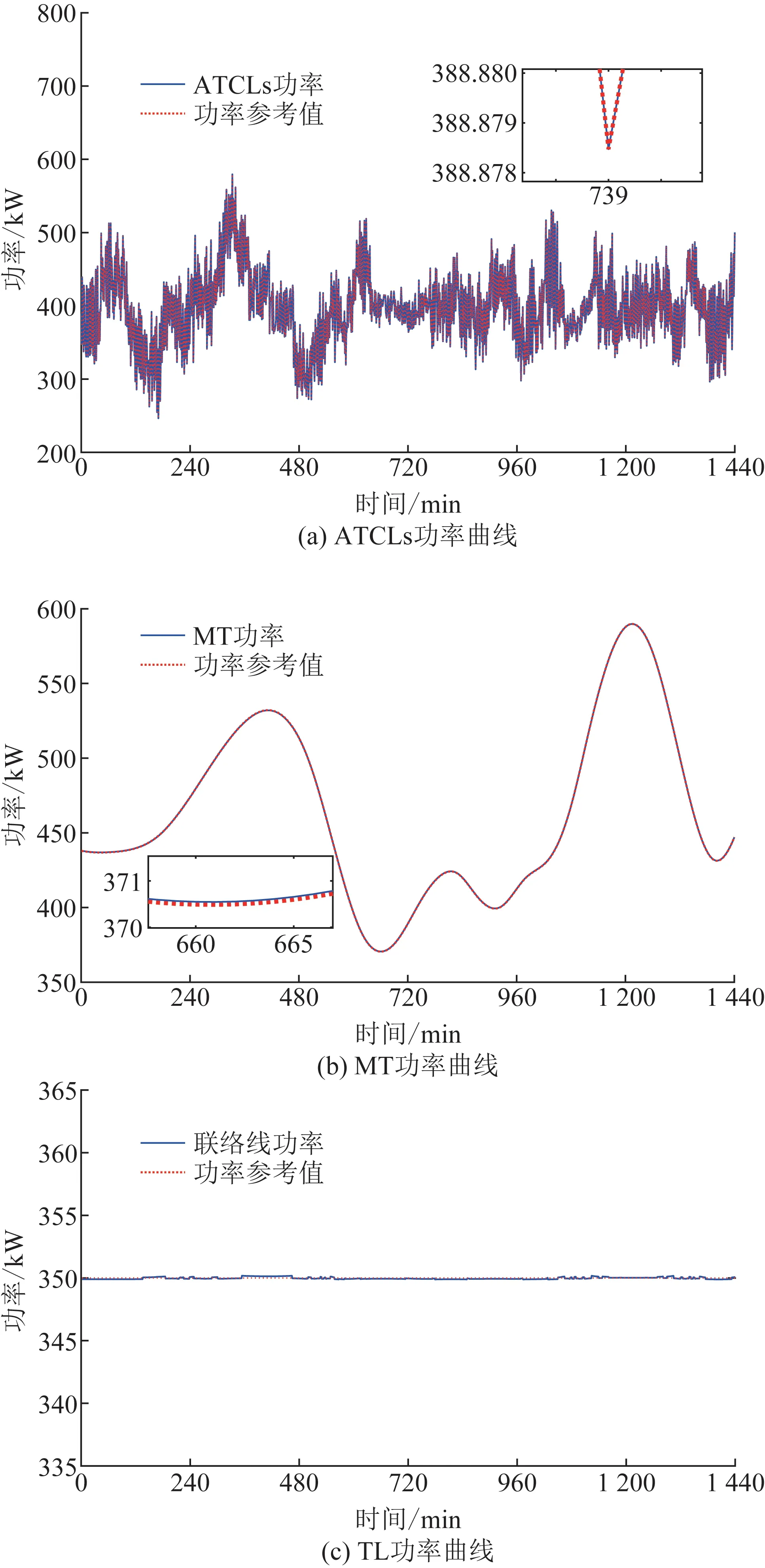
图8 联络线功率控制效果Fig.8 Tie-line power control performance

5 结 论

本文提出了采用ATCLs与MT共同抑制联络线功率波动的调控策略，在建立ATCLs双线性模型以及MT数学模型的基础上，设计了基于Lyapunov函数的改进MPC方法进行控制。仿真研究表明，提出的基于Lyapunov函数的改进MPC方法能够在满足温度舒适度约束下，使ATCLs输出功率有效跟踪高频参考值，并且求解时间相比传统MPC方法减少了约23%；能够在MT保持预设工作状态下，使其输出功率有效跟踪低频参考值，并且求解时间相比传统MPC方法缩短了约25%；最终较好实现了联络线功率波动平滑，仿真结果与理论分析保持了一致。但本文未对联络线功率参考值进行经济性优化，未来可研究计及经济性的联络线平滑策略。